Termodinámica

Magnitudes termodinámicas

El factor acéntrico se define como un parámetro necesario para calcular el factor de compresibilidad de un gas, éste mide la desviación en la presión de vapor de un compuesto, respecto a gases nobles como el criptón, xenón y argón (también llamados fluidos simples) para los cuales el factor acéntrico toma el valor de cero.

Definición

El factor acéntrico se define matemáticamente como¹

${\displaystyle \omega =-1-\log \left(P_{\mathrm {r} }^{\mathrm {sat} }(T_{\mathrm {r} }=0,7)\right)}$

donde

• ${\displaystyle \scriptstyle \omega }$ es el factor acéntrico;
• ${\displaystyle \scriptstyle T_{\mathrm {r} }={\frac {T}{T_{\mathrm {c} }}}}$ es la temperatura reducida;
• ${\displaystyle \scriptstyle T}$ es la temperatura;
• ${\displaystyle \scriptstyle T_{\mathrm {c} }}$ es la temperatura crítica;
• ${\displaystyle \scriptstyle P_{\mathrm {r} }^{\mathrm {sat} }={\frac {P^{\mathrm {sat} }}{P_{\mathrm {c} }}}}$ es la presión de vapor (o saturación) reducida;
• ${\displaystyle \scriptstyle P^{\mathrm {sat} }}$ es la es la presión de vapor del compuesto;
• ${\displaystyle \scriptstyle P_{\mathrm {c} }}$ es la presión crítica.

Es entonces que el factor acéntrico mide la no-esfericidad de la molécula cuando se trata de moléculas no polares, por ejemplo, hidrocarburos: un incremento en la longitud de la cadena (aumento de la no-esfericidad) produce un apartamiento en el valor de la presión reducida del compuesto. Como es lógico, este apartamiento es mínimo en el metano entre los hidrocarburos. El apartamiento también es pequeño para moléculas pequeñas y que son aproximadamente esféricas como oxígeno y nitrógeno moleculares.² Sin embargo, la definición abarca tanto compuestos polares como alcoholes, cetonas o incluso agua. En estos casos, la desviación en la presión de vapor se debe no sólo a la forma de la molécula, sino a las interacciones específicas entre ellas como dipolo-dipolo o puente de hidrógeno.

Usos

Cálculos de presión de vapor

El factor acéntrico puede ser utilizado para hacer cálculos aproximados de la presión de vapor. De la definición matemática se nota, que la presión de vapor reducida de un gas noble es aproximádamente 1, cuando la temperatura reducida es 0,7. Con esto se intuye que conociendo las propiedades críticas de un compuesto y su factor acéntrico, se tiene un punto de la curva de presión de vapor. Integrando la relación de Clausius-Clapeyron:

${\displaystyle {\frac {\mathrm {d} P^{\mathrm {sat} }}{\mathrm {d} T}}={\frac {\Delta H_{\mathrm {lv} }}{T\Delta V_{\mathrm {m} }}}}$

suponiendo que

• la entalpía de cambio de fase, ${\displaystyle \scriptstyle \Delta H_{\mathrm {lv} }}$, es constante;
• que el volúmen molar del líquido es mucho menor que el del vapor, haciendo que la variación entre los volúmenes de las fases ${\displaystyle \scriptstyle \Delta V_{\mathrm {m} }}$, sea aproximada mente igual al volumen molar del vapor, ${\displaystyle \scriptstyle V_{\mathrm {m,vap} }}$ y;
• que este vapor se comporta como un gas ideal: ${\displaystyle \scriptstyle V_{\mathrm {m,vap} }={\frac {RT}{P^{\mathrm {sat} }}}}$

se tiene

${\displaystyle {\frac {\mathrm {d} P^{\mathrm {sat} }}{P^{\mathrm {sat} }}}={\frac {\Delta H_{\mathrm {lv} }}{R}}{\frac {\mathrm {d} T}{T^{2}}}}$

e integrando entre una presión de referencia, ${\displaystyle \scriptstyle (T_{0},P_{0})}$, y una punto de la curva de presión de vapor cualquiera, ${\displaystyle \scriptstyle (T,P^{\mathrm {sat} })}$

${\displaystyle \ln \left({\frac {P^{\mathrm {sat} }}{P_{0}}}\right)={\frac {\Delta H_{\mathrm {lv} }}{R}}\left({\frac {1}{T}}-{\frac {1}{T_{0}}}\right)}$

Esta ecuación es fácilmente reescrita como una versión simplificada de la ecuación de Antoine. Si se toma el punto crítico como referencia, se intercambia logaritmo natural por decimal y se utiliza el valor del factor acéntrico para definir el punto ${\displaystyle \scriptstyle (0,7T_{\mathrm {c} },10^{-1-\omega }P_{\mathrm {c} })}$, el resultado final es³

${\displaystyle \log \left(P_{\mathrm {r} }^{\mathrm {sat} }\right)={\frac {7}{3}}(\omega +1)\left(1-{\frac {1}{T_{\mathrm {r} }}}\right)}$

Esta ecuación es muy buena para estimaciones rápidas de la presión de vapor. Sin embargo se debe entender que se trata de una aproximación. En general da buenos resultados arriba de ${\displaystyle \scriptstyle T_{\mathrm {c} }}$ = 0,5, pero el error puede incrementarse por debajo de los 2 bar.

El factor de compresibilidad (Z), conocido también como el factor de compresión, es la razón del volumen molar de un gas con relación al volumen molar de un gas ideal a la misma temperatura y presión. Es una propiedad termodinámica útil para modificar la ley de los gases ideales para ajustarse al comportamiento de un gas real.¹ En general, la desviación del comportamiento ideal se vuelve más significativa entre más cercano esté un gas a un cambio de fase, sea menor la temperatura o más grande la presión. Los valores de factor de compresibilidad son obtenidos usualmente mediante cálculos de las ecuaciones de estado, tales como la ecuación del virial la cual toma constantes empíricas de compuestos específicos como datos de entrada. Para un gas que sea una mezcla de dos o más gases puros (aire o gas natural, ejemplo), es requerida una composición del gas para que la compresibilidad sea calculada.

De manera alternativa, el factor de compresibilidad para gases específicos puede ser leída a partir de gráficos de compresibilidad generalizados¹ que grafiquen ${\displaystyle Z}$ como una función de la presión a temperatura constante.

Definición y significado físico

El factor de compresibilidad es definido como

${\displaystyle Z={\frac {V_{\mathrm {m} }}{(V_{\mathrm {m} })_{\text{gas ideal}}}}={\frac {pV_{\mathrm {m} }}{RT}},}$

donde ${\displaystyle V_{\mathrm {m} }}$ es el volumen molar, ${\displaystyle (V_{\mathrm {m} })_{\text{gas ideal}}=RT/p}$ es el volumen molar del correspondiente gas ideal, ${\displaystyle p}$ es la presión, ${\displaystyle T}$ es la temperatura, y ${\displaystyle R}$ es la constante universal de los gases ideales. Para aplicaciones de ingeniería, es expresado frecuentemente como

${\displaystyle Z={\frac {p}{\rho R_{\rm {specific}}T}},}$

donde ${\displaystyle \rho }$ es la densidad del gas y ${\displaystyle R_{\rm {specific}}=R/M}$ es la constante de los gases específica,² y ${\displaystyle M}$ es la masa molar.

Para un gas ideal, el factor de compresibilidad es ${\displaystyle Z=1}$ por definición. En muchas aplicaciones del mundo real, los requerimientos de precisión demandan que las desviaciones del comportamiento de un gas, esto es, el comportamiento de un gas real, sean tomadas en cuenta. El valor de ${\displaystyle Z}$ generalmente se incrementan con la presión y decrecen con la temperatura; a altas presiones las moléculas colisionan más a menudo, y esto permite que las fuerzas repulsivas entre las moléculas tengan un efecto notable, volviendo al volumen molar del gas real (${\displaystyle V_{\mathrm {m} }}$) más grande que el volumen molar del correspondiente gas ideal (${\displaystyle (V_{\mathrm {m} })_{\text{gas ideal}}=RT/p}$), lo que causa que ${\displaystyle Z}$ sea mayor a 1.³ Cuando las presiones son menores, las moléculas son libres de moverse; en este caso, dominan las fuerzas de atracción, haciendo que ${\displaystyle Z<1 annotation="">$. Cuanto más cercano esté el gas a su punto crítico o su punto de ebullición, ${\displaystyle Z}$ se desviará más del caso ideal.

Gráficas de factor de compresibilidad generalizados para gases puros

Diagrama generalizado del factor de compresibilidad.

La relación única entre el factor de compresibilidad y la temperatura y presión reducidas, ${\displaystyle T_{r}}$ y ${\displaystyle P_{r}}$ respectivamente, fue reconocida en principio por Johannes van der Waals en 1873 y es conocida como el teorema de los estados correspondientes de dos parámetros. El principio de estados correspondientes expresa la generalización de que las propiedades de un gas, las cuales dependen de las fuerzas moleculares, están relacionadas con las propiedades críticas del gas en una forma universal. Eso provee una base más importante para desarrollar correlaciones de propiedades moleculares.

En cuanto a la compresibilidad de los gases, el principio de estados correspondientes indica que cualquier gas puro a la misma temperatura reducida, ${\displaystyle T_{r}}$, y presión reducida, ${\displaystyle P_{r}}$, debe tener el mismo factor de compresibilidad.

La temperatura y la presión reducidas están definidas por

${\displaystyle T_{r}={\frac {T}{T_{c}}}}$ y ${\displaystyle P_{r}={\frac {P}{P_{c}}}.}$

Aquí ${\displaystyle T_{c}}$ y ${\displaystyle P_{c}}$ son la temperatura crítica y la presión crítica del gas, respectivamente. Estas son características de cada gas específico, siendo ${\displaystyle T_{c}}$ la temperatura sobre la cual no es posible licuar un gas dado y ${\displaystyle P_{c}}$ es la presión mínima requerida para licuar un gas en su temperatura crítica. Juntos ellos definen el punto crítico de un fluido sobre el cual no existe una distinción entre las fases líquida y gaseosa de un fluido dado.

Los datos de presión-volumen-temperatura (PVT) para gases reales varían de un gas puro a otro. Sin embargo, cuando los factores de compresibilidad de varios gases de un solo componente se grafican en contra de la presión junto con isotermas de temperatura, muchos de los gráficos exhiben similares formas de isotermas.

Para obtener un gráfico generalizado que pueda ser usado para muchos diferentes gases, la presión y temperatura reducidas, ${\displaystyle P_{r}}$ y ${\displaystyle T_{r}}$, se utilizan para normalizar los datos del factor de compresibilidad. La figura mostrada es un ejemplo de un gráfico de factor de compresibilidad generalizado derivado de cientos de datos experimentales PVT de 10 gases puros, que fueron metano, etano, eteno, propano, n-butano, i-pentano, n-hexano, nitrógeno, dióxido de carbono y vapor.

Existen gráficos de factor de compresibilidad generalizados más detallados basados en tantos como 25 o más gases puros diferentes, tales como los gráficos Nelson-Obert graphs. Dichos gráficos se dice que tienen una precisión dentro del 1-2 por ciento para valores de ${\displaystyle Z}$ mayores que 0.6 y dentro del 4-6 por ciento para valores de ${\displaystyle Z}$ entre 0.3-0.6.

Los gráficos de factor de compresibilidad generalizados pueden ser considerablemente erróneos para gases fuertemente polares, los cuales son gases para los que los centros de carga positiva y negativa no coinciden. En tales casos, el estimado de ${\displaystyle Z}$ puede ser erróneo por tanto como 15-20 por ciento.

Los gases cuánticos hidrógeno, helio y neón no se ajustan al comportamiento de estados correspondientes y la presión y temperatura reducidas para esos tres gases deberían ser redefinidas de la siguiente forma para mejorar la precisión al predecir sus factores de compresibilidad cuando se utilizan los gráficos generalizados:

${\displaystyle T_{r}={\frac {T}{T_{c}+8}}}$ y ${\displaystyle P_{r}={\frac {P}{P_{c}+8}}}$

donde las temperaturas están en kelvin y las presiones en atmósferas.⁴

Modelos teóricos

La ecuación del virial es especialmente útil para describir las causas de la no-idealidad a nivel molecular (muy pocos gases son monoatómicos) ya que se deriva directamente de la mecánica estadística:

${\displaystyle {\frac {PV_{\mathrm {m} }}{RT}}=1+{\frac {B}{V_{\mathrm {m} }}}+{\frac {C}{V_{\mathrm {m} }^{2}}}+{\frac {D}{V_{\mathrm {m} }^{3}}}+\dots }$

donde los coeficientes en el numerador se conocen como coeficientes viriales y son funciones de la temperatura.

Los coeficientes viriales tienen en cuenta las interacciones entre grupos sucesivamente más grandes de moléculas. Por ejemplo, ${\displaystyle B}$ toma en cuenta interacciones entre pares, ${\displaystyle C}$ toma en cuenta interacciones entre tres moléculas de gas, y así sucesivamente. Debido a que las interacciones entre grandes números de moléculas son raros, la ecuación del virial es usualmente truncada después del tercer término.⁵

Valores experimentales

Es extremadamente difícil generalizar a qué valores de presión o temperatura se vuelve importante la desviación del comportamiento de gas ideal. Como regla general, la ley de los gases ideales es razonablemente precisa hasta una presión de alrededor de 2 atmósferas, e incluso mayor para moléculas pequeñas no asociantes. Por ejemplo para el clorometano, una molécula altamente polar y por tanto con fuerzas intermoleculares significativas, el valor experimental para el factor de compresibilidad es de ${\displaystyle Z=0.9152}$ a una presión de 10 atm y una temperatura de 100 °C.⁶ Para el aire (pequeñas moléculas no polares) en aproximadamente las mismas condiciones, el factor de compresibilidad es de solo ${\displaystyle Z=1.0025}$ (véase la tabla debajo para 10 bars, 400 K).

Compresibilidad del aire

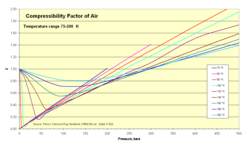
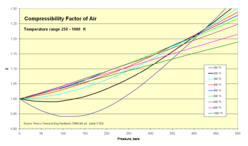
El aire normal se comprende en números crudos de alrededor de 80 por ciento de nitrógeno N² y 20 por ciento de oxígeno O². Ambas moléculas son pequeñas y no polares (y por tanto, no asociantes). Se puede por tanto esperar que el comportamiento del aire dentro de rangos amplios de temperatura y presión pueda ser aproximado con razonable precisión como el de un gas ideal. Los valores experimentales para el factor de compresibilidad confirman esto.

• Z para el aire como función de la presión 1-500 bar
• 

  Isotermas a 75-200 K
 
• 

  Isotermas a 250-1000 K

Factor de compresibilidad para el aire (valores experimentales)

	Presión, bar (absoluta)
Temp, K	1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0.0052	0.0260	0.0519	0.1036	0.2063	0.3082	0.4094	0.5099	0.7581	1.0125
80		0.0250	0.0499	0.0995	0.1981	0.2958	0.3927	0.4887	0.7258	0.9588	1.1931	1.4139
90	0.9764	0.0236	0.0453	0.0940	0.1866	0.2781	0.3686	0.4681	0.6779	0.8929	1.1098	1.3110	1.7161	2.1105
100	0.9797	0.8872	0.0453	0.0900	0.1782	0.2635	0.3498	0.4337	0.6386	0.8377	1.0395	1.2227	1.5937	1.9536
120	0.9880	0.9373	0.8860	0.6730	0.1778	0.2557	0.3371	0.4132	0.5964	0.7720	0.9530	1.1076	1.5091	1.7366
140	0.9927	0.9614	0.9205	0.8297	0.5856	0.3313	0.3737	0.4340	0.5909	0.7699	0.9114	1.0393	1.3202	1.5903
160	0.9951	0.9748	0.9489	0.8954	0.7803	0.6603	0.5696	0.5489	0.6340	0.7564	0.8840	1.0105	1.2585	1.4970
180	0.9967	0.9832	0.9660	0.9314	0.8625	0.7977	0.7432	0.7084	0.7180	0.7986	0.9000	1.0068	1.2232	1.4361
200	0.9978	0.9886	0.9767	0.9539	0.9100	0.8701	0.8374	0.8142	0.8061	0.8549	0.9311	1.0185	1.2054	1.3944
250	0.9992	0.9957	0.9911	0.9822	0.9671	0.9549	0.9463	0.9411	0.9450	0.9713	1.0152	1.0702	1.1990	1.3392
300	0.9999	0.9987	0.9974	0.9950	0.9917	0.9901	0.9903	0.9930	1.0074	1.0326	1.0669	1.1089	1.2073	1.3163
350	1.0000	1.0002	1.0004	1.0014	1.0038	1.0075	1.0121	1.0183	1.0377	1.0635	1.0947	1.1303	1.2116	1.3015
400	1.0002	1.0012	1.0025	1.0046	1.0100	1.0159	1.0229	1.0312	1.0533	1.0795	1.1087	1.1411	1.2117	1.2890
450	1.0003	1.0016	1.0034	1.0063	1.0133	1.0210	1.0287	1.0374	1.0614	1.0913	1.1183	1.1463	1.2090	1.2778
500	1.0003	1.0020	1.0034	1.0074	1.0151	1.0234	1.0323	1.0410	1.0650	1.0913	1.1183	1.1463	1.2051	1.2667
600	1.0004	1.0022	1.0039	1.0081	1.0164	1.0253	1.0340	1.0434	1.0678	1.0920	1.1172	1.1427	1.1947	1.2475
800	1.0004	1.0020	1.0038	1.0077	1.0157	1.0240	1.0321	1.0408	1.0621	1.0844	1.1061	1.1283	1.1720	1.2150
1000	1.0004	1.0018	1.0037	1.0068	1.0142	1.0215	1.0290	1.0365	1.0556	1.0744	1.0948	1.1131	1.1515	1.1889

Fuente: Perry's chemical engineers' handbook (6a edición). MCGraw-Hill. 1984. ISBN 0-07-049479-7. (tabla 3-162). Los valores de ${\displaystyle Z}$ son calculados a partir de valores de presión, volumen (o densidad), y temperatura en Vassernan, Kazavchinskii, y Rabinovich, Thermophysical Properties of Air and Air Components; Moscú, Naúka, 1966, y NBS-NSF Trans. TT 70-50095, 1971: y Vassernan y Rabinovich, Thermophysical Properties of Liquid Air and Its Component, Moscú, 1968, y NBS-NSF Trans. 69-55092, 1970.