Termodinámica

Ecuaciones de la termodinámica

Las Relaciones de Maxwell son un conjunto de ecuaciones termodinámicas que se derivan del Teorema de Clairaut, también conocido como teorema de Schwarz o teorema de la igualdad de las derivadas cruzadas o segundas derivadas y de las definiciones de los potenciales termodinámicos (ecuación constitutiva asociada a un sistema termodinámico que tiene dimensiones de energía potencial). Estas relaciones se denominan así por el físico del siglo XIX James Clerk Maxwell.

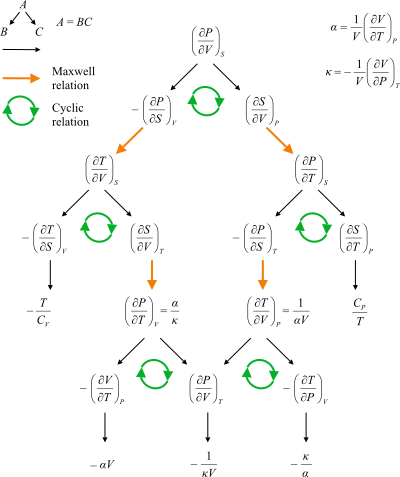
Diagrama de flujo que muestra los caminos entre las relaciones de Maxwell. P: presión, T: temperatura, V: volumen, S: entropía, α: coeficiente de expansión térmica, κ: compresibilidad, C_V: capacidad calorífica a volumen constante, C_P: capacidad calorífica a presión constante.

La estructura de las relaciones de Maxwell es una declaración de igualdad entre las segundas derivadas para funciones continuas. A partir del hecho que el orden de diferenciación de una función analítica de dos variables es irrelevante (Schwarz teorema). En el caso de relaciones de Maxwell la función a considerar es un potencial termodinámico xi y xj es dos variables naturales diferentes para ese potencial:

Teorema' Schwarz (general) ${\displaystyle {\frac {\partial }{\partial x_{j}}}\left({\frac {\partial \Phi }{\partial x_{i}}}\right)={\frac {\partial }{\partial x_{i}}}\left({\frac {\partial \Phi }{\partial x_{j}}}\right)}$

donde las derivadas parciales con respecto a las dos variables naturales, se vuelven a derivar parcialmente con respecto a la variable contraria respectivamente. Entonces podemos decir que para cada potencial termodinámico (ecuación que relaciona las variables termodinámicas) hay n(n − 1)/2 posibles relaciones de Maxwell donde n es el número de variables naturales para ese potencial.

Las cuatro relaciones más comunes de Maxwell

Las cuatro relaciones de Maxwell más comunes son las igualdades de las segundas derivadas, de cada uno de los cuatro potenciales termodinámicos, con respecto a sus variables naturales térmicas (temperatura T; o entropía S) y sus variables naturales mecánicas (presiónP; o volumen V):

Relaciones de Maxwell (comunes) ${\displaystyle {\begin{aligned}+\left({\frac {\partial T}{\partial V}}\right)_{S}&=&-\left({\frac {\partial P}{\partial S}}\right)_{V}&=&{\frac {\partial ^{2}U}{\partial S\partial V}}\\+\left({\frac {\partial T}{\partial P}}\right)_{S}&=&+\left({\frac {\partial V}{\partial S}}\right)_{P}&=&{\frac {\partial ^{2}H}{\partial S\partial P}}\\+\left({\frac {\partial S}{\partial V}}\right)_{T}&=&+\left({\frac {\partial P}{\partial T}}\right)_{V}&=&-{\frac {\partial ^{2}F}{\partial T\partial V}}\\-\left({\frac {\partial S}{\partial P}}\right)_{T}&=&+\left({\frac {\partial V}{\partial T}}\right)_{P}&=&{\frac {\partial ^{2}G}{\partial T\partial P}}\end{aligned}}\,\!}$

El cuadro termodinámico con potenciales resaltados en rojo

donde los potenciales como funciones de sus variables naturales térmicas y mecánicas son la energía interna U(S, V), entalpía H(S, P), energía libre de Helmholtz F(T, V) and energía libre de Gibbs G(T, P). Como auxiliar, podemos recurrir al cuadro termodinámico o rueda termodinámica, que es el diagrama de Max Born, que se utiliza para ayudar a determinar las relaciones termodinámicas. La utilidad de estas relaciones se encuentra en cuantificar los cambios de entropía, que no son medibles directamente, en términos de cantidades medibles como la temperatura, el volumen y la presión.

Derivación

Las relaciones de Maxwell se basan en las reglas de derivadas parciales simples, en particular, el diferencial total de una función y la  igualdad de la evaluación de derivadas parciales de segundo orden.

[mostrar]Derivación

[mostrar]Derivación extendida

Relaciones generales de Maxwell 

Lo anterior expuesto no son las únicas relaciones de Maxwell. Cuando se consideran otros términos de trabajo que implican otras variables naturales, además del trabajo de volumen o cuando el número de partículas se incluye como una variable natural, otras relaciones de Maxwell se hacen evidentes. 

Por ejemplo, si tenemos un gas de un solo componente, entonces el número de partículas N es también una variable natural de los cuatro anteriores potenciales termodinámicos. La relación de Maxwell para la entalpía con respecto a la presión y al número de partículas sería entonces:

${\displaystyle \left({\frac {\partial \mu }{\partial P}}\right)_{S,N}=\left({\frac {\partial V}{\partial N}}\right)_{S,P}\qquad ={\frac {\partial ^{2}H}{\partial P\partial N}}}$

donde μ es el potencial químico. Además, hay otros potenciales termodinámicos además de los cuatro que se utilizan comúnmente, y cada uno de estos potenciales rendirán un conjunto de relaciones de Maxwell.

Cada ecuación puede ser re-expresa utilizando la relación:

${\displaystyle \left({\frac {\partial y}{\partial x}}\right)_{z}=1\left/\left({\frac {\partial x}{\partial y}}\right)_{z}\right.}$

los cuales son a veces también conocidos como relaciones de Maxwell.

Las ecuaciones que relacionan las derivadas parciales de las propiedades , ,  y  de un sistema compresible simple entre sí se conocen como relaciones de Maxwell. Se obtienen a partir de las cuatro ecuaciones de Gibbs explotando la exactitud de las diferenciales de las propiedades termodinámicas.

De las relaciones de Gibbs se tiene

(10)

(11)

Las otras relaciones de Gibss se basan en dos nuevas combinaciones de propiedades: la función del Helmholtz  y la función de Gibbs  definidas como:

(12)

(13)

Al diferenciar se obtiene

Si se simplifican las relaciones anteriores con las ecuaciones () y () se obtienen las otras relaciones de Gibbs para sistemas compresibles simples.

(14)

(15)

Un examen cuidadoso de las cuatro relaciones de Gibbs muestra que tienen la forma de la ecuación

con

puesto que  y  son propiedades y en consecuencia, tienen diferenciales exactas. De tal suerte que podemos escribir:

(16)

(17)

(18)

(19)

Éstas se llaman las relaciones de Maxwell. Son de gran valor en la termodinámica por que brindan un medio para determinar el cambio de entalpía que no es posible medir directamente, a partir de la medición de los cambios en las propiedades ,  y . Note que las relaciones de Maxwell presentadas se limitan a sistemas compresibles simples. Sin embargo, otras relaciones similares se describen con la misma facilidad para sistemas no simples como los que incluyen efectos electrolíticos, magnéticos y otro tipo.

 ecuación de Clausius-Clapeyron es una manera de caracterizar una transición de fase de primer orden que tiene lugar en un sistema monocomponente. En un diagrama P-T (presión-temperatura), la línea que separa ambos estados se conoce como curva de coexistencia. La relación de Clausius-Clapeyron determina la pendiente de dicha curva. Matemáticamente se puede expresar como:

${\displaystyle {\frac {dP}{dT}}={\frac {\Delta {H}}{T\Delta V}}}$

donde ${\displaystyle {\frac {dP}{dT}}}$ es la pendiente de dicha curva, ${\displaystyle \Delta {H}}$ es el calor latente o entalpía del cambio de fase y ${\displaystyle \Delta V}$ es el volumen.

Derivación

Supónganse dos fases, ${\displaystyle \alpha }$ y ${\displaystyle \beta }$, en contacto y en equilibrio ambas. Los potenciales químicos se relacionan según ${\displaystyle \mu _{\alpha }=\mu _{\beta }}$. A lo largo de la curva de coexistencia, se tiene que ${\displaystyle d\mu _{\alpha }=d\mu _{\beta }}$. Usando la relación de Gibbs-Duhem ${\displaystyle d\mu =-sdT+vdP}$ donde s y v son, respectivamente, la entropía y el volumen por partícula, se obtiene:

${\displaystyle (s_{\beta }-s_{\alpha })dT+(v_{\alpha }-v_{\beta })dP=0}$

Reordenando la expresión se tiene:

${\displaystyle {\frac {dP}{dT}}={\frac {s_{\beta }-s_{\alpha }}{v_{\beta }-v_{\alpha }}}}$

De la relación entre el cambio de calor y entropía en un proceso reversible ${\displaystyle \delta Q=TdS}$, se tiene que la cantidad de calor añadido en la reacción es:

${\displaystyle \delta H=T(s_{\beta }-s_{\alpha })}$

y combinando las dos últimas ecuaciones se obtiene la relación estándar.

Aplicación

Esta expresión puede ser usada para predecir dónde se va a dar una transición de fase. Por ejemplo, la relación de Clausius-Clapeyron se usa frecuentemente para explicar el patinaje sobre hielo: el patinador (de unos 70 kg), con la presión de sus cuchillas, aumenta puntualmente la presión sobre el hielo, lo cual lleva a éste a fundirse. ¿Funciona dicha explicación? Si T=−2 °C, se puede emplear la ecuación de Clausius-Clapeyron para hallar la presión necesaria para fundir el hielo a dicha temperatura. Asumiendo que la variación de la temperatura es pequeña, y que por tanto se puede considerar constante tanto el calor latente de fusión como los volúmenes específicos, se puede usar:

${\displaystyle {\Delta P}={\frac {L}{T\Delta V}}{\Delta T}}$

y sustituyendo los valores de:

L = 3,34·10⁵ J/kg,

T=271,15 K,

${\displaystyle \Delta V}$ = -9,05·10^-5 m³/kg, y

${\displaystyle \Delta T}$ = 2 K

se obtiene:

${\displaystyle \Delta P}$ = 27,2 MPa = 277,36 kgf/cm²

Esta presión es la equivalente a la de un peso de 150 kg (luchador de sumo) situado sobre unos patines de área total de contacto con el hielo de 0,54 cm². Evidentemente, éste no es el mecanismo por el cual se funde el hielo bajo las cuchillas de los patines (es un efecto de calentamiento por fricción).

Características de la ecuación de Clausius-Clapeyron.

• La condensación tiende a volver el gas que se ha formado por vaporización al estado líquido.

• La velocidad de condensación aumenta a medida que tiene lugar la vaporización, y aumenta la presión del vapor.

• El valor de la presión de vapor es independiente de las cantidades del líquido y vapor, mientras haya presente cualquier superficie libre del líquido. Este valor depende en realidad de la cantidad de moléculas ganadas o perdidas por el líquido.

• A mayor área expuesta al vapor, mayor será la cantidad de moléculas ganadas por el líquido.

• La composición del líquido es determinante en el valor de la presión de vapor durante el equilibrio.

• A mayor masa molecular menor valor en la presión de vapor. Este tipo de tratamiento permite además obtener los valores del calor y de la entropía de vaporización del líquido. Existen varios métodos para medir la presión de vapor. Los más conocidos son:

• El isoteniscopio, cuando la presión externa es igual a la presión de vapor el manómetro de comparación, sumergido en el baño, debe tener la misma altura en las dos ramas. (Al igual que la guía en el paso 4.3.3)

• El aparato de Ramsey - Yung, el depósito del termómetro esta a la temperatura del líquido que se halla en equilibrio con la presión a que está sometido el sistema. dlnP/dT= H vap dT/ RT2 Esta es la ecuación de Clausius-Clapeyron la cual al integrarla, se obtiene: lnP=- H vap/ RT + C

Cuando representamos gráficamente lnP vs 1/T, se obtiene una recta con pendiente igual a - H vap/ R y ordenada en el origen igual a C. La presión de vapor del líquido de una sustancia pura, a diferentes temperaturas cumple esta ecuación de Clausius, esto es lo que se pretende constatar con la práctica del laboratorio #2. Para una substancia pura existe una relación definida entre la presión de saturación y la temperatura de saturación, la cual puede ser representada mediante una curva típica como se muestra en la figura1, la cual recibe el nombre de curva de presión de vapor. El término temperatura de saturación designa la temperatura en la cual se efectúa la vaporización a una presión dada, y esta presión recibe el nombre de presión de saturación para la temperatura dada. Como se puede observar en la gráfica, la curva de presión del vapor va creciendo a medida que aumenta la temperatura y la presión. Cuando existe alguna substancia, una parte en forma líquida y otra como vapor a la temperatura de saturación, se define su calidad como la proporción de la masa de vapor a la masa total. O sea: si la masa del vapor es 0.2 kg y la masa del líquido es 0.8 kg, la calidad es del 20 %. Ésta puede considerarse como una propiedad intensiva y tiene el símbolo X. La palabra calidad solo tiene sentido cuando las substancias se hallan en un estado saturado; esto es, a presión y temperatura de saturación. Igualmente la calidad del vapor puede ser determinado mediante la siguiente ecuación: Calidad = x = mv/ mv +ml (mv = msa de vapor, ml = msa del líquido)

Importancia de la ecuación de Clausius-Capleyron. Ésta es una importante relación termodinámica pues permite determinar la entalpía de vaporización a una temperatura determinada midiendo simplemente la pendiente de la curva de saturación en un diagrama P-T y el volumen específico del líquido saturado y el vapor saturado a la temperatura dada. La ecuación de Clapeyron permite calcular la pendiente de una línea de equilibrio entre dos fases en el diagrama de fases P-T de un sistema de un componente.