| Parte de una serie en |
| Cosmologia fisica |
|---|
 |
El Big Crunch es uno de los escenarios teóricos para el destino final del universo , en el que la expansión métrica del espacio se invierte y el universo retrocede, haciendo que el factor de escala cósmica llegue a cero o causando una reforma del universo comenzando con otro. Big Bang .
La evidencia experimental reciente sugiere que la expansión del universo no se está frenando por la gravedad, sino que se está acelerando . Sin embargo, debido a que la naturaleza de la energía oscura que se postula para impulsar la aceleración es desconocida, un Big Crunch todavía es posible, aunque no está respaldado por observaciones a partir de hoy. [ cita requerida ]
Descripción general [ editar ]
Si la velocidad de expansión del universo no excede la velocidad de escape , la atracción gravitatoria mutua de toda su materiaeventualmente causará que se contraiga. Si la entropía continúa aumentando en la fase de contratación (ver hipótesis Ergódica ), la contracción parecería muy diferente de la inversión temporal de la expansión. Mientras que el universo primitivo era altamente uniforme, un universo en contracción se volvería cada vez más agrupado. [1] Finalmente, toda la materia se colapsaría en agujeros negros , que luego se unirían, produciendo un agujero negro unificado o singularidad Big Crunch.
La idea detrás de la teoría es que la expansión del universo está vinculada a la energía liberada en el Big Bang , por lo tanto, la velocidad de la materia disminuiría con el tiempo debido a la gravedad (atracción mutua). Esto actuaría como lastre y, eventualmente, conduciría a un alto de la expansión. A medida que la materia atrae y no hay materia más allá del punto de expansión máximo, eventualmente toda la materia comenzará a viajar hacia el interior nuevamente, acelerándose a medida que pasa el tiempo.
Los detalles exactos de los eventos que tendrían lugar antes de dicho colapso final dependen de la duración de la fase de expansión y de la fase de contracción previa; cuanto más duraran los dos, más eventos esperados tendrían lugar en un universo en constante expansión ; sin embargo, se espera que la fase de contracción no sea notada inmediatamente por observadores hipotéticos debido al retraso causado por la velocidad de la luz , que la temperatura del fondo cósmico de microondas aumente simétricamente durante la contracción en comparación con la fase de expansión anterior, y que los eventos que tuvo lugar durante el Big Bang ocurriría en orden opuesto. [2]Para un Universo en contratación similar al nuestro en su composición, se espera que los supercúmulos se fusionen entre sí, seguidos por cúmulos de galaxias y galaxias posteriores. Para cuando las estrellas estuvieran tan cerca que las colisiones entre ellas fueran frecuentes, la temperatura del microondas cósmico de fondo habría aumentado tanto que las estrellas no podrían expulsar su calor interno, cocinando lentamente hasta que explotaron, dejando atrás un calor caliente. gas heterogéneo, cuyos átomos se descompondrían en sus partículas subatómicas constituyentes debido al aumento de la temperatura, que serían absorbidos por los agujeros negros ya coalescentes antes del Big Crunch. [2]
La constante de Hubble mide el estado actual de expansión en el universo, y la fuerza de la fuerza gravitacional depende de la densidad y la presión de la materia en el universo, o en otras palabras, la densidad crítica del universo. Si la densidad del universo es mayor que la densidad crítica, entonces la fuerza de la fuerza gravitatoria detendrá la expansión del universo y el universo colapsará sobre sí mismo [1], asumiendo que no hay fuerza repulsiva como una constante cosmológica. A la inversa, si la densidad del universo es menor que la densidad crítica, el universo continuará expandiéndose y la atracción gravitatoria no será suficiente para detener la expansión del universo. Este escenario resultaría en la muerte térmica del universo , donde el universo alcanza el estado máximo de entropía que es el equilibrio termodinámico . En el estado de equilibrio termodinámico, la energía en el universo se distribuye de manera uniforme, por lo que la transferencia de calor o cualquier otra transferencia de energía es imposible, por lo que no pueden producirse reacciones en ese universo que lo hace "muerto". [3] [ no en la cita dada ]Una teoría propone que el universo podría colapsar al estado en el que comenzó y luego iniciar otro Big Bang , [1] por lo tanto, el universo duraría para siempre, pero atravesaría las fases de expansión (Big Bang) y contracción (Big Crunch). ). [4] Otro escenario da como resultado un universo plano que se produce cuando la densidad crítica es la correcta. En este estado, el universo siempre se ralentizaría y, eventualmente, se detendría en un tiempo interminable. Aunque ahora se entiende que la densidad crítica se ha medido y determinado como un universo plano. [5]
La evidencia experimental a fines de los años 90 y principios de los 2000 (a saber, la observación de supernovasdistantes como velas estándar y el mapeo bien resuelto del fondo cósmico de microondas ) [6] [7] llevó a la conclusión de que la expansión del universo no es siendo disminuido por la gravedad, pero más bien acelerando. Sin embargo, investigaciones más recientes, basadas en conjuntos de datos más grandes, han puesto en duda esta conclusión [8] .
En la cosmología física , el Big Rip es un hipotético modelo cosmológico relacionado con el destino final del universo , en el que la materia del universo , desde las estrellas y galaxias hasta los átomos y las partículas subatómicas, e incluso el propio espacio-tiempo , se desgarra progresivamente por la expansión. del universo en un determinado momento en el futuro. Según la hipótesis, publicada por primera vez en 2003, el factor de escala del universo y con ello todas las distancias en el universo, que se sabe que se está acelerando., se encontrará que aumenta exponencialmente. Si esto sucediera, el modelo especula que con el tiempo, en muchos miles de millones de años, el factor de escala se volvería infinitamente grande, separando incluso las partículas subatómicas y el tejido del espacio-tiempo , terminando nuestro universo. [ cita requerida ]
La posibilidad de singularidades repentinas y singularidades decontracción o rasgadura se produce solo para materia hipotética con propiedades físicas inverosímiles.
Descripción general [ editar ]
La hipótesis se basa fundamentalmente en el tipo de energía oscura en el universo . El tipo que podría causar esta hipótesis es una forma constantemente creciente de energía oscura. Si la energía oscura en el universo aumenta sin límite, podría superar todas las fuerzas que mantienen unido al universo. El valor clave [ ¿por qué? ] es la ecuación del parámetro de estado w , la relación entre la presión de energía oscura y su densidad de energía . Si w <−1, esta energía dinámica de vacío se conoce como energía fantasma , un extremo [ ¿cómo? ] forma de quintaesencia.
Expansión [ editar ]
Un universo dominado por la energía fantasma es un universo acelerado , que se expande a un ritmo cada vez mayor. Sin embargo, esto implica que el tamaño del universo observable se está reduciendo continuamente; La distancia al borde del universo observable que se aleja a la velocidad de la luz desde cualquier punto se acerca cada vez más. Cuando el tamaño del universo observable se vuelve más pequeño que cualquier estructura particular, ninguna interacción de ninguna de las fuerzas fundamentales puede ocurrir entre las partes más remotas de la estructura. Cuando estas interacciones se vuelven imposibles, la estructura se "desgarra". El modelo implica que después de un tiempo finito habrá una singularidad final, llamada "Big Rip", en la que todas las distancias divergirán a valores infinitos.
Los autores de esta hipótesis, liderados por Robert R. Caldwell de Dartmouth College , calculan el tiempo desde el presente hasta el final del universo tal como lo conocemos para que esta forma de energía sea
donde w se define arriba, H 0 es la constante de Hubble y Ω m es el valor presente de la densidad de toda la materia en el universo.
Ejemplo de autores [ editar ]
En su artículo, los autores consideran un ejemplo hipotético con w = −1.5, H 0 = 70 km / s / Mpc y Ω m = 0.3, en cuyo caso el Big Rip ocurrirá aproximadamente 22 mil millones de años a partir del presente.
Para w = −1.5, las galaxias primero se separarán unas de otras. Aproximadamente 60 millones de años antes del Big Rip, la gravedad sería demasiado débil para mantener a la Vía Láctea y otras galaxias individuales juntas. Las galaxias serían destruidas como estrellas separadas del agujero negro principal. Aproximadamente tres meses antes de Big Rip, el Sistema Solar (o sistemas similares a los nuestros en este momento, ya que el destino del Sistema Solar 22 mil millones de años en el futuro es cuestionable) sería gravitacional sin consolidar. Los planetas serían separados de la órbita de la estrella. En los últimos minutos, las estrellas y los planetas se desgarrarían, y en un período de tiempo extremadamente corto antes del Big Rip, los átomossería destruido. En el momento en que se produce el Big Rip, incluso el propio espacio-tiempo se desgarrará y el factor de escala será infinito. [2]
Universo observado [ editar ]
La evidencia indica que w está muy cerca de −1 en nuestro universo, lo que hace que w sea el término dominante en la ecuación. Cuanto más cerca esté w de −1, más cercano estará el denominador a cero y más lejos estará Big Rip en el futuro. Si w fuera exactamente igual a −1, el Big Rip no podría ocurrir, independientemente de los valores de H 0 o Ω m .
Según los últimos datos cosmológicos disponibles, las incertidumbres son todavía demasiado grandes para discriminar entre los tres casos w <−1, w = −1, y w > −1.
| Parte de una serie en |
| Cosmologia fisica |
|---|
 |
Universo temprano
|
Expansión · Futuro
|
Componentes · Estructura
|
| La relatividad general delWikilibro tiene una página sobre el tema de: BKL singularidad |
Una singularidad Belinskii - Khalatnikov - Lifshitz (BKL)es un modelo de la evolución dinámica del Universo cerca de la singularidad inicial , descrita por una solución anisotrópica y caótica de las ecuaciones de campo de Einstein de la gravitación. [1] Según este modelo, el Universo está oscilando caóticamente alrededor de una singularidad gravitatoria en la que el tiempo y el espacio se vuelven iguales a cero. Esta singularidad es físicamente real en el sentido de que es una propiedad necesaria de la solución y aparecerá también en la solución exacta.de esas ecuaciones. La singularidad no se crea artificialmente por las suposiciones y simplificaciones hechas por las otras soluciones especiales , como las soluciones de Friedmann-Lemaître-Robertson-Walker , cuasi-isotrópica y Kasner .
La imagen desarrollada por BKL tiene varios elementos importantes. Estos son:
- Cerca de la singularidad, la evolución de la geometría en diferentes puntos espaciales se desacopla de modo que las soluciones de las ecuaciones diferenciales parcialesse puedan aproximar mediante soluciones de ecuaciones diferenciales ordinarias con respecto al tiempo para los factores de escala espacial adecuadamente definidos. Esto se llama la conjetura BKL .
- Para la mayoría de los tipos de materia, el efecto de los campos de materia en la dinámica de la geometría se vuelve insignificante cerca de la singularidad. O, en palabras de John Wheeler , "la materia no importa" cerca de una singularidad. El trabajo BKL original planteó un efecto insignificante para toda la materia, pero luego teorizaron que la "materia rígida" (ecuación de estado p = ε) equivalente a un campo escalar sin masa puede tener un efecto modificador en la dinámica cercana a la singularidad.
- Las ecuaciones diferenciales ordinarias que describen los asintóticos son aquellas que provienen de una clase de soluciones espacialmente homogéneas que constituyen la dinámica de Mixmaster : un modelo oscilatorio y caótico complicado que exhibe propiedades similares a las discutidas por BKL.
El estudio de la dinámica del universo en la vecindad de la singularidad cosmológica se ha convertido en un campo en rápido desarrollo de la física teórica y matemática moderna. La generalización del modelo BKL a la singularidad cosmológica en modelos cosmológicos multidimensionales (tipo Kaluza-Klein ) tiene un carácter caótico en los tiempos espaciales cuya dimensionalidad no es superior a diez, mientras que en los espacios espaciales de dimensiones más altas, un universo después de experimentar un número finito de Las oscilaciones entran en un régimen de contratación tipo Kasner monotónico. [2] [3] [4]
El desarrollo de estudios cosmológicos basados en modelos de supercuerdas ha revelado algunos aspectos nuevos de la dinámica en la vecindad de la singularidad. [5] [6] [7] En estos modelos, los mecanismos de cambio de las épocas de Kasner son provocados no por las interacciones gravitacionales sino por la influencia de otros campos presentes. Se demostró que los modelos cosmológicos basados en seis modelos de supercuerdas principales más el modelo de supergravedad D = 11 exhiben la dinámica caótica de BKL hacia la singularidad. Se descubrió una conexión entre los modelos cosmológicos tipo BKL oscilatorios y una subclase especial de álgebras de Lie de dimensión infinita , las llamadas álgebras Kac-Moody hiperbólicas .
Introducción [ editar ]
La base de la cosmología moderna son las soluciones especiales de las ecuaciones de campo de Einsteinencontradas por Alexander Friedmann en 1922–1924. El Universo se supone homogéneo (el espacio tiene las mismas propiedades métricas (medidas) en todos los puntos) e isotrópico (el espacio tiene las mismas medidas en todas las direcciones). Las soluciones de Friedmann permiten dos posibles geometrías para el espacio: modelo cerrado con un espacio similar a una bola, curvado hacia afuera ( curvatura positiva ) y modelo abierto con un espacio similar a una silla de montar, curvado hacia el interior ( curvatura negativa). En ambos modelos, el Universo no se detiene, se expande (se hace más grande) o se contrae (se reduce). Esto fue confirmado por Edwin Hubble, quien estableció el desplazamiento al rojo de las galaxias en retroceso del Hubble. El consenso actual es que el modelo isotrópico , en general, proporciona una descripción adecuada del estado actual del Universo; sin embargo, la isotropía del Universo presente en sí misma no es una razón para esperar que sea adecuada para describir las primeras etapas de la evolución del Universo . Al mismo tiempo, es obvio que en el mundo real la homogeneidadEs, en el mejor de los casos, sólo una aproximación. Incluso si se puede hablar de una distribución homogénea de la densidad de la materia a distancias que son grandes en comparación con el espacio intergaláctico, esta homogeneidad se desvanece a escalas más pequeñas. Por otro lado, el supuesto de homogeneidad va muy lejos en un aspecto matemático: hace que la solución sea altamente simétrica, lo que puede impartir propiedades específicas que desaparecen al considerar un caso más general.
Otra propiedad importante del modelo isotrópico es la inevitable existencia de una singularidad temporal : el flujo temporal no es continuo, sino que se detiene o invierte una vez que el tiempo alcanza algún valor (muy grande o muy pequeño). Entre singularidades, el tiempo fluye en una dirección: alejándose de la singularidad ( flecha del tiempo ). En el modelo abierto, hay una singularidad temporal, por lo que el tiempo está limitado en un extremo pero ilimitado en el otro, mientras que en el modelo cerrado hay dos singularidades que limitan el tiempo en ambos extremos ( Big Bang y Big Crunch ).
Las únicas propiedades físicamente interesantes de los tiempos espaciales (como las singularidades) son aquellas que son estables , es decir, aquellas propiedades que todavía ocurren cuando los datos iniciales se perturban ligeramente. Es posible que una singularidad sea estable y, sin embargo, carezca de interés físico: la estabilidad es una condición necesaria pero no suficiente para la relevancia física. Por ejemplo, una singularidad podría ser estable solo en una vecindad de conjuntos de datos iniciales correspondientes a universos altamente anisotrópicos . Dado que el universo real es ahora aparentemente casi isotrópico, tal singularidad no podría ocurrir en nuestro universo. Una condición suficiente para que una singularidad estable sea de interés físico es el requisito de que la singularidad sea genérica.(o general). En términos generales, una singularidad estable es genérica si ocurre cerca de cada conjunto de condiciones iniciales y los campos no gravitacionales están restringidos de alguna manera específica a campos "físicamente realistas", de modo que las ecuaciones de Einstein, varias ecuaciones de estado, etc. Se supone que se aferran a los tiempos espaciales evolucionados. Puede suceder que una singularidad sea estable bajo pequeñas variaciones de los verdaderos gradosgravitatorios de libertad , y sin embargo no sea genérica porque la singularidad depende de alguna manera del sistema de coordenadas , o más bien de la elección de la hipersuperficie inicial desde la cual el espacio-tiempo Se evoluciona.
Para un sistema de ecuaciones diferenciales no lineales , como las ecuaciones de Einstein , una solución generalno se define de forma inequívoca. En principio, puede haber múltiples integrales generales , y cada una de ellas puede contener solo un subconjunto finito de todas las posibles condiciones iniciales . Cada una de esas integrales puede contener todas las funciones independientes requeridas que, sin embargo, pueden estar sujetas a algunas condiciones (por ejemplo, algunas desigualdades).). La existencia de una solución general con una singularidad, por lo tanto, no excluye la existencia de otras soluciones generales adicionales que no contengan una singularidad. Por ejemplo, no hay razón para dudar de la existencia de una solución general sin una singularidad que describa un cuerpo aislado con una masa relativamente pequeña.
Es imposible encontrar una integral general para todo el espacio y para todos los tiempos. Sin embargo, esto no es necesario para resolver el problema: es suficiente estudiar la solución cerca de la singularidad. Esto también resolvería otro aspecto del problema: las características de la evolución métrica del espacio-tiempo en la solución general cuando alcanza la singularidad física, entendida como un punto donde la densidad de la materia y los invariantes del tensor de curvatura de Riemann se vuelven infinitos.
Existencia de singularidad tiempo físico [ editar ]
Uno de los principales problemas estudiados por el grupo de Landau (a los que pertenece BKL) fue si los modelos cosmológicos relativistas necesariamente contienen una singularidad de tiempo o si la singularidad de tiempo es un artefacto de los supuestos utilizados para simplificar estos modelos. La independencia de la singularidad en los supuestos de simetría significaría que las singularidades del tiempo existen no solo en las soluciones especiales, sino también en las generales de las ecuaciones de Einstein. Es razonable sugerir que si una singularidad está presente en la solución general, debe haber algunas indicaciones que se basen solo en las propiedades más generales de las ecuaciones de Einstein, aunque esas indicaciones por sí mismas podrían ser insuficientes para caracterizar la singularidad.
Un criterio para la generalidad de las soluciones es el número de funciones de coordenadas de espacio independientes que contienen. Incluyen solo las funciones "físicamente independientes" cuyo número no puede reducirse por ninguna elección del marco de referencia . En la solución general, el número de tales funciones debe ser suficiente para definir completamente las condiciones iniciales (distribución y movimiento de la materia, distribución del campo gravitatorio ) en algún momento del tiempo elegido como inicial. Este número es cuatro para un espacio vacío (vacío) y ocho para un espacio lleno de materia y / o radiación. [9] [10]
El trabajo previo del grupo Landau [11] [12] [13] (revisado en [9] ) llevó a la conclusión de que la solución general no contiene una singularidad física. Esta búsqueda de una clase más amplia de soluciones con una singularidad se ha hecho, esencialmente, mediante un método de prueba y error, ya que faltaba un enfoque sistemático para el estudio de las ecuaciones de Einstein. Un resultado negativo, obtenido de esta manera, no es convincente por sí mismo; una solución con el grado necesario de generalidad la invalidaría, y al mismo tiempo confirmaría cualquier resultado positivo relacionado con la solución específica.
En ese momento, la única indicación conocida estaba relacionada con la forma de las ecuaciones de Einstein escritas en un cuadro síncrono , es decir, en un cuadro en el que el tiempo apropiado x 0 = t está sincronizado en todo el espacio; en este marco, el elemento de distancia de espacio dl está separado del intervalo de tiempo dt . [14] La ecuación de Einstein.
- ( eq. 1 )
escrito en marco síncrono da un resultado en el que el determinante métrico g inevitablemente se vuelve cero en un tiempo finito independientemente de cualquier suposición sobre la distribución de la materia. [9] [10]
Sin embargo, esta indicación se eliminó una vez que quedó claro que está vinculado con una propiedad geométrica específica del cuadro síncrono: el cruce de las coordenadas de la línea de tiempo. Este cruce tiene lugar en algunas hipersuperficies circundantes que son análogos cuatridimensionales de las superficies cáusticasen la óptica geométrica ; g se convierte en cero exactamente en este cruce. [13] Por lo tanto, aunque esta singularidad es general, es ficticia y no física; desaparece cuando se cambia el marco de referencia. Esto, aparentemente, eliminó el incentivo entre los investigadores para futuras investigaciones en este sentido.
Sin embargo, el interés en este problema volvió a aumentar en la década de 1960 después de que Penrosepublicara sus teoremas [15] que vinculaban la existencia de una singularidad de carácter desconocido con algunos supuestos muy generales que no tenían nada en común con un marco de referencia de elección. Otros teoremas similares fueron encontrados más tarde por Hawking [16] [17] y Geroch [18] (ver teoremas de singularidad de Penrose-Hawking ). Esto reavivó el interés en la búsqueda de soluciones singulares.
Solución homogénea generalizada [ editar ]
En un espacio que es tanto homogéneo como isotrópico, la métrica se determina completamente dejando libre solo el signo de la curvatura. Suponiendo que solo la homogeneidad del espacio sin simetría adicional como la isotropía deja considerablemente más libertad en la elección de la métrica. Lo siguiente se refiere a la parte del espacio de la métrica en un instante dado de tiempo t asumiendo un sistema de referencia de espacio-tiempo síncrono para que t sea el mismo tiempo sincronizado para todo el espacio.
La homogeneidad implica propiedades métricas idénticas en todos los puntos del espacio. Una definición exacta de este concepto implica considerar conjuntos de transformaciones de coordenadas que transforman el espacio en sí mismo, es decir, dejan su métrica sin cambios: si el elemento de línea antes de la transformación es
luego, después de la transformación, el mismo elemento de línea es
con la misma dependencia funcional de γ αβ en las nuevas coordenadas. (Para una definición más teórica y de coordenadas independientes del espacio homogéneo, ver espacio homogéneo ). Un espacio es homogéneo si admite un conjunto de transformaciones ( un grupo de movimientos ) que lleva cualquier punto dado a la posición de cualquier otro punto. Como el espacio es tridimensional, las diferentes transformaciones del grupo se etiquetan mediante tres parámetros independientes.
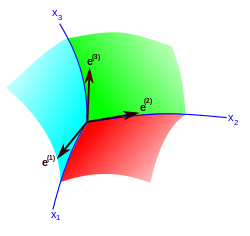
En el espacio euclidiano, la homogeneidad del espacio se expresa por la invariancia de la métrica bajo desplazamientos paralelos ( traducciones ) del sistema de coordenadas cartesiano . Cada traducción está determinada por tres parámetros: los componentes del vector de desplazamiento del origen de coordenadas. Todas estas transformaciones dejan invariantes los tres diferenciales independientes ( dx , dy , dz ) a partir de los cuales se construye el elemento de línea. En el caso general de un espacio homogéneo no euclidiano, las transformaciones de su grupo de movimientos dejan de nuevo invariantes tres formas diferenciales lineales independientes , que, sin embargo, no se reducen aDiferenciales totales de cualquier función de coordenadas. Estas formas están escritas comodonde el índice latino ( a ) etiqueta tres vectores independientes (funciones de coordenadas); estos vectores se llaman un campo de marco o tríada. Las letras griegas etiquetan las tres coordenadas curvilíneas en forma de espacio . Un invariante métrico espacial se construye bajo el grupo de movimientos dado con el uso de las formas anteriores:
- ( ec. 6a )
es decir, el tensor métrico es
- ( ec. 6b )
donde los coeficientes η ab , que son simétricos en los índices a y b , son funciones del tiempo. La elección de los vectores de base está dictada por las propiedades de simetría del espacio y, en general, estos vectores de base no son ortogonales (por lo que la matriz η ab no es diagonal).
- ( ec. 6c )
En el caso tridimensional, la relación entre los dos vectores triples se puede escribir explícitamente
- ( ec. 6d )
donde el volumen v es
con e ( a ) y e ( a ) considerados como vectores cartesianos con componentes y , respectivamente. El determinante del tensor métrico eq. 6b es γ = η v 2 donde η es el determinante de la matriz η ab .
Las condiciones requeridas para la homogeneidad del espacio son:
- ( eq. 6e )
- ( eq. 6f )
La ecuación 6e se puede escribir en forma vectorial como
donde nuevamente las operaciones vectoriales se realizan como si las coordenadas x α fueran cartesianas. Utilizando eq. 6d , se obtiene
- ( eq. 6g )
y seis ecuaciones más obtenidas por una permutación cíclica de los índices 1, 2, 3.
Las constantes de estructura son antisimétricas en sus índices más bajos, como se ve en su definición eq. 6e :. Otra condición en las constantes de la estructura se puede obtener al observar que la ec. 6f se puede escribir en forma de relaciones de conmutación
- ( eq. 6h )
para los operadores diferenciales lineales
- ( eq. 6i )
En la teoría matemática de grupos continuos (grupos de Lie ) los operadores X a satisfacen las condiciones de la forma eq. 6h se llaman los generadores del grupo . Sin embargo, para evitar confusiones cuando se compara con otras presentaciones, se debe mencionar que la teoría sistemática generalmente comienza con operadores definidos utilizando los vectores de Matanza. (ya que en la métrica síncrona ninguno de los componentes γ αβdepende del tiempo, los vectores de Killing son como el tiempo):
La condición mencionada anteriormente se desprende de la identidad jacobi.
y tiene la forma
- ( eq. 6j )
Es una ventaja definitiva de usar, en lugar de las constantes de tres índices , un conjunto de cantidades de dos índices, obtenidas por la transformación dual
- ( eq. 6k )
donde e abc = e abc es el símbolo antisimétrico de la unidad (con e 123 = +1). Con estas constantes las relaciones de conmutación eq. 6h se escriben como
- ( eq. 6l )
La propiedad antisimetría ya se tiene en cuenta en la definición eq. 6k , mientras que la propiedad eq. 6j toma la forma
- ( eq. 6m )
La elección de los tres vectores de marco en las formas diferenciales. (y con ellos los operadores X a ) no son únicos. Pueden ser sometidos a cualquier transformación lineal con coeficientes constantes:
- ( eq. 6n )
Las cantidades η ab y C ab se comportan como tensores (son invariantes) con respecto a tales transformaciones.
Las condiciones eq. Los 6m son los únicos que deben satisfacer las constantes de estructura. Pero entre las constantes admisibles por estas condiciones, hay conjuntos equivalentes, en el sentido de que su diferencia está relacionada con una transformación del tipo eq. 6n . La cuestión de la clasificación de los espacios homogéneos se reduce a determinar todos los conjuntos no equivalentes de constantes de estructura. Esto se puede hacer, usando las propiedades "tensoriales" de las cantidades C ab , por el siguiente método simple (CG Behr, 1962).
El "tensor" asimétrico C ab puede resolverse en una parte simétrica y una antisimétrica. El primero se denota por n ab , y el segundo se expresa en términos de su " vector dual " a c :
- ( eq. 6o )
- ( eq. 6p )
Por medio de las transformaciones eq. 6m el "tensor" simétrico n ab se puede llevar a la forma diagonal con valores propios n 1 , n 2 , n 3 . La ecuación 6p muestra que el "vector" a b (si existe) se encuentra en una de las direcciones principales del "tensor" n ab , la que corresponde al valor propio cero. Sin pérdida de generalidad, por lo tanto, se puede establecer un b = ( a , 0, 0). Entonces eq. 6p reduce a un 1 = 0, es decir, una de las cantidadesa o n 1 debe ser cero. Las identidades jacobi toman la forma:
- ( eq. 6q )
La única libertad restante es un cambio de signo de los operadores X a y transformaciones de escala arbitrarias de los mismos (multiplicación por constantes). Esto permite que nosotros al mismo tiempo para cambiar el signo de todos los n una y también para que la cantidad de un positivo (si es diferente de cero). También todas las constantes de estructura pueden hacerse iguales a ± 1, si al menos una de las cantidades a , n 2 , n 3 sedesvanece. Pero si las tres de estas cantidades difieren de cero, las transformaciones de escala dejan invariable la relación h = a 2 ( n 2 n 3 )–1 .
De este modo, se llega a la clasificación de Bianchi que enumera los posibles tipos de espacios homogéneos clasificados por los valores de a , n 1 , n 2 , n 3, que se presenta gráficamente en la Fig. 3. En el caso de la clase A ( a = 0), escriba IX ( n (1) = 1, n (2) = 1, n (3) = 1) está representado por el octante 2, tipo VIII ( n (1) = 1, n (2) = 1, n (3) = –1) está representado por el octante 6, mientras que el tipo VII0 ( n (1) = 1, n (2) = 1, n (3) = 0) está representado por el primer cuadrante del plano horizontal y tipo VI 0 ( n (1) = 1, n (2) = –1, n (3) = 0) está representado por el cuarto cuadrante de este plano; tipo II (( n (1) = 1, n (2) = 0, n (3) = 0) está representado por el intervalo [0,1] a lo largo de n (1) y tipo I ( n (1) = 0 , n (2)= 0, n (3) = 0) está en el origen. De manera similar, en el caso de clase B (con n (3) = 0), Bianchi tipo VI h ( a = h , n (1) = 1, n (2) = –1) se proyecta al cuarto cuadrante del plano horizontal y el tipo VII h ( a = h , n (1) = 1, n (2) = 1) se proyecta al primer cuadrante del plano horizontal; estos dos últimos tipos son una única clase de isomorfismo correspondiente a una superficie de valor constante de la función h = a2 ( n (1) n (2) ) −1 . Una típica de estas superficies se ilustra en un octante, el ángulo θ dado por tan θ = | h / 2 | 1/2 ; aquellos en los octantes restantes se obtienen por rotación a través de múltiplos de π / 2, halternando en signo para una magnitud dada | h |. El tipo III es un subtipo de VI h con a = 1. Tipo V ( a = 1, n (1)= 0, n (2) = 0) es el intervalo (0,1] a lo largo del ejeuna y tipo IV ( un = 1, n (1) = 1, n (2) = 0) es la cara abierta vertical entre el primer y cuarto cuadrantes del un = 0 plano con esta última dando la clase de valor límite de cada tipo.






















![{\ displaystyle \ left [X_ {a}, X_ {b} \ right] \ equiv X_ {a} X_ {b} -X_ {b} X_ {a} = C_ {ab} ^ {c} X_ {c} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe8fb3e8dae606acce90cc9a9902fb4d7b2492b)



![{\ displaystyle [[X_ {a}, X_ {b}], X_ {c}] + [[X_ {b}, X_ {c}], X_ {a}] + [[X_ {c}, X_ { a}], X_ {b}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b257669da84cabe273a083e469cdb1accdb50d23)








![{\ displaystyle [X_ {1}, X_ {2}] = - aX_ {2} + n_ {3} X_ {3}, \ quad [X_ {2}, X_ {3}] = n_ {1} X_ { 1}, \ quad [X_ {3}, X_ {1}] = n_ {2} X_ {2} + aX_ {3}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4be2d14a88dbd4628d84fba5ab875ed708c2593)
No hay comentarios:
Publicar un comentario