Estos 135 politopos se muestran cada uno en estos 7 planos de simetría, con vértices y bordes dibujados, y vértices coloreados por el número de vértices superpuestos en cada posición proyectiva.
El postulado de AA se deduce del hecho de que la suma de los ángulos interiores de un triángulo es siempre igual a 180 °. Al conocer dos ángulos, como 32 ° y 64 ° grados, sabemos que el siguiente ángulo es 84 °, porque 180- (32 + 64) = 84. (Esto se refiere a veces como el Postulado AAA, que es cierto en todos los aspectos, pero dos ángulos son completamente suficientes).
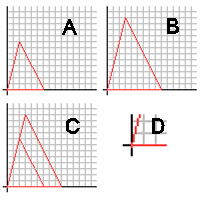
El postulado se puede entender mejor trabajando en orden inverso. Los dos triángulos en las cuadrículas A y B son similares , por una dilatación 1.5 desde A hasta B. Si están alineados, como en la cuadrícula C, es evidente que el ángulo en el origen es congruente con el otro (D). También sabemos que el par de lados opuestos al origen son paralelos. Lo sabemos porque los pares de lados que los rodean son similares, se derivan del mismo punto y se alinean entre sí. Luego podemos mirar los lados alrededor de los paralelos como transversales , y por lo tanto los ángulos correspondientes son congruentes. Usando este razonamiento podemos decir que los triángulos similares tienen ángulos congruentes.
Adrianus Willem "Aad" van der Vaart (nacido el 12 de julio de 1959) es un profesor holandés de Estocásticos en el Instituto de Matemáticas de la Universidad de Leiden .
En 2010 fue un orador invitado en el ICM en Hyderabad. [3] En 2015, fue uno de los cuatro ganadores del premio holandés Spinoza y recibió una subvención de 2,5 millones de euros. [4] Fue galardonado con el premio por su investigación sobre modelos matemáticos que ayudan a rastrear genes para la investigación del cáncer. [5] Al recibir el premio, Van der Vaart declaró que 2,5 millones de euros era demasiado, afirmando que podía tener 35 postdoctorales y Ph.D. Los alumnos trabajan con la beca. [6]
También recibió una subvención ERC Advanced en 2012.
En informática teórica , la conjetura de Aanderaa-Karp-Rosenberg(también conocida como la conjetura de Aanderaa-Rosenberg o la conjetura de evasividad ) es un grupo de conjeturas relacionadas sobre el número de preguntas de la forma "¿Hay un borde entre el vértice u y el vértice? v ? " que deben responderse para determinar si un gráfico no dirigido tiene o no una propiedad particular como la planaridad o la bipartidad . Ellos llevan el nombre de Stål Aanderaa , Richard M. Karp y Arnold L. Rosenberg. De acuerdo con la conjetura, para una amplia clase de propiedades, ningún algoritmo puede garantizar que será capaz de saltear cualquier pregunta: cualquier algoritmo para determinar si el gráfico tiene la propiedad, no importa lo inteligente que sea, podría necesitar examinar cada par de vértices Antes de que pueda dar su respuesta. Una propiedad que satisface esta conjetura se llama evasiva .
Más precisamente, la conjetura de Aanderaa-Rosenberg afirma que cualquier algoritmo determinista debe probar al menos una fracción constante de todos los pares de vértices posibles, en el peor de los casos , para determinar cualquier propiedad de gráfico monótono no trivial; en este contexto, una propiedad es monótona si permanece verdadera cuando se agregan bordes (por lo que la planaridad no es monótona, pero la no planaridad es monótona). Una versión más sólida de esta conjetura, llamada conjetura de evasividad o la conjetura de Aanderaa-Karp-Rosenberg, indica que se necesitan exactamente n ( n - 1) / 2 pruebas. Las versiones del problema para algoritmos aleatorios y algoritmos cuánticos también se han formulado y estudiado.
La conjetura determinista de Aanderaa-Rosenberg fue demostrada por Rivest y Vuillemin (1975) , pero la conjetura más fuerte de Aanderaa-Karp-Rosenberg aún no se ha probado. Además, existe una gran brecha entre el límite inferior conjeturado y el límite inferior mejor comprobado para la complejidad de consultas aleatorias y cuánticas.
La propiedad de no estar vacío (es decir, tener al menos un borde) es monótona, porque agregar otro borde a un gráfico no vacío produce otro gráfico no vacío. Hay un algoritmo simple para probar si un gráfico no está vacío: recorra todos los pares de vértices, y verifique si cada par está conectado por un borde. Si alguna vez se encuentra un borde de esta manera, salga del bucle, e informe que el gráfico no está vacío, y si el bucle se completa sin encontrar bordes, informe que el gráfico está vacío. En algunos gráficos (por ejemplo, los gráficos completos ) este algoritmo terminará rápidamente, sin probar cada par de vértices, pero en el gráfico vacíoprueba todos los pares posibles antes de terminar. Por lo tanto, la complejidad de consulta de este algoritmo es n( n - 1) / 2: en el peor de los casos, el algoritmo realiza n ( n - 1) / 2 pruebas.
El algoritmo descrito anteriormente no es el único método posible de prueba de no vacío, pero la conjetura de Aanderaa-Karp-Rosenberg implica que todo algoritmo determinista para probar el no vacío tiene la misma complejidad de consulta, n ( n - 1) / 2. Es decir, la propiedad de no estar vacío es evasiva . Para esta propiedad, el resultado es fácil de probar directamente: si un algoritmo no realiza n ( n - 1) / 2 pruebas, no puede distinguir el gráfico vacío de un gráfico que tiene un borde que conecta uno de los pares de vértices no probados, y debe dar una respuesta incorrecta en uno de estos dos gráficos.
Definiciones [ editar ]
En el contexto de este artículo, todos los gráficos serán simples y no dirigidos , a menos que se indique lo contrario. Esto significa que los bordes del gráfico forman un conjunto (y no un conjunto múltiple ) y cada borde es un par de vértices distintos. Se supone que los gráficos tienen una representación implícita en la que cada vértice tiene un identificador o etiqueta único y en la que es posible probar la adyacencia de dos vértices cualquiera, pero para la cual la prueba de adyacencia es la única operación primitiva permitida.
De manera informal, una propiedad de gráfico es una propiedad de un gráfico que es independiente del etiquetado. Más formalmente, una propiedad de gráfico es una asignación del conjunto de todos los gráficos a {0,1}, de manera que los gráficos isomorfos se asignan al mismo valor. Por ejemplo, la propiedad de contener al menos 1 vértice de grado 2 es una propiedad de gráfico, pero la propiedad de que el primer vértice tiene grado 2 no lo es, porque depende de la etiqueta del gráfico (en particular, depende de qué vértice es el "primer" vértice). Una propiedad de gráfico se llama no trivial si no asigna el mismo valor a todos los gráficos. Por ejemplo, la propiedad de ser un gráfico es una propiedad trivial, ya que todos los gráficos poseen esta propiedad. Por otro lado, la propiedad de estar vacío no es trivial, porque el gráfico vacíoPosee esta propiedad, pero los gráficos no vacíos no. Se dice que una propiedad de gráfico es monótona si la adición de bordes no destruye la propiedad. Alternativamente, si un gráfico posee una propiedad monótona, entonces cada supergrafo de este gráfico en el mismo conjunto de vértices también lo posee. Por ejemplo, la propiedad de ser no plano es monótono: un supergrafo de un gráfico no plano no es en sí mismo plano. Sin embargo, la propiedad de ser regular no es monótona.
La notación O grande se usa a menudo para la complejidad de la consulta. En resumen, f ( n ) es O ( g ( n )) si para n lo suficientemente grande , f ( n ) ≤ c g ( n ) para alguna constante positiva c . De manera similar, f ( n ) es Ω ( g ( n )) si para n lo suficientemente grande , f ( n ) ≥ c g ( n ) para alguna constante positiva c . Finalmente, f ( n) es Θ ( g ( n )) si es tanto O ( g ( n )) como Ω ( g ( n )).
Complejidad de la consulta [ editar ]
La complejidad de la consulta determinista de evaluar una función en n bits ( x 1 , x 2 , ..., x n ) es el número de bits x i que un algoritmo determinístico debe leer en el peor de los casos para determinar el valor de la función. Por ejemplo, si la función toma el valor 0 cuando todos los bits son 0 y toma el valor 1 de lo contrario (esta es la función OR ), entonces la complejidad de la consulta determinista es exactamente n . En el peor de los casos, la primera n - 1.todos los bits leídos pueden ser 0, y el valor de la función ahora depende del último bit. Si un algoritmo no lee este bit, podría dar una respuesta incorrecta. (Estos argumentos se conocen como argumentos adversarios). El número de bits leídos también se denomina número de consultas realizadas a la entrada. Uno puede imaginar que el algoritmo pregunta (o consulta) la entrada de un bit en particular y la entrada responde a esta consulta.
La complejidad de la consulta aleatoria de la evaluación de una función se define de manera similar, excepto que se permite que el algoritmo sea aleatorio, es decir, puede lanzar monedas y usar el resultado de estas monedas para decidir qué bits consultar. Sin embargo, el algoritmo aleatorio todavía debe generar la respuesta correcta para todas las entradas: no está permitido cometer errores. Dichos algoritmos se denominan algoritmos de Las Vegas , que los distinguen de los algoritmos de Monte Carlo que pueden cometer algún error. La complejidad de las consultas aleatorias también se puede definir en el sentido de Monte Carlo, pero la conjetura de Aanderaa-Karp-Rosenberg se refiere a la complejidad de las propiedades gráficas de la consulta de Las Vegas.
La complejidad de las consultas cuánticas es la generalización natural de la complejidad de las consultas aleatorias, que por supuesto permite consultas y respuestas cuánticas. La complejidad de la consulta cuántica también se puede definir con respecto a los algoritmos de Monte Carlo o los algoritmos de Las Vegas, pero generalmente se entiende como algoritmos cuánticos de Monte Carlo.
En el contexto de esta conjetura, la función a evaluar es la propiedad de gráfico, y la entrada es una cadena de tamaño n ( n - 1) / 2, que proporciona las ubicaciones de los bordes en un gráfico de n vértices, ya que un gráfico puede tener como máximo n ( n - 1) / 2 bordes posibles. La complejidad de la consulta de cualquier función está limitada por n ( n - 1) / 2, ya que toda la entrada se lee después de realizar n ( n - 1) / 2 consultas, lo que determina el gráfico de entrada completamente.
Complejidad determinista de la consulta [ editar ]
Para algoritmos deterministas, Rosenberg (1973) originalmente conjeturó que para todas las propiedades de gráficos no triviales en n vértices, decidir si un gráfico posee esta propiedad requiere consultas Ω ( n 2 ). La condición de no trivialidad es claramente necesaria porque existen propiedades triviales como "¿es esto un gráfico?" El cual puede ser respondido sin ninguna duda.

Una gráfica de escorpión. Uno de los tres vértices del camino rojo es adyacente a todos los otros vértices y los otros dos vértices rojos no tienen otras adyacencias.
La conjetura fue refutada por Aanderaa, quien exhibió una propiedad de gráfico dirigido (la propiedad de contener un "sumidero") que solo requería de O ( n ) consultas para probar. Un sumidero , en un gráfico dirigido, es un vértice del grado n -1 y el grado 0. Esta propiedad se puede probar con menos de 3 n consultas ( Best, van Emde Boas & Lenstra 1974 ). Una propiedad de gráfico no dirigida que también se puede probar con consultas O ( n ) es la propiedad de ser un gráfico de escorpión, descrito por primera vez en Best, van Emde Boas & Lenstra (1974). Un gráfico de escorpión es un gráfico que contiene una ruta de tres vértices, de manera que un punto final de la ruta está conectado a todos los vértices restantes, mientras que los otros dos vértices de ruta no tienen bordes incidentes distintos a los de la ruta.
Richard Karp conjeturó la afirmación más fuerte (que ahora se llama la conjetura de evasividad o la conjetura de Aanderaa-Karp-Rosenberg ) de que "toda propiedad de gráfico monótono no trivial para gráficos en nvértices es evasiva". [2] Una propiedad se llama evasiva si determinar si un gráfico dado tiene esta propiedad a veces requiere todas las n ( n - 1) / 2 consultas. [3] Esta conjetura dice que el mejor algoritmo para probar cualquier propiedad monótona no trivial debe (en el peor de los casos) consultar todos los bordes posibles. Esta conjetura aún está abierta, aunque varias propiedades gráficas especiales han demostrado ser evasivas para todas las n.. La conjetura se resolvió para el caso en que n es un poder primordial de Kahn, Saks & Sturtevant (1983) utilizando un enfoque topológico . La conjetura también se ha resuelto para todas las propiedades monótonas no triviales en los gráficos bipartitos de Yao (1988) . Las propiedades cerradas de menor importancia también han demostrado ser evasivas para n grandes ( Chakrabarti, Khot y Shi 2001 ).
Complejidad de consultas aleatorias [ editar ]
Richard Karp también conjeturó que se requieren Ω ( n 2 ) consultas para probar propiedades monótonas no triviales incluso si se permiten algoritmos aleatorios. Ninguna propiedad monótona no trivial que se conoce que requiere menos de n 2 /4 consultas para probar. Un límite inferior lineal (es decir, Ω ( n )) en todas las propiedades monótonas se deriva de una relación muy general entre las complejidades de consultas aleatorias y deterministas . El primer límite inferior superlineal para todas las propiedades monótonas fue dado por Yao (1991) que mostró que se requieren consultas Ω ( n log 1/12 n ). Esto fue mejorado aún más por King (1988) a Ω ( n5/4 ), y luego por Hajnal (1991) a Ω ( n 4/3 ). Esto se mejoró posteriormente a la corriente más conocido cota inferior (entre límites que mantienen para todas las propiedades monótonas) de Ω ( n 4/3 log 1/3 n ) por Chakrabarti y Khot (2001) .
Algunos resultados recientes dan límites más bajos que están determinados por la probabilidad crítica p de la propiedad de gráfico monótono en consideración. La probabilidad crítica p se define como la única p tal que un gráfico aleatorio G ( n , p ) posee esta propiedad con probabilidad igual a 1/2. Un gráfico aleatorio G ( n , p ) es un gráfico en n vértices donde se elige que cada borde esté presente con probabilidad p independiente de todos los otros bordes. Friedgut, Kahn & Wigderson (2002) mostraron que cualquier propiedad monótona con probabilidad críticap requiere{\ displaystyle \ Omega \ left (\ min \ left \ {{\ frac {n} {\ min (p, 1-p)}}, {\ frac {n ^ {2}} {\ log n}} \ bien bien)} consultas Para el mismo problema, O'Donnell et al. (2005) mostró un límite inferior de Ω ( n 4/3 / p 1/3 ).
consultas Para el mismo problema, O'Donnell et al. (2005) mostró un límite inferior de Ω ( n 4/3 / p 1/3 ).
Al igual que en el caso determinista, hay muchas propiedades especiales para las cuales se conoce un límite inferior de Ω ( n 2 ). Además, se conocen mejores límites inferiores para varias clases de propiedades gráficas. Por ejemplo, para probar si la gráfica tiene un subgrafo isomorfo a cualquier grafica dada (el llamado problema de isomorfismo subgraph ), el límite inferior mejor conocido es Ω ( n 3/2 ) debido a Gröger (1992) .
Complejidad de la consulta cuántica [ editar ]
Para la complejidad de la consulta cuántica de error limitado , el límite inferior más conocido es Ω ( n 2/3 log 1/6 n) como lo observa Andrew Yao. [4] Se obtiene combinando el límite inferior aleatorio con el método del adversario cuántico. El mejor límite inferior posible que podría esperarse alcanzar es Ω ( n ), a diferencia del caso clásico, debido al algoritmo de Grover que proporciona un algoritmo de consulta O ( n ) para probar la propiedad monótona de la no vacuidad. Similar al caso determinista y aleatorizado, hay algunas propiedades que se sabe que tienen un Ω ( n) Límite inferior, por ejemplo, no vacío (que se sigue de la optimalidad del algoritmo de Grover) y la propiedad de contener un triángulo . Hay algunas propiedades gráficas que se sabe que tienen un límite inferior Ω ( n 3/2 ), e incluso algunas propiedades con un límite inferior Ω ( n 2 ). Por ejemplo, la propiedad monótona de la no planaridad requiere Θ ( n 3/2 ) consultas ( Ambainis et al. 2008 ) y la propiedad monótona de contener más de la mitad del número posible de bordes (también llamada función de la mayoría) requiere ( n 2 ) consultas ( Beals et al. 2001 ).


No hay comentarios:
Publicar un comentario