APUNTES DE GEODESIA

Engels Maps es una compañía de mapas en el valle de Ohio con especial concentración en la región de Cincinnati - Dayton . ^[1] También produce mapas de cámara de comercio .

Publicaciones [ editar ]

Cuenta con tres publicaciones semestrales que forman su fundación:

• Guía de Cincinnati Engels
• Guía de Dayton Engels
• Guía de Indianapolis Engels

Sus mapas también se encuentran en las páginas amarillas de Cincinnati Bell y en el libro de trabajo de Dayton .

Historia corporativa [ editar ]

Engels Maps fue fundada por Judson Engels en 1994.

El efecto Eötvös es el cambio en la fuerza gravitacional percibida causada por el cambio en la aceleración centrífuga que resulta de la velocidad en dirección este o oeste. Al moverse hacia el este, la velocidad angular del objeto aumenta (además de la rotación de la Tierra ) y, por lo tanto, la fuerza centrífuga también aumenta, causando una reducción percibida en la fuerza gravitacional.

A principios de la década de 1900 (década), un equipo alemán del Instituto de Geodesia en Potsdam realizó mediciones de gravedad en barcos en movimiento en los océanos Atlántico, Índico y Pacífico. Mientras estudiaban los resultados, el noble y físico húngaro Baron Roland von Eötvös ( Loránd Eötvös ) notó que las lecturas eran más bajas cuando el barco se movía hacia el este, más alto cuando se movía hacia el oeste. Él identificó esto como principalmente una consecuencia de la rotación de la tierra. En 1908 se realizaron nuevas mediciones en el Mar Negro en dos barcos, uno que se desplazaba hacia el este y otro hacia el oeste. Los resultados fundamentaron la afirmación de Eötvös. Desde entonces, los geodesistas utilizan la siguiente fórmula para corregir la velocidad relativa a la Tierra durante una ejecución de medición.

$${\ displaystyle a_ {r} = 2 \ Omega u \ cos \ phi + {\ frac {u ^ {2} + v ^ {2}} {R}}.

Aquí,

$${\ displaystyle a_ {r}} es la aceleración relativa

$${\ displaystyle \ Omega} Es la tasa de rotación de la Tierra.

$${\ displaystyle u} es la velocidad en dirección longitudinal (este-oeste)

$${\ displaystyle \ phi} Es la latitud donde se toman las medidas.

$${\ displaystyle v} es la velocidad en dirección latitudinal (norte-sur)

$${\ displaystyle R} es el radio de la tierra

El primer término en la fórmula, 2 Ωu  cos (φ), corresponde al efecto Eötvös. El segundo término es un refinamiento que, en circunstancias normales, es mucho más pequeño que el efecto Eötvös.

Explicación física [ editar ]

El diseño más común para un gravímetro para trabajo de campo es un diseño basado en resortes; Un resorte que suspende un peso interno. La fuerza de suspensión proporcionada por el resorte contrarresta la fuerza gravitacional. Un resorte bien fabricado tiene la propiedad de que la cantidad de fuerza que ejerce el resorte es proporcional a la extensión del resorte desde su posición de equilibrio ( ley de Hooke ). Cuanto más fuerte sea la gravedad efectiva en una ubicación particular, más se extiende el resorte; el resorte se extiende hasta una longitud en la que se sostiene el peso interno. Además, las partes móviles del gravímetro se humedecerán, para que sea menos susceptible a las influencias externas, como la vibración.

Para los cálculos se supondrá que el peso interno tiene una masa de diez kilogramos (10 kg; 10,000 g). Se supondrá que para el levantamiento se usa un método de transporte que proporciona una buena velocidad mientras se mueve muy suavemente: una aeronave. Deje que la velocidad de crucero de la aeronave sea de 25 metros por segundo (90 km / h; 56 mph).

Movimiento a lo largo del ecuador [ editar ]

Gráfico de la fuerza experimentada por un objeto de 10 kilogramos en función de su velocidad que se mueve a lo largo del ecuador de la Tierra (medida dentro del marco giratorio). (La fuerza positiva en el gráfico se dirige hacia arriba. La velocidad positiva se dirige hacia el este y la velocidad negativa hacia el oeste).

Para calcular qué se necesita para que el peso interno de un gravímetro se suspenda neutralmente cuando está estacionario con respecto a la Tierra, se debe tener en cuenta la rotación de la Tierra. En el ecuador, la velocidad de la superficie de la Tierra es de unos 465 metros por segundo (1.674 km / h; 1.040 mph). La cantidad de fuerza centrípeta requerida para hacer que un objeto se mueva a lo largo de una trayectoria circular con un radio de 6378 kilómetros (el radio ecuatorial de la Tierra), a 465 m / s, es de aproximadamente 0.034 newtons por kilogramo de masa. Para un peso interno de 10,000 gramos, eso equivale a unos 0,34 newtons. La cantidad de fuerza de suspensión requerida es la masa del peso interno (multiplicado por la aceleración de la gravedad) menos esos 0.34 newtons. En otras palabras: cualquier objeto que gire conjuntamente con la Tierra en el ecuador tiene su peso medido reducido en un 0,34 por ciento,

Cuando se navega a 10 m / s al este, la velocidad total llega a 465 + 10 = 475 m / s, lo que requiere una fuerza centrípeta de aproximadamente 0.0354 newtons por kilogramo. Navegando a 10 m / s debido al oeste, la velocidad neta es 465 - 10 = 455 m / s, lo que requiere alrededor de 0.0325 newtons por kilogramo. Por lo tanto, si el peso interno se suspende de manera neutral mientras se navega hacia el Este, después de invertir el rumbo, ya no se suspenderá de forma neutral: la masa aparente del peso interno de 10,000 gramos aumentará en aproximadamente 3 gramos, y el resorte del gravímetro debe extenderse Algunos más para acomodar este mayor peso.

En los modelos meteorológicos de alto rendimiento, este efecto debe tenerse en cuenta a escala terrestre. Las masas de aire con una velocidad significativa con respecto a la Tierra tienen una tendencia a migrar a otra altitud, y cuando las exigencias de precisión son estrictas, esto debe tenerse en cuenta.

Derivación de la fórmula para caso simplificado [ editar ]

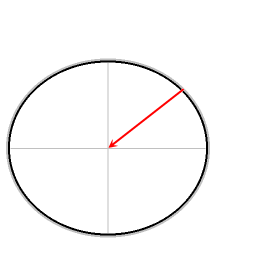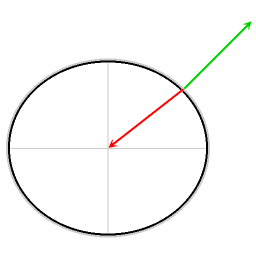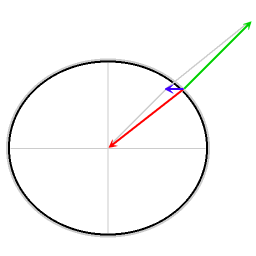
Derivación de la fórmula para el movimiento a lo largo del ecuador.

Un sistema de coordenadas conveniente en esta situación es el sistema de coordenadas inercial que se mueve conjuntamente con el centro de masa de la Tierra. Entonces, lo siguiente es válido: los objetos que están en reposo en la superficie de la Tierra, girando conjuntamente con la Tierra, están rodeando el eje de la Tierra, por lo que están en aceleración centrípeta con respecto a ese sistema de coordenadas inercial.

Lo que se busca es la diferencia en la aceleración centrípeta de la aeronave topográfica entre estar parado con respecto a la Tierra y tener una velocidad con respecto a la Tierra. La siguiente derivación es exclusivamente para movimiento en dirección este-oeste o oeste-este.

Notación:

$${\ displaystyle a_ {u}} es la aceleración centrípeta total cuando se mueve a lo largo de la superficie de la Tierra.

$${\ displaystyle a_ {s}} Es la aceleración centrípeta cuando está estacionaria con respecto a la Tierra.

$${\ displaystyle \ Omega}Es la velocidad angular de la Tierra: una revolución por día sideral .

$${\ displaystyle \ omega _ {r}} es la velocidad angular de la aeronave en relación con la velocidad angular de la Tierra.

$${\ displaystyle \ left (\ Omega + \ omega _ {r} \ right)} Es la velocidad angular total de la aeronave.

$${\ displaystyle u = \ omega _ {r} R} es la velocidad de la aeronave (velocidad relativa a la Tierra).

$${\ displaystyle R} es el radio de la tierra.

{\ displaystyle {\ begin {alineado} a_ {r} & = a_ {u} -a_ {s} \\ & = \ left (\ Omega + \ omega _ {r} \ right) ^ {2} R- \ Omega ^ {2} R \\ & = \ Omega ^ {2} R + 2 \ Omega \ omega _ {r} R + \ omega _ {r} ^ {2} R- \ Omega ^ {2} R \\ & = 2 \ Omega \ omega _ {r} R + \ omega _ {r} ^ {2} R \\ & = 2 \ Omega u + {\ frac {u ^ {2}} {R}} \\\ final {alineado }}}

Se puede ver fácilmente que en el caso del movimiento a lo largo del ecuador, la fórmula para cualquier latitud se simplifica en la fórmula anterior.

$${\ displaystyle a_ {r} = 2 \ Omega u \ cos \ phi + {\ frac {u ^ {2} + v ^ {2}} {R}}}

El segundo término representa la aceleración centrípeta requerida para que la aeronave siga la curvatura de la tierra. Es independiente tanto de la rotación de la Tierra como de la dirección del movimiento. Por ejemplo, cuando un avión que transporta instrumentos de lectura gravimétrica cruza uno de los polos a una altitud constante, la trayectoria del avión sigue la curvatura de la tierra. El primer término en la fórmula es cero entonces, debido a que el coseno del ángulo es cero, y el segundo término representa la aceleración centrípeta para seguir la curvatura de la superficie de la Tierra.

Explicación del coseno en el primer término [ editar ]

La fuerza de la gravedad y la fuerza normal . La fuerza resultante actúa como la fuerza centrípeta requerida.

La derivación matemática del efecto de Eötvös para el movimiento a lo largo del ecuador explica el factor 2 en el primer término de la fórmula de corrección de Eötvös. Lo que queda por explicar es el factor coseno.

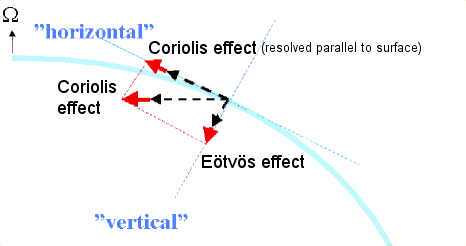
Debido a su rotación, la Tierra no tiene forma esférica, hay una protuberancia ecuatorial . La fuerza de la gravedad se dirige hacia el centro de la Tierra. La fuerza normal es perpendicular a la superficie local.

En los polos y en el ecuador, la fuerza de la gravedad y la fuerza normal están exactamente en dirección opuesta. En cada otra latitud, las dos no son exactamente opuestas, por lo que hay una fuerza resultante, que actúa hacia el eje de la Tierra. En cada latitud hay precisamente la cantidad de fuerza centrípeta que es necesaria para mantener un espesor uniforme de la capa atmosférica. (La Tierra sólida es dúctil. Cuando la forma de la Tierra sólida no está completamente en equilibrio con su velocidad de rotación, la tensión de cizallamientodeforma la Tierra sólida durante un período de millones de años hasta que se resuelve la tensión de cizalla).

Nuevamente, el ejemplo de una aeronave es conveniente para discutir las fuerzas que están actuando. Cuando la aeronave tiene una velocidad relativa a la Tierra en dirección latitudinal, entonces el peso de la aeronave no es el mismo que cuando la aeronave está estacionaria con respecto a la Tierra.

Si una aeronave tiene una velocidad hacia el este, entonces la aeronave en cierto sentido está "acelerando". La situación es comparable a la de un auto de carreras en un circuito cerrado con una superficie de la carretera extremadamente resbaladiza. Si el coche de carreras va demasiado rápido, entonces el coche se moverá a gran velocidad. Para una aeronave en vuelo eso significa una reducción del peso, en comparación con el peso cuando está parado con respecto a la Tierra.

Si la aeronave tiene una velocidad hacia el oeste, entonces la situación es como la de un auto de carreras en un circuito cerrado que va demasiado lento: en una superficie resbaladiza, el automóvil se desplomará. Para una aeronave que significa un aumento del peso.

El primer término del efecto Eötvös es proporcional al componente de la fuerza centrípeta requerida perpendicular a la superficie local de la Tierra, y por lo tanto se describe mediante una ley del coseno: cuanto más cerca del ecuador, más fuerte es el efecto.

Movimiento a lo largo de 60 grados de latitud [ editar ]

El efecto Eötvös para un objeto que se mueve hacia el este a lo largo de 60 grados de latitud. El objeto tiende a alejarse del eje de la Tierra.

El efecto Eötvös para un objeto que se mueve hacia el oeste a lo largo de 60 grados de latitud. El objeto tiende a ser tirado hacia el eje de la Tierra.

Se vuelve a utilizar el mismo gravímetro, su peso interno tiene una masa de 10.000 gramos.

Cálculo de la reducción de peso cuando está estacionario con respecto a la Tierra: 
un objeto ubicado a 60 grados de latitud, en movimiento conjunto con la Tierra, sigue una trayectoria circular, con un radio de aproximadamente 3190 kilómetros y una velocidad de aproximadamente 233 m / s . Esa trayectoria circular requiere una fuerza centrípeta de alrededor de 0.017 newton por cada kilogramo de masa; 0.17 newton para el peso interno de 10,000 gramos. A 60 grados de latitud, la componente que es perpendicular a la superficie local (la vertical local) es la mitad de la fuerza total. Por lo tanto, a 60 grados de latitud, cualquier objeto que se mueva con la Tierra reduce su peso en aproximadamente un 0.08 por ciento, gracias a la rotación de la Tierra.

Cálculo del efecto de Eötvös: 
cuando la aeronave navega a 25 m / s hacia el este, la velocidad total se convierte en 233 + 25 = 258 m / s, lo que requiere una fuerza centrípeta de aproximadamente 0.208 newton; Componente vertical local sobre 0.104 newton. Navegando a 25 m / s hacia el oeste, la velocidad total se convierte en 233 - 25 = 208 m / s, lo que requiere una fuerza centrípeta de aproximadamente 0.135 newton; Componente vertical local sobre 0.068 newton. Por lo tanto, a 60 grados de latitud, la diferencia antes y después del giro en U del peso interno de 10,000 gramos es una diferencia de 4 gramos en el peso medido. (Hablado popularmente como el peso es una fuerza que se mide en newtons, no en gramos).

Los diagramas también muestran el componente en la dirección paralela a la superficie local. En meteorología y en oceanografía , es habitual referirse a los efectos del componente paralelo a la superficie local como el efecto Coriolis .