Cinemática
aceleración normal
Galileo y Descartes ya reconocieron que una partícula que describe un movimiento circular uniforme tiene aceleración. Huygens fue el primero que resolvió este problema. Sin embargo, el procedimiento empleado por Newton para deducir la fórmula de la aceleración normal tiene la ventaja de ser mucho más fácil de entender.
La deducción de la fórmula de la aceleración normal se basa en el análisis de la trayectoria poligonal que sigue una partícula que choca contra una superficie cilíndrica. Esta deducción no debe tomarse de forma rigurosa sino como un ejercicio de importancia histórica.
Supongamos ahora que la superficie rígida adopta la forma cilíndrica de radio r.

El cambio de velocidad en cada impacto Dv, es la diferencia entre la velocidad final v’ (en color azul) y la velocidad inicial v (en color rojo). La dirección de dicho cambio de velocidad Dv es radial y apunta hacia el centro de la trayectoria que describe la partícula. Su módulo vale

Esta misma expresión se puede deducir en el diagrama de velocidades, calculando el lado Dv del triángulo isósceles de vértice f que forman los vectores velocidad antes y después del impacto.
Después de n impactos contra la superficie rígida, la partícula describe una trayectoria que es un polígono regular de n lados. Teniendo en cuenta que el ángulo f =2p/n. El cambio total de velocidad que experimenta la partícula tras n impactos es

Calculamos ahora el tiempo que tarda la partícula en describir la trayectoria, un polígono regular de n lados.
En el triángulo isósceles formado por un lado y dos radios, calculamos el valor del lado, conociendo el ángulo f del vértice. La longitud del perímetro del polígono regular es

La partícula en cada impacto cambia la dirección de su velocidad pero no cambia su módulo. Por tanto, el tiempo que invierte en recorrer la trayectoria poligonal es P=l/v
El valor medio del módulo de la aceleración es


Cuando n es muy grande (tiende a infinito) el ángulo f es muy pequeño y podemos sustituir el seno por el ángulo. De modo que, el cambio total de velocidad que experimenta la partícula es

Cuando n es muy grande (tiende a infinito) el perímetro del polígono regular (trayectoria) que describe la partícula se aproxima a una circunferencia de radio r.
Como el módulo de la velocidad de la partícula v no cambia en los impactos con la pared rígida, el tiempo P que tarda en describir la circunferencia es

El módulo de la aceleración media es

Dada la simetría de la trayectoria circular, la aceleración media es la aceleración de la partícula en cada instante

La deducción de la fórmula de la aceleración normal se basa en el análisis de la trayectoria poligonal que sigue una partícula que choca contra una superficie cilíndrica. Esta deducción no debe tomarse de forma rigurosa sino como un ejercicio de importancia histórica.
Deducción de la formula de la aceleración normal por Newton
Como veremos en esta deducción, lo importante es el cambio en la dirección de la velocidad, no la causa que produce este cambio, ya sea el choque con la superficie rígida, la acción de la gravedad, etc.| Consideremos una partícula que se mueve en línea recta con velocidad constante v y que choca contra una superficie rígida. Como vemos en la figura, la componente de la velocidad v que es perpendicular a la superficiev·cosq cambia de sentido en el momento del impacto. Sin embargo, la componente que es paralela a la superficiev·senq no cambia durante el impacto.El cambio de velocidad que experimenta la partícula en el choque contra la superficie rígida es Dv=2vcosq |
El cambio de velocidad en cada impacto Dv, es la diferencia entre la velocidad final v’ (en color azul) y la velocidad inicial v (en color rojo). La dirección de dicho cambio de velocidad Dv es radial y apunta hacia el centro de la trayectoria que describe la partícula. Su módulo vale
Esta misma expresión se puede deducir en el diagrama de velocidades, calculando el lado Dv del triángulo isósceles de vértice f que forman los vectores velocidad antes y después del impacto.
La aceleración media para n impactos
La velocidad de la partícula es constante en los tramos rectos y por tanto, la aceleración es nula. Cuando choca con la superficie rígida la partícula cambia bruscamente la dirección de su velocidad aunque no su módulo y la aceleración en el instante del impacto es infinita. La aceleración media como veremos nos conduce a la fórmula de la aceleración normal.Después de n impactos contra la superficie rígida, la partícula describe una trayectoria que es un polígono regular de n lados. Teniendo en cuenta que el ángulo f =2p/n. El cambio total de velocidad que experimenta la partícula tras n impactos es
Calculamos ahora el tiempo que tarda la partícula en describir la trayectoria, un polígono regular de n lados.
En el triángulo isósceles formado por un lado y dos radios, calculamos el valor del lado, conociendo el ángulo f del vértice. La longitud del perímetro del polígono regular es
La partícula en cada impacto cambia la dirección de su velocidad pero no cambia su módulo. Por tanto, el tiempo que invierte en recorrer la trayectoria poligonal es P=l/v
El valor medio del módulo de la aceleración es
La aceleración media para infinitos impactos
El cambio total de velocidad que experimenta la partícula tras n impactos esCuando n es muy grande (tiende a infinito) el ángulo f es muy pequeño y podemos sustituir el seno por el ángulo. De modo que, el cambio total de velocidad que experimenta la partícula es
Cuando n es muy grande (tiende a infinito) el perímetro del polígono regular (trayectoria) que describe la partícula se aproxima a una circunferencia de radio r.
Como el módulo de la velocidad de la partícula v no cambia en los impactos con la pared rígida, el tiempo P que tarda en describir la circunferencia es
El módulo de la aceleración media es
Dada la simetría de la trayectoria circular, la aceleración media es la aceleración de la partícula en cada instante
En Física decimos que un cuerpo tiene aceleración cuando se produce un cambio del vector velocidad, ya sea en módulo o dirección. En apartados anteriores hemos visto que la aceleración se puede clasificar según el efecto que produce en la velocidad en aceleración tangencial (si hace que cambie el módulo del vector velocidad) y aceleración normal o centrípeta (si hace que cambie su dirección). Son las componentes intrínsecas de la aceleración. En este apartado vamos a desarrollar con mayor profundidad la aceleración centrípeta o normal.
Aceleración Centrípeta o Normal
La aceleración normal o centrípetamide los cambios de dirección de la velocidad en el tiempo. Su expresión viene dada por:
Donde:
a⃗ n : Es la aceleración normal o centrípeta del cuerpov : Es el módulo de la velocidad del cuerpo en el punto estudiadoρ : Es el radio de curvatura. En el caso de los movimiento circulares, coincide con el radio de giro del cuerpo.
La aceleración normal puede ser:
- =0: En los movimientos rectilíneos, donde la dirección permanece constante
- >0: En los movimientos curvilineos, donde la velocidad cambia continuamente de direccón
Observa que cualquier trayectoria que describa un cuerpo se puede considerar como una composición de trayectorias rectas y curvas. Las partes curvas de la trayectoria pueden a su vez considerarse arcos de circunferencia. La siguiente imagen ilustra este concepto

Como vemos, el centro de curvatura de un punto de la trayectoria curva es el centro de la circunferencia que pasa por él. El radio de dicha circunferencia es el radio de curvatura de dicho punto.
Demostración de la aceleración normal
Con anterioridad hemos visto que la aceleración instantánea es la derivada de la velocidad respecto al tiempo. Por otro lado, hemos visto que podemos expresar el vector velocidad como el producto de su módulo por unvector unitario tangente a la trayectoria: v⃗ =v⋅u⃗ t . Si desarrollamos estas dos ideas nos queda:
Donde hemos aplicado la regla de derivación de un producto D(ab)=a'b+ab'.
Vemos que el segundo término es el producto del módulo de la velocidad por la derivada de u⃗ t respecto al tiempo. Podemos demostrar que, en realidad, dicho vector es normal a la trayectoria:

- Expresamos
u⃗ t en función del ángulo genéricoθ - Aplicamos la regla de la cadena
- De lo anterior se deduce:
Deducción alternativa de las fórmulas de la aceleración tangencial y normal
Movimiento circular uniforme. Aceleración normal
Consideremos que una partícula describe un movimiento circular de radio r con velocidad constante v.La partícula se encuentra en la posición A en el instante t-Dt/2, y su velocidad (tangente a la trayectoria) es v1. La partícula se encuentra en la posición simétrica B en el instantet+Dt/2 y su velocidad es v2.
Coloquemos los dos vectores velocidad v1 y v2 que tienen la misma longitud v con vértice en el punto P y calculamos las componentes radial o normal y tangencial del vector diferencia Dv=v2-v1.
- Componente normal
(Dv)n=v2·senf -v1·sen(-f )=2v·senf
- Componente tangencial
(Dv)t=v2·cosf -v1·cos(-f )=0Por tanto el vector Dv es paralelo a la dirección radial PO, y está dirigido hacia el centro O.
Como la partícula recorre el arco AB de ángulo 2f con velocidad v constante.
El valor medio de la componente normal de la aceleración es por tanto,
La componente normal de la aceleración instantánea es el límite de la aceleración media cuando el intervalo de tiempo Dt® 0, o bien cuando f ® 0. En este límite, senf /f ® 1 y por tanto, la componente normal de la aceleración en el instante t o en el punto P es
Naturalmente, la componente tangencial de la aceleración es cero en dicho instante, at=0.
Movimiento circular no uniforme. Aceleración tangencial y normal
Supongamos que la partícula pasa por el punto A en el instante t-Dt1 y lleva una velocidad v1 (tangente a la trayectoria), y pasa por el punto simétrico B en el instante t-Dt2llevando una velocidad v2. Como el movimiento no es uniforme los módulos de las velocidades serán diferentes.Calculamos las componentes radial o normal y tangencial del vector diferencia Dv=v2-v1.
- Componente normal
(Dv)n=v2·senf -v1·sen(-f )=2(v2+v1)·senf
- Componente tangencial
(Dv)t=v2·cosf -v1·cos(-f )= (v2-v1) cosfAl no ser los vectores velocidad de igual módulo, el vector diferencia Dv y por tanto la aceleración no tienen en general, dirección radial.
La partícula recorre el arco AB de ángulo 2f empleando un tiempo Dt=Dt1+ Dt2. La velocidad media <v> de la partícula en este intervalo de tiempo es
La componente normal y tangencial de la aceleración serán por tanto,
En el límite cuando el intervalo de tiempo Dt® 0, o bien cuando f ® 0, se cumple que, senf / f ® 1, cosf ® 1. La velocidad media <v>® v es la velocidad en el instante tcuando el móvil pasa por P, y también la velocidad promedio (v1+v2)/2® v.
De este modo obtenemos la misma fórmula de la componente normal de la aceleración que en el apartado anterior.
En cuanto a la componente tangencial, el numerador es un cambio infinitesimal en el módulo de la velocidad dv y el denominador es el tiempo dt que tarda la partícula en efectuar dicho cambio.
Las componentes de la aceleración serán, por tanto,
Deducción alternativa de las fórmulas de la aceleración tangencial y normal
En la figura, la partícula se encuentra en el instante t en el punto P, formando un ángulo q con el eje X.
El vector posición r de la partícula es
r=xi+yj=r·cosq i+r·senq j
El vector velocidad v se obtiene derivando el vector posición respecto del tiempo
El vector aceleración se obtiene derivando el vector velocidad
El vector aceleración tiene dos componentes, que podemos expresar en virtud de las relaciones entre magnitudes angulares y lineales de dos formas.
La componente radial está dirigida hacia le centro de la circunferencia
an=w2r=v2/r,
La componente tangencial tiene la dirección de la velocidad, tangente a la trayectoria
at=a r=dv/dt.
Deducción alternativa de la aceleración normal (I)
Supongamos que el cuerpo describe un movimiento circular de radio r con velocidad constante v.
El vector velocidad v es tangente a la trayectoria y es perpendicular al vector posición r.
Las componentes rectangulares del vector velocidad v son
Como v/r es constante, las componentes del vector aceleración a son
El módulo de la aceleración a en el movimiento circular uniforme es
Su dirección es radial (la misma que el vector r) y su sentido es hacia el centro (de sentido contrario al vector r).
Deducción alternativa de la aceleración normal (II)
En esta sección, se describe la deducción más simple que se ha encontrado de la fórmula de la aceleración normal en un movimiento circular uniforme
El vector velocidad v se define
Su módulo para un movimiento circular uniforme es
Siendo P el periodo o tiempo que tarda en completar una vuelta
Su dirección es tangente a la trayectoria, es decir, perpendicular al vector r
El vector aceleración a se define
El vector aceleración a se obtiene a partir del vector velocidad v, de la misma manera que el vector velocidad v se obtiene a partir del vector posición r. Su módulo será, análogamente,
Su dirección es tangente a la circunferencia de radio v, es decir perpendicular al vector v. Como vemos en la figura, los vectores a y r tienen la misma dirección pero sentidos contrarios.
La cinemática es la parte de la mecánica clásica que estudia la descripción del movimiento de un cuerpo, sin atender a la causa que lo produce. Se limita esencialmente al cálculo de la trayectoria del cuerpo en función del tiempo. Para ello se debe utilizar un sistema de coordenadas, llamado sistema de referencia, constituido por tres ejes perpendiculares entre sí (ejes XYZ).
Trataremos en todo este tema el movimiento de objetos puntuales (sin dimensiones).
Definimos las magnitudes vectoriales vector posición, vector velocidad y vector aceleración, expresadas en componentes en función de los vectores unitarios de los ejes XYZ.
| vector posición | |
| vector velocidad | |
| vector aceleración |
Las unidades respectivas de las magnitudes anteriores en el Sistema Internacional son: m, m/s y m/s2
En la siguiente figura están respresentados dichos vectores en dos dimensiones.
| Es importante recordar que el vector velocidad es siempre tangente a la trayectoria. |
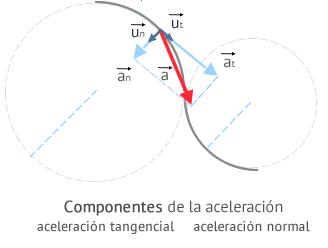
Componentes intrínsecas de la aceleración:
En algunas ocasiones conviene usar un sistema de referencia cuyos ejes sean en cada instante tangente y normal a la trayectoria (no son fijos).
Pincha sobre Tarzán y desplázalo de la posición de equilibrio, verás en la siguiente animación el movimiento oscilatorio de una masa y las componentes de su aceleración sobre el ejes tangente y el eje normal a la trayectoria.
Definimos las componentes intrínsecas de la aceleración (aceleración normal y aceleración tangencial) como las componentes de la aceleración sobre este sistema de referencia. Se puede demostrar que dichas componentes valen:
| aceleración tangencial | nula cuando el módulo de la velocidad es constante | |
| aceleración normal | nula cuando el movimiento es rectilíneo | |
A partir de las expresiones anteriores se puede deducir la interpretación física de cada una de estas componentes:
la aceleración normal da cuenta del cambio en la dirección del vector velocidad de la partícula en cada punto y la aceleración tangencial de la variación del módulo de dicho vector velocidad.
|
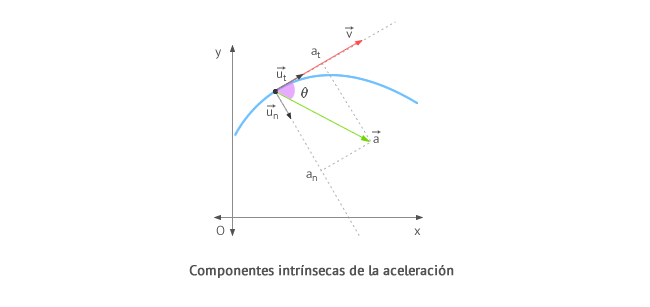
En la siguiente gráfica se han representado los vectores unitarios normal y tangente en dos puntos de la trayectoria y la descomposición del vector aceleración en sus componentes intrínsecas.
| vector unitario tangente | |||
| vector unitario normal | |||
| radio de curvatura | |||
No hay comentarios:
Publicar un comentario