Matemáticas - Teoría de grafos

camino hamiltoniano, en el campo matemático de la teoría de grafos, es un camino de un grafo, una sucesión de aristas adyacentes, que visita todos los vértices del grafo una sola vez. Si además el último vértice visitado es adyacente al primero, el camino es un ciclo hamiltoniano.

El problema de encontrar un ciclo (o camino) hamiltoniano en un grafo arbitrario se sabe que es NP-completo.

Los caminos y ciclos hamiltonianos se llaman así en honor de William Rowan Hamilton, inventor de un juego que consistía en encontrar un ciclo hamiltoniano en las aristas de un grafo de un dodecaedro. Hamilton resolvió este problema usandocuaterniones, aunque su solución no era generalizable a todos los grafos.

Ciclo hamiltoniano.

Definición

Un camino hamiltoniano es un camino que pasa por cada vértice exactamente una vez. Un grafo que contiene un camino hamiltoniano se denomina un ciclo hamiltoniano si es un ciclo que pasa por cada vértice exactamente una vez (excepto el vértice del que parte y al cual llega). Un grafo que contiene un ciclo hamiltoniano se dice grafo hamiltoniano.

Estos conceptos se pueden extender para los grafos dirigidos los cuales son igual a un carro.

Ejemplos

• Todos los grafos ciclos son hamiltonianos.
• Todos los sólidos platónicos, (tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.) considerados como grafos, son hamiltonianos.¹

Notas

Cualquier ciclo hamiltoniano puede ser convertido en un camino hamiltoniano si se elimina cualquiera de sus aristas, pero un camino hamiltoniano puede ser extendido en ciclo sólo si los vértices de los extremos son adyacentes.

Teorema de Bondy-Chvátal

La mejor caracterización de los grafos hamiltonianos fue dada en 1972 por el teorema de Bondy-Chvátal que generalizaba los resultados anteriormente encontrados porG. A. Dirac. Básicamente dice que un grafo es hamiltoniano si existen suficientes aristas. Primero debemos definir lo que es la cerradura de un grafo.

Dado un grafo G con n vértices, la cerradura (cl(G)) es construida de manera única a partir de G agregando toda arista u-v si el par no adyacente de vértices u y vcumple que grado(v) + grado(u) ≥ n

Un grafo es hamiltoniano si y sólo si su grafo cerradura es hamiltoniano. Bondy-Chvátal (1972)

Como todos los grafos completos son hamiltonianos, todos los grafos cuya cerradura sea completa son hamiltonianos. Este resultado se basa en los teoremas de Dirac y Ore.

Un grafo con n vértices (n > 3) es hamiltoniano si cada vértice tiene grado mayor o igual a n/2. Dirac (1952)

Un grafo con n vértices (n > 3) es hamiltoniano si la suma de los grados de 2 vértices no adyacentes es mayor o igual que n. Ore (1960)

Sin embargo, existe un resultado anterior a todos estos teoremas.

Un grafo con n vértices (n ≥ 2) es hamiltoniano si la suma de los grados de 2 vértices es mayor o igual que n-1. L.Redei (1934)

Como puede verse, este teorema pide más hipótesis que los anteriores ya que la propiedad de los grados debe cumplirse para todo vértice en el grafo.

 centralidad en un grafo se refiere a una medida posible de un vértice en dicho grafo, que determina su importancia relativa dentro de éste.¹

Poder reconocer la centralidad de un nodo puede ayudar a determinar, por ejemplo, el impacto de una persona involucrada en una red social, la relevancia de una habitación en un edificio representado en sintaxis del espacio, la importancia de una carretera en una red urbana, o los componentes esenciales de una red de computadoras.

El concepto fue introducido inicialmente por Bavelas a fines de los años 1940.² Es uno de los conceptos más estudiados en el análisis de redes y desde finales de los años 70 en el análisis de redes sociales,^3 4 y muchos de los conceptos relacionados con las medidas de centralidad reflejan su origen sociológico.⁵

La centralidad no es un atributo intrínseco de los nodos o actores de una red, como podrían serlo la autoestima, la temperatura, el ingreso monetario, etc. sino un atributo estructural, es decir, un valor asignado que depende estrictamente de su localización en la red. La centralidad mide según un cierto criterio la contribución de un nodo según su ubicación en la red, independientemente de si se esté evaluando su importancia, influencia, relevancia o prominencia.

Por ejemplo, de acuerdo con una medida de centralidad razonable, en un grafo estrella el nodo central debería ocupar un valor máximo de centralidad, mientras que los nodos de las puntas ocuparían un valor de centralidad inferior.

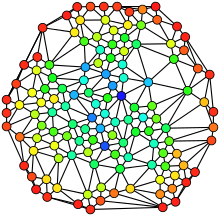
Ejemplos de un mismo grafo donde se visualizan distintas medidas de centralidad:
A) intermediación
B) cercanía
C) valor propio
D) grado
E) centralidad armónica
F) centralidad de Katz.
Las tonalidades van del rojo (más centrales) al azul (más periféricos).

Medidas de centralidad

Las medidas de centralidad se pueden agrupar en dos categorías: medidas radiales («radial measures») y mediales («medial measures»).⁶ Las primeras toman como punto de referencia un nodo dado que inicia o termina recorridos por la red, mientras que las segundas toman como referencia los recorridos que pasan a través de un nodo dado.⁷ Las medidas radiales a su vez se pueden clasificar en medidas de volumen y de longitud, según el tipo de recorridos que consideran. Las primeras miden el volumen (o el número) de recorridos limitados a dicha longitud prefijada, en tanto que las segundas miden la longitud de los recorridos necesarios para alcanzar un volumen prefijado.⁷

Desde la formulación realizada por Bavelas,² se han propuesto diversas medidas de centralidad de un nodo. Existen cuatro de estas medidas que son ampliamente usadas en análisis de redes:

• La centralidad de grado («degree centrality»)
• La cercanía («closeness»)
• La intermediación («betweenness»)
• La centralidad de vector propio («eigenvector centrality»).

La primera y la última son medidas radiales de volumen. La segunda es una medida radial de longitud, y la tercera una medida medial.⁷ Para algunas de estas medidas existen a su vez versiones más generales o bien generalizaciones para las redes con pesos.⁸

Adicionalmente, se puede distinguir entre las medidas «absolutas» de centralidad, que indican un valor no comparable y aquellas que están normalizadas, denominadas medidas «relativas» de centralidad.

Centralidad de grado

La centralidad de grado («degree centrality») es la primera y más simple de las medidas de centralidad.⁷ Corresponde al número de enlaces que posee un nodo con los demás.

Formalmente, dado un grafo ${\displaystyle G:=(V,E)}$, donde ${\displaystyle V}$ es su conjunto de vértices y ${\displaystyle E}$ su conjunto de aristas, entonces para cada nodo ${\displaystyle v\in V}$ su centralidad de grado ${\displaystyle C_{DEG}(v)}$ se define como:⁷

${\displaystyle C_{DEG}(v)={\mbox{grado}}(v)}$

Si se tiene la matriz de adyacencia del grafo, donde cada posición ${\displaystyle a_{ij}}$ asume el valor 1, si existe la arista ${\displaystyle (i,j)}$ y el valor 0, si no existe, entonces la centralidad de grado de cada nodo ${\displaystyle j}$ se puede definir como:

${\displaystyle C_{DEG}(j)=\sum _{i}a_{ij}}$

Para grafos dirigidos, se pueden definir dos medidas de centralidad de grado diferentes, correspondientes al grado de entrada o el de salida. En el sentido de relaciones interpersonales, el primero puede interpretarse como una medida de popularidad, mientras que el segundo como una de sociabilidad.

Dos criterios para normalizar esta medida pueden ser dividir el grado de cada nodo por el máximo grado obtenido de la red, o bien dividirlo por el número total de nodos de la red.

Las interpretaciones de esta medida pueden ser múltiples. En una red social, puede ser el número de amistades o conexiones que posee cada persona, en cuyo caso cuantifica la conectividad o popularidad en la red. En una red de infección puede medir el grado de riesgo de ser contagiado o el índice de exposición. En la propagación de un rumor, puede medir la probabilidad de obtener la información a través de un rumor.

En complejidad computacional, el cálculo de esta medida toma ${\displaystyle \Theta (V^{2})}$ en una matriz de adyacencia densa, y ${\displaystyle \Theta (E)}$ en una matriz dispersa.

Centralidad de camino-K

El grado de un nodo puede verse como el número de caminos de longitud 1 que lo conectan con otros nodos. Una generalización natural a la centralidad de grado, es lacentralidad de camino-K («K-path centrality») que para cada nodo mide el número de caminos de largo a lo más ${\displaystyle k}$ que lo conectan otros nodos.⁷

Centralidades de Katz y Bonacich

Otra generalización de la centralidad de grado es la centralidad de Katz,⁹ que para un nodo cuenta el número de todos los otros nodos que están conectados con él a través de un camino, al mismo tiempo que se penalizan las conexiones con nodos más distantes por medio de un factor ${\displaystyle \beta \in (0,1)}$.

Formalmente, sea ${\displaystyle A}$ la matriz de adyacencia del grafo, y ${\displaystyle n}$ el número total de nodos, la centralidad de Katz ${\displaystyle C_{KATZ}(i)}$ de un nodo ${\displaystyle i}$ se define como:⁷

${\displaystyle C_{\mathrm {Katz} }(i)=\sum _{k=1}^{\infty }\sum _{j=1}^{n}\alpha ^{k}(A^{k})_{ji}}$

donde ${\displaystyle e_{i}^{T}}$ es un vector fila cuyo ${\displaystyle i}$-ésimo elemento es 1 y el resto son 0, y 1 es un vector de puros unos. Como se verá más adelante, esta medida está relacionada con lacentralidad de vector propio.⁷

Una pequeña variación de la centralidad de Katz está dada por la centralidad de Bonacich,¹⁰ la cual permite valores negativos para el factor ${\displaystyle \beta }$:

${\displaystyle C_{BON}(i)=e_{i}^{T}({\frac {1}{\beta }}\sum _{k=1}^{\infty }(\beta A)^{k}){\mathbf {1} }={\frac {1}{\beta }}\sum _{k=1}^{\infty }\sum _{j=1}^{n}\beta ^{k}(A^{k})_{ij}}$

De este modo el peso negativo permite restar los caminos de número par de los de número impar, lo cual es interpretable en redes de intercambio.^7 6

Centralidad de Hubbell

Una generalización que incluye a las centralidades de Katz y Bonacich es la centralidad de Hubbell,¹¹ definida formalmente como:

${\displaystyle C_{HUB}(i)=e_{i}^{T}(\sum _{k=0}^{\infty }X^{j}){\mathbf {y} }}$

donde ${\displaystyle X}$ es una matriz e ${\displaystyle {\mathbf {y} }}$ un vector. Si ${\displaystyle X=\beta A}$ y ${\displaystyle {\mathbf {y} }=\beta A{\mathbf {1} }}$ se obtiene la centralidad de Katz, y si ${\displaystyle X=\beta A}$ y ${\displaystyle {\mathbf {y} }=A{\mathbf {1} }}$, se obtiene la centralidad de Bonacich.⁷

Cercanía

La medida de cercanía, definida por el matemático Murray Beauchamp en 1965¹² y luego popularizada por Freeman en 1979,³ es la más conocida y utilizada de las medidas radiales de longitud. Se basa en calcular la suma o bien el promedio de las distancias más cortas desde un nodo hacia todos los demás.⁷

Formalmente, la cercanía ${\displaystyle C_{CLO}(i)}$ de un nodo ${\displaystyle i}$ se define como:

${\displaystyle C_{CLO}(i)=e_{i}^{T}S{\mathbf {1} }=\sum _{j=1}^{n}(S)_{ij}}$

donde ${\displaystyle S}$ es la matriz de distancias de la red, es decir, aquella matriz cuyos elementos ${\displaystyle (i,j)}$ corresponden a la distancia más corta desde el nodo ${\displaystyle i}$ hasta el nodo ${\displaystyle j}$. Mientras menor sea el valor anterior, se puede decir que el nodo está más «cercano» al centro de la red. En tal caso definido así corresponde en realidad a una medida de lejanía. Por la misma razón, a veces la cercanía se define más bien como el valor recíproco de lo anterior, no cambiando por ello la idea del concepto.¹³

${\displaystyle C_{CLO}(i)={\frac {1}{e_{i}^{T}S{\mathbf {1} }}}={\frac {1}{\sum _{j=1}^{n}(S)_{ij}}}}$

En una red de flujo esta medida se puede interpretar como el tiempo de llegada a destino de algo que fluye a través de la red.¹ También puede interpretarse como la rapidez que tomará la propagación de la información desde un nodo a todos los demás.¹⁴ La cercanía mide de alguna forma la accesibilidad de un nodo en la red. Este concepto es utilizado también de manera similar en topología (donde se define como un espacio métrico) y en teoría de grafos, donde se aplica entre otros campos alanálisis de redes.

Variantes de cercanía

La medida tradicional de cercanía asume que la propagación de información siempre se da en la red a través del camino más corto. Este modelo puede no ser el más realista para algunos tipos de escenarios de comunicación. Por ello han surgido algunas variantes de esta medida.

Una de ellas es la denominada cercanía por camino aleatorio («random-walk closeness centrality») introducida por Noh y Rieger en 2003 y que considera recorridos aleatorios para acceder de un nodo a los demás, en lugar de escoger siempre el camino más corto.¹⁵

Varios años antes, en 1989, Stephenson y Zelen definieron una variante de medida de centralidad enfocada en el traspaso de información («information centrality») en una red. Esta medida determina la longitud media armónica de los caminos que acaban en un nodo ${\displaystyle i}$, la que será pequeña si ${\displaystyle i}$ se conecta con muchos otros nodos a través de caminos cortos.¹⁶

En 2006, Dangalchev modifica la definición de cercanía para medir la vulnerabilidad en las redes, permitiendo analizar grafos desconectados (en la definición original, los nodos aislados del grafo tendrían una cercanía igual a cero):¹⁷

${\displaystyle C_{DCLO}(i)=\sum _{j=1}^{n}2^{-(S)_{ij}}}$

En 2010 Opsahl propuso otra extensión de la medida para redes con componentes desconectadas.¹⁸

Intermediación

Las tonalidades que van desde el rojo (valor 0) hasta el azul (valor máximo) indican la intermediación de los nodos en el grafo.

La intermediación («betweenness centrality») es una medida que cuantifica la frecuencia o el número de veces que un nodo actúa como un puente a lo largo del camino más corto entre otros dos nodos.⁷

La medida fue introducida por Linton Freeman en 1977, como forma de cuantificar el control de un humano en la comunicación existente con otros humanos en una red social. La idea intuitiva es que si se eligen dos nodos al azar, y luego también al azar uno de los eventuales posibles caminos más cortos entre ellos, entonces los nodos con mayor intermediación serán aquellos que aparezcan con mayor probabilidad dentro de este camino.¹⁹

Formalmente, la intermediación ${\displaystyle C_{BET}(i)}$ de un nodo ${\displaystyle i}$ en una red se define como:⁷

${\displaystyle C_{BET}(i)=\sum _{j,k}{\frac {b_{jik}}{b_{jk}}}}$

donde ${\displaystyle b_{jk}}$ es el número de caminos más cortos desde el nodo ${\displaystyle j}$ hasta el nodo ${\displaystyle k}$, y ${\displaystyle b_{jik}}$ el número de caminos más cortos desde ${\displaystyle j}$hasta ${\displaystyle k}$ que pasan a través del nodo ${\displaystyle i}$.

En complejidad computacional, determinar el camino más corto para cada par de nodos de un grafo ${\displaystyle G=(V,E)}$ puede calcularse en tiempo ${\displaystyle \Theta (V^{3})}$ (por ejemplo usando el algoritmo de Floyd-Warshall) y utilizando un espacio ${\displaystyle \Theta (V^{2})}$.⁷ En un grafo disperso, el algoritmo de Johnsonpuede lograr lo mismo en tiempo ${\displaystyle O(V^{2}\log V+VE)}$, y si el grafo es sin pesos, se puede lograr en tiempo ${\displaystyle O(VE)}$ y espacio ${\displaystyle O(|V|+|E|)}$ utilizando el algoritmo de Brandes.²⁰

Los nodos con una alta intermediación, al igual que las aristas con una alta intermediación en los lazos interpersonales (tema que no tiene que ver directamente con centralidad y que no abordaremos aquí), suelen jugar un rol crítico en la estructura de la red, cuando hay grandes flujos de información que son transportados por nodos pertenecientes a grupos compactos. En una red social están relacionados con los agujeros estructurales («structural holes»), es decir, con aquellos nodos de los que depende la integración de algunas componentes de la red.⁷ Los nodos que poseen una posición de intermediarios de alguna manera son también controladores o reguladores del flujo de información. Así, en un proceso de difusión, si el valor de intermediación de un nodo es alto entonces puede actuar como un broker; y si es suficientemente alto como para controlar el flujo de información, entonces puede actuar como un guardián.

Intermediación de Newman

Newman propuso en 2005¹⁴ una versión alternativa de la medida de intermediación, basada en considerar caminos aleatorios del grafo, y no exclusivamente los más cortos. La idea es tomar en cuenta todos los caminos posibles, y calcular la medida de acuerdo a los elegidos aleatoriamente. Formalmente se define como:⁷

${\displaystyle C_{NBET}(i)=\sum _{j\neq i\neq k}R_{jk}^{(i)}}$

donde ${\displaystyle R^{(i)}}$ es la matriz cuyos elementos ${\displaystyle (j,k)}$ contienen la probabilidad de ocurrencia de un camino al azar desde ${\displaystyle j}$ hasta ${\displaystyle k}$ y que contiene al nodo ${\displaystyle i}$ como nodo intermediario.

Centralidad de vector propio

La centralidad de vector propio mide la influencia de un nodo en una red. Fue propuesta por Phillip Bonacich en 1972,²¹ y corresponde al principal vector propio de la matriz de adyacencia del grafo analizado.⁷

Intuitivamente, los nodos que poseen un valor alto de esta medida de centralidad están conectados a muchos nodos que a su vez están bien conectados, también en este sentido; por lo tanto, son buenos candidatos para difundir información, divulgar rumores o enfermedades, etc. Los nodos más centrales en este sentido corresponden a centros de grandes grupos cohesivos. Mientras que en el caso de la centralidad de grado, cada nodo pesa lo mismo dentro de la red, en este caso la conexión de los nodos pesa de forma diferente.

El cálculo del PageRank de Google, utilizado para medir la relevancia de páginas web en Internet, es una variante de esta medida.²² Otra medida muy relacionada con esta es la centralidad de Katz, debido a que la centralidad de vector propio es el límite de la centralidad de Katz cuando el factor ${\displaystyle \beta }$ se aproxima a ${\displaystyle {\frac {1}{\lambda }}}$ por debajo,^7 6donde ${\displaystyle \lambda }$ es el valor propio obtenido de la ecuación ${\displaystyle Ax=\lambda x}$.

En general habrá varios valores propios para los cuales existe una solución de vector propio. Sin embargo, el requerimiento adicional de que las entradas de los vectores propios sean positivos implica (por el Teorema de Perron-Frobenius) que sólo los mayores valores propios conduzcan a la medida de centralidad deseada.²³ El método de las potencias es uno de los muchos algoritmos existentes para calcular el valor propio que puede ser utilizado para encontrar el vector propio dominante.²² Además, este puede generalizarse tal que las entradas en la matriz de adyacencia ${\displaystyle A}$ puedan ser números reales representrando fuerzas de conexión, como en una matriz estocástica.

Centralidad de Contribución (o basada en disimilaridades)

Esta es una metodología relacionada con el uso de medidas de disimilaridad (propias de la teoría de clasificación y de la minería de datos) a fin de retro-alimentar medidas de centralidad ya existentes en redes complejas. En ²⁴ se ilustra la metodología usando autocentralidad (o centralidad de vector propio), calculando la centralidad de cada nodo a través de la solución del problema de autovectores:

${\displaystyle W\mathbf {c} =\lambda _{\text{máx}}\mathbf {c} }$

donde ${\displaystyle W_{ij}=A_{ij}D_{ij}}$ (producto coordenada a coordenada) y ${\displaystyle D_{ij}}$ es una matriz de disimilaridades arbitraria, definida a través de una medida de disimilaridad, e.g. la disimilaridad de Jaccard:

${\displaystyle D_{ij}=1-{\dfrac {|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|}}}$

donde esta medida nos permite cuantificar la contribución topológica de cada nodo (que es la razón por la que estas medidas son llamadas centralidades de contribución) en una red dada, teniendo más peso/relevancia aquellos nodos con mayor disimilaridad, puesto que estos permiten a un nodo dado acceder a aquellos nodos a los que no pueden acceder directamente.

Cabe destacar que ${\displaystyle W}$ es no-negativa puesto que ${\displaystyle A}$ y ${\displaystyle D}$ son no-negativas, de manera que podemos aplicar el teorema de Perron Frobenius para asegurar que el problema de autovectores anterior tiene una única solución no-negativa para ${\displaystyle \lambda =\lambda _{\text{máx}}}$, permitiéndonos inferir la centralidad de cada nodo en la red. Por lo tanto, la centralidad del i-ésimo nodo estará dada por

${\displaystyle c_{i}={\dfrac {1}{n}}\sum _{j=1}^{n}W_{ij}c_{j},\,\,\,\,\,\,j=1,\cdots ,n}$

donde ${\displaystyle n}$ es el número de nodos en la red. Varias redes y medidas de disimilaridad han sido probadas²⁵ , obteniéndose en todos los casos excelentes resultados.

Centralidad alfa

La centralidad alfa es una variante de la centralidad de vector propio en que los nodos están sujetos a distinta importancia dependiendo de factores externos. Esta medida fue definida por Bonacich y Lloyd en 2001.²⁶

Esta medida está implementada en la biblioteca de un software de análisis de redes sociales denominado «igraph», y se utiliza para especificar la importancia relativa de factores endógenos vs. exógenos en una determinación de centralidad al momento de analizar o visualizar una red.