Epónimos relacionados con la física

ecuaciones epónimas de la física

ecuación de Eyring también conocida como ecuación de Eyring–Polanyi en Cinética química relaciona la velocidad de reaccióncon la temperatura. Fue desarrollada casi simultáneamente en 1935 por Henry Eyring, M.G. Évans y Michael Polanyi. Esta ecuación es parte de la teoría del estado de transición (o bien, teoría del complejo activado) y equivale de modo trivial a la ecuación de Arrheniusobtenida empíricamente; ambas ecuaciones pueden derivarse fácilmente de la termodinámica estadística en la teoría cinética de gases.¹

La forma de la ecuación de Eyring–Polanyi recuerda algo a la ecuación de Arrhenius:

${\displaystyle \ k={\frac {k_{\mathrm {B} }T}{h}}\mathrm {e} ^{-{\frac {\Delta G^{\ddagger }}{RT}}}}$

donde:

• ΔG^‡ es la energía libre de activación,
• k_B es la constante de Boltzmann, y
• h es la constante de Planck.

Puede reescribirse como:

${\displaystyle k=\left({\frac {k_{\mathrm {B} }T}{h}}\right)\mathrm {exp} \left({\frac {\Delta S^{\ddagger }}{R}}\right)\mathrm {exp} \left(-{\frac {\Delta H^{\ddagger }}{RT}}\right)}$

Para encontrar la forma lineal de la ecuación de Eyring–Polanyi se parte de:

${\displaystyle \ln {\frac {k}{T}}={\frac {-\Delta H^{\ddagger }}{R}}\cdot {\frac {1}{T}}+\ln {\frac {k_{\mathrm {B} }}{h}}+{\frac {\Delta S^{\ddagger }}{R}}}$

donde:

• ${\displaystyle \ k}$ es la constante de velocidad de la ecuación de velocidad,
• ${\displaystyle \ T}$ es la temperatura absoluta,
• ${\displaystyle \ \Delta H^{\ddagger }}$ es la entalpía de activación,
• ${\displaystyle \ R}$ es la constante de los gases ideales,
• ${\displaystyle \ k_{\mathrm {B} }}$ es la constante de Boltzmann,
• ${\displaystyle \ h}$ es la constante de Planck,
• ${\displaystyle \ \Delta S^{\ddagger }}$ es la entropía de activación.

Una cierta reacción química tiene lugar a diferentes temperaturas y se determinan las velocidades de reacción. La gráfica de ${\displaystyle \ \ln(k/T)}$versus ${\displaystyle \ 1/T}$ da una línea recta con pendiente ${\displaystyle \ -\Delta H^{\ddagger }/R}$ de la cual puede derivarse la entalpía de activación y de la ordenada en el origen o punto de corte con el eje de ordenadas ${\displaystyle \ \ln(k_{\mathrm {B} }/h)+\Delta S^{\ddagger }/R}$ se deriva la entropía de activación.

La ecuación de Eyring, así como la de Arrhenius, describen la relación entre temperatura y velocidad de reacción. Estrictamente hablando, la ecuación de Arrhenius sólo puede ser aplicada a la cinética de reacciones en gases.

En cambio la ecuación de Eyring es usada también en el estudio de reacciones en soluciones y otros casos donde el modelo de colisión simple no es de gran ayuda.

La ecuación de Arrhenius está basada en la observación empírica que relaciona la temperatura con la velocidad de una reacción, mientras que la ecuación de Eyring es una construcción teórica, basada en el modelo de estado de transición.

Supongamos una reacción entre dos moléculas A y B, que reaccionan para obtener un producto C:

La velocidad de reacción estará dada por la siguiente ecuación:

Tomando en cuenta la teoría de  transición de estado, A y B  se encontrarán en un estado de transición  inestable ( AB ‡) , antes de convertirse en C.

Existe una “barrera de energía” en el camino entre los reactantes A y B y el producto C. Esta barrera determina un mínimo de energía necesaria para que la reacción pueda ocurrir. Esta energía es llamada entalpía de activación.

Como se observa en la gráfica de arriba, al principio de la reacción A y B se encuentran separados pero acercándose. Si las moléculas tienen suficiente energía la reacción comenzará. El estado de máxima energía en la reacción es en el estado de transición, cuando A y B se hallan formando el estado de transición inestable ( AB ‡). Luego, la gráfica baja a niveles bajos de energía, cuando se produce C.

La velocidad de esta reacción también depende de las concentraciones de A y B, por lo tanto, esta velocidad sería descrita con la siguiente ecuación:

k‡ es una constante de estadística termodinámica, conocida  como constante del estado de transición:

kB =  Constante de Boltzmann [ 1.381 · 10 -23 J · K -1 ]
T  =  temperatura absoluta en grados Kelvin [ K ]
h  =  Constante de Planck [ 6.626 · 10 -34 J · s ]
Además, la concentración del estado de transición  [ AB ‡ ] se puede relacionar con las concentraciones de los reactivos A y B ( que se encuentran en seudoequilibrio) mediante la ley de acción de masas

K ‡ =  constante de equilibrio termodinámico

Sustituyendo k‡ y [ AB ‡ ] en la ecuación 4, por las ecuaciones 5 y 6 tenemos que:

Observando la ecuación 2, podemos combinarla con la ecuación 7, y obtenemos como resultado la constante k para toda la reacción:

Existe otra expresión para la constante  K‡, según la ley de van´t Hoff:

ΔG ‡ es la energía libre de activación, también descrita en función de entropía de activación, entalpía de activación y temperatura:

R  =  constante universal de los gases=   8.3145 [ J · mol -1 · K -1 ]

ΔG ‡ =  energía libre de activación [ kJ · mol -1 ]
ΔS ‡ =  entropía de activación [ J · mol -1 · K -1 ]
ΔH ‡ =  entalpía de activación [ kJ · mol -1 ]
Combinando las expresiones 9 y 10 y despejando lnK obtenemos:

La ecuación de Eyring  resulta  de la sustitución  de lnK en la ecuación 11 , por la ecuación 8.

La forma lineal de la ecuación de Eyring sería entonces:

 ecuación de Fokker–Planck es una ecuación diferencial parcial que describe la evolución temporal de la función de densidad de probabilidad de la velocidad de una partícula bajo la influencia de fuerzas de arrastre y fuerzas aleatorias, como en el movimiento browniano. La ecuación también puede generalizarse a otro tipo de variables.¹ La ecuación se aplica a sistemas que pueden ser descritos por un pequeño número de "macrovariables", donde otros parámetros varían tan rápidamente con el tiempo que pueden ser tratados como "ruido" o una perturbación.

Fue nombrada en reconocimiento de Adriaan Fokker² y Max Planck,³ y también es conocida como ecuación avanzada de Kolmogórov (difusión) (por Andréi Kolmogórov, que la introdujo por primera vez en un artículo de 1931⁴ ). Cuando se aplica a distribuciones de posición de partículas, es más conocida como ecuación de Smoluchowski. El caso de la difusión cero es conocido en mecánica estadística como ecuación de Liouville.

La primera derivación consistente de la ecuación de Fokker-Planck en el esquema sencillo de la mecánica clásica y cuántica fue realizado⁵ por los soviéticos Nikolay Bogoliubov y Nikolay Krylov.

Historia

El primer uso de la ecuación de Fokker-Planck fue la descripción estadística del movimiento browniano de una partícula en el seno de un fluido. El movimiento browniano sigue la ecuación de Langevin, que puede resolverse para diferentes perturbaciones estocásticas, mediante resultados promediados. Sin embargo, como alternativa a este procedimiento, puede usarse la ecuación de Fokker-Planck y considerar una densidad de probabilidad en la velocidad y el tiempo, ${\displaystyle f(\mathbf {v} ,t)}$. Esta distribución de probabilidad dependiente del tiempo puede aún depender de un conjunto de N macrovariables ${\displaystyle \ x_{i}}$, de tal manera que el movimiento browniano en cuestión puede ser representado por una ecuación de Fokker-Planck de la forma:

${\displaystyle {\frac {\partial f}{\partial t}}=-\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}\left[D_{i}^{1}(x_{1},\ldots ,x_{N})f\right]+\sum _{i=1}^{N}\sum _{j=1}^{N}{\frac {\partial ^{2}}{\partial x_{i}\,\partial x_{j}}}\left[D_{ij}^{2}(x_{1},\ldots ,x_{N})f\right],}$

donde:

• ${\displaystyle D^{1}}$ es el término de arrastre, que viene dado por un vector, y
• ${\displaystyle D^{2}}$ es el término difusivo, que viene dado por una matriz.

Relación con las ecuaciones diferenciales estocásticas

Véase también: ecuación diferencial estocástica

Dos soluciones estocásticas de la ecuación diferencial estocástica lineal de Itō, con diferentes parámetros: la línea azul presenta un arrastre mayor, mientras que la línea verde presenta una mayor varianza.

La ecuación de Fokker–Planck puede usarse para calcular la densidad de probabilidad asociada a una ecuación diferencial estocástica. Por ejemplo, a la ecuación diferencial de Itō:

${\displaystyle \mathrm {d} \mathbf {X} _{t}={\boldsymbol {\mu }}(\mathbf {X} _{t},t)\,\mathrm {d} t+{\boldsymbol {\sigma }}(\mathbf {X} _{t},t)\,\mathrm {d} \mathbf {W} _{t},}$

donde:

• ${\displaystyle \mathbf {X} _{t}\in \mathbb {R} ^{N}}$ es el estado del sistema y
• ${\displaystyle \mathbf {W} _{t}\in \mathbb {R} ^{M}}$ caracteriza un proceso de Wiener estándar M-dimensional.

Si la distribución inicial viene dada por ${\displaystyle \mathbf {X} _{0}\sim f(\mathbf {x} ,0)}$, entonces la densidad de probabilidad ${\displaystyle f(\mathbf {x} ,t)}$del estado ${\displaystyle \mathbf {X} _{t}}$ viene dada por la ecuación de Fokker–Planck con el término de arrastre y el término de difusión dados por:

${\displaystyle D_{i}^{1}(\mathbf {x} ,t)=\mu _{i}(\mathbf {x} ,t)\qquad D_{ij}^{2}(\mathbf {x} ,t)={\frac {1}{2}}\sum _{k}\sigma _{ik}(\mathbf {x} ,t)\sigma _{kj}^{\mathsf {T}}(\mathbf {x} ,t).}$

Ejemplos

Un proceso de Wiener escalar generado por la ecuación diferencia estocástica:

${\displaystyle \ \mathrm {d} X_{t}=\mathrm {d} W_{t}.}$

que tiene un término de arrastre nulo, un término y una matriz de difusión dada por el coeficiente 1/2, tiene una densidad de probabilidad dada por la siguiente ecuación de Fokker-Planck:

${\displaystyle {\frac {\partial f(x,t)}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}f(x,t)}{\partial x^{2}}}}$

que resulta ser precisamente la forma más sencilla posible de la ley de Fick para la difusión.

ecuaciones de Fresnel, también conocidas como fórmulas de Fresnel, son un conjunto de relaciones matemáticas que relacionan las amplitudes de las ondas reflejadas y refractadas (o transmitidas) en función de la amplitud de la onda incidente. Su nombre hace honor al físico francés Augustin-Jean Fresnel, quien estudió el comportamiento de la luz al desplazarse entre medios que tienen índices de refracción distintos.

Transmisión parcial y reflexión parcial de una onda unidimensional proveniente de un medio con índice de refracción menor que el del medio al que se transmite (nótese que al reflejarse cambia de fase).

Generalidades

Onda incidente que se transmite y que se refleja.

Cuando una onda electromagnética que se desplaza por un medio caracterizado por un índice de refracción ${\displaystyle \ n_{1}}$, incide sobre la interfaz con otro medio que posee un índice de refracción ${\displaystyle \ n_{2}}$, una parte de la onda se refleja y otra porción se transmite al otro medio. Las fórmulas de Fresnel dan una descripción completa y detallada del comportamiento de la onda, tanto en la onda que se refleja como en la onda que se transmite al segundo medio. La dirección de propagación de una onda electromagnética es siempre perpendicular a sus vectores eléctricos y magnéticos, por lo que uno de estos vectores debe estar en el plano de incidencia. Consideraremos que la onda electromagnética está polarizada elípticamente, ésta siempre va a poder expresarse mediante dos vectores perpendiculares en el plano de incidencia. Llamaremos al vector paralelo al plano de incidencia como ${\displaystyle \ {\vec {E_{\parallel }}}}$y al vector perpendicular a éste plano como ${\displaystyle {\vec {E_{\perp }}}}$. Simplificando el problema, sin perder generalidad, podemos describir a estos vectores así:

(1)${\displaystyle E_{\parallel }=A_{\parallel }\exp(-i\tau _{i})}$

donde ${\displaystyle A_{\parallel }}$ es la amplitud de la onda de incidencia paralela al plano incidente y ${\displaystyle \ \tau _{i}}$ viene dado por la expresión: ${\displaystyle \tau _{i}=wt-n{\vec {r}}\cdot {\vec {s^{i}}}}$ donde ${\displaystyle {\vec {s^{i}}}}$ es el unitario de la dirección.

(2)${\displaystyle {\vec {H}}=n{\vec {s}}\times {\vec {E}}}$

que nos da la dirección del campo magnético.

Relaciones

En el diagrama, un rayo de luz incidente PO incide en un punto O de la interfaz entre dos medios de índices de refracción n₁ y n₂. Parte del rayo se refleja formando el rayo OQ y otra parte se refracta formando el rayo OS. Los ángulos que los rayos incidente, reflejado y refractado forman con la normal a la interfaz son θ_i, θ_r y θ_t, respectivamente. La relación entre estos ángulos queda determinada por la ley de reflexión y la ley de Snell.

La fracción de la intensidad de la luz incidente que es reflejada en la interfaz es determinada por el coeficiente de reflexión R, y la fracción refractada es determinada mediante el coeficiente de transmisión T. Las ecuaciones de Fresnel asumen que los dos materiales son paramagnéticos, es decir, poseen una permeabilidad magnética similar a la del vacío. De esta forma, las ecuaciones se pueden usar para calcular R y T.

Figura 1: Polarización s de las ondas incidida, refractada y reflejada con diferentes índices de refracción de los medios.

El cálculo de R y T depende de la polarización del rayo incidente.

Figura 2: Polarización p de las ondas incidida, refractada y reflejada.

Onda polarizada

- Si la luz está polarizada en la dirección del campo eléctrico, perpendicular al plano del diagrama, polarizada en s(ver figura 1), el coeficiente de la reflexión viene dado por:

${\displaystyle {{R}_{S}}={{\left[{\frac {\operatorname {sen}({{\theta }_{t}}-{{\theta }_{i}})}{\operatorname {sen}({{\theta }_{t}}+{{\theta }_{i}})}}\right]}^{2}}={{\left[{\frac {{{n}_{1}}\cos {{\theta }_{i}}-{{n}_{2}}\cos {{\theta }_{t}}}{{{n}_{1}}\cos {{\theta }_{i}}+{{n}_{2}}\cos {{\theta }_{t}}}}\right]}^{2}}}$

Donde θt se obtiene de θi por la Ley de Snell

- Si el rayo está polarizado en paralelo al plano del diagrama, polarizado en p (ver figura 2), R viene dado por:

${\displaystyle {{R}_{P}}={{\left[{\frac {\tan({{\theta }_{t}}-{{\theta }_{i}})}{\tan({{\theta }_{t}}+{{\theta }_{i}})}}\right]}^{2}}={{\left[{\frac {{{n}_{1}}\cos {{\theta }_{t}}-{{n}_{2}}\cos {{\theta }_{i}}}{{{n}_{1}}\cos {{\theta }_{t}}+{{n}_{2}}\cos {{\theta }_{i}}}}\right]}^{2}}}$

EL coeficiente de transmisión en cada caso está dado por:

${\displaystyle {\begin{aligned}&{{T}_{S}}=1-{{R}_{S}}\\&{{T}_{P}}=1-{{R}_{P}}\\\end{aligned}}}$

Onda no polarizada

Si la luz no está polarizada, el coeficiente de reflexión es:

${\displaystyle R={\frac {({{R}_{S}}+{{R}_{P}})}{2}}}$

Los coeficientes de reflexión y transmisión representan los ratios de intensidad incidente que se reflejan y transmiten respectivamente.

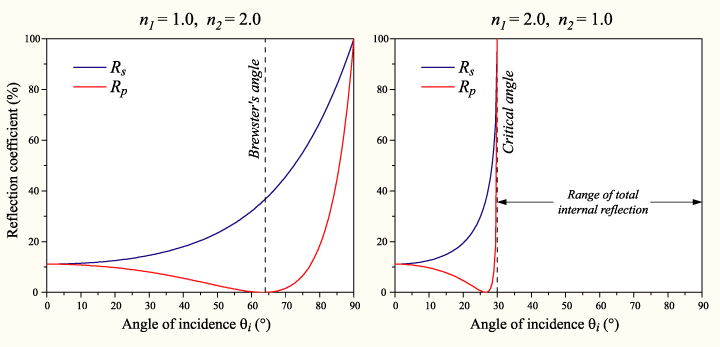
Para unos n₁ y n₂ dados, existe un ángulo característico para el cual, el valor de R_P se hace cero, y una onda incidente, polarizada en P, es totalmente refractada. Este ángulo es conocido como Angulo de Brewster. Para el vidrio y el aire (o vacío) el valor del Angulo de Brewster está alrededor de los 56º

En el caso en que se pasa de un medio de mayor densidad a otro menor (n₁ > n₂), según se va aumentando el ángulo de incidencia, se llega a un punto en que toda la luz es reflejada. En ángulo de incidencia que forma el rayo, en esta situación, se denomina Angulo Critico, y en este punto, R_S = R_P = 1. Este fenómeno es conocido como Reflexión Interna Total. Para el vidrio-aire, el Angulo Critico está en torno a los 41°.

Cuando el rayo incidente es aproximadamente normal a la superficie entre medios, (θ_i ≈ θ_t ≈ 0), los coeficientes de reflexión y transmisión esta dados por:

${\displaystyle R={{R}_{S}}={{R}_{P}}={{\left({\frac {{{n}_{1}}-{{n}_{2}}}{{{n}_{1}}+{{n}_{2}}}}\right)}^{2}}}$

${\displaystyle T={{T}_{S}}={{T}_{P}}={\frac {4{n}_{1}{n}_{2}}{{\left({{{n}_{1}}+{{n}_{2}}}\right)}^{2}}}}$

Para el vidrio común, el valor de la reflexión esta alrededor del 4%. No obstante, nótese que la reflexión en una ventana de vidrio, se da tanto en la cara externa como en la interna, y por lo tanto, parte de la luz transmitida vuelve a reflejarse un número indefinido de veces entre las dos caras del vidrio, y con intensidad decreciente. De esta forma, el coeficiente de reflexión combinado, es el límite de la suma infinita de estas reflexiones, y cuyo valor es:

${\displaystyle {\frac {2R}{1+R}}}$

Realmente, cuando la luz hace varias reflexiones entre dos superficies paralelas, los múltiples rayos de luz interfieren unos con otros, y de esta manera, la superficie actúa como un Interferómetro de Fabry-Perot”. Este efecto es el responsable de la coloración que se observa por ejemplo en las películas de aceite sobre el agua. Se aprovecha en óptica para la fabricación de coberturas que pueden disminuir la reflectividad, o que puedan ser usadas como filtro óptico.