dirección principal se refiere a una recta de puntos formada por vectores propios de alguna magnitud física de tipo tensorial. Los dos ejemplos más notorios son las direcciones principales de inercia, usualmente llamadas ejes principales de inercia y las direcciones principales de tensión y deformación de un sólido deformable.
Este artículo resume las propiedades matemáticas de las direcciones principales y el significado físico de las mismas en los diferentes contextos.
Definición matemática
Dada una magnitud física de tipo tensorial T se plantea el problema matemático de buscar los vectores no nulos v que cumplan la ecuación:
Dicho problema constituye un problema matemático de vectores propios, donde los autovalores (o valores principales) son valores del parámetro λ para los que existe solución y cada una de las rectas generadas por un vector v se llaman dirección principal. El significado físico tanto de los valores y direcciones principales varía según la magnitud tensorial considerada. En los siguientes apartados se explica el significado e importancia de valores y direcciones principales para algunas magnitudes tensoriales importantes.
Ejes principales de inercia
Como es sabido en mecánica del sólido rígido, la inercia rotacional de un cuerpo viene caracterizada por un tensor llamado tensor de inercia, que en una base ortogonal se expresa mediante una matriz simétrica.
Los ejes principales de inercia son precisamente las rectas o ejes formadas por vectores propios del tensor de inercia. Tienen la propiedad interesante de que un sólido que gira libremente alrededor de uno de estos ejes no varía su orientación en el espacio. En cambio, si el cuerpo gira alrededor de un eje arbitrario que no sea principal, el movimiento de acuerdo con las ecuaciones de Euler presentará cambios de orientación en forma de precesión y nutación.
El hecho de que el giro alrededor de un eje principal sea tan simple se debe a que, cuando un sólido gira alrededor de uno de sus ejes principales, el momento angular Ly la velocidad angular ω son vectores paralelos por estar ambos alineados con una dirección principal:
Donde λ es una magnitud escalar que coincide con el momento de inercia correspondiente a dicho eje. En general, un cuerpo rígido tiene tres momentos principales de inercia diferentes. Puede probarse además que si dos ejes principales se corresponden a momentos principales de inercia diferentes, dichos ejes son perpendiculares.
Todo cuerpo sólido tiene al menos un sistema de tres ejes de inercia principales (el tensor de inercia siempre se puede diagonalizar) aunque, en particular, el número sistemas de ejes de inercia principales puede llegar a ser infinito si el sólido rígido presenta simetría axial o esférica. En el caso de la simetría axial dos de los momentos de inercia relativos a sendos ejes tendrán el mismo valor y, en el caso de la simetría esférica, todos serán iguales. Los sólidos rígidos que tienen simetría esférica se denominan peonzas esféricas y, los que sólo tienen simetría axial, peonzas simétricas.
Direcciones principales de tensión y deformación
El estado de tensión-deformación de sólido deformable viene caracterizado por dos campos tensoriales asociados a la tensión y deformación del mismo (que a su vez están relacionados por la llamada ecuación constitutiva del material). Si examinamos un punto cualquiera del sólido y tomamos una base ortonormal, tenemos que el estado de tensión-deformación viene caracterizado por dos matrices simétricas asociadas al tensor tensión y al tensor deformación. Puesto que estas matrices son simétricas, al igual que sucede con el tensor de inercia admiten vectores propios.
Tensiones principales
Es decir, que existen vectores unitarios tales que la tensión en un plano perpendicular a los mismos en el punto de estudio cumplen que:
Donde σ es una magnitud escalar con unidades de tensión, llamada tensión principal. Dado un punto de un sólido deformable siempre existe al menos una tensión principal y como máximo tres valores diferentes. Y nuevamente dos direcciones principales de tensión asociadas a valores diferentes de la tensión principal son perpendiculares.
Físicamente las direcciones principales de tensión son perpendiculares a planos tales que en el punto considerado sólo existe una tensión normal al plano de valor σ pero no existen esfuerzos de cizalla ni tensiones tangenciales τ.
Deformaciones principales
Una deformación físicamente admisible de un sólido deformable viene caracterizada por un difeomorfismo TD cuyo jacobiano DTD(x,y,z) es positivo en todo instante y para todos los puntos del cuerpo. A partir de esta deformación admisible podemos construir el campo vectorial de desplazamientos y a partir de sus derivadas primeras construimos el llamado tensor deformación. Puede demostrarse que fijado un punto de un sólido deformable, toda deformación físicamente admisible puede aproximarse localmente por tres alargamientos (o acortamientos) εi según direcciones perpendiculares, el valor de estos alargamientos εi puede determinarse resolviendo para cada punto la siguiente ecuación:
Las tres direcciones según las cuales se producirían estos alargamientos son precisamente las rectas que pasan por el punto considerado y son paralelas a cada uno de los vectores ni. Si para una determinada dirección principal εi > 0 entonces en esa dirección tenemos alargamiento, mientras que εi < 0 corresponde a direcciones principales donde existe acortamiento.
equilibrado de ejes al proceso que se realiza para eliminar o corregir fuerzas o momentos de inercia indeseados en mecanismos que giran.
Introducción
A veces, es necesario eliminar o corregir fuerzas o momentos de inercia indeseados, y a esta técnica se le llama equilibrado de máquinas. Sabemos que en un ciclo de operación, el eslabón de referencia o soporte de la máquina soporta distintos esfuerzos, capaces de provocar vibraciones que pueden llegar a tener amplitudes peligrosas y por consecuencia llegar a aflojar tornillos, tuercas y remaches. Estas vibraciones, pese a no ser siempre peligrosas, si se aplican repetidamente sobre los cojinetes, provocan cargas que pueden causar la rotura de los mismos, es decir, el fallo de la máquina por fatiga. Además, producen ruidos muy molestos en el entorno de trabajo. Luego a la hora de diseñar una máquina será necesario reducir esas fuerzas de inercia causantes de las vibraciones.
Cuando un eslabón o un elemento de un mecanismo se encuentra en rotación pura, siempre va a poder estar completamente equilibrado, de tal forma que las fuerzas o momentos de inercia que provocan las vibraciones desaparezcan. En la práctica, si se va a diseñar, se suelen equilibrar todos los elementos que se encuentren en rotación, excepto cuando se desee que haya vibraciones concretas. Hay dos tipos de equilibrado en un elemento que gira:
- Estático
- Dinámico
El estático es una modificación o variante del dinámico, pero para que un elemento esté totalmente equilibrado se necesita que haya un equilibrado dinámico. Aun así, en ocasiones, el dinámico puede sustituirse por el estático, que es más fácil de resolver. Un elemento que gira se diseña de forma que el equilibrado esté incluido en su geometría. Pese a esto, las pequeñas variaciones en cada pieza producidas a la hora de la fabricación, y debido a las tolerancias aceptadas, siempre puede haber algún pequeño desequilibrio en estas. Esto deberá tenerse en cuenta y después de la fabricación, se deberá aplicar alguna técnica de equilibrado . Esto se hace de forma sencilla quitando o añadiendo material en los puntos calculados (ya que se puede determinar con precisión la magnitud y ubicación de los desequilibrios).
En este documento trataremos de explicar cómo se determina y se diseña el equilibrio estático y dinámico en los elementos que van a rotar, en concreto, vamos a analizar el equilibrado de los ejes.
Equilibrado estático
Para ver si un disco está en equilibrio estático, se pueden hacer unos sencillos experimentos: Se suponen un disco y un eje, apoyado este último en unos rieles rígidos, de manera que el eje pueda rodar sin ningún tipo de rozamiento. Se establece un sistema de referencia fijo en el disco que gire solidario con él. Pasos del experimento:
- Se empuja el disco con la mano y se deja rodar libremente el sistema disco-eje, hasta que se pare y entonces se marca con un lápiz el punto más bajo de la pieza.
- Repetir esto 4 o 5 veces.
- Ahora se analizan las marcas que hemos hecho:
- Si éstas están desperdigadas en distintos puntos por el contorno del disco y no coinciden, el disco estará equilibrado estáticamente.
- Si en cambio están todas en el mismo punto, es decir, si coinciden, podremos decir que el disco está estáticamente desequilibrado. Esto significa que el centro de masas del disco y el eje no coinciden.
La posición de las marcas con respecto a los ejes x e y indica la localización angular del desequilibrio, pero no la magnitud. No es probable que las marcas queden unas a 180º de otras. El desequilibrio se puede corregir eliminando material en los puntos donde hemos hecho las marcas o si se prefiere añadiendo material a 180º de ellas. Como no se conoce la magnitud del desequilibrio las correcciones deberán hacerse tanteando. Si queremos precisar la corrección que hay que introducir, podemos añadir una masa de prueba m:
Al añadir esta masa de prueba m (conocida), el disco girará un ángulo φ y luego se detendrá otra vez. Ése ángulo será fácil de determinar.
Las dos masas (la de prueba y la del centro de masas del disco) provocarán una fuerza cada una (el peso de cada una de ellas) que a la vez harán que haya dos momentos. Para calcular el desequilibrio plantearemos el equilibrio de momentos como se puede ver en la figura.
(ecuación 1)
(ecuación 1.1)
(ecuación 2) donde es el Desequilibrio
Para equilibrar el sistema habrá que colocar una masa en el punto A', es decir, a 180º de la marca hecha.
La ecuación del movimiento
Al montar un sistema eje-disco desequilibrados sobre unos cojinetes A y B, si se hacen girar estos cojinetes, aparecerá una fuerza centrífuga . La fuerza centrífuga actuará sobre el eje y provocará unas reacciones giratorias en los cojinetes A y B, como puede verse en la figura. Para describir las observaciones se introcue la siguiente notación:
- mtot: masa total
- m: masa no equilibrada (del desequilibrio)
- k: es la rigidez del eje. Sus unidades son N/m y especifica cuál es la magnitud de la fuerza a aplicar en el punto o para flectar al eje una distancia de unidad
- c: coeficiente de amortiguamiento viscoso
- O: centro del eje en el disco
- G: centro de masas del disco.
Suponiendo un sistema de referencia XYZ y tomando cualquier coordenada del eje X en cualquier dirección normal al eje de rotación, aplicamos el equilibrio de fuerzas en el punto O:
(3)
(3.1)
Resolviendo esta ecuación diferencial conseguiremos el movimiento de vibración del punto o del eje:
(4)
con ángulo de fase que es el ángulo que hay entre la fuerza centrífuga y la amplitud X de la vibración del eje. Si en la ecuación de la amplitud de X, (término situado en el denominador) fuera cero, x sólo dependería de , que normalmente suele ser muy pequeño, luego x sería muy grande. Al valor de que hace que sea cero se le llama velocidad angular natural, velocidad crítica o frecuencia circular natural:
(5)
Para el valor de se ha estudiado que no se producen vibraciones, salvo un desplazamiento amortiguado que tiende a cero. Este valor es el del amortiguamiento crítico.
Se define la relación de amortiguamiento como el cociente entre el amortiguamiento real y el crítico
(ecuación 6)
Para casi todos los sistemas mecánicos, si no se ha introducido amortiguamiento intencionadamente, su valor estará dentro del siguiente intervalo:
Si llamamos X a la amplitud del coseno tendremos que:
(ecuación 7)
luego podremos expresar la ecuación del movimiento del punto o del eje de la siguiente manera:
(ecuación 8)
Dividiendo el numerador y el denominador de la amplitud X por k, sustituyendo también por (excentricidad) y teniendo en cuenta las ecuaciones 5 y 6 , llegaremos a la siguiente expresión:
que nos da la razón de amplitudes de la vibración de un sistema disco-eje que gira.
Sin considerar el amortiguamiento (es decir, ) las masas del desequilibrio y la masas total son la misma, y si además sustituimos por , conseguiremos:
donde X es la amplitud de cualquier razón de frecuencias .
Si representamos en una gráfica la amplitud frente a la razón de frecuencias, se pueden obtener deducciones interesantes, como las relaciones de amplitud y de fase. Al arrancar el sistema la amplitud de la vibración es muy pequeña y a la vez que aumenta la velocidad del eje, aumenta también la amplitud, haciéndose infinita en la velocidad crítica. Esto es lo que llamamos resonancia. Cuando el eje pasa por la velocidad crítica, la amplitud cambia a un valor negativo y disminuirá según siga aumentando la velocidad del eje. La amplitud del movimiento llegará a un valor límite de , en cuyo caso el disco girará en torno a su centro de gravedad (que coincidirá con la línea del eje). Luego podremos concluir después de haber visto todo esto que cuando un sistema que rota está estáticamente desequilibrado, producirá vibraciones y reacciones giratorias indeseadas en los cojinetes.
Máquinas de equilibrado estático
Una máquina de equilibrado estático sirve para ver, como su propio nombre indica, si una pieza está equilibrada estáticamente o no, y en caso de no estarlo, calcular la magnitud y la localización del desequilibrio, es decir, sirve para medir el desequilibrio. Estas máquinas sirven sólo para calcular desequilibrios de piezas cuyas dimensiones axiales sean muy pequeñas, como por ejemplo: engranes, levas, poleas, ruedas, ventiladores, volantes, impulsores... A veces, se puede considerar que la masa de las piezas está concentrada en un solo plano, luego a estas máquinas se les suele llamar máquinas de equilibrado en un solo plano.
A la hora de montar más de una rueda sobre un eje, primero habrá que equilibrar estáticamente cada rueda individualmente, y después de montarlas se podrá equilibrar todo el conjunto. En la práctica, el proceso de equilibrado estático de un disco es un proceso de pesado. Existen dos métodos de equilibrado, dependiendo del tipo de fuerza que se le aplica a la pieza. La fuerza podrá ser de gravedad o centrífuga.
En el ejemplo visto anteriormente del conjunto disco-eje, la fuerza que se utilizaba para encontrar el desequilibrio era la de la gravedad. Otra forma de hacerlo sería haciendo girar al disco a una velocidad determinada. Así, se medirían las reacciones en los cojinetes, utilizando así sus magnitudes para calcular la magnitud del desequilibrio. Se utiliza un estroboscopio para dar la localización de la corrección, ya que la pieza gira cuando se hacen las mediciones.
Al fabricar grandes cantidades de piezas, lo que hace falta es una forma rápida de medir el desequilibrio y que diga cuál es la corrección. Si se evita hacer girar a la pieza se ahorra tiempo, luego el método más utilizado en estos casos sería el de aplicar una fuerza de gravedad.
Se suele utilizar un péndulo apoyado en un pivote, sobre el que se pone la pieza. Se utilizan amortiguamientos para evitar el balanceo del péndulo. Éste se inclinará un ángulo y bajará lógicamente por la dirección radial en la que se encuentre el desequilibrio, como podemos ver en la figura. Luego la dirección de la inclinación nos dará la ubicación del desequilibrio y el ángulo la magnitud.
Para hacer correctamente las mediciones des desequilibrio, se monta sobre la plataforma de la máquina de desequilibrio un nivel universal como el de la figura.
Una burbuja colocada en el centro, se mueve a la vez que el desequilibrio y mostrará la ubicación y la magnitud de la corrección del mismo.
Desequilibrio dinámico
Debemos tener en cuenta que, aunque un rotor esté equilibrado estáticamente, puede tener un desequilibrio dinámico. El desequilibrio dinámico se produce sólo cuando el rotor está girando.
En la figura vemos un rotor donde suponemos que se colocan 2 masas iguales en los extremos opuestos. Las masas ejercen una fuerza de forma que el rotor se mantiene equilibrado estáticamente.
Pero, cuando el rotor está girando, las fuerzas de inercia debidas a las masas dan lugar a un par de fuerzas que provoca un desequilibrio dinámico. Por tanto, podemos concluir que el equilibrado estático no es suficiente para equilibrar un rotor y por ello deberemos realizar un equilibrado dinámico, es decir en dos planos.
Análisis gráfico del desequilibrio
Para determinar tanto la magnitud como la distancia a la que debemos las correcciones en un eje giratorio desequilibrado dinámicamente utilizaremos las ecuaciones vectoriales para sistemas mecánicos en equilibrio:
(ecuación 1)
(ecuación 2)
Las fuerzas que aparecerán en la primera ecuación serán fuerzas de inercia (fuerzas centrífugas), que actuarán en dirección radial (del centro de rotación hacia cada una de las masas). Estas fuerzas son proporcionales a la masa, a la excentricidad de cada una de estas masas (R) y a la velocidad angular al cuadrado (ω²):
Fcen,i = mi Ri ω²
Los momentos que aparecerán en la segunda ecuación son los generados por las fuerzas de inercia.
Al ser la velocidad angular igual para todas las fuerzas de inercia, escalaremos los polígonos de fuerzas y momentos con el factor 1/ω² para facilitar cálculos ( no aparecerá el término de velocidad angular).
Los pasos a seguir para el ejemplo de la figura son:
1.- Hacer sumatorio de momentos (ecuación 2) de las fuerzas centrífugas respecto al punto A o al punto B (puntos de intersección de los planos de equilibrado con el eje) para evitar que aparezcan las fuerzas en el cojinete A y en el cojinete B respectivamente. En este caso está hecho respecto al punto A.
2.- Con ello construimos el polígono de momentos (figura c). Los vectores que constituyen este polígono tienen la dirección de los vectores de posición Ri de la figura a. Estos vectores deberían multiplicarse por w² y girarse 90º para que realmente fueran los momentos de las fuerzas de inercia. El vector de cierre del polígono (en azul) nos proporciona directamente el valor que equilibra el sistema dinámicamente. Así, una vez conocido el desequilibrio, podremos compensar el sistema eligiendo una de las dos magnitudes y obteniendo la otra del valor del desequilibrio calculado.
3.-Dado el equilibrio entre las fuerzas existentes (ecuación 1), construimos el polígono de fuerzas (figura d) y despejamos la corrección que debemos aplicar en el segundo plano (plano de corrección D).
Equilibrado dinámico
El desequilibrio se ha medido, por costumbre, en onza-pulgada, gramo-centímetro o gramo-pulgada. Pero, si usamos el sistema internacional, la unidad más apropiada es el miligramo-metro. El equilibrado es el hecho de determinar y corregir el desequilibrio. Como hemos visto anteriormente, cuando la masa se encuentra en un solo plano de rotación, ruedas, discos, etc.; basta con el equilibrado estático. Sin embargo, en rotores las fuerzas centrífugas que aparecen por el desequilibrio dan lugar a un par de fuerzas. El objetivo del equilibrado es medir ese par y realizar otro de las misma magnitud pero sentido contrario. Esto se puede hacer añadiendo o eliminando masas en dos planos cualesquiera llamados planos de corrección. Generalmente, los rotores suelen estar desequilibrados tanto estática como dinámicamente. Por tanto, para equilibrarlos necesitaremos conocer tanto la cantidad de masa como su ubicación en cada uno de los planos de corrección. Para medir estas dos magnitudes y corregir el desequilibrio pueden utilizarse tres métodos de uso general: bastidor basculante, punto nodal y compensación mecánica.
Bastidor basculante
En la figura podemos ver un rotor a equilibrar montado sobre unos rodillos de soporte que están sujetos a un bastidor basculante. Elegimos los planos de corrección que se harán coincidir con los pivotes. Nunca estarán los dos pivotes trabajando. Primero se libera un pivote y se hace girar el rotor. Se miden la magnitud y el ángulo de ubicación de la corrección. Luego se hace lo mismo pero liberando el otro pivote, ya que a las medidas no afectan los momentos en el plano del pivote fijo. Por tanto, los equilibrios medidos con el pivote derecho fijo serán corregidos en el plano de corrección de la izquierda y viceversa.
Punto nodal
Este método consiste en encontrar el punto de vibración cero. Para ello colocamos el rotor a equilibrar sobre cojinetes a un soporte conocido como barra nodal. Suponemos que el eje está equilibrado en el plano de corrección de la izquierda pero existe un desequilibrio en el de la derecha. Si se hace girar el rotor se produce una vibración del conjunto y la barra nodal gira en torno a algún punto. Para saber cual es ese punto deslizamos un reloj comparador sobre la barra nodal y vemos cuando el movimiento es cero. Ese punto será el punto nodal o nulo. Debemos recordar que hemos supuesto al principio que no existía desequilibrio en el plano de corrección de la izquierda. Por tanto, si existiera la magnitud del desequilibrio la marcaría el reloj comparador situado en el punto nodal calculado anteriormente independientemente del desequilibrio que existiera en el plano de la derecha.
Compensación mecánica
Este método se usará para lograr que un eje al girar lo haga con suavidad, sin vibraciones debidas a los desequilibrios. Además, el rotor girará con suavidad para toda velocidad de giro. El rotor se puede impulsar con una correa, una articulación universal, o se puede autoimpulsar si es por ejemplo, un motor.
Para hallar la magnitud y la dirección de las fuerzas que crean el desequilibrio fijamos al rotor dos masas (m) que giren solidarias con éste. Estas masas podrán distanciarse un ángulo β/2 cada una con respecto al eje común.
Por medio de dos controles obtendremos la magnitud y el desfase angular del desequilibrio M:
- Control de magnitud:
Variando el ángulo β obtendremos la magnitud del desequilibrio. Obsérvese que si β=0º la fuerza que crean las masas compensadoras es máxima, mientras que si β=180º ambas se contrarrestan y la única fuerza que queda en el rotor es la del desequilibrio.
- Control de ubicación:
La posición angular de los pesos compensadores con respecto al desequilibrio, dada por α, nos permitirá hallar la dirección en la que actúa la descompensación, es decir, el desfase angular del desequilibrio.
Equilibrado "in situ" con calculadora programable
Aunque un rotor se equilibre en el taller donde se fabrique, el transporte o el propio uso genera nuevos desequilibrios, lo que hace necesario que se vuelva a equilibrar. El no equilibrarlo conllevaría efectos no deseados como el desgaste prematuro de los rodamientos, roturas y fracturas por fatiga, deformaciones de los ejes e incluso podría suponer un peligro para los operarios en caso de fallo completo de la máquina.
Para ello utilizaremos el equilibrado “in situ”, haciendo uso de una calculadora programable y del álgebra compleja (métodos desarrollados por Rathbone y Thearle). Esto consiste en equilibrar un solo plano cada vez, haciéndolo dos o tres veces para cada plano para evitar los efectos cruzados y las interferencias en los resultados.
Si utilizamos letras en negrita para representar números complejos: R = ( R , θ )
Tras localizar los desequilibrios en los dos planos de referencia ( MI = (MI , φI) y MD = (MD, φD) ) mediremos las amplitudes y los desfases de las perturbaciones que generan en los cojinetes A y B con un equipo comercial de equilibrado “in situ” que designaremos mediante la letra X=(X, q). Para ello se utiliza el método de las tres carreras (tres ensayos diferenciados):
Primer ensayo: se miden las perturbaciones XA=(XA, θA) y XB=(XB, θB) en los cojinetes A y B debidas a los desequilibrios originales MI = (MI , θA) y MD = (MD, θB).
Segundo ensayo: se introduce una masa de ensayo al plano de corrección izquierdo () y se miden los desequilibrios ().
Tercer ensayo: se quita la masa de ensayo anterior y se repite el segundo ensayo poniendo una masa de ensayo en el plano de corrección derecho (con obtendré ).
Si definimos unas nuevas magnitudes también complejas (A y B) que denominaremos rigideces complejas y que reflejen la contribución de las masas de ensayo a las fuerzas creadas en los cojinetes:
Haciendo lo mismo para la segunda masa de ensayo (tercera carrera), podemos despejar las cuatro rigideces complejas y sustituyendo en las siguientes ecuaciones obtendremos la magnitud y la posición de los desequilibrios (recordar que son variables complejas):


![{\mathbf {t}}={\mathbf {T}}({\mathbf {n}})=\sigma {\mathbf {n}},\qquad \left[\Rightarrow t_{i}=\sum _{{j=1}}^{m}T_{{ij}}n_{j}=\sigma n_{i}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b0ce839688e2f72ea8a0b2c2f1449127809952)



 (ecuación 1)
(ecuación 1) (ecuación 1.1)
(ecuación 1.1) (ecuación 2) donde
(ecuación 2) donde  es el Desequilibrio
es el Desequilibrio en el punto A', es decir, a 180º de la marca hecha.
en el punto A', es decir, a 180º de la marca hecha.
 . La fuerza centrífuga actuará sobre el eje y provocará unas reacciones giratorias en los cojinetes A y B, como puede verse en la figura. Para describir las observaciones se introcue la siguiente notación:
. La fuerza centrífuga actuará sobre el eje y provocará unas reacciones giratorias en los cojinetes A y B, como puede verse en la figura. Para describir las observaciones se introcue la siguiente notación:


 que es el ángulo que hay entre la fuerza centrífuga y la amplitud X de la vibración del eje. Si en la ecuación de la amplitud de X,
que es el ángulo que hay entre la fuerza centrífuga y la amplitud X de la vibración del eje. Si en la ecuación de la amplitud de X,  (término situado en el denominador) fuera cero, x sólo dependería de
(término situado en el denominador) fuera cero, x sólo dependería de  , que normalmente suele ser muy pequeño, luego x sería muy grande. Al valor de
, que normalmente suele ser muy pequeño, luego x sería muy grande. Al valor de  que hace que
que hace que 
 se ha estudiado que no se producen vibraciones, salvo un desplazamiento amortiguado que tiende a cero. Este valor es el del amortiguamiento crítico.
se ha estudiado que no se producen vibraciones, salvo un desplazamiento amortiguado que tiende a cero. Este valor es el del amortiguamiento crítico.
 (ecuación 6)
(ecuación 6) estará dentro del siguiente intervalo:
estará dentro del siguiente intervalo: 
 (ecuación 7)
(ecuación 7) (ecuación 8)
(ecuación 8) por
por  (excentricidad) y teniendo en cuenta las ecuaciones
(excentricidad) y teniendo en cuenta las ecuaciones 
 ) las masas del desequilibrio y la masas total son la misma, y si además sustituimos
) las masas del desequilibrio y la masas total son la misma, y si además sustituimos 
 .
. , en cuyo caso el disco girará en torno a su centro de gravedad (que coincidirá con la línea del eje). Luego podremos concluir después de haber visto todo esto que cuando un sistema que rota está estáticamente desequilibrado, producirá vibraciones y reacciones giratorias indeseadas en los cojinetes.
, en cuyo caso el disco girará en torno a su centro de gravedad (que coincidirá con la línea del eje). Luego podremos concluir después de haber visto todo esto que cuando un sistema que rota está estáticamente desequilibrado, producirá vibraciones y reacciones giratorias indeseadas en los cojinetes.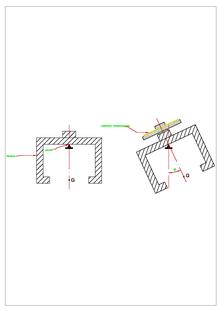




 (ecuación 1)
(ecuación 1) (ecuación 2)
(ecuación 2)



 ) y se miden los desequilibrios (
) y se miden los desequilibrios ( ).
). obtendré
obtendré  ).
).



No hay comentarios:
Publicar un comentario