Conceptos de electrónica

Los filtros pasivos

En los sistemas de comunicaciones se emplean filtros para dejar pasar solo las frecuencias que contengan la información deseada y eliminar las restantes.

Los filtros son usados para dejar pasar solamente las frecuencias que pudieran resultar ser de alguna utilidad y eliminar cualquier tipo de interferencia o ruido ajeno a ellas.

Existen dos tipos de filtros:

Filtros Pasivos: son aquellos tipos de filtros formados por combinaciones serie o paralelo de elementos R, L o C.

Los filtros activos son aquellos que emplean dispositivos activos, por ejemplo los transistores o los amplificadores operacionales, junto con elementos R L C.

En general se tienen los filtros de los siguientes tipos:

Pasa altas

Pasa bajas

Pasa bandas

Para cada uno de estos filtros existen dos zonas principales las cuales son llamadas Banda de paso y la banda de atenuación.

En la banda de paso, es donde las frecuencias pasan con un máximo de su valor, o hasta un valor de 70.71% con respecto a su original (la cual es la atenuación de –30 dB)

Filtro pasa bajas:

Es el primer filtro que se tiene, su funcionamiento es a base de un condensador y resistencia, este filtro tiene la siguiente configuración:

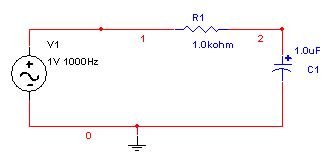
Su funcionamiento es el siguiente:

El condensador se comporta como una resistencia dependiente de la frecuencia por la relación de :

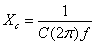
Es decir, para frecuencias muy bajas el condensador (por la regla de división de voltaje) al ser una resistencia muy alta, consume todo el voltaje, si s e conecta la salida en paralelo al condensador se tendrá el máximo de voltaje a la salida.

Conforme aumentemos la frecuencia de la fuente el condensador disminuye su impedancia, con lo que el voltaje que disipa disminuye , hasta tender a cero.

Este tipo de filtro tiene una gráfica de respuesta en frecuencia:

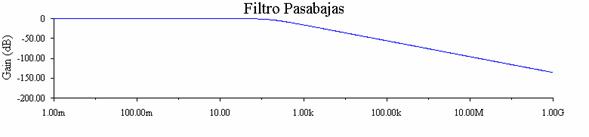
En cualquier frecuencia se puede determinar la salida de por medio de la regla divisora de voltaje:

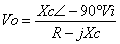
O para expresarlo en magnitud y en fase:

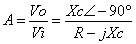
Separando en magnitud y fase

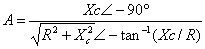
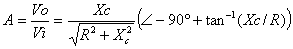
Entonces la magnitud queda expresada como:

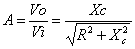
A un ángulo de fase :

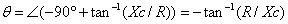
La frecuencia de corte se define como el punto de Vo=.7071Vi

Sustituyendo obtenemos que:

Filtro Pasa-altas

Este es el segundo de los filtros pasivo, el único cambio que presenta es la conexión de la salida, la cual en vez de tomarse del condensador se toma de la resistencia lo cual nos provoca que en vez de dejar “pasar” las frecuencia bajas pasen las frecuencias altas.

Circuito:

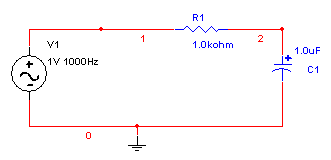
Como ya se menciono el circuito físicamente es igual que el anterior, solamente la salida se toma de la resistencia.

Explicación, cuando la frecuencia es demasiado baja, el voltaje se consume casi en su totalidad en el condensador, el cual se comporta como una impedancia de valor muy alto, por lo que en la salida no se tiene casi voltaje, cuando la frecuencia aplicada es aumentada se tiene que el valor de la impedancia representada por el condensador disminuyehasta que casi no consume voltaje, y la mayoría del voltaje se tiene a la salida.

Gráfica de salida:

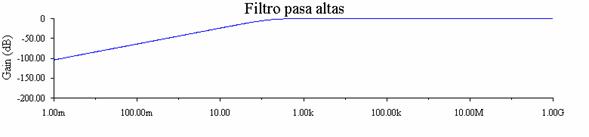
Estos dos filtros tienen un valor llamado frecuencia de corte, la cual es el valor de la frecuencia a partir del cual se considera que ya esta filtrando las señales.

Esta frecuencia esta determinada como la frecuencia en la que el valor de la salida con respecto a la entrada tiene una atenuación de -3dB. (o la salida es .717 del valor de la entrada).

Dependiendo de los valores elegidos de resistencia y capacitancia sera el valor de la frecuencia de corte.

Pero, para una resistencia fija, el valor de la frecuencia de corte depende del valor de el condensador

Siguiendo un procedimiento similar al anterior obtenemos que para el filtro pasa altas:

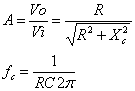
Filtro pasa bandas:

Este es un filtro que se compone de un filtro pasa bajas y uno pasa altas conectados en cascada.

Los componentes se deben de seleccionar para que la frecuencia de corte del filtro pasaaltas sea menor que la del filtro pasabajas.

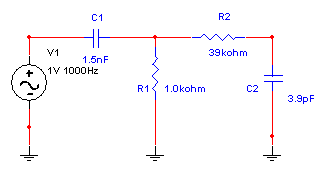
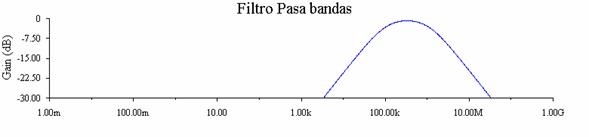
Las frecuencias de corte se pueden calcular con las formulas anteriores.

La característica mas importante de este circuito es el ancho de banda que permitiremos pasar, el ancho de banda es igual a la resta de las frecuencias de corte.

https://www.electronicafacil.net/tutoriales/Filtros-pasivos.php

web de filtro pasivos muy completa .- ...............:https://sites.google.com/a/goumh.umh.es/circuitos-electronicos-analogicos/practicas/practica-1

TIPOS DE FILTROS PASIVOS

La frecuencia de corte es el punto donde la respuesta en frecuencia se reduce a una fracción determinada. Este punto suele ser el punto de -3dB, que en potencia es el punto donde la respuesta se reduce a la mitad. Por la forma de percibir del oído humano, la disminución de la respuesta a la mitad no se percibe como "la mitad de alto" sino como "un poquito más bajo".

Un filtro puede dejar pasar las frecuencias mayores que la fecuencia de corte, o al contrario, dejar pasar sólo las frecuencias menores que la frecuencia de corte. O se pueden dejar pasar sólo las frecuencias de una banda (entre dos frecuencias de corte).

• Filtros paso alto: dejan pasar las frecuencia más altas que la fecuencia de corte.
• Filtros paso bajo: Dejan pasar las frecuencias menores que la fecuencia de corte.
• Filtros paso banda: Dejan pasar las frecuencias entre dos frecuencias de corte. Normalmente son una combinación en serie de un paso alto y un paso bajo, pero pueden implementarse de otras maneras.
• Filtro elimina banda: Al contrario que los paso banda, estos eliminan una banda. En altavoces no tiene mucho sentido. Al igual que los paso banda, pueden implementarse con un paso bajo y un paso alto, pero en paralelo.
• Otros: muesca (notch), y otras redes: Red Zobel, L-pad, ...

Los filtros pasivos se basan en la impedancia variable y dependiente de la frecuencia que tienen las bobinas y los condensadores.

Condensadores Cuanto mayor sea f, menor será su impedancia, por lo que un condensador dejará pasar las frecuencias altas y ofecerá una gran resistencia a las bajas frecuencias, que se verán atenuadas

Bobinas Cuanto mayor sea f, mayor será la impedancia de la bobina, por lo que a través de una bobina, pasarán sin ningún problema las frecuencias bajas, y las frecuencias altas se verán atenuadas, por atravesar una resistencia mayor. PARÁMETRO Q DE UN FILTRO A partir de ahora nos encontramos con un nuevo problema: La Q del filtro. Q suele ser sinónimo de un factor de calidad, pero en los filtros no tiene nada que ver con eso. Q define la proporción entre Z nominal, L y C. En los ejemplos de fórmulas y gráficas se han utilizado exclusivamente filtros de 2º oden, pero esto es común a todos los filtros de orden mayor a 1. El filtro de primer orden sólo tiene una Q, la de Butterworth. Dependiendo de los valores de Q se obtiene respuesta u otra en la banda cercana a la frecuencia de corte. Algunos de estos valores de Q producen que una característica sea óptima: respuesta plana, alineamiento en fase o brusquedad de la caída. Ahora ya no tiene mucho sentido hablar de 6, 12, 18 o 56dB/oct, porque eso son comportamientos asintóticos, muy por debajo de la banda audible, o por lo menos sin enmascarar. Sin embargo, nos referiremos al orden para indicar ese comportamiento. Los tipos de filtro más importantes en función de Q, para altavoces y audio son los siguientes: Butterworth: Produce la respuesta en frecuencia más plana posible. Tchebychev: Produce la caída más brusca de todas, a pesar de tener un pico de respuesta cerca de la frecuencia de corte. Este es el motivo por el que no se use demasiado. Bessel: No decae tan rápido como los anteriores, pero produce los menores errores de fase de todos. Linkwitz-Riley: El punto de corte no se produce a -3dB, sino a -6dB. Se construye a partir de dos filtros butterworth de orden menor. Como ventajas tiene que la respuesta es plana y sobre todo:en todo momento la reproducción de ambos drivers está en fase. Es una idea diferente a los filtros convencionales y es exclusiva del audio. En lugar de definir Q con un número, que cambia para diferentes órdenes, se emplean los nombres de matemáticos ilustres que definieron funciones que luego han sido usadas para deducir el comportamiento de los filtros en base al comportamiento de esas funciones (sobreamortiguado, subamortiguado...). Entre ellos están Bessel, Tchebychev, Butterworth, Legendre, Cauer,... En el caso del Linkwitz-Riley, Siegfrid Linkwitz es un prestigioso ingeniero que ahora retirado se dedica a la acústica. Las peculiaridades de su configuración son que la suma eléctrica del paso bajo y paso alto es exactamente 1, y ambos filtros reproducen con la misma fase. La respuesta es completamente plana y la readición sonora muy homogénea. En la gráfica de la derecha se ve cómo se comportan estos filtros dependiendo de su Q. Por debajo de la parte mostrada en la gráfica, el filtro de Tchebychev es el que más atenuación produce. El de Bessel, el que menos. Puede parecer en un principio que el de Tchebychev no sirve para nada, tiene un gran pico en la respuesta,... Esto es porque se muestra la respuesta en voltaje. Falta la intensidad, y juntas la intensidad y el voltaje forman la potencia. En potencia, que es como funciona un filtro pasivo, no hay ganancia de ningún tipo. Algo pasivo no puede producir ganancia. Parámetro Q de un filtro ver circuito Pero en circuitos activos más complejos, la propiedad de atenuar más que los demás hace que un filtro de 6º orden Tchebychev acabe funcionando mejor que uno de Butterworth de 8º orden. De hecho, es la Q que se utiliza en los filtros anti-alising en los conversores analógico-digital. A la izquierda se ve cómo se comporta la fase de cada filtro. La peor es la de Tchebychev, es la que mas cambios bruscos produce, y el de Bessel es el más suave. Butterworth, como en el caso anterior, es algo intermedio. En el fondo es un compromiso entre fase, respuesta temporal, respuesta en frecuencia y atenuación en la banda eliminada. No se puede tener todo a la vez, así que hay que decidir cual es el factor más importante. inicio SUMA DE LAS RESPUESTAS Una vez que la señal pasa por el filtro, llega al altavoz. Pero quedan cosas pendientes. Queda por saber qué pasa cuando el sonido sale del altavoz. Hay que pensar que está desplazado en fase. Vamos a ver qué nuevos problemas surgen ahora en el caso concreto del filtro de 2º orden. Ahora, a la derecha tenemos las señales que resultan de filtar, paso bajo y paso alto, para conectarlas a los drivers. Se ha señalado la Q de todos los filtros Y la suma de las respuestas tiene este aspecto, desolador. ¿qué es lo que está pasando? Pues que a la frecuencia de corte el desfase es de 180º, y eso supone que una se resta a la otra, y esuna cancelación perfecta. La solución es invertir la fase de uno de los dos altavoces (cambiar el cable rojo por el negro, así de fácil). Normalmente se invierte la fase del de agudos, ya que en los agudos no es posible percibir la fase absoluta. La suma en voltaje más plana es la de Linkwitz-Riley, granate. La siguiente es la de Butterworth, azul oscuro. A la derecha se vé la fase de la suma de ambas pastes del filtro en el caso que están los dos altavoces en fase. Se vé que el desfase máximo es de 90º. El caso en el que más bruscamente se desvía la fase es el de Tchebichev y el que menos, el de Bessel. Ahora, la respuesta en fase de la suma con el tweeter invertido de fase. Se aleja de cero, pero esto es a costa de no tener una cancelación. Es el precio que hay que pagar. Esto es común a los filtros de orden par. Hay que elegir entre una cancelación o un desfase, y es completamente lógico elegir el desfase, es decir, hay que invertir la polaridad del tweeter. Esto es así con los de 2, 4º, 6º,...orden, excepto en el filtro activo de 4º orden LR, donde no hay que invertir la fase de ninguno de los drivers. En el caso de un filtro de orden impar, concretamente el 3er orden tenemos este resultado. Se trata de un filtro de 3er orden Butterworth. Se puede observar a primera vista que la suma de las respuestas es perfectamente plana. En caso de invertir la fase del tweeter también es plana. La respuesta en fase se muestra a la derecha. Los drivers reproducen a +135º y -135º a 1kHz, la frecuencia de corte. Esto quiere decir que hay un desfase de 270º entre ellos... o visto de otra manera, -90º. Es un artificio matemático perfectamente válido. a pesar de lo aparatosa que resulta la gráfica, la respuesta en fase no está mal para ser un filtro de 3er orden. La tentación de invertir la fase del tweeter puede ser demasiado grande. A la derecha se ve lo que pasa en ese caso. La respuesta tiene un desfase de -90º a la frecuencia de corte, pero luego avanza hacia los 180º que tiene el tweeter de desfase. En definitiva, no produce ningún beneficio sin que produzca otro perjuicio. Como viene siendo habitual, es cuestión de decidir qué característica nos conviene. inicio GROUP DELAY (retardo de grupo) El retardo de grupo es la variación del desfase (fi) frente a la frecuencia angular (omega), que es proporcional a la frecuencia. Es una magnitud que ha permanecido ignorada durante mucho tiempo pero parece que ahora empieza por fin a despertar interés. Es una medida de la respuesta temporal que produce un filtro. Cuanto más grande, más tiempo tarda en reaccionar, pero no es un problema de tiempo sino de uniformidad. No podemos percibir un retraso absoluto en la música, es como pulsar el play 300 microsegundos antes o después, pero se puede distinguir cuándo el platillo empieza a sonar en relación con el bombo. Los casos más dramáticos se producen en graves, donde los desfases y los retrasos temporales son perceptibles por nuestro oído. En los casos de las cajas acústicas basadas en sistemas resonantes, como las bass-reflex y las paso banda, es donde mayor importancia tiene, cuando los retrasos empiezan a superar los 25ms, cosa que nuestro oído percibe como un eco. A la derecha se observa el retardo de grupo para los 4 órdenes de filtro visto aquí. Todos son de Q Butterworth. Es obvio que no sólo aumenta el retraso, sino que aumenta también su no uniformidad, que es el principio del problema. Group delay frente al orden Aquí se muestra la dependencia del retardo de grupo con la Q del filtro. Tras ver las dos gráficas ya se puede deducir algo. Cuanto mayor es la atenuación del filtro, mayor es la no uniformidad y peor la respuesta temporal. La Q de Bessel es la mejor mientras que la de Chebychev es la peor. Group delay frente a Q El resultado de todo lo expuesto anteriormente (fase, respuesta tempora, group delay,... es el "ringing", o sobreoscilación. Es una distosión añadida por el filtro a la onda original. El ejemplo más acertado es la onda cuadrada, que aunque muchos opinan que no es un test válido, resulta ser la onda con mayor contenido en armónicos y la más exigente para la respuesta temporal. A la derecha se observa una onda cuadrada con un periodo de 10ms. Respuesta a la onda cuadrada En el detalle de la derecha se aprecia mejor: el filtro de Tchebychev produce unos picos bastante grandes. Le sigue el de Butterworth, algo mejor. Luego vienen Bessel y L-R con una respuesta bastante buena.. Detalle de la sobreoscilación El circuito empleado para esta última simulación se muestra aqui. Son los filtros de 2º orden con una entrada de onda cuadrada.