Términos de Geografía

Ecuador magnético se refiere a una línea curva que discurre en las proximidades del ecuador geográfico, uniendo los punto 0 de inclinación magnética, el punto donde más se aleja el ecuador magnético del ecuador terrestre geodésico es en el 15°S en Sudamérica (quizás en relación con la Anomalía del Atlántico Sur).

El ecuador magnético es el grado cero o punto de partida para definir una latitud magnética.

La ecúmene (del griego οἰκουμένη, oikouménē, «[tierra] habitada»)¹ es el conjunto del mundo conocido por una cultura. Generalmente se distingue como aquella porción de la Tierra permanentemente habitada, en contraposición al anecúmene o áreas deshabitadas o temporalmente ocupadas.

Historia del término

Durante el período helenístico, ecúmene hacía referencia a la parte de la Tierra que estaba habitada, ya fuera por toda la humanidad o sólo por un subconjunto de ésta. Con frecuencia se refería a las tierras habitadas por los griegos, excluyendo aquellas que estaban ocupadas por los bárbaros.

En la koiné del Imperio romano y el Nuevo Testamento, ecúmene significa literalmente mundo; sin embargo, por lo general se entendía que hacía referencia al mundo romano.

Los bizantinos utilizaban ecúmene para referirse al Imperio bizantino (véase también concilio ecuménico). El concepto subyace al título de Patriarca ecuménico que se le da al Patriarca de Constantinopla, así como al proceso del ecumenismo.

La ecúmene en el cristianismo

En el Nuevo Testamento el término puede hacer referencia al futuro reino de Cristo:

5 Οὐ γὰρ ἀγγέλοις ὑπέταξεν τὴν οἰκουμένην τὴν μέλλουσαν, περὶ ἧς λαλοῦμεν·

5 Porque no sujetó a los ángeles el mundo venidero, acerca del cual estamos hablando;

Hebreos 2:5.²

Ecúmene en la ficción

• J. R. R. Tolkien describió su Tierra Media como el equivalente de lo que los griegos llamaban ecúmene: el lugar en que vivían los hombres.
• En la serie de novelas de ciencia ficción Los príncipes demonio, escrita por Jack Vance, el término Oikumene se refiere a los mundos de la galaxia habitados por seres humanos.
• En La mano izquierda de la oscuridad y otras obras relacionadas de Ursula K. LeGuin, el Ekumen es una suerte de confederación de mundos habitados, unidos por comunicación instantánea, pero separados por el viaje más lento que la luz.
• En la trilogía La edad de oro de John C. Wright, la Ecúmene Dorada es una unidad política que abarca parte del sistema solar.
• En el universo de Halo, la ecúmene es la forma de afiliación política de los Forerunner.

Reconstrucción del mapa de la Ecúmene de Heródoto, circa 450 a. C.

El efecto Coriolis, descrito en 1836 por el científico francés Gaspard-Gustave Coriolis, es el efecto que se observa en un sistema de referencia en rotación cuando un cuerpo se encuentra en movimiento respecto de dicho sistema de referencia. Este efecto consiste en la existencia de una aceleración relativa del cuerpo en dicho sistema en rotación. Esta aceleración es siempre perpendicular al eje de rotación del sistema y a la velocidad del cuerpo.

El efecto Coriolis hace que un objeto que se mueve sobre el radio de un disco en rotación tienda a acelerarse con respecto a ese disco según si el movimiento es hacia el eje de giro o alejándose de éste. Por el mismo principio, en el caso de una esfera en rotación, el movimiento de un objeto sobre los meridianos también presenta este efecto, ya que dicho movimiento reduce o incrementa la distancia respecto al eje de giro de la esfera.

Debido a que el objeto sufre una aceleración desde el punto de vista del observador en rotación, es como si para éste existiera una fuerza sobre el objeto que lo acelera. A esta fuerza se le llama fuerza de Coriolis, y no es una fuerza real en el sentido de que no hay nada que la produzca. Se trata pues de una fuerza inercial o ficticia, que se introduce para explicar, desde el punto de vista del sistema en rotación, la aceleración del cuerpo, cuyo origen está en realidad, en el hecho de que el sistema de observación está rotando.

Un ejemplo canónico de efecto Coriolis es el experimento imaginario en el que disparamos un proyectil desde el Ecuador en dirección norte. El cañón está girando con la tierra hacia el este y, por tanto, imprime al proyectil esa velocidad (además de la velocidad hacia adelante al momento de la impulsión). Al viajar el proyectil hacia el norte, sobrevuela puntos de la tierra cuya velocidad lineal hacia el este va disminuyendo con la latitud creciente. La inercia del proyectil hacia el este hace que su velocidad angular aumente y que, por tanto, adelante a los puntos que sobrevuela. Si el vuelo es suficientemente largo (ver cálculos al final del artículo), el proyectil caerá en un meridiano situado al este de aquél desde el cual se disparó, a pesar de que la dirección del disparo fue exactamente hacia el norte. Finalmente, el efecto Coriolis, al actuar sobre masas de aire (o agua) en latitudes intermedias, induce un giro al desviar hacia el este o hacia el oeste las partes de esa masa que ganen o pierdan latitud o altitud en su movimiento.

Una bolita se mueve sin fricción sobre un plato de sección parabólica que está girando a velocidad constante. La gravedad tira de la bolita hacia el centro con una fuerza directamente proporcional a la distancia respecto a éste. La fuerza centrífuga (o, mejor dicho, la ausencia de fuerza centrípeta) tira de la bolita hacia afuera. La conservación del momento angular cambia la velocidad angular de la bolita cuando ésta se mueve hacia dentro (acelera) y hacia afuera (frena). También puede expresarse diciendo que, para mantener su velocidad lineal, la bolita cambia su velocidad angular al variar la distancia respecto al eje. En cualquier caso, la magnitud subyacente es la inercia y la desviación que sufre la bolita con respecto a la dirección de los radios es el efecto Coriolis.
Izquierda: El movimiento observado desde un punto de vista externo.
Derecha: El movimiento visto desde un punto de vista solidario con el sistema no inercial.

Introducción

La tendencia de giro varía según el hemisferio considerado. La ilustración muestra el patrón para los anticiclones. Las borrascas giran en sentido opuesto.

La fuerza de Coriolis es una fuerza ficticia que aparece cuando un cuerpo está en movimiento con respecto a un sistema en rotación y se describe su movimiento en ese referencial. La fuerza de Coriolis es diferente de la fuerza centrífuga. La fuerza de Coriolis siempre es perpendicular a la dirección del eje de rotación del sistema y a la dirección del movimiento del cuerpo vista desde el sistema en rotación. La fuerza de Coriolis tiene dos componentes:

• una componente tangencial, debida a la componente radial del movimiento del cuerpo, y
• una componente radial, debida a la componente tangencial del movimiento del cuerpo.

La componente del movimiento del cuerpo paralela al eje de rotación no engendra fuerza de Coriolis. El valor de la fuerza de Coriolis ${\displaystyle \scriptstyle {\mathbf {F} _{c}}}$ es:

${\displaystyle {\vec {F}}_{c}=-2m\left({\vec {\omega }}\times {\vec {v}}\right),}$

donde:

${\displaystyle \scriptstyle {m}}$ es la masa del cuerpo.

${\displaystyle \scriptstyle {\mathbf {v} }}$ es la velocidad del cuerpo en el sistema en rotación .

${\displaystyle \scriptstyle {\mathbf {\omega } }}$ es la velocidad angular del sistema en rotación vista desde un sistema inercial.

${\displaystyle \scriptstyle {\times }}$ indica producto vectorial.

Historia

En 1835, Gaspard-Gustave de Coriolis, en su artículo Sur les équations du mouvement relatif des systèmes de corps,¹ describió matemáticamente la fuerza que terminó llevando su nombre. En ese artículo, la fuerza de Coriolis aparece como una componente suplementaria a la fuerza centrífuga experimentada por un cuerpo en movimiento relativo a un referencial en rotación, como puede producirse, por ejemplo, en los engranajes de una máquina. El razonamiento de Coriolis se basaba sobre un análisis del trabajo y de la energía potencial y cinética en los sistemas en rotación. Ahora, la demostración más utilizada para enseñar la fuerza de Coriolis utiliza las herramientas de la cinemática.

Esta fuerza no comenzó a aparecer en la literatura meteorológica y oceanográfica hasta finales del siglo XIX. El término fuerza de Coriolis apareció a principios del siglo XX.

Formulación y demostración

Para demostrar la expresión analítica expresada en la introducción, pueden usarse dos aproximaciones diferentes: por conservación del momento angular o por derivación en base móvil. A continuación se explican ambas.

Demostración por conservación del momento angular

En un sistema de coordenadas cilíndricas, la velocidad (en negro) de un punto puede descomponerse en una velocidad radial (en magenta), una velocidad axial (en azul) y una velocidad tangencial (en verde).

Es preciso recordar que cuando un observador en un sistema no inercial (como lo es un sistema en rotación) trata de comprender el comportamiento de su sistema como si fuese un sistema inercial ve aparecer fuerzas ficticias. En el caso de un sistema en rotación, el observador ve que todos los objetos que no están sujetos se alejan de manera radial como si actuase sobre ellos una fuerza proporcional a sus masas y a la distancia a una cierta recta (el eje de rotación). Esa es la fuerza centrífuga que hay que compensar con la fuerza centrípeta para sujetar los objetos. Por supuesto, para un observador externo, situado en un sistema inercial (sistema fijo), la única fuerza que existe es la fuerza centrípeta, cuando los objetos están sujetos. Si no lo están, los objetos tomarán la tangente y se alejarán del eje de rotación.

Si los objetos no están inmóviles con respecto al observador del sistema en rotación, otra fuerza ficticia aparece: la fuerza de Coriolis. Visto desde el sistema en rotación, el movimiento de un objeto se puede descomponer en una componente paralela al eje de rotación, otra componente radial (situada sobre una línea que pasa por el eje de rotación y perpendicular a éste), y una tercera componente tangencial (tangente a un círculo centrado en el eje y perpendicular a éste) (ver gráfica).

Un objeto que se desplaza paralelamente al eje de rotación, visto de un sistema fijo, gira con el sistema en rotación a la misma velocidad angular y con radio constante. La única fuerza que actúa sobre el objeto es la fuerza centrípeta. El observador del sistema en rotación sólo nota la fuerza centrífuga contra la cual hay que oponerse para que se quede a la misma distancia del eje.

Cuando se reduce el radio de rotación de un cuerpo sin aplicar un torque, el momento angular se conserva y la velocidad tangencial aumenta. En cambio, si se obliga al cuerpo a conservar la misma velocidad angular, la velocidad tangencial disminuye. El esquema está visto desde un sistema fijo (inercial).

Supóngase que un observador en el sistema en rotación mantiene una masa ${\displaystyle \scriptstyle {m}}$ a una distancia ${\displaystyle \scriptstyle {R}}$ del eje de rotación mediante un hilo de masa despreciable. El observador tira del hilo y modifica ligeramente el radio de rotación de la masa de ${\displaystyle \scriptstyle {\Delta R}}$. Eso le ha tomado un tiempo ${\displaystyle \scriptstyle {\Delta t}}$. Como el momento dinámico es nulo, el momento angular de la masa se conserva. Si ${\displaystyle \scriptstyle {V}}$ es la velocidad de la masa, la conservación del momento angular expresa:

${\displaystyle \Delta L=\Delta (mVR)=m(\Delta V\,R+V\Delta R)=0}$

${\displaystyle \Delta V_{1}=-V\textstyle {\Delta R \over R}}$

El signo menos indica que cuando el radio aumenta la velocidad tangencial disminuye.

Si la masa se moviese siguiendo una trayectoria radial, fija con respecto al sistema en rotación, conservando en consecuencia la misma velocidad angular ${\displaystyle \scriptstyle {\omega }}$ del sistema en rotación, su velocidad lineal habría aumentado de ${\displaystyle \scriptstyle {\Delta V_{2}=\omega \Delta R}}$ (o disminuido, si ${\displaystyle \scriptstyle {\Delta R}}$ es negativo). Para un observador fijo, entre la velocidad de la masa que se ve obligada a seguir una trayectoria radial y la velocidad de la masa que conserva su momento angular hay una diferencia de:

${\displaystyle \Delta V_{3}=\Delta V_{1}-\Delta V_{2}=-V\textstyle {\Delta R \over R}-\omega \Delta R=-\omega \Delta R-\omega \Delta R=-2\omega \Delta R}$

Como el objeto no está sujeto al sistema en rotación, el observador en ese sistema ve la masa tomar una velocidad lateral ${\displaystyle \scriptstyle {\Delta V_{3}}}$. Eso se interpreta como la aplicación de una fuerza lateral (de Coriolis). Si el cambio de velocidad tomó ${\displaystyle \scriptstyle {\Delta t}}$ segundos, la aceleración de Coriolis será (en valor absoluto):

${\displaystyle a_{c}=\textstyle {\Delta V_{3} \over \Delta t}=2\omega \textstyle {\Delta R \over \Delta t}=2\omega V_{r}}$,

donde ${\displaystyle \scriptstyle {V_{r}}}$ es la velocidad radial. Esa aceleración corresponde a una fuerza (de Coriolis) de:

${\displaystyle F_{c}=2m\omega V_{r}\,}$

Considerando un objeto con velocidad tangencial ${\displaystyle \scriptstyle {V_{t}}}$ vista por el observador en el sistema en rotación. Esta vez, la misma masa tenida por un hilo tiene una velocidad angular diferente del sistema en rotación. Para el observador en el sistema en rotación, las fuerzas que nota aplicadas a la masa para que siga una trayectoria circular son: la fuerza centrífuga ${\displaystyle \scriptstyle {m\omega ^{2}R}}$ que ve aplicada en todos los objetos, más la fuerza centrípeta debido a la rotación aparente de la masa ${\displaystyle \scriptstyle {m{V^{2} \over R}}}$. Pero eso no basta. Hay aún otra fuerza aparente, y es precisamente la fuerza de Coriolis. Se calcula ahora la fuerza centrípeta que ve un observador fijo: la velocidad tangencial es ${\displaystyle \scriptstyle {V_{\circ }=\omega R+V_{t}}}$. Para este observador, la fuerza centrípeta que mantiene la masa a distancia constante será:

${\displaystyle F_{\circ }=m\textstyle {V^{2} \over R}=m\textstyle {\left(\omega R+V_{t}\right)^{2} \over R}=m\textstyle {\left(\omega ^{2}R^{2}+2\omega RV_{t}+{V_{t}^{2}}\right) \over R}=m\left(\omega ^{2}R+2\omega V_{t}+\textstyle {V_{t}^{2} \over R}\right)}$

El primer término es la fuerza centrífuga común a todos los objetos que giran con el sistema en rotación. El tercero es la fuerza centrípeta debida a la rotación de la masa con respecto al sistema en rotación. Y el segundo término es la fuerza de Coriolis. Es un término suplementario debido al hecho de que la fuerza centrípeta depende del cuadrado de la velocidad tangencial y no puede obtenerse sumando las fuerzas centrífuga y centrípeta debido a velocidades parciales. La fuerza de Coriolis es:

${\displaystyle F_{c}=2m\omega V_{t}\,}$

Como se ha dicho , esa fuerza es radial.

Demostración por la derivación en base móvil

Para esta demostración se utilizará el subíndice abs para indicar magnitudes vistas desde el sistema de referencia inercial, es decir, uno donde el espacio sea homogéneo e isótropo y donde el tiempo sea constante. El subíndice rel (relativa) se refiere a magnitudes vistas desde una referencia no galileana o no inercial. El subíndice ar (arrastre) hace referencia al movimiento de la base móvil respecto a la base fija. También es necesario conocer cómo se deriva en una base móvil:

${\displaystyle {\dot {\mathbf {r} }}=\sum _{i=1}^{3}{{\dot {r}}_{i}\mathbf {e} _{i}}+\sum _{i=1}^{3}{r_{i}{\dot {\mathbf {e} }}_{i}}=\sum _{i=1}^{3}{{\dot {r}}_{i}\mathbf {e} _{i}}+\mathbf {r} \times {\boldsymbol {\Omega }}_{ar}}$

Una aceleración es un cambio en la magnitud o en la orientación de la velocidad respecto del tiempo. Para esa demostración se considera un movimiento que no varía la magnitud de su velocidad, es decir, que no está sometido a fuerzas que tengan alguna componente en la dirección del movimiento. Entonces:

${\displaystyle \mathbf {a} _{abs}(P)={\dot {\mathbf {v} }}_{abs}(P)={\dot {\mathbf {v} }}_{rel}(P)+{\dot {\mathbf {v} }}_{ar}(P)}$

Por una parte:

${\displaystyle {\dot {\mathbf {v} }}_{rel}=\mathbf {a} _{rel}(P)+{\boldsymbol {\Omega }}_{ar}\times \mathbf {v} _{rel}}$

Por otra:

${\displaystyle {\dot {\mathbf {v} }}_{ar}=\mathbf {a} _{abs}(O_{rel})+({\boldsymbol {\Omega }}_{ar}\times {\overline {O_{rel}P}})'+{\boldsymbol {\Omega }}_{ar}\times ({\boldsymbol {\Omega }}_{ar}\times {\overline {O_{rel}P}})}$

donde:

${\displaystyle (\Omega _{ar}\times {\overline {O_{rel}P}})'={\dot {\Omega }}_{ar}\times {\overline {O_{rel}P}}+\Omega _{ar}\times {\dot {\overline {O_{rel}P}}}}$

Como no se considera el movimiento alrededor del Sol, sino sólo el giro de la tierra en torno a sí misma:

${\displaystyle \mathbf {a} _{abs}(O_{rel})=0,\qquad {\dot {\boldsymbol {\Omega }}}_{ar}=0}$

Además, como se está imaginando un movimiento sin aceleración relativa (como el de un proyectil):

${\displaystyle \mathbf {a} _{rel}(P)=0\,\!}$

quedando así:

${\displaystyle {\dot {v}}_{rel}=0+\Omega _{ar}\times v_{rel}}$

${\displaystyle {\dot {v}}_{ar}=0+\Omega _{ar}\times {\dot {\overline {O_{rel}P}}}+\Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})}$

Pero:

${\displaystyle {\dot {\overline {O_{rel}P}}}=v_{rel}}$

Entonces:

${\displaystyle {\dot {v}}_{ar}=\Omega _{ar}\times {\dot {\overline {O_{rel}P}}}+\Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})=\Omega _{ar}\times v_{rel}+\Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})}$

Volviendo al principio:

${\displaystyle a_{abs}(P)={\dot {v}}_{abs}(P)={\dot {v}}_{rel}(P)+{\dot {v}}_{ar}(P)=\Omega _{ar}\times v_{rel}+\Omega _{ar}\times v_{rel}+\Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})=2\cdot \Omega _{ar}\times v_{rel}+\Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})}$

La aceleración de Coriolis es el primer sumando:

${\displaystyle 2\cdot \Omega _{ar}\times v_{rel}}$

La aceleración centrípeta es el segundo:

${\displaystyle \Omega _{ar}\times (\Omega _{ar}\times {\overline {O_{rel}P}})}$

Meteorología, oceanografía y fuerza de Coriolis

El ejemplo más notorio de manifestación del efecto Coriolis se da cuando masas de aire o de agua se desplazan siguiendo meridianos terrestres, y su trayectoria y velocidad se ven modificadas por él.² En efecto, los vientos o corrientes oceánicas que se desplazan siguiendo un meridiano se desvían acelerando en la dirección de giro (este) si van hacia los polos o al contrario (oeste) si van hacia el ecuador. Se puede añadir, que por consecuencia, en el Ecuador, no hay efecto de Coriolis. La manifestación de estas desviaciones produce, de manera análoga al giro de la bolita mostrado al principio, que las borrascas tiendan a girar en el hemisferio sur en el sentido de las agujas del reloj y, en el hemisferio norte, en sentido contrario.

El efecto de la fuerza de Coriolis deberá considerarse siempre que se estudie el movimiento de fluidos y también el de cualquier objeto móvil sobre esferas o superficies planas en rotación. Esto incluye a los planetas gaseosos del sistema solar, el Sol y todas las estrellas y, en el planeta Tierra, el movimiento de las aguas de los ríos, los lagos, los océanos y, por supuesto, de la atmósfera. El efecto de Coriolis predice que siempre que se observen los movimientos giratorios de esos cuerpos, los vórtices seguirán la norma descrita para las borrascas y anticiclones terrestres.³

Además de su influencia sobre la atmósfera, es muy notoria la que tiene también sobre la circulación oceánica. En las cuencas que tienen la forma apropiada (como, por ejemplo, la cuenca del Atlántico norte y la del Atlántico sur), el efecto Coriolis desvía a las corrientes marinas hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur, de la misma manera que sucede con la circulación general de los vientos.

Las excepciones o modificaciones de este patrón general de la circulación general de los océanos tienen que ver con la disposición de las costas y la compensación introducida por las corrientes cálidas que van, en los océanos, de las costas orientales de la zona intertropical hacia las occidentales de las zonas templadas de los continentes (corriente del Golfo y de Kuro Shivo, especialmente). Además, en los océanos, lo mismo que sucede en la atmósfera, se produce una especie de convergencia en las latitudes ecuatoriales por la fuerza centrífuga del movimiento de rotación: tanto el océano como la atmósfera tienen un abombamiento ecuatorial por la rotación terrestre, de varios kilómetros de altura en el caso de los océanos y aún mayor en el caso de la atmósfera debido a su menor densidad. A su vez, este "abombamiento" ocasiona una especie de obstáculo a la libre circulación y al libre intercambio de energía (oceánica y atmosférica) entre los dos hemisferios. La circulación en la zona ecuatorial es, por lo tanto, de este a oeste, tanto en lo que respecta a las corrientes ecuatoriales del norte y del sur como con respecto a los alisios del noreste en el hemisferio norte y del sureste en el hemisferio sur. Por último, lo que se ha denominado abombamiento ecuatorial de los océanos tiene varias consecuencias: entre ellas, la formación de lo que se ha denominado contracorrientes ecuatoriales también del norte y del sur, definidas e identificadas en muchos atlas y libros de geografía y de ciencias de la Tierra, y la desviación hacia las zonas subtropicales y templadas: de nuevo, hacia la derecha en el hemisferio norte y hacia la izquierda en el hemisferio sur.

Efectos de la fuerza de Coriolis

Una de las raras ocasiones en la cual una persona puede sentir la fuerza de Coriolis es cuando trata de caminar siguiendo una trayectoria radial en un tiovivo (o carrusel). Cuando la persona se aleja del eje de rotación, sentirá una fuerza que la empuja en el sentido contrario a la rotación: es la fuerza de Coriolis.⁴ Cuando una persona se aleja o se acerca del eje de rotación a una velocidad de 1 m/s en un tiovivo que gira a 10 vueltas por minuto, la aceleración de Coriolis es:

${\displaystyle a_{c}=2\omega V=2\textstyle {2\pi 10 \over 60}1=2\,m/s^{2}}$

Se trata, por consiguiente, de una aceleración lateral 4,6 veces más pequeña que la gravedad, pero que para una persona de 70 kg, eso corresponde a una fuerza lateral igual al peso de 15 kg. que es perfectamente percibida.

Objetos que se desplazan sobre la Tierra

La Tierra gira mucho más lentamente que un carrusel. Su velocidad angular es de ${\displaystyle \scriptstyle {2\pi }}$ radianes por día sideral (23 h, 56 m, 4,1 s) es decir ${\displaystyle \scriptstyle {7{,}292\,10^{-5}}\,rad/s}$. La aceleración de Coriolis debido a la rotación de la Tierra es mucho menor.

Cuando un cuerpo sigue una trayectoria norte-sur sobre la Tierra (siguiendo un meridiano), la componente radial de su velocidad (la velocidad a la cual el cuerpo se acerca o se aleja del eje de rotación terrestre) depende de la latitud del cuerpo. Es fácil ver que la componente radial es ${\displaystyle \scriptstyle {V_{r}=V_{NS}\sin(\mathrm {latitud} )}}$. Cuando el cuerpo está cerca del ecuador, su distancia respecto al eje de la Tierra no cambia. Si la trayectoria del cuerpo es este-oeste y sigue un paralelo, su distancia respecto al eje terrestre no varía, pero ya hemos visto que sentirá una aceleración de Coriolis dirigida hacia el eje de la Tierra que vale ${\displaystyle \scriptstyle {a_{eje}=2\omega V_{EO}}}$. La componente paralela a la superficie de la Tierra depende de la latitud y es: ${\displaystyle \scriptstyle {a_{c}=2\omega V_{EO}\sin(\mathrm {latitud} )}}$.

Vemos que en los dos casos, visto desde la Tierra, un cuerpo que se desplaza sobre la superficie de la Tierra siente una aceleración lateral de valor ${\displaystyle \scriptstyle {a_{c}=2\omega V\sin(\mathrm {latitud} )}}$ dirigida hacia la derecha de la velocidad.

Un cuerpo que se desplaza con una velocidad de 1 m/s, sin interacción con el suelo, a una latitud de 45° encuentra una aceleración lateral de Coriolis igual a:

${\displaystyle a_{c}=2\cdot 7{,}292\cdot 10^{-5}\sin(45^{\circ })=1{,}03\cdot 10^{-4}\mathrm {m/s} ^{2}}$,

lo cual corresponde a una fuerza lateral aproximadamente 100 000 veces menor que su propio peso. Dicho de otra manera, la trayectoria se desvía hacia la derecha como si el terreno estuviese inclinado hacia la derecha 1 milímetro cada 100 metros.

Si se trata de un avión cuya velocidad es 900 km/h (250 m/s), la aceleración será 250 veces mayor. El efecto será darle al avión una trayectoria circular de 4850 km de diámetro (a una latitud de 45°):

${\displaystyle a_{c}=2\omega V\sin(45^{\circ })=\textstyle {V^{2} \over R}}$

${\displaystyle 2R=\textstyle {V \over \omega \sin(45^{\circ })}=\textstyle {250 \over 7{,}292\cdot 10^{-5}\sin(45^{\circ })}=4{,}846\cdot 10^{6}\ \mathrm {m} }$

Por supuesto, el piloto corregirá esta desviación, pero no parece posible que pueda distinguirla de los efectos del viento o de los errores de reglaje de la posición neutra de los alerones de dirección y de profundidad.

Balística

Tomemos el caso de un obús, situado a una latitud de 45° y que tira un proyectil a 110 km de distancia. El ángulo de tiro para esa distancia es de 45°. Si se desprecia el efecto de los rozamientos con el aire, la velocidad horizontal del proyectil es de 734 m/s, y el tiempo de vuelo es de 150 segundos. La aceleración de Coriolis será:

${\displaystyle a_{c}=2\omega V\sin(\mathrm {latitud} )=7{,}58\cdot 10^{-2}\ \mathrm {m/s} ^{2}}$

La distancia lateral de desvío provocada por la aceleración de Coriolis es:

${\displaystyle d=\textstyle {1 \over 2}a_{c}t^{2}=\textstyle {1 \over 2}7{,}58\cdot 10^{-2}150^{2}=852\ \mathrm {m} }$

Esa distancia corresponde a un error en el ángulo de tiro de 0,44°. Las opiniones divergen sobre la importancia de este error, comparado con la influencia de otras fuerzas y, sobre todo, con la fuerza provocada por el efecto Magnus sobre proyectiles que giran axialmente.

Para cañones de menor alcance, el error en el ángulo de tiro es aún menor. Por ejemplo, para un proyectil cuyo alcance es de 20 km y cuya velocidad media es la misma, el error del ángulo es 25 veces menor.

Efecto Eötvös

La versión simplificada del efecto Coriolis esta ligada a su componente horizontal causada por movimientos horizontales con respecto a la superficie terrestre.

Pero también hay componentes verticales del efecto Coriolis que son significativos. Los objetos que viajen hacia el este a gran velocidad se desviarán hacia arriba (parecerán más ligeros), mientras que los que lo hagan hacia el oeste se desviarán hacia abajo (parecerán más pesados). Esto se conoce como el efecto Eötvös. Este componente vertical del efecto Coriolis es mayor en el ecuador, y se reduce a cero en los polos.

Otro caso a tener en cuenta es el de objetos que viajan en dirección perpendicular al eje de rotación. Aquellos que se desplacen arriba a gran velocidad se desviarán hacia el oeste y los que lo hagan hacia abajo se desviarán hacia el este. El efecto de nuevo alcanza su máximo en el ecuador y es 0 en los polos (en el ecuador un movimiento vertical es perpendicular al eje de rotación y en los polos sin embargo es paralelo y por lo tanto el efecto causado por Coriolis en ese caso es 0).

Explicación intuitiva

Imaginemos un tren que viaja por una vía sin rozamiento alrededor del ecuador de la Tierra a la velocidad necesaria para completar una vuelta al mundo en un día (465 m/s).⁵ Analizamos el efecto Coriolis en tres casos:

• 1. Cuando se desplaza hacia el oeste.
• 2. Cuando esta en reposo.
• 3. Cuando se desplaza hacia el este.

Para cada uno de estos casos calculamos el efecto Coriolis, primero desde el punto de vista de nuestro sistema de referencia en rotación en la Tierra para a continuación comprobar que el resultado es el mismo observando el tren en un sistema de referencia inercial. En la siguiente imagen podemos observar los tres casos en el sistema de referencia inercial vistos desde un punto fijo sobre la tierra en su eje de rotación:

1. El tren viaja hacia el oeste: En este caso el movimiento es en dirección contraria a la de rotación, por lo tanto en el sistema de referencia en rotación de la tierra el término causado por el efecto Coriolis está dirigido hacia el eje de rotación, en el ecuador esto es hacia abajo, aplicando la fórmula del efecto Coriolis el tren y sus pasajeros deberían ser más pesados mientras se desplazan hacia el oeste.

• Si observamos el tren en el sistema de referencia inercial desde el punto fijo sobre el Polo Norte, observamos que a esa velocidad este se mantiene inmóvil mientras que la Tierra rota bajo el tren, por tanto la única fuerza que actúa sobre el tren es la gravedad y la fuerza de reacción de las vías. Esta fuerza es mayor (un 0,34%)⁵ que la fuerza total resultante experimentada por el tren cuando esta en reposo (y rotando junto con la Tierra). El efecto Coriolis permite explicar esta diferencia en nuestro sistema de referencia en rotación.

2. El tren se para: Desde nuestro punto de vista en la tierra (sistema de referencia en rotación) la velocidad del tren es 0 y por tanto la fuerza derivada de Coriolis es también 0 por lo que tanto el tren como sus pasajeros recuperan su peso normal.

• Desde el punto de vista fijo sobre la Tierra en el sistema de referencia inercial, el tren gira en este caso junto con el resto de la Tierra. Un 0,34 por ciento de la fuerza de la gravedad aporta la fuerza centripeta necesaria para conseguir el movimiento circular en ese sistema de referencia. El resto de la fuerza que se podría medir usando una báscula, causaría que el tren y sus pasajeros fueran más ligeros que en el caso anterior.

3. El tren cambia su dirección y viaja hacia el este. En este caso al moverse en la misma dirección que la rotación terrestre, el efecto de Coriolis estará dirigido hacia fuera del eje de rotación, es decir, hacia arriba. Esta fuerza causará que el tren y sus pasajeros registren un menor peso que cuando se encontraban en reposo.

Gráfico de la fuerza experimentada por un objeto de 10 kilogramos en función de su velocidad de desplazamiento por el ecuador terrestre (dentro del sistema de referencia en rotación). (Los valores positivos en el eje de fuerza están dirigidos hacia arriba. Los valores positivos en el eje de velocidad están dirigidos hacia el este y los negativos hacia el oeste).

• Visto desde el espacio, en el sistema de referencia inercial el tren al viajar hacia el este sumará su velocidad a la de la tierra y por tanto se verá girando al doble de velocidad que cuando estaba en reposo y por tanto la cantidad de fuerza centrípeta necesaria para mantener el movimiento circular es mayor reduciendo la fuerza neta actuando sobre las vías hacia el centro de la tierra. Esta diferencia de fuerza es la explicada anteriormente por el término de Coriolis en sistema de referencia en rotación.
• Como comprobación final podemos imaginar al propio tren como sistema de referencia en rotación. Ya que el sistema rota al doble de velocidad angular que el de la tierra el componente de fuerza centrífuga en dicho sistema de referencia es mayor que el de la tierra y al estar los pasajeros en reposo en dicho sistema este sería el único componente adicional, explicando de nuevo que el tren y sus pasajeros sean más ligeros que en los dos casos anteriores.

Esto explica por que los proyectiles a alta velocidad que se disparan hacia el este se desvían hacia arriba mientras que si son disparados hacia el oeste la desviación es hacia abajo. Esta componente vertical del efecto de Coriolis se denomina el Efecto Eötvös.⁶

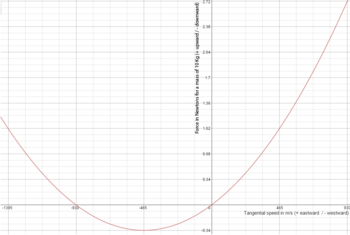
Podemos usar el ejemplo para explicar por que el efecto Eötvös comienza a reducirse en objetos que viajan hacia el oeste una vez que su velocidad tangencial supera la velocidad de rotación de la tierra (465 m/s en el ecuador). Si el tren que viaja hacia el oeste en el ejemplo incrementa su velocidad en esa dirección y lo observamos desde el sistema de referencia inercial en el espacio veremos que empieza a rotar alrededor de la tierra que gira debajo en dirección contraria. Para mantener esa trayectoria circular, parte de la fuerza de la gravedad que empuja al tren contra las vías actuaría como fuerza centrípeta. Una vez que el tren doblara su velocidad a 930 m/s la fuerza centrípeta sería igual a la experimentada cuando el tren se encuentra parado. Desde el punto de vista del sistema de referencia inercial en ambos casos el tren está rotando a la misma velocidad (465 m/s) solo que en direcciones opuestas. Por lo tanto la fuerza es la misma y por tanto el efecto Eötvös se cancelaría completamente a esa velocidad. Cualquier objeto que se mueva hacia el oeste a una velocidad superior a 930 m/s no experimentara una desviación hacia abajo, si no hacia arriba. El gráfico de la derecha ilustra la fuerza causada por el efecto Eötvös que experimentaría un objeto de 10 gramos en el tren del ejemplo en función de su velocidad. La forma parabólica del gráfico se explica porque la fórmula de la fuerza centrípeta es proporcional al cuadrado de la velocidad tangencial. En el sistema de referencia inercial la parte de abajo de la parábola estaría centrada en el origen. El desplazamiento del origen se explica porque estamos usando el sistema de referencia en rotación de la tierra. Observando el gráfico podemos comprobar que el efecto Eötvös no es simétrico, y que la fuerza hacia abajo experimentada por un objeto viajando hacia el oeste a gran velocidad es menor que la fuerza hacia arriba experimentada por el mismo objeto viajando en dirección al este a la misma velocidad.

Aplicación práctica

Una aplicación práctica de la fuerza de Coriolis es el caudalímetro másico, un instrumento que mide el caudal másico de un fluido que circula a través de una tubería. Este instrumento fue comercializado en 1977 por Micro Motion Inc.

Los caudalímetros normales miden el caudal volumétrico, el cual es proporcional al caudal másico sólo cuando la densidad del fluido es constante. Si el fluido tiene una variación de densidad o contiene burbujas, entonces el caudal volumétrico, multiplicado por la densidad, no será exactamente igual al caudal másico. El caudalímetro másico de Coriolis funciona aplicando una fuerza de vibración a un tubo curvado a través del cual pasa el fluido. El efecto Coriolis crea una fuerza en el tubo perpendicular a ambas direcciones: la de vibración y la dirección de la corriente. Esta fuerza se mide para obtener el caudal másico. Los caudalímetros de Coriolis pueden usarse además con fluidos no newtonianos, en los cuales los caudalímetros normales tienden a dar resultados erróneos. El mismo instrumento puede usarse para medir la densidad del fluido. Este instrumento tiene una novedad adicional, que consiste en que el fluido está en un tubo liso, sin partes móviles, que no necesita limpieza ni mantenimiento y presenta una caída de presión muy baja.

El efecto Eötvös es el cambio en la fuerza de la gravedad medida causado por el cambio en la aceleración centrífuga resultante del movimiento en dirección este u oeste del punto desde el que se efectúa la medida. Cuando el punto de observación se mueve hacia el este, la velocidad angular del objeto se incrementa (sumándose a la de rotación de la Tierra), y por lo tanto la fuerza centrífuga también aumenta, causando una reducción en la medición de la fuerza de gravedad.

Descubrimiento del efecto Eötvös

A principios de la década de 1900, un equipo alemán del Instituto de Geodesia de Potsdam realizó mediciones de la gravedad en buques en movimiento en los océanos Atlántico, Índico y Pacífico. Estudiando los resultados obtenidos, el físico húngaro Loránd Eötvös (1848-1919) se dio cuenta de que las lecturas fueron menores cuando el barco se movía hacia el este, y más altas cuando se movía hacia el oeste. Este hecho se identificó como una consecuencia de la rotación de la Tierra. En 1908, se realizaron nuevas mediciones en el Mar Negro con dos barcos: uno se movía hacia el este y el otro hacia el oeste. Los resultados obtenidos coincidían con las deducciones de Eötvös.¹

Explicación física

El diseño más común de un gravímetro concebido para el trabajo de campo está basado en un muelle: algo tan simple como un resorte del que se suspende un peso interno. La fuerza de suspensión proporcionada por el muelle contrarresta la fuerza de la gravedad. Un resorte así fabricado tiene la propiedad de que la cantidad de fuerza que ejerce el resorte es proporcional a la extensión del muelle respecto a su longitud inicial (es decir, cuando no está cargado). Cuanto más fuerte es la gravedad efectiva en una ubicación particular, más se extiende el resorte: el muelle se extiende en la longitud necesaria para contrarrestar el efecto de la gravedad sobre el peso interno. Las partes móviles del gravímetro se montan en cápsulas rellenas de líquido para que el dispositivo sea menos susceptible a las influencias externas, tales como las vibraciones y los cambios de temperatura.

Formulación

Fórmula general

Desde entonces, en geodesia se utiliza la fórmula siguiente para corregir el efecto de la velocidad respecto a la Tierra durante una serie de mediciones:²

${\displaystyle a_{r}=2\cdot \Omega \cdot u\cdot \cos \phi +{\frac {u^{2}+v^{2}}{R}}}$

siendo:

${\displaystyle \Omega }$ = la velocidad angular de rotación de la Tierra

${\displaystyle u}$ = la velocidad en la dirección latitudinal (este-oeste)

${\displaystyle \phi }$ = la latitud en la que se toman las mediciones

${\displaystyle v}$ = la velocidad en la dirección longitudinal (norte-sur)

${\displaystyle R}$ = el radio de la Tierra

El primer término de la fórmula, ${\displaystyle (2\cdot \Omega \cdot u\cdot \cos \phi )}$, corresponde al efecto Eötvös. El segundo término es un refinamiento que en circunstancias normales es mucho menor que el efecto Eötvös.

Primer término

El primer término de la fórmula del efecto Eötvös es proporcional a la componente de la fuerza centrípeta perpendicular a la superficie local de la Tierra (ligada a la latitud), y por lo tanto es descrita por una ley coseno: cuanto más cerca de la línea ecuatorial, mayor es la distancia al eje de la tierra (radio de giro) y más fuerte será el efecto.

Fuerza de gravedad, fuerza normal y su resultante

La deducción matemática del efecto Eötvös para el movimiento a lo largo de la línea del Ecuador, explica el factor 2 en el primer término de la fórmula (ver en el punto siguiente el desarrollo de la fórmula simplificada).

Debido a su rotación, la Tierra es de forma casi esférica (presentando un ligero abombamiento ecuatorial, que en este caso no se considera). La fuerza de gravedad se dirige hacia el centro de masas de la Tierra, y la fuerza normal es perpendicular a la superficie local.

En los polos y en el ecuador, la fuerza de la gravedad y la fuerza normal tienen exactamente la dirección opuesta. En todas las demás latitudes, las dos fuerzas no son exactamente opuestas, por lo que queda una fuerza resultante, que actúa hacia el eje de la Tierra. En cada latitud es precisamente la cantidad de fuerza centrípeta necesaria para mantener un espesor uniforme de la capa atmosférica. Por otro lado, la Tierra sólida es dúctil. Siempre que la forma de la Tierra sólida no está del todo en equilibrio con su velocidad de rotación, entonces un esfuerzo cortante la deforma en un período de millones de años hasta que se recupera el equilibrio.

Cuando una aeronave tiene una velocidad hacia el este (a favor del giro de la Tierra), adquiere un "exceso de velocidad". La situación es comparable a la de un coche de carreras en un velódromo con una superficie muy resbaladiza. Si el coche de carreras va demasiado rápido, entonces el coche tiende a salirse de la pista hacia arriba. Para una aeronave en vuelo, esto equivale a una reducción del peso, en comparación con el peso cuando la aeronave está en reposo con respecto a la Tierra.

Si a continuación la aeronave tiene una velocidad hacia el oeste, la situación es como la de un coche de carreras en un velódromo cuando va demasiado lento: en una superficie resbaladiza el coche va a desplomarse hacia abajo. Para una aeronave en vuelo esto significa un aumento del peso.

Segundo término

El segundo término representa la aceleración centrípeta requerida para que la aeronave siga la curvatura de la tierra. Es independiente tanto de la rotación de la Tierra como de la dirección del movimiento. Por ejemplo, cuando un avión que lleva instrumentos de lectura gravimétricos sobrevuela uno de los polos con altitud constante, la trayectoria del avión sigue la curvatura de la tierra. El primer término de la fórmula es cero, debido a que el coseno del ángulo es cero (en los polos ${\displaystyle \cos \phi =\cos 90=0}$); entonces el segundo término representa la aceleración centrípeta necesaria para seguir la curvatura de la superficie de la Tierra a una velocidad dada.

Fórmula simplificada

Para un objeto en movimiento sobre el ecuador: Un sistema de referencia conveniente en esta situación es un sistema de coordenadas inercial que se desplace con el centro de masas de la Tierra. En esta situación, se puede afirmar que los objetos que están en reposo sobre la superficie de la Tierra (es decir, que giran conjuntamente con la Tierra), están dando vueltas eje de la Tierra, por lo que experimentan la correspondiente aceleración centrípeta con respecto a este sistema inercial de coordenadas.

Lo que se pretende determinar es la diferencia de la aceleración centrípeta de la aeronave cuando no se desplaza respecto a la Tierra, y cuando tiene una velocidad con respecto a la misma. La siguiente deducción es válida exclusivamente para el movimiento en dirección este-oeste (o también en dirección oeste-este, de signo contrario).

Notación:

${\displaystyle a_{u}}$ es la aceleración centrípeta total cuando la aeronave se mueve a lo largo de la superficie de la Tierra.

${\displaystyle a_{s}}$ es la aceleración centrípeta cuando la aeronave permanece estacionaria con respecto a la Tierra.

${\displaystyle \Omega }$ es la velocidad angular de la Tierra: una revolución por día sideral.

${\displaystyle \omega _{r}}$ es la velocidad angular de la aeronave relativa a la velocidad angular de la Tierra.

${\displaystyle (\Omega +\omega _{r})}$ es la velocidad angular total de la aeronave.

${\displaystyle \omega _{r}*R=u}$ es la velocidad de la aeronave (velocidad relativa a la Tierra).

${\displaystyle R}$ es el radio de la Tierra.

Igualando fuerzas y operando, se tiene que:

${\displaystyle {\begin{aligned}a_{r}&=a_{u}-a_{s}\\a_{r}&=(\Omega +\omega _{r})^{2}R-\Omega ^{2}R\\a_{r}&=\Omega ^{2}R+2\Omega \omega _{r}R+\omega _{r}^{2}R-\Omega ^{2}R\\a_{r}&=2\Omega \omega _{r}R+\omega _{r}^{2}R\\a_{r}&=2\Omega u+u^{2}/R\\\end{aligned}}}$

Se puede ver fácilmente que en el caso de movimiento a lo largo del ecuador, la fórmula general se simplifica en la fórmula anterior:

${\displaystyle a_{r}=2\Omega u\cos \phi +{\frac {u^{2}+v^{2}}{R}}=2\Omega u+u^{2}/R}$

(para ${\displaystyle v=0}$ y ${\displaystyle \phi =0}$)

Ejemplo práctico

Se va a calcular la magnitud del efecto Eötvös sobre unas mediciones de gravedad, suponiendo que:

Caso simplificado

Movimiento sobre el ecuador:

-La masa interna del gravímetro es de 10 kilogramos

-El gravímetro se desplaza en un dirigible sobrevolando el [Ecuador terrestre], con una velocidad de crucero uniforme de 25 metros por segundo (se desprecia la altura del dirigible)

Gráfico de la fuerza experimentada por un objeto de 10 kilogramos en función de su velocidad de desplazamiento por el ecuador terrestre (dentro del sistema de referencia en rotación). (Los valores positivos en el eje de fuerza están dirigidos hacia arriba. Los valores positivos en el eje de velocidad están dirigidos hacia el este y los negativos hacia el oeste).

Cálculo: En el ecuador, la velocidad de la superficie de la Tierra es de unos 465 metros por segundo (una vuelta completa por el ecuador cada 24 horas: aproximadamente 40000000m/24h/60m/60s). La aceleración centrípeta ${\displaystyle a_{n}}$ resultante del giro de la Tierra, con un radio de 6378 kilómetros (radio ecuatorial de la Tierra) de la trayectoria circular del dirigible, es de:

${\displaystyle a_{n}={\frac {v^{2}}{R}}={\frac {{465}^{2}}{6378000}}=0.034m/s^{2}}$

o lo que es equivalente, es de aproximadamente 0.034 newton por kilogramo de masa. Para la masa de 10 kg, el efecto de la fuerza centrípeta asciende a aproximadamente 0.34 newton. La fuerza necesaria para mantener en suspensión la masa de la pesa interna de 10 kg (es decir, la lectura del gravímetro), se determina tomando la atracción gravitatoria (multiplicado la masa por la aceleración de la gravedad, que en este ejemplo se considera ${\displaystyle g=10m/s^{2}}$) de 100 newtons, y restándole esos 0.34 newtons. En otras palabras: cualquier objeto que gira conjuntamente con la Tierra en el ecuador, tiene su peso medido reducido en un 0.34 por ciento, debido a la rotación de la Tierra.

Cuando se circula a 25m/s hacia el este, la velocidad total se convierte en 465+25=490m/s, lo que requiere una fuerza centrípeta de cerca de 0.375 newton (repitiendo el cálculo anterior, pero con v=490m/s). Cuando se circula a 25m/s hacia el oeste, la velocidad total se convierte en 465-25=440m/s, lo que requiere unos 0.305 newtons. En consecuencia, después de girar 180º, la lectura del gravímetro variará en un 0.7% (unos 7 gramos para la masa de 10 kg). En consecuencia, el muelle del gravímetro deberá extenderse un poco para acomodar un "peso" ligeramente mayor.

Caso general

Movimiento a lo largo del paralelo a 60 grados de latitud:

Efecto Eötvös para un objeto que se mueve hacia el este a lo largo de 60 grados de latitud. El objeto tiende a alejarse del eje de la Tierra

Efecto Eötvös para un objeto que se mueve hacia el oeste a lo largo de 60 grados de latitud. El objeto tiende a acercarse hacia el eje de la Tierra

Se utiliza de nuevo el mismo gravímetro, con una masa interna de 10 kilogramos.

Cálculo de la reducción de peso en situación estacionaria respecto a la Tierra:
Un objeto situado a 60 grados de latitud, con el mismo movimiento que la Tierra, está siguiendo una trayectoria circular, con un radio de unos 3.190 kilómetros, y una velocidad de aproximadamente 233m/s (dado que ${\displaystyle \cos \phi =\cos 60=0.5}$, el radio es la mitad que el ecuatorial, y la velocidad también se reduce a la mitad que en el caso anterior, cuando el objeto estaba en el ecuador). Esa trayectoria circular requiere una fuerza centrípeta de alrededor de 0.017 newton por cada kilogramo de masa (${\displaystyle a_{n}}$=233^2//3190000 = 0.17 m/s2) ; o lo que es lo mismo, 0.17 newton para el peso interno de 10 kilogramos. A los 60 grados de latitud, la componente de la aceleración centrípeta perpendicular a la superficie local (la vertical local) es la mitad de la fuerza total (otra vez interviene el coseno de 60º). Por lo tanto, a 60 grados de latitud, cualquier objeto en movimiento con la Tierra tiene su peso (inicialmente 100 newtons) reducido en aproximadamente un 0,08 por ciento (= 0.17 · cos 60), debido a la rotación de la Tierra.

Cálculo del efecto de Eötvös:
Cuando la aeronave se desplazaba a 25m/s hacia el este, la velocidad total se convierte en 233+25=258m/s, lo que requiere una fuerza centrípeta de cerca de 0.208 newton. Debido al coseno de 60º, la componente vertical local resultante es la mitad: 0.104 newton. Cuando la aeronave se desplazaba a 25m/s hacia el oeste, la velocidad total se convierte en 233-25=208m/s, lo que se traduce en una fuerza centrípeta de cerca de 0.135 newton. La componente vertical local resultante también es la mitad: 0.068 newton. De aquí se deduce que a 60 grados de latitud, la diferencia de peso de la masa de 10 kilogramos antes y después del cambio de sentido de la aeronave es de 1.7 gramos en el peso medido (de forma aproximada, la fuerza gravitatoria con la que la Tierra atrae una masa de un gramo -peso- equivale a un newton).

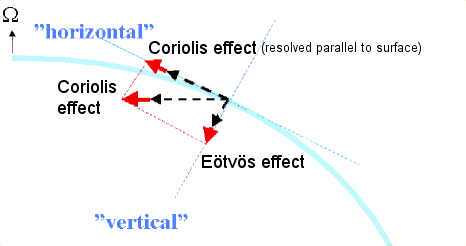
Los diagramas muestran también la componente tangente a la superficie local. En meteorología y en oceanografía, es habitual referirse a los efectos de la componente paralela a la superficie local como efecto Coriolis.

Otras aplicaciones

En meteorología, en modelos de alto rendimiento, se debe tener en cuenta el efecto Eötvos a escala terrestre. Las masas de aire pueden tener velocidades considerables con respecto a la superficie terrestre, lo que puede traducirse en una tendencia del aire a migrar a mayor altitud, lo que debe tenerse en cuenta cuando las exigencias de precisión son máximas.