Geometría elemental

Ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto a este. También se la conoce como transversal angular.

Se puede decir que la mediana, la altura y la bisectriz son cevianas o rectas notables de un triángulo. ¹

El nombre de ceviana fue introducido por M.A. Poulain, que lo utilizó en honor de Giovanni Ceva, quien en 1678 había formulado el teorema que lleva su nombre, Teorema de Ceva publicándolo en su artículo De lineis rectis se invicem secantibus statica constructio. Este teorema da la condición necesaria y suficiente para que tres cevianas se corten en un punto.

Triángulo con una ceviana d.

CIRCUNFERENCIA CEVIANA
La circunferencia ceviana de un punto respecto de un triángulo es la circunferencia circunscrita a su triángulo ceviano.

cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, denominada directriz del cilindro.

Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.

En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.

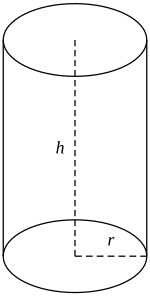
Un cilindro circular recto.

Clasificación

Un cilindro puede ser:

• cilindro rectangular: si el eje del cilindro es perpendicular a las bases.
• cilindro oblicuo: si el eje no es perpendicular a las bases.
• cilindro de revolución: si está limitado por una superficie que gira 360° grados.

Superficie cilíndrica

La superficie cilíndrica está conformada por rectas paralelas, denominadas generatrices, las cuales contienen los puntos de una curva plana, denominada directriz del cilindro. La superficie lateral cilíndrica se obtiene mediante el giro de una recta alrededor de un eje.

Las superficies cilíndricas pueden ser

• superficie cilíndrica de revolución: si todas las generatrices equidistan de un eje, paralelo a ella,
• superficie cilíndrica de no revolución: si no existe un eje que equidiste de las generatrices.

Área de la superficie cilíndrica

La superficie de un cilindro circular recto está conformada por el área de la base, circular en este caso: A = π r², pero como este cilindro tiene 2 bases se multiplica por 2, siendo el área total de las dos bases: A_b = 2 π r²

Además, el área lateral está formada por un rectángulo de altura "h" y de largo del perímetro del círculo L = 2 π r por lo que el área lateral es: A_l = 2 π r h

Por lo tanto, el área total, o área de la superficie cilíndrica es:

A = A_b + A_l

A = 2 π r² + 2 π r h

A = 2 π ( r² + r h )

A = 2 π r ( r + h )

Volumen del cilindro

El volumen de un cilindro es el producto del área de la base "A_b" por la altura del cilindro "h"

El volumen de un cilindro de base circular, es:

V = π r ²·h

Siendo la altura del cilindro la distancia entre las bases.

Cilindro como superficie cuádrica

Las secciones cónicas son de tres tipos: elipses, parábolas e hipérbolas, que sirviendo de directrices, originan tres tipos de superficies cuádricas cilíndricas:

Cilindro elíptico

Tomando como directriz una elipse, se puede generar una superficie cilíndrica elíptica (que incluye a los cilindros circulares, cuando los semiejes de la elipse son iguales).

En un sistema ortogonal de coordenadas, tomando como eje z una recta cuya dirección es paralela a la generatriz, si se escoge como origen el centro de simetría, la ecuación de la superficie cilíndrica es similar a la de la superficie cónica correspondiente.

La ecuación de un cilindro elíptico es de la forma:

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}$

donde a y b son los semiejes.

Cilindro parabólico

En similares condiciones, la ecuación de una superficie parabólica será de la forma:

${\displaystyle y=x^{2}\,}$

Cilindro hiperbólico

En similares condiciones, la ecuación de un superficie hiperbólica es de la forma:

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

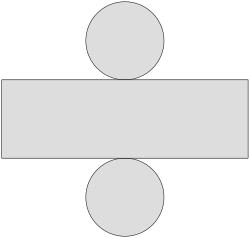
El área del cilindro es la suma del área de las dos bases circulares más el área lateral.

Siendo A_b=2·π·r² el área de las bases y A_l=2·π·r·h el área lateral, sumando tenemos:

Volumen del cilindro

ANUNCIOS

El volumen del cilindro es: