Termodinámica

Números adimensionales usados en termodinámica

El número de Eckert (Ec) es un número adimensional utilizado en mecánica de fluidos. Expresa la relación entre la energía cinética de un fluido y su entalpía. Su nombre es en honor del profesor Ernst R. G. Eckert.

Se define como:

${\displaystyle {\mathit {Ec}}={\frac {V^{2}}{c_{p}\Delta T}}={\frac {\mbox{Energia Cinetica}}{\mbox{Entalpia}}}}$

En donde:

• ${\displaystyle V}$ es la velocidad característica del fluido.
• ${\displaystyle c_{p}}$ es la capacidad calorífica a presión constante del fluido.
• ${\displaystyle \Delta T}$ es la diferencia de temperaturas característica del fluido.

En la física y en ingeniería mecánica, la eficacia energética (o eficacia termodinámica) es un número sin dimensión, que es el informe que indica lo que puede recuperarse provechosamente de la máquina de lo que se ha gastado para hacerla funcionar.

La eficacia energética se denomina con la letra griega eta, y se define como

${\displaystyle \mathrm {eficiencia} \ \eta =\mathrm {{salida} \over \mathrm {entrada} } }$

Donde salida (output) es la cantidad de trabajo mecánico (en vatios) o energía consumida por el proceso (en julios), y entrada (input), es la cantidad de trabajo ó energía que se utiliza como entrada para efectuar el proceso.

Este concepto muy a menudo se confunde con el rendimiento, que es la relación entre la eficacia real de la máquina y la eficacia teórica máxima que se puede esperar de ella. El rendimiento tiene siempre un valor incluido entre 0 y 1 (o 0 y 100.%), mientras que según el sistema, la eficacia puede tomar cualquier valor positivo.¹

En economía, el término de eficacia energética se utiliza de manera sinónima al de eficiencia energética, que consiste en reducir los consumos de energía a igual servicio prestado.

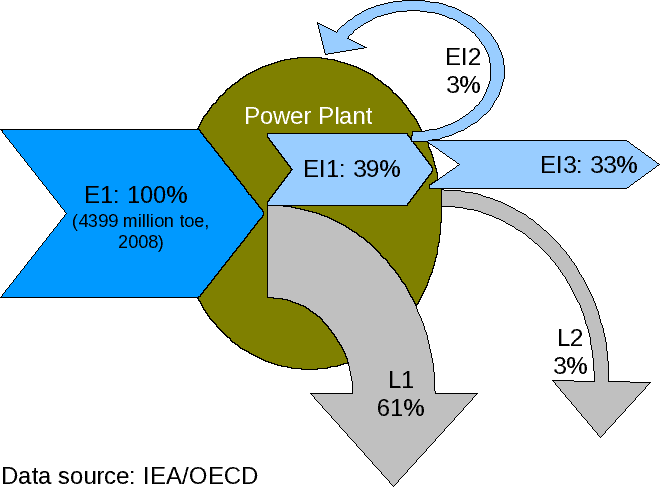
Eficacia energética de Generación de energía eléctrica, 2008

Número de Fourier (Fo) o Módulo de Fourier, llamado así en honor a Joseph Fourier, es un número adimensional que caracteriza la conducción de calor. Conceptualmente es la relación entre la velocidad de la conducción de calor y la velocidad del almacenamiento de energía. Se define como:

${\displaystyle {\mbox{Fo}}={\frac {\alpha t}{L^{2}}}}$

En donde:

• α es la difusividad térmica.
• t es el tiempo característico.
• L es la longitud a través de la que la conducción de calor ocurre.

Ley de Fourier

Sea J la densidad de corriente de energía (energía por unidad de área y por unidad de tiempo), que se establece en la barra debido a la diferencia de temperaturas entre dos puntos de la misma. La ley de Fourier afirma que hay una proporcionalidad entre el flujo de energía J y el gradiente de temperatura.

J=K∂T∂x${\displaystyle J=K\frac{\partial T}{\partial x}}$

Siendo K una constante característica del material denominada conductividad térmica.

Consideremos un elemento de la barra de longitud dx y sección S. La energía que entra en el elemento de volumen en la unidad de tiempo es JS, y la que sale es J’S. La energía del elemento cambia, en la unidad de tiempo, en una cantidad igual a la diferencia entre el flujo entrante y el flujo saliente.

JS−J'S=−∂J∂xS dx${\displaystyle JS-J\text{'}S=-\frac{\partial J}{\partial x}Sdx}$

Esta energía, se emplea en cambiar la temperatura del elemento. La cantidad de energía absorbida o cedida (en la unidad de tiempo) por el elemento es igual al producto de la masa de dicho elemento por el calor específico y por la variación de temperatura.

(ρ Sdx)c∂T∂t${\displaystyle \left(\rho Sdx\right)c\frac{\partial T}{\partial t}}$

Igualando ambas expresiones, y teniendo en cuenta la ley de Fourier, se obtiene la ecuación diferencial que describe la conducción térmica

∂T∂t=α∂2T∂x2  α=Kρ c${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\alpha =\frac{K}{\rho c}}$

Solución analítica

Supongamos una barra metálica de longitud L, conectada por sus extremos a dos focos de calor a temperaturas T_ay T_b respectivamente. Sea T₀ la temperatura inicial de la barra cuando se conectan los focos a los extremos de la barra.

Al cabo de cierto tiempo, teóricamente infinito, que en la práctica depende del tipo de material que empleamos, se establece un estado estacionario en el que la temperatura de cada punto de la barra no varía con el tiempo. Dicho estado está caracterizado por un flujo J constante de energía. La ley de Fourier establece que la temperatura variará linealmente con la distancia x al origen de la barra.

Ta+Tb−TaLx${\displaystyle T_a+\frac{T_b-T_a}{L}x}$

Para describir el estado transitorio buscamos una solución de la forma T(x, t)=F(x)·G(t), variables separadas

∂T(r,t)∂t=α∂2T(r,t)∂2x1α1G(t)dG(t)dt=1F(x)d2F(x)d2x=−ω2${\displaystyle \begin{array}{l}\frac{\partial T(r,t)}{\partial t}=\alpha \frac{{\partial }^{2}T(r,t)}{{\partial }^{2}x}\\ \frac{1}{\alpha }\frac{1}{G(t)}\frac{dG(t)}{dt}=\frac{1}{F(x)}\frac{d^{2}F(x)}{d^{2}x}=-{\omega }^2\end{array}}$

El signo negativo asegura el carácter transitorio.

Integramos la primera ecuación diferencial

dG(t)dt+αω2G(t)=0G(t)=G(0)⋅exp(−αω2t)${\displaystyle \begin{array}{l}\frac{dG(t)}{dt}+\alpha {\omega }^{2}G(t)=0\\ G(t)=G(0)·\exp (-\alpha {\omega }^{2}t)\end{array}}$

Integramos la segunda ecuación diferencial

d2F(x)d2x+ω2F(x)=0${\displaystyle \frac{d^{2}F(x)}{d^{2}x}+{\omega }^{2}F(x)=0}$

Es una ecuación diferencial similar a la de un MAS, cuya solución es a·sen(ωx+δ)

La temperatura en cualquier punto x a lo largo de la barra, en un instante determinado, T(x, t) es la solución de la ecuación diferencial, que es una combinación de dos términos, la que corresponde al régimen permanente más la del régimen transitorio.

T(x,t)=Ta+Tb−TaLx+∑n=1∞anexp(−αω2nt)sin(ωnx+δn)${\displaystyle T(x,t)=T_a+\frac{T_b-T_a}{L}x+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\omega }_{n}x+{\delta }_n\right)}$

Condiciones de contorno

• En x=0, T(0, t)=T_a, temperatura fija del extremo izquierdo de la barra

0=∑n=1∞anexp(−αω2nt)sin(δn)  δn=0${\displaystyle 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\delta }_n\right){\delta }_n=0}$

• En x=L, T(L, t)=T_b, temperatura fija del extremo derecho de la barra

0=∑n=1∞anexp(−αω2nt)sin(ωnL)   ωnL=nπ${\displaystyle 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\text{sin(}{\omega }_{n}L){\omega }_{n}L=n\pi }$

El régimen variable general de temperaturas de la barra es

T(x,t)=Ta+Tb−TaLx+∑n=1∞anexp(−αn2π2L2t)sin(nπLx)${\displaystyle T(x,t)=T_a+\frac{T_b-T_a}{L}x+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\sin \left(\frac{n\pi }{L}x\right)}$

Distribución inicial de temperaturas

Solamente, queda por determinar los coeficientes a_n, identificando esta solución con la distribución inicial de temperaturas en la barra T(x, 0)=T₀ en el instante t=0.

T(x,0)=Ta+Tb−TaLx+∑n=1∞ansin(nπLx)f(x)=∑n=1∞ansin(nπLx)    f(x)= T0−Ta−Tb−TaLx${\displaystyle \begin{array}{l}T(x\mathrm{,0})=T_a+\frac{T_b-T_a}{L}x+{\displaystyle \sum _{n=1}^{\infty }{a}_n}\sin \left(\frac{n\pi }{L}x\right)\\ f(x)={\displaystyle \sum _{n=1}^{\infty }{a}_n}\sin \left(\frac{n\pi }{L}x\right)f(x)=T_0-T_a-\frac{T_b-T_a}{L}x\end{array}}$

Más abajo, se proporcionan los detalles del cálculo de los coeficientes a_n del desarrollo en serie al lector interesado.

La temperatura en cualquier punto de la barra x, en un instante t, se compone de la suma de un término proporcional a x, y de una serie rápidamente convergente que describe el estado transitorio.

T(x,t)=Ta+Tb−TaLx+∑n=1∞anexp(−αn2π2L2t)sin(nπLx)  an={2nπ(2T0−Ta−Tb) n impar2nπ(Tb−Ta)  n par${\displaystyle T(x,t)=T_a+\frac{T_b-T_a}{L}x+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp \left(-\alpha \frac{n^2{\pi }^2}{L^2}t\right)}\sin \left(\frac{n\pi }{L}x\right)a_n=\{\begin{array}{l}\frac{2}{n\pi }(2T_0-T_a-T_b)n\text{ impar}\\ \frac{2}{n\pi }(T_b-T_a)n\text{ par}\end{array}}$

El valor de α=K/(ρc) nos da una medida de la rapidez con la que el sistema alcanza el estado estacionario. Cuanto mayor sea α antes se alcanza el estado estacionario