Algoritmo de avance-retroceso
Introducción[editar]
Uno de los problemas básicos de los Modelos Ocultos de Márkov es el cálculo de la probabilidad de una secuencia de observables dado un modelo . El objetivo es por tanto calcular eficientemente .
Probabilidad de una secuencia de estados
Supongamos una secuencia de estados . La probabilidad de esta secuencia es:
Probabilidad de una secuencia de observables dada una secuencia de estados
La probabilidad de observar cuando se da precisamente esta secuencia de estados es:
Cada corresponde con el valor de
Probabilidad de una secuencia de observables dado un modelo
Por tanto, para obtener la probabilidad de una secuencia de observables dado un modelo , deberíamos calcular la probabilidad de para cada una de las secuencias posibles .
El cálculo de tal y como se muestra es impracticable; sólo para estados y observaciones sería necesario realizar del orden de operaciones. Para reducir esta complejidad se emplean estrategias de programación dinámica como los algoritmos forward y backward.
Se recomienda revisar la formalización habitual de un Modelo Oculto de Márkov para comprender cada uno de los elementos en la formulación de estos dos procedimientos.
Procedimiento hacia adelante[editar]
Cálculo de [editar]
Consideramos la variable como:
Dado el modelo , es la probabilidad de observar y estar en el instante de tiempo en el estado .
Cálculo hacia adelante de la probabilidad de una secuencia de observaciones.
Inicialización
Recurrencia
,
Terminación
Ejemplo de cálculo de [editar]
El esquema muestra los estados y probabilidades necesarias para el cálculo de :
Cálculo hacia atrás[editar]
Cálculo de [editar]
Consideramos la variable .
Dado el modelo , es la probabilidad de la secuencia de observación desde el instante de tiempo hasta el final, cuando el estado en el instante de tiempo es .
Inicialización
,
Recurrencia
,
,
Terminación
Ejemplo de cálculo de [editar]
El esquema muestra los estados y probabilidades necesarios para el cálculo de para un modelo de 5 estados y una secuencia de observaciones de longitud 5.
Complejidad computacional[editar]
Tanto el procedimiento hacia adelante como el algoritmo backward, requieren del orden de operaciones; muy inferior a operaciones ( es el número de estados y es la longitud de la secuencia de observaciones) que son necesarias si se calcula para todas las posibles secuencias del modelo.
El cálculo de los servirán - junto a los - para contestar las otras dos preguntas fundamentales de los Modelos Ocultos de Márkov:
- ¿Cuál es la secuencia óptima de estados dado una secuencia de observaciones ? (algoritmo de Viterbi)
- Dada una secuencia de observaciones , ¿cómo podemos estimar los parámetros del modelo para maximizar . En este caso el objetivo es encontrar el modelo que mejor explica la secuencia observada (algoritmo de Baum-Welch).
MODELOS OCULTOS DE MARKOV
Consideraciones Importantes:
Se cumple la probabilidad de Markov:
- Si la probabilidad de cada estado depende únicamente del estado anterior (propiedad de Markov)

- Axioma de probabilidad:

Usos de los Modelos Ocultos de Markov:Existen tres problemas canónicos asociados con HMM:Dados los parámetros del modelo, compútese la probabilidad de una secuencia de salida en particular. Este problema se resuelve con el algoritmo de avance-retroceso.Dados los parámetros del modelo, encuéntrese la secuencia más probable de estados ocultos que puedan haber generado una secuencia de salida dada. Este problema se resuelve con el algoritmo de Viterbi.Dada una secuencia de salida o un conjunto de tales secuencias, encuéntrese el conjunto de estados de transición y probabilidades de salida más probables. En otras palabras, entrénense a los parámetros del HMM dada una secuencia de datos. Este problema se resuelve con el algoritmo de Baum-Welch.Algoritmo de Forward – Backward:Uno de los problemas básicos de los Modelos Ocultos de Márkov es el cálculo de la probabilidad de una secuencia de observables dado un modelo. El objetivo es por tanto calcular eficientemente la Probabilidad de una secuencia de estados. Se divide en 2 pasos:- Forward: Se busca cada αt de forma iterativa
- Backward: Se busca cada βt de forma iterativaLa probabilidad de la secuencia es proporcional a αt βt
Algoritmo de Viterbi:El algoritmo de Viterbi es un algoritmo de programación dinámica que permite hallar la secuencia mas probable de estados ocultos que produce una secuencia observada de sucesos, especialmente en el contexto de fuentes de información de Markov y Modelos ocultos de Markov.Algoritmo de Baum – Welch:Uno de los problemas relacionados con los Modelos Ocultos de Márkov (MOM) es el de encontrar un modelo que maximice la probabilidad de una secuencia, es decir, determinar el modelo que mejor explica tal secuencia. El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables.cia de observaciones.Caso de uso: Viterbi



























![{\displaystyle \alpha _{t+1}(j)={\biggl [}\displaystyle \sum _{i=1}^{N}{\alpha _{t}(i)a_{ij}}{\biggr ]}b_{j}(o_{t+1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3226e1dc082e9c82be9f84a2e92b2f2ef5e8751a)




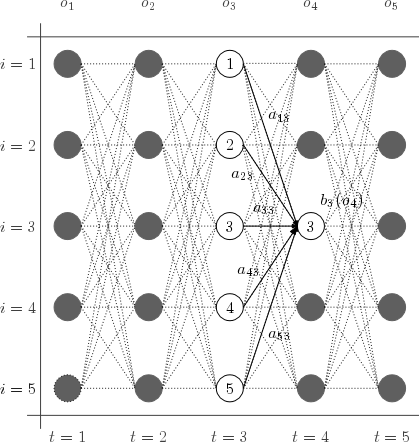
![{\displaystyle \alpha _{4}(3)={\biggl [}\displaystyle \sum _{i=1}^{5}{\alpha _{3}(i)a_{i3}}{\biggr ]}b_{3}(o_{4})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71b549caf1e5df14e80d713015e781ee2841ff92)















No hay comentarios:
Publicar un comentario