Un alineamiento múltiple de secuencias (MSA, por sus siglas en inglés) es un alineamiento de tres o más secuencias biológicas, generalmente proteínas, ADN o ARN. En general, se asume que el conjunto de secuencias de consulta que se ingresa como entrada (conjunto problema) tienen una relación evolutiva por la cual comparten un linaje y descienden de un ancestro común. Del MSA resultante, se puede inferir la homología, y puede llevarse a cabo el análisis filogenético para evaluar los orígenes evolutivos compartidos por las secuencias. Las representaciones visuales del alineamiento ilustran mutaciones tales como mutaciones puntuales (un solo cambio de aminoácidos o nucleótidos) que aparecen como diferentes caracteres en una sola columna del alineamiento, y la inserción o supresión de mutaciones (o indels) que aparecen como huecos en una o varias de las secuencias en la alineación. El alineamiento múltiple de secuencias a menudo se utiliza para evaluar la conservación de los dominios proteicos, las estructuras terciarias y secundarias, e incluso aminoácidos o nucleótidos individuales.
Los alineamientos múltiples de secuencias también se refieren al proceso de alinearlas como un conjunto de secuencias. Como puede ser difícil alinear a mano tres o más secuencias de longitud biológicamente relevante, y casi siempre consume mucho tiempo, se utilizan algoritmoscomputacionales para producir y analizar los alineamientos. Los MSA requieren metodologías más sofisticadas que los alineamiento de pares porque son computacionalmente más complejos de producir. La mayor parte de los programas de alineamiento múltiple de secuencias usan métodos heurísticos en lugar de optimización global, porque identificar el alineamiento óptimo entre más de unas pocas secuencias de longitud moderada es prohibitivamente costoso computacionalmente.
Programación dinámica y complejidad computacional[editar]
El método más directo para producir alineamientos múltiples de secuencias utiliza la técnica de programación dinámica para identificar la solución de alineamiento globalmente óptima. Para las proteínas, este método supone normalmente dos conjuntos de parámetros: una penalización por gap (o hueco) y una matriz de sustitución que asigna puntuaciones o probabilidades al alineamiento de cada posible par de aminoácidos basadas en la similitud de las propiedades químicas de los mismos o en la probabilidad evolutiva de la mutación. Para secuencias de nucleótidos puede usarse una matriz de sustitución, pero dado que sólo hay cuatro caracteres estándar posibles por secuencia, y que los nucleótidos individuales no difieren mucho en su probabilidad de sustitución, los parámetros para secuencias de ADN y ARN consisten, normalmente, en una penalización por gap, una puntuación positiva para coincidencias de caracteres, y una puntuación negativa para desigualdades.
Para n secuencias individuales, el método requiere construir el equivalente n-dimensional de la matriz formada en el alineamiento estándar de pares de secuencias de la programación dinámica. De esta forma, el espacio de búsqueda se incrementa exponencialmente conforme se incrementa n, dependiendo también fuertemente de la longitud de la secuencia. Encontrar de esta forma el óptimo global para n secuencias ha mostrado ser un problema NP-completo.12 Los métodos para reducir el espacio de búsqueda efectuando inicialmente alineamientos de pares mediante programación dinámica sobre cada par de secuencias en el conjunto problema, y buscando sólo el espacio solución cerca de estos resultados (encontrando de forma efectiva la intersección entre trayectorias locales en los alrededores inmediatos de cada solución óptima de alineamiento por pares) representan la técnica de programación dinámica más eficiente. El método denominado "suma de pares" se ha implementado en el software MSA, pero no es todavía práctico para la mayoría de aplicaciones de alineamiento múltiple de secuencias que requieren el alineamiento simultáneo de docenas (y aún de varios centenares) de secuencias. Los métodos de programación dinámica sólo se usan ahora cuando se necesita un alineamiento de muy alta calidad entre un pequeño número de secuencias, así como benchmark estándar en la evaluación de nuevas o mejoradas técnicas heurísticas.
Construcción progresiva del alineamiento[editar]
Un método para realizar una búsqueda heurística del alineamiento es la técnica progresiva (también conocido como método jerárquico o de árbol) que construye un alineamiento múltiple final realizando primero una serie de alineamientos de pares sobre secuencias sucesivamente menos emparentadas. Tales métodos comienzan alineando en primer lugar las dos secuencias más cercanamente relacionadas, para seguir alineando sucesivamente la siguiente secuencia del conjunto problema más emparentada con el alineamiento producido en el paso previo. El par inicial "más relacionado", o emparentado, se determina mediante un método eficiente de categorización (o clustering) tal como el neighbour-joining, basado en una simple búsqueda heurística del conjunto problema con una herramienta como FASTA. Las técnicas progresivas, por tanto, construyen automáticamente tanto un árbol filogenético como un alineamiento.
Una limitación importante de los métodos progresivos es su fuerte dependencia de la asignación inicial del parentesco entre las secuencias, así como de la calidad del alineamiento inicial. De este modo, los métodos son sensibles también a la distribución de las secuencias en el conjunto problema: el rendimiento mejora cuando la cuantificación de la estructura del parentesco entre las secuencias problema compone un gradiente relativamente suave en lugar de encontrarse en categorías distantes. También se degrada significativamente el rendimiento cuando todas las secuencias del conjunto están bastante lejanamente relacionadas, ya que entonces son más probables las imprecisiones en el alineamiento inicial. Los métodos progresivos más modernos modifican su función de puntuación con una función de ponderación secundaria que asigna individualmente factores de escala a miembros del conjunto problema de forma no lineal, basada en su distancia filogenética a sus vecinos más próximos. Una elección juiciosa de los pesos puede ayudar en la evaluación de las relaciones y mitigar los efectos de alineamientos iniciales relativamente pobres en instantes tempranos de la progresión.
Los métodos de alineamiento progresivo son lo bastante eficientes como para implementarlos a gran escala para muchas secuencias, y se ejecutan a menudo en servidores web públicamente accesibles, por lo que los usuarios no necesitan instalar localmente las aplicaciones de interés. Un método de alineamiento progresivo muy popular es la familia Clustal,3 especialmente la variante ponderada ClustalW,4 cuyo acceso se proporciona en un buen número de portales web, incluyendo GenomeNet, EBI y EMBNet. Diferentes portales o implementaciones pueden variar la interfaz con el usuario y hacer accesibles a éste diferentes parámetros. Se usa Clustal extensivamente en la construcción de árboles filogenéticos y como input para la predicción de la estructura de proteínas mediante modelado por homología.
Otro método común de alineamiento progresivo denominado T-Coffee5 es más lento que Clustal y sus derivados, pero generalmente produce alineamientos más precisos para conjuntos de secuencias lejanamente emparentadas. T-Coffee calcula alineamientos de pares combinando el alineamiento directo del par con alineamientos indirectos que alinean cada secuencia del par con una tercera. Usa la salida de Clustal así como otro programa de alineamiento local, LALIGN, que encuentra regiones múltiples de alineamiento local entre dos secuencias. Los alineamientos y el árbol filogenético resultantes se usan como guía para producir nuevos y más precisos factores de ponderación.
Puesto que los métodos progresivos son heurísticos y, por lo tanto, no garantizan la convergencia a un óptimo global, la calidad del alineamiento puede ser difícil de evaluar, y su verdadera significación biológica puede ser oscura. Un muy reciente método semiprogresivo que mejora la calidad del alineamiento y que no utiliza una heurística "con pérdidas" a la vez que se ejecuta en tiempo polinómico6 se ha implementado en el programa PSAlign.
Métodos iterativos[editar]
Un conjunto de métodos para producir alineamientos múltiples de secuencias que reducen los errores inherentes en los métodos progresivos son los clasificados como “iterativos”, ya que trabajan de forma similar a los métodos progresivos, pero realinean repetidamente las secuencias iniciales además de añadir nuevas secuencias al MSA en crecimiento. Una razón por la que los métodos progresivos son tan fuertemente dependientes de la alta calidad del alineamiento inicial es el hecho de que estos alineamientos se incorporan siempre al resultado final; esto es, una vez que una secuencia ha sido alineada dentro del MSA, su alineamiento no vuelve a ser considerado. Este enfoque mejora la eficiencia a costa de la precisión. En contraste, los métodos iterativos pueden volver a alineamientos de pares previamente calculados (o sub-MSAs) incorporando subconjuntos de la secuencia problema como un medio de optimización de una función objetivo general, tal como encontrar una puntuación de alineamiento de alta calidad.
Se ha implementado una variedad de métodos de iteración sutilmente diferentes, que han sido dispuestos en diferentes paquetes de software. Existen revisiones y comparaciones útiles, pero evitan, generalmente, elegir la "mejor" técnica.7
El paquete PRRN/PRRP utiliza un algoritmo hill climbing (ascenso a colina, en alguna literatura) para optimizar su puntuación de alineamiento del MSA8 y corregir iterativamente tanto las ponderaciones del alineamiento como las regiones localmente divergentes (con huecos) del alineamiento múltiple de secuencias en crecimiento.9 PRRP actúa mejor cuando refina un alineamiento previamente construido por un método más rápido.9
Otro programa iterativo, DIALIGN, toma una inusual aproximación al concentrarse estrechamente sobre alineamientos locales entre subsegmentos o secuencias motivo sin introducir una penalización por hueco.10 Se consigue el alineamiento de motivos individuales con una representación matricial similar a una gráfica de matriz de puntos en un alineamientos de pares. Un método alternativo que utiliza alineamientos locales rápidos como puntos de referencia o "semillas" para un procedimiento más lento de alineamiento global se implementa en la suite CHAOS/DIALIGN.11
Un tercer método popular basado en la iteración, llamado MUSCLE (de multiple sequence alignment by log-expectation, o alineamiento múltiple de secuencias por log-esperanza; este último término corresponde a una función de puntuación no común basada en la esperanza matemática, y resultado de modificar la función log-average o log-promedio), mejora en relación a los métodos progresivos con una medida más precisa de la distancia para valorar el parentesco de dos secuencias.12 La medición de la distancia se actualiza entre las etapas de la iteración (sin embargo, en su forma original, MUSCLE contenía sólo dos o tres iteraciones, dependiendo de si se activaba o no el refinamiento).
Modelos de Márkov ocultos[editar]
Los modelos de Márkov ocultos (o HMM, del inglés Hidden Márkov Models) son modelos probabilísticos que asignan probabilidades a todas las posibles combinaciones de huecos, coincidencias y diferencias para determinar el más probable alineamiento múltiple de secuencias o conjunto de posibles MSA. Los HMM pueden producir una salida única con la mayor puntuación, pero también pueden generar una familia de alineamientos posibles que puedan ser evaluados en su significación biológica. Dado que los modelos ocultos de Márkov son probabilísticos, no producen la misma solución cada vez que se ejecutan sobre el mismo conjunto de datos; de esta forma, no pueden garantizar converger al alineamiento óptimo. Los HMM pueden producir alineamientos tanto locales como globales. Aunque los métodos basados en estos modelos han sido desarrollados recientemente, ofrecen mejoras significativas en la velocidad computacional, especialmente para secuencias que contienen regiones solapadas.9
Los métodos típicos basados en HMM trabajan representando un MSA bajo la forma de grafo dirigido acíclico, conocido como un grafo de orden parcial, y que consiste en una serie de nodos representando posibles entradas en las columnas de un alineamiento múltiple de secuencias. En esta representación, una columna que esté absolutamente conservada (esto es, que todas las secuencias en el MSA compartan un carácter determinado en esa posición en particular) se codifica como un único nodo con tantas conexiones salientes como posibles caracteres haya en la siguiente columna del alineamiento. En los términos de un típico modelo oculto de Márkov, los estados observados son las columnas individuales del alineamiento, y los estados "ocultos" representan la supuesta secuencia ancestral desde la cual las secuencias del conjunto problema se presume han descendido. Una variante de búsqueda eficiente del método de programación dinámica, conocida como algoritmo de Viterbi, se usa generalmente para alinear sucesivamente el MSA en crecimiento con la siguiente secuencia del conjunto problema para generar un nuevo MSA.13 Esto es diferente de los métodos de alineamiento progresivo puesto que el alineamiento de las secuencias previas se actualiza en cada adición de una nueva secuencia. Sin embargo, como en los métodos progresivos, esta técnica puede verse influenciada por el orden en el cual las secuencias del conjunto problema son integradas al alineamiento, especialmente cuando las secuencias están lejanamente relacionadas.9
Pueden encontrarse bastantes programas de software en los cuales se han implementado variantes de los métodos basados en HMM, y que se caracterizan por su escalabilidad y eficiencia, aunque el uso correcto de un método HMM es más complejo que el de los métodos progresivos más comunes. El más sencillo es POA(Partial-Order Alignment, alineamiento de orden parcial).14 Un método similar, pero más general, se implementa en el paquete SAM (Sequence Alignment and Modeling System, sistema de alineamiento y modelado de secuencia).15 SAM se ha usado como una fuente de alineamientos para predicción de estructura de proteínas al participar en el experimento de predicción de estructura CASP (de Critical Assessment of Techniques for Protein Structure Prediction, valoración crítica de técnicas para predicción de la estructura de proteínas), y para desarrollar una base de datos de proteínas predichas en la especie de levadura S. cerevisiae. Los métodos HMM también pueden usarse para búsquedas en bases de datos con HMMer.16
Algoritmos genéticos y simulated annealing[editar]
En el intento de producir MSA de calidad de forma más eficiente también se han usado algunas técnicas de optimización estándar en ciencias de la computación inspiradas por procesos físicos (pero que no los reproducen directamente). Una de tales técnicas, los algoritmos genéticos, se han utilizado en la producción de MSA intentando simular, en líneas generales, el hipotético proceso evolutivo que da lugar a la divergencia en el conjunto problema. Este método trabaja rompiendo en fragmentos una serie de posibles MSA y reordenando repetidamente estos fragmentos con la introducción de huecos en diferentes posiciones. Una función objetivogeneral se optimiza durante la simulación, normalmente una función de maximización "suma de pares" introducida en los métodos de MSA de programación dinámica. Se ha implementado una técnica para secuencias de proteínas en el programa de software SAGA (Sequence Alignment by Genetic Algorithm, alineamiento de secuencias por algoritmo genético),17 denominándose RAGA su equivalente para ARN.18
Mediante la técnica de simulated annealing (tienen relativamente poco éxito en la literatura en castellano traducciones como "temple" o "recocido" simulado), un alineamiento múltiple de secuencias existente, producido por otro método, se refina por una serie de reordenamientos diseñados para encontrar regiones más óptimas del espacio de alineamiento que la ya ocupada por el MSA previo. Al igual que en el método de algoritmos genéticos, en simulated annealing se maximiza una función objetivo como la suma de pares. Este método utiliza un "factor de temperatura" metafórico que determina el ritmo al cual los reordenamientos avanzan, así como la probabilidad de cada uno de ellos. Un uso típico alterna periodos de altos ritmos de reorganización y relativamente baja probabilidad (para explorar regiones más distantes del espacio de alineamiento), con periodos de bajos ritmos y más altas probabilidades para explorar a fondo mínimos locales cerca de las regiones recientemente “colonizadas”. Este enfoque ha sido implementado en el programa MSASA (Multiple Sequence Alignment by Simulated Annealing, alineamiento múltiple de secuencias por simulated annealing).19
Descubrimiento de motivos[editar]
El descubrimiento de motivos, también conocido como análisis de perfiles, es un método de localización de motivos de secuencia en MSA globales, y que supone tanto un medio para producir mejores alineamientos múltiples de secuencias como para producir una matriz de puntuación para ser usada en la búsqueda de motivos similares en otras secuencias. Se han desarrollado varios métodos para aislar los motivos, pero todos están basados en la identificación de patrones cortos altamente conservados dentro de un alineamiento mayor, y en la construcción de una matriz, similar a una de sustitución, que refleje la composición de aminoácidos o nucleótidos de cada posición en el supuesto motivo. Los alineamientos se pueden refinar entonces usando estas matrices. En el análisis estándar de perfiles, la matriz incluye entradas para cada posible carácter, así como entradas para huecos.9 Alternativamente, los algoritmos estadísticos de descubrimiento de patrones pueden identificar motivos como precursores de MSA, en lugar de como derivados. En muchos casos, cuando el conjunto de secuencias problema contiene sólo un pequeño número de secuencias, o contiene sólo secuencias altamente relacionadas, se añaden seudocontadores para normalizar la distribución reflejada en la matriz de puntuación. Esto corrige, en particular, entradas en la matriz con probabilidad cero mediante valores pequeños, pero no nulos.
El análisis de bloques es un método de descubrimiento de motivos que los restringe a regiones sin huecos en el alineamiento. Los bloques se pueden generar desde un MSA o pueden ser extraídos de secuencias sin alinear usando un conjunto precalculado de motivos previamente generado desde familias conocidas de genes.20 La puntuación de los bloques depende generalmente del espaciado de los caracteres con altas frecuencias, en lugar de recaer sobre el cálculo de una matriz de sustitución explícita. El servidor BLOCKS proporciona un método interactivo para localizar tales motivos en secuencias sin alinear.
Se han implementado comparadores de patrones utilizando tanto el algoritmo expectación-maximización como el muestreo de Gibbs. Una de las más comunes herramientas de descubrimiento de motivos, denominada MEME, utiliza expectación-maximización y modelos ocultos de Márkov para generar motivos que luego se usan como herramientas de búsqueda por su compañero MAST en la suite combinada MEME/MAST.
ALINANEAMIENTOS MULTIPLES
Introducción
Un alineamiento múltiple de secuencias es un alineamiento de más de dos secuencias. Estas secuencias, como en el caso de los alieamientos por parejas pueden ser ADN, ARN o proteína.

Las aplicaciones más habituales de los alineamientos múltiples son:
- la reconstrucción filogenética,
- el análisis estructural de proteínas,
- la búsqueda de dominios conservados y
- la búsqueda de regiones conservadas en promotores.
En todos los casos los algoritmos de alineamiento múltiple asumen que las secuencias que estamos alineando descienden de un antepasado común y lo que intentamos hacer es alinear las posiciones homólogas.

Un par de revisiones recientes sobre los métodos de construcción de alineamientos múltiple: A Comprehensive Benchmark Study of Multiple Sequence Alignment Methods: Current Challenges and Future Perspectives y Evaluating the Accuracy and Efficiency of Multiple Sequence Alignment Methods.
Métodos similares que no son alineamientos múltiples
Existen algunos algoritmos relacionados que no suelen ser considerados métodos de alineamientos multiples a pesar de alinear varias secuencias. El primero es el ensamblaje de varias lecturas provenientes de un proyecto de secuenciación. En este caso no estamos alineando secuencias homólogas sino fragmentos de una secuencia desconocida mayor. Este problema viola una asunción que suelen hacer los algoritmos de alineamiento múltiple. Las secuencias no cubren la misma región. Esto haría que la mayor parte de los algoritmos de alinemiento múltiple fallasen al darnos la solución o, en el mejor de los casos, que sí nos den una buena solución, pero que resulten extraordinariamente ineficientes. Los algoritmos de alineamiento múltiple están pensados para alinear secuencias que cubren la misma región, por ejmeplo una proteína, y para alinear secuencias relativamente diferenciadas. Los algoritmos de ensamblaje son capaces de resolver el problema de un modo mucho más eficiente puesto que asumen que las lecturas que provienen de una secuencia problema única y que, por lo tanto, son prácticamente idénticas.
El segundo caso de aparente alieamientos múltiple que no lo es es el de la resecuenciación y la comparación con una secuencia de referencia. Si obtenemos lecturas de uno o varios individuos mediante cualquier técnica de secuenciación y queremos alinear las lecturas contra la secuencia de referencia (por ejemplo un genoma) no debemos utilizar un método de alineamiento múltiple o un método de ensamblaje. Estos métodos serían muy ineficientes. La solución sería utilizar un método de alineamiento secuencias por parejas optimizado para secuencias muy similares con una de ellas muy larga y la otra muy corta. Estos algoritmos son aplicados para alinear cada una de las lecturas contra la secuencia de referencia y son capaces de alinear millones de secuencias por hora mientras que cualquier algoritmo habitual de alineamiento múltiple fallaría con la primera secuencia ya que no están preparados para alinear secuencias tan largas como un genoma.
Otra aplicación que sí está realacionada con los métodos de alineamiento múltiple es la búsqueda de bloques o dominios consevados. En este caso el objetivo no es crear un alineamiento amplio que cubra la mayor parte de la secuencias sino localizar solamente las regiones conservadas. Estos métodos se basan en localizar pequeños motivos conservados y en crear matrices que reflejen la composición de cada una de las posiciones de estos motivos a lo largo de todas las secuencias analizadas. Existen numerosos algoritmos de búsquedas de motivos como: Blocks o meme.
Algoritmos de alineamiento múltiple
El problema del alinemiento múltiple es computacionalmente más complejo que el del alineamiento por parejas de secuencias. En este caso no es posible aplicar un algoritmo equivalente al de Smith Waterman para parejas de secuencias que nos garantice un resultado óptimo dado un esquema de puntuación para cambios y gaps. Este algoritmo requeriría construir y explorar una matriz de n-dimensiones (una por cada secuencia) lo que requeriría un tiempo que crecería exponencialmente con el número y la longitud de las secuencias. Dada la imposibilidad práctica de dicho método ningún programa usual lo implementa y todos recurren a algoritmos que utilizan distintos métodos heurísticos para simplificar el problema. Esto implica que cada método asumirá ciertas características en las secuencias y que renunciará a alinear correctamente ciertos tipos de secuencias.
Los algoritmos de alineamiento múltiple están pensados para alinear secuencias bastante diferentes entre sí. A pesar de ello a medida que estas diferencias aumenten a los algoritmos les será más difícil dar con el alineamiento correcto, es decir, el correspondiente a las relaciones de homología reales.
Una de las asunciones que suelen hacer estos algoritmos para poder resolver el problema es que las secuencias a alinear cubren la misma región y que no hay muchas inserciones y deleciones grandes. Estas restricciones hacen que estos algoritmos estén especialmente indicados para algunos problemas, pero no para otros y que no todas las secuencias se alineen igual de bien. Por ejemplo, si estamos alineando proteínas homólogas provenientes de especies muy separadas filogenéticamente nos será más fácil alinear las regiones más conservadas y puede que tengamos problemas con las regiones más variables. En el caso de las secuencias de ADN correspondientes a genes suele ser más fácil alinear las regiones codificantes que las no codificantes debido al mayor grado de conservación de las regiones codificantes. Estos algoritmos tenderán a no comportarse bien con secuencias parcialmente solapantes, como las lecturas proveninentes de un proyecto de secuenciación.
Algoritmos de construcción progresiva
Los métodos más utilzados suelen utilizar una heurística de alineación progresiva. Estos algoritmos son muy utilizados porque son bastante rápidos y permiten, por lo tanto, alinear miles de secuencias en tiempos cortos. Antes de comenzar a realizar el alineamiento debemos establecer el esquema de puntuación de los posibles alineamientos. Es decir, cuales son las penalizaciones por introduccir o amplicar un gap y por las diferencias entre residuos. El objetivo de cualquier algoritmo debería ser obtener un alineamiento con la mínima puntuación posible.
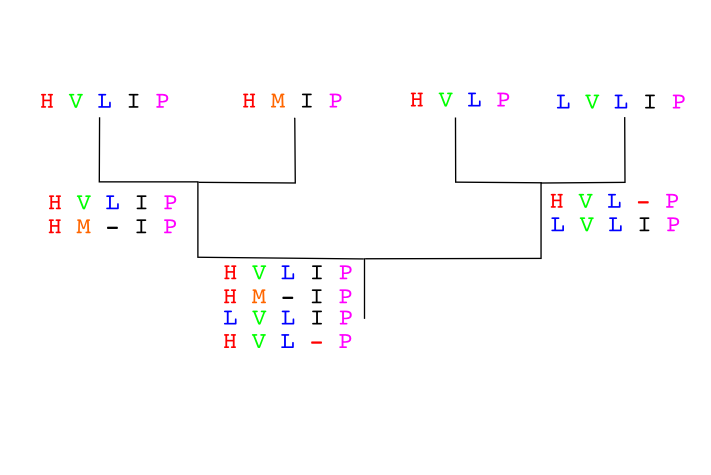
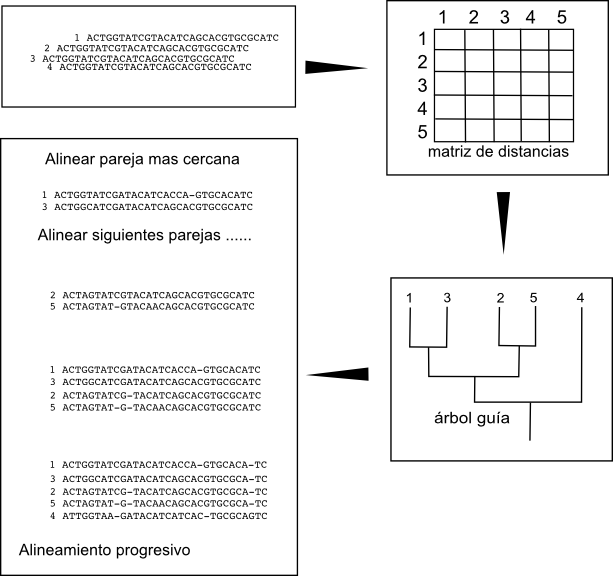
Los algoritmos de construcción progresiva empiezan por alienar las parejas de secuencias más similares y después, progresivamente, van añadiendo al alineamiento secuencias cada vez más diferentes. Para hacerlo comienzan por crear un árbol de secuencias basado en las similitudes obtenidas a partir de los alineamientos por parejas. Este árbol es denominado árbol guía. Una vez creado este árbol guía (normalmente por UPGMA o Neighbor joining) se buscan las parejas más similares y a partir de ellas se comienza a crear el alineamiento múltiple añadiendo secuencialmente las secuencias por el orden dictado por el árbol guía.
Otro ejemplo:
Distancias:
IMPRESIONANTE X IMPRESO 7/13
IMPRESIONANTE X INCUESTIONABLE 10/14
INCUESTIONABLE X IMPRESO 4/14
El primer alineamiento seria: Incuestionableximpresioante.
IMPRES-IONABLE
INCUESTIANABLE
Posteriormente uniría Impreso
IMPRES-IONANTE
INCUESTIONABLE
IMPRES--O-----
No tenemos garantía de que el alineamiento múltiple obtenido sea el alineamiento óptimo, es decir, que sea el que minimice la puntuación dado el esquema de puntuación que debemos haber establecido a priori. La principal debilidad de estos algoritmos de construcción progresiva es que los errores introduccidos en cualquiera de las etapas de alineamiento no son corregidos en etapas posteriores sino que son propagados hasta el resultado final. Por ejemplo, si en el primer alineamiento de la pareja de secuencias más cercanas introducimos un gap en una posición, este gap se propagará añadiéndose a todas las secuencias que lo requieran en las etapas posteriores. Si el gap estaba bien puesto esto no es un problema, pero si fuese un error éste error no será corregido. Estos métodos se comportan especialmente mal cuando las secuencias son muy distantes.
Los algoritmos de la familia del Clustal han sido históricamente los más utilizados, especialmente ClustalW. La versión actual del ClustalW es el ClustalW2. El clustalW no se encuentra actualmente entre los más recomendados puesto que hay otros algoritmos que presentan un mejor comportamiento, por ejemplo el Clustal Omega para proteínas o el MAFFT. El MAFFT fue uno de los programas con una mejor puntuación en una comparación de programas de alinemiento múltiple y, además, fue muy rápido.
Otro algoritmo de construcción progresiva es el T-Coffee. Es más lento que el Clustal porque calcula los alineamientos por parejas teniendo en cuenta otras secuencias cercanas del árbol guía.
https://bioinf.comav.upv.es/courses/intro_bioinf/multiple.html


No hay comentarios:
Publicar un comentario