QUÍMICA FÍSICA

Armónicos cúbicos

En campos como la química computacional y de estado sólido y de la materia condensada física los llamados orbitales atómicos , o spin-orbitales , tal como aparecen en los libros de texto ^{[1] [2] [3]} en la física cuántica, a menudo se sustituye parcialmente por armónicos cúbicos por un número de razones.

Introducción [ editar ]

los $${\ displaystyle l (l + 1)} Orbitales atómicos similares al hidrógeno con número cuántico principal$${\ displaystyle n} y el momento angular número cuántico $${\ displaystyle l} a menudo se expresan como

$${\ displaystyle \ psi _ {nlm} (\ mathbf {r}) = R_ {nl} (r) Y_ {l} ^ {m} (\ theta, \ varphi)}

en el que la $${\ displaystyle R_ {nl} (r)} es la parte radial de la función de onda y $${\ displaystyle Y_ {l} ^ {m} (\ theta, \ varphi)}Es la parte dependiente angular. los$${\ displaystyle Y_ {l} ^ {m} (\ theta, \ varphi)}Son los armónicos esféricos , que son soluciones del operador del momento angular . Los armónicos esféricos son representaciones de funciones del grupo de rotación completa SO (3) ^[4] con simetría rotacional. En muchos campos de la física y la química, estos armónicos esféricos se reemplazan por armónicos cúbicosporque la simetría rotacional del átomo y su entorno están distorsionados o porque los armónicos cúbicos ofrecen beneficios computacionales .

Simetría y sistema de coordenadas [ editar ]

En muchos casos, especialmente en la química y de estado sólido y de la materia condensada física , el sistema bajo investigación no tiene simetría rotacional. A menudo tiene algún tipo de simetría inferior , con una representación de grupo de puntos especial , o no tiene simetría espacial en absoluto . Los sistemas biológicos y bioquímicos , como los aminoácidos y las enzimas, a menudo pertenecen a grupos de puntos de baja simetría molecular . Los cristales sólidos de los elementos a menudo pertenecen a los grupos espaciales.y grupos de puntos con alta simetría. (Las representaciones de armónicos cúbicos a menudo se enumeran y hacen referencia en las tablas de grupos de puntos ). El sistema tiene al menos una orientación fija en el espacio euclidiano tridimensional . Por lo tanto, el sistema de coordenadas que se usa en tales casos es más a menudo un sistema de coordenadas cartesiano en lugar de un sistema de coordenadas esférico . En un sistema de coordenadas cartesiano, los orbitales atómicos se expresan a menudo como

$${\ displaystyle \ psi _ {nlc} (\ mathbf {r}) = R_ {nl} (r) X_ {lc} (\ mathbf {r})}

con los armónicos cúbicos , ^{[5] [6] [7]} $${\ displaystyle X_ {lc} (\ mathbf {r})}, como base establecida . Los cálculos de LCAO y MO en química computacional o cálculos de enlace estricto en física de estado sólido utilizan armónicos cúbicos como una base orbital atómica. Los índices lc denotan algún tipo de representación cartesiana.

Transformaciones de base [ editar ]

Para las representaciones de los armónicos esféricos, se elige un sistema de coordenadas esféricas con un eje principal en la dirección z . Para los armónicos cúbicos, este eje es también la opción más conveniente. Para estados de mayor cantidad de momento angular.$${\ displaystyle l} y una dimensión superior de $${\ displaystyle l (l + 1)}el número de rotaciones posibles o transformaciones de base en el espacio de Hilbert crece, al igual que el número de posibles representaciones ortogonales que se pueden construir sobre la base de$${\ displaystyle l (l + 1)}Conjunto de bases armónicas esféricas tridimensionales. Hay más libertad para elegir una representación que se ajuste a la simetría del grupo de puntos del problema. Las representaciones cúbicas que se enumeran en la tabla son el resultado de las transformaciones, que son rotaciones de 45 ° 2D y una rotación de 90 ° al eje real si es necesario, como

$${\ displaystyle X_ {lc} (\ mathbf {r}) = Y_ {l} ^ {0}}

$${\ displaystyle X_ {lc '} (\ mathbf {r}) = {\ frac {1} {i ^ {n_ {c'}} {\ sqrt {2}}}} \ left (Y_ {l} ^ { m} -Y_ {l} ^ {- m} \ derecha)}

$${\ displaystyle X_ {lc ''} (\ mathbf {r}) = {\ frac {1} {i ^ {n_ {c ''}} {\ sqrt {2}}}} \ left (Y_ {l} ^ {m} + Y_ {l} ^ {- m} \ derecha)}

Un número sustancial de los armónicos esféricos se enumeran en la Tabla de armónicos esféricos .

Beneficios computacionales [ editar ]

Ferricianuro de iones, que se utiliza para hacer 'Turnbull azul' con un centro de octahedrically rodeada Fe ³⁺ion.

En primer lugar, los armónicos cúbicos son funciones reales , mientras que los armónicos esféricos son funciones complejas . Los números complejos son bidimensionales con una parte real y una parte imaginaria. Los números complejos ofrecen herramientas muy atractivas y eficaces para abordar problemas matemáticos de manera analítica, pero no son muy efectivos cuando se usan para cálculos numéricos. Al omitir la parte imaginaria, se ahorra la mitad del esfuerzo de cálculo en sumas, un factor de cuatro en las multiplicaciones y, a menudo, factores de ocho o incluso más cuando se trata de cálculos con matrices.

Los armónicos cúbicos a menudo se ajustan a la simetría del potencial o entorno de un átomo. Un entorno común de átomos en sólidos y complejos químicos es un círculo octaédrico con una simetría de grupo de puntos cúbicos octaédricos . Las representaciones de los armónicos cúbicos a menudo tienen una alta simetría y multiplicidad, por lo que las operaciones como las integraciones se pueden reducir a una parte limitada o irreductible del dominio de la función que se debe evaluar. Un problema con el 48 veces octaédrico O _h simetría se puede calcular mucho más rápido si se limita un cálculo, como una integración, a la parte irreductible del dominio de la función.

Tabla de armónicos cúbicos [ editar ]

Los orbitales s [ editar ]

Los orbitales s solo tienen una parte radial.

$${\ displaystyle \ psi _ {n00} (\ mathbf {r}) = R_ {n0} (r) Y_ {0} ^ {0}}

$${\ displaystyle s = X_ {00} = Y_ {0} ^ {0} = {\ frac {1} {\ sqrt {4 \ pi}}}}

	n = 1	2	3	4	5	6	7
Rn0

Los orbitales p [ editar ]

Los tres orbitales p son orbitales atómicos con un número cuántico de momento angular ℓ = 1 . La expresión armónica cúbica de los p-orbitales.

$${\ displaystyle p_ {z} = N_ {1} ^ {c} {\ frac {z} {r}} = Y_ {1} ^ {0}}

$${\ displaystyle p_ {x} = N_ {1} ^ {c} {\ frac {x} {r}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ {1} ^ { -1} -Y_ {1} ^ {1} \ derecha)}

$${\ displaystyle p_ {y} = N_ {1} ^ {c} {\ frac {y} {r}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ {1} ^ { -1} + Y_ {1} ^ {1} \ derecha)}

con

$${\ displaystyle N_ {1} ^ {c} = \ left ({\ frac {3} {4 \ pi}} \ right) ^ {1/2}}

p z	p x	p y

Los orbitales d [ editar ]

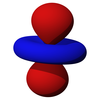
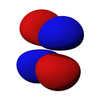
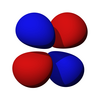
Los cinco orbitales d son orbitales atómicos con un número cuántico de momento angular ℓ = 2 . La parte angular de los orbitales d a menudo se expresa como

$${\ displaystyle \ psi _ {n2c} (\ mathbf {r}) = R_ {n2} (r) X_ {2c} (\ mathbf {r})}

La parte angular de los orbitales d son los armónicos cúbicos. $${\ displaystyle X_ {2c} (\ mathbf {r})}

$${\ displaystyle d_ {z ^ {2}} = N_ {2} ^ {c} {\ frac {3z ^ {2} -r ^ {2}} {2r ^ {2} {\ sqrt {3}}} } = Y_ {2} ^ {0}}

$${\ displaystyle d_ {xz} = N_ {2} ^ {c} {\ frac {xz} {r ^ {2}}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ { 2} ^ {- 1} -Y_ {2} ^ {1} \ derecha)}

$${\ displaystyle d_ {yz} = N_ {2} ^ {c} {\ frac {yz} {r ^ {2}}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ { 2} ^ {- 1} + Y_ {2} ^ {1} \ derecha)}

$${\ displaystyle d_ {xy} = N_ {2} ^ {c} {\ frac {xy} {r ^ {2}}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ { 2} ^ {- 2} -Y_ {2} ^ {2} \ derecha)}

$${\ displaystyle d_ {x ^ {2} -y ^ {2}} = N_ {2} ^ {c} {\ frac {x ^ {2} -y ^ {2}} {2r ^ {2}}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ {2} ^ {- 2} + Y_ {2} ^ {2} \ right)}

con

$${\ displaystyle N_ {2} ^ {c} = \ left ({\ frac {15} {4 \ pi}} \ right) ^ {1/2}}

d z 2	d xz	d yz	d xy	d x 2 -y 2

Los orbitales f [ editar ]

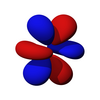
Los siete orbitales f son orbitales atómicos con un número cuántico de momento angular ℓ = 3 . a menudo expresado como

$${\ displaystyle \ psi _ {n3c} (\ mathbf {r}) = R_ {n3} (r) X_ {3c} (\ mathbf {r})}

La parte angular de los orbitales f son los armónicos cúbicos. $${\ displaystyle X_ {3c} (\ mathbf {r})}. En muchos casos, se eligen diferentes combinaciones lineales de armónicos esféricos para construir un conjunto de bases orbital cúbicas.

$${\ displaystyle f_ {z ^ {3}} = N_ {3} ^ {c} {\ frac {z (2z ^ {2} -3x ^ {2} -3y ^ {2})} {2r ^ {3 } {\ sqrt {15}}}} = Y_ {3} ^ {0}}

$${\ displaystyle f_ {xz ^ {2}} = N_ {3} ^ {c} {\ frac {x (4z ^ {2} -x ^ {2} -y ^ {2})} {2r ^ {3 } {\ sqrt {10}}}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ {3} ^ {- 1} -Y_ {3} ^ {1} \ right)}

$${\ displaystyle f_ {yz ^ {2}} = N_ {3} ^ {c} {\ frac {y (4z ^ {2} -x ^ {2} -y ^ {2})} {r ^ {3 } {\ sqrt {10}}}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ {3} ^ {- 1} + Y_ {3} ^ {1} \ right)}

$${\ displaystyle f_ {xyz} = N_ {3} ^ {c} {\ frac {xyz} {r ^ {3}}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ { 3} ^ {- 2} -Y_ {3} ^ {2} \ derecha)}

$${\ displaystyle f_ {z (x ^ {2} -y ^ {2})} = N_ {3} ^ {c} {\ frac {z \ left (x ^ {2} -y ^ {2} \ right )} {2r ^ {3}}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ {3} ^ {- 2} + Y_ {3} ^ {2} \ right)}

$${\ displaystyle f_ {x (x ^ {2} -3y ^ {2})} = N_ {3} ^ {c} {\ frac {x \ left (x ^ {2} -3y ^ {2} \ right )} {2r ^ {3} {\ sqrt {6}}}} = {\ frac {1} {\ sqrt {2}}} \ left (Y_ {3} ^ {- 3} -Y_ {3} ^ {3} \ derecha)}

$${\ displaystyle f_ {y (3x ^ {2} -y ^ {2})} = N_ {3} ^ {c} {\ frac {y \ left (3x ^ {2} -y ^ {2} \ right )} {2r ^ {3} {\ sqrt {6}}}} = {\ frac {i} {\ sqrt {2}}} \ left (Y_ {3} ^ {- 3} + Y_ {3} ^ {3} \ derecha)}

con

$${\ displaystyle N_ {3} ^ {c} = \ left ({\ frac {105} {4 \ pi}} \ right) ^ {1/2}}

f z 3	f xz 2	f yz 2	f xyz	f z (x 2 -y 2 )	f x (x 2 -3y 2 )	f y (3x 2 -y 2 )

Una ilustración de la ley de Dalton que usa los gases del aire al nivel del mar.

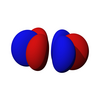En química y física, la ley de Dalton (también llamada ley de presiones parciales de Dalton ) establece que en una mezcla de gases que no reaccionan, la presión total ejercida es igual a la suma de las presiones parciales de los gases individuales. ^[1] Esta ley empírica fue observada por John Dalton en 1801 y publicada en 1802. ^[2] y está relacionada con las leyes del gas ideal .

Fórmula [ editar ]

Matemáticamente, la presión de una mezcla de gases no reactivos se puede definir como la suma:

$${\ displaystyle p _ {\ text {total}} = \ sum _ {i = 1} ^ {n} p_ {i}}       o      $${\ displaystyle p _ {\ text {total}} = p_ {1} + p_ {2} + p_ {3} + \ cdots + p_ {n}}

donde p ₁ , p ₂ , ..., p _n representan las presiones parciales de cada componente. ^[1]

$${\ displaystyle p_ {i} = p _ {\ text {total}} x_ {i}}

donde x _i es la fracción molar del componente i th en la mezcla total de n componentes.

Basado en el volumen de concentración [ editar ]

La siguiente relación proporciona una manera de determinar la concentración basada en el volumen de cualquier componente gaseoso individual

$${\ displaystyle p_ {i} = p _ {\ text {total}} c_ {i}}

donde c _i es la concentración del componente i th.

La ley de Dalton no es seguida estrictamente por gases reales, y la desviación aumenta con la presión. Bajo tales condiciones, el volumen ocupado por las moléculas se vuelve significativo en comparación con el espacio libre entre ellas. En particular, las distancias medias cortas entre moléculas aumentan las fuerzas intermolecularesentre las moléculas de gas lo suficiente como para cambiar sustancialmente la presión ejercida por ellas, un efecto no incluido en el modelo de gas ideal.