APUNTES DE GEODESIA

Una cuadrícula geodésica es una cuadrícula espacial basada en un poliedro geodésico o un poliedro de Goldberg .

Captura de pantalla de PYXIS WorldView que muestra una cuadrícula geodésica ISEA.

Construcción [ editar ]

Representación de volumen de la cuadrícula geodésica ^[1] aplicada en la simulación de la atmósfera utilizando el Modelo de resolución de la nube global (GCRM) ^[2] . La combinación de la ilustración de la rejilla y la representación de volumen de vorticidad (tubos amarillos). Tenga en cuenta que, a los efectos de una ilustración clara en la imagen, la cuadrícula es más gruesa que la real utilizada para generar la vorticidad.

El icosaedro

Un poliedro geodésico altamente dividido basado en el icosaedro.

Un poliedro Goldberg muy dividido : el doble de la imagen anterior.

Una cuadrícula geodésica es una referencia global de la Tierra que utiliza mosaicos triangulares basados ​​en la subdivisión de un poliedro (generalmente el icosaedro , y generalmente una subdivisión de Clase I) para subdividir la superficie de la Tierra. Dicha cuadrícula no tiene una relación directa con la latitud y la longitud, pero cumple con muchos de los criterios principales para una cuadrícula global discreta estadísticamente válida. ^[3] Principalmente, el área y la forma de las celdas son generalmente similares, especialmente cerca de los polos, donde muchas otras rejillas espaciales tienen singularidades o una gran distorsión. La popular Malla Triangular Cuaternaria (QTM) cae en esta categoría. ^[4]

Las grillas geodésicas pueden usar el poliedro dual del poliedrogeodésico, que es el poliedro de Goldberg . Los poliedros de Goldberg están formados por hexágonos y (si se basan en el icosaedro) 12 pentágonos. Una implementación que utiliza un icosaedro como el poliedro base, las células hexagonales y la proyección de área igual de Snyder se conoce como la cuadrícula de área igual de Snyder de icosaedro (ISEA). ^[5]

Aplicaciones [ editar ]

En la ciencia de la biodiversidad, las redes geodésicas son una extensión global de las redes locales discretas que se incluyen en estudios de campo para garantizar un muestreo estadístico adecuado y redes más grandes de usos múltiples desplegadas a nivel regional y nacional para desarrollar una comprensión global de la biodiversidad. Estas cuadrículas convierten los datos de monitoreo ambiental y ecológico de múltiples escalas espaciales y temporales en evaluaciones de la condición ecológica actual y pronósticos de riesgos para nuestros recursos naturales. Una cuadrícula geodésica permite la asimilación local a global de información ecológicamente significativa en su propio nivel de granularidad. ^[6]

Al modelar el clima , la circulación oceánica o el clima , se usan ecuaciones diferenciales parciales para describir la evolución de estos sistemas a lo largo del tiempo. Debido a que los programas de computadora se utilizan para construir y trabajar con estos modelos complejos, las aproximaciones deben formularse en formas fácilmente computables. Algunas de estas técnicas de análisis numérico (como las diferencias finitas ) requieren que el área de interés se subdivida en una cuadrícula, en este caso, sobre la forma de la Tierra .

Las grillas geodésicas pueden usarse en el desarrollo de videojuegospara modelar mundos ficticios en lugar de la Tierra. Son un análogo natural del mapa hexadecimal a una superficie esférica. ^[7]

Pros y contras [ editar ]

Pros:

• En gran parte isotrópica .
• La resolución se puede aumentar fácilmente por división binaria.
• No sufre el exceso de muestreo cerca de los polos, como las cuadrículas cuadradas más tradicionales de longitud-latitud.
• No produce sistemas lineales densos como lo hacen los métodos espectrales (vea también la cuadrícula gaussiana ).
• No hay puntos de contacto únicos entre las celdas de la cuadrícula vecinas. Las cuadrículas cuadradas y las cuadrículas isométricas sufren el problema ambiguo de cómo manejar a los vecinos que solo se tocan en un solo punto.
• Las celdas pueden estar tanto mínimamente distorsionadas como cerca del área. En contraste, las cuadrículas cuadradas no son de igual área, mientras que las cuadrículas rectangulares de igual área varían en forma desde el ecuador hasta los polos.

Contras:

• Más complicado de implementar que las cuadrículas rectangulares de longitud y latitud en las computadoras

Historia [ editar ]

El primer uso de la cuadrícula geodésica (icosaédrica) en modelos geofísicos se remonta a 1968 y el trabajo de Sadourny, Arakawa, Mintz ^[8] y Williamson. ^[9] [10] Trabajo posterior ampliado en esta base.

geodésicas en un elipsoide surgió en relación con la geodesia, específicamente con la solución de redes de triangulación . La figura de la Tierra está bien aproximada por unelipsoide oblato , una esfera ligeramente aplanada. Una geodésicaes la ruta más corta entre dos puntos en una superficie curva, análoga a una línea recta en una superficie plana. La solución de una red de triangulación en un elipsoide es, por lo tanto, un conjunto de ejercicios de trigonometría esferoidal ( Euler 1755 ).

Si la Tierra es tratada como una esfera , las geodésicas songrandes círculos (todos ellos cerrados) y los problemas se reducen a los de la trigonometría esférica . Sin embargo, Newton (1687)mostró que el efecto de la rotación de la Tierra hace que se asemeje a un elipsoide ligeramente oblato y, en este caso, elecuador y los meridianos son las únicas geodésicas cerradas simples. Además, el camino más corto entre dos puntos en el ecuador no se ejecuta necesariamente a lo largo del ecuador. Finalmente, si el elipsoide se perturba aún más para convertirse en un elipsoide triaxial(con tres semiejes distintos), solo se cierran tres geodésicas.

Una geodésica sobre un elipsoide oblato.

Geodésicos en un elipsoide de revolución [ editar ]

Hay varias formas de definir las geodésicas ( Hilbert y Cohn-Vossen 1952 , pp. 220–221). Una definición simple es como el camino más corto entre dos puntos en una superficie. Sin embargo, con frecuencia es más útil definirlos como trayectorias con curvatura geodésica cero , es decir, el análogo de las líneas rectas en una superficie curva. Esta definición abarca las geodésicas que viajan tan lejos a través de la superficie del elipsoide (algo más de la mitad de la circunferencia) que otras rutas distintas requieren menos distancia. A nivel local, estas geodésicas siguen siendo idénticas a la distancia más corta entre dos puntos.

A fines del siglo XVIII, un elipsoide de revolución (el término esferoide también se usa) fue una aproximación bien aceptada de la figura de la Tierra . El ajuste de las redes de triangulación conllevó la reducción de todas las mediciones a un elipsoide de referencia y la solución del problema bidimensional resultante como un ejercicio de trigonometría esferoidal ( Bomford 1952 , capítulo 3) ( Leick et al. 2015 , §4.5).

Fig. 1. Un AB geodésico en un elipsoide de revolución. N es el polo norte y EFH se encuentra en el ecuador.

Es posible reducir los diversos problemas geodésicos en uno de dos tipos. Considere dos puntos: A en la latitud φ ₁ y longitud λ ₁ y B en la latitud φ ₂ y longitud λ ₂ (ver Fig. 1). La conexión geodésica (de A a B ) es AB , de longitud s ₁₂ , que tiene acimutes α ₁ y α ₂ en los dos puntos finales. ^[1] Los dos problemas geodésicos generalmente considerados son:

1. el problema geodésico directo o el primer problema geodésico , dados A , α ₁ y s ₁₂ , determinan B y α ₂ ;
2. El problema geodésico inverso o segundo problema geodésico , dados A y B , determinan s ₁₂ , α ₁ y α ₂ .

Como puede verse en la Fig. 1, estos problemas implican resolver el triángulo NAB dado un ángulo, α ₁ para el problema directo y λ ₁₂ = λ ₂ - λ ₁ para el problema inverso, y sus dos lados adyacentes. Para una esfera, las soluciones a estos problemas son ejercicios simples en trigonometría esférica , cuya solución está dada porfórmulas para resolver un triángulo esférico . (Vea el artículo sobre la navegación en gran círculo .)

Para un elipsoide de revolución, Clairaut (1735) encontró la constante característica que define la geodésica . Legendre (1806) y Oriani (1806) dieron una solución sistemática para los caminos de las geodésicas (y documentos posteriores en 1808 y 1810 ). Bessel (1825) da la solución completa para el problema directo (completa con tablas computacionales y un ejemplo resuelto ) .

Durante el siglo XVIII, las geodésicas se denominaban típicamente "líneas más cortas". El término "línea geodésica" fue acuñado por Laplace (1799b) :

Nous désignerons cette ligne sous le nom de ligne géodésique [Llamaremos a esta línea la línea geodésica ].

Esta terminología se introdujo en inglés como "línea geodésica" o como "línea geodésica", por ejemplo ( Hutton 1811 ),

Una línea trazada de la manera que ahora hemos estado describiendo, o deducida a partir de medidas trigonométricas, por los medios que hemos indicado, se llama línea geodésica o geodésica:tiene la propiedad de ser la más corta que se puede dibujar entre sus dos extremidades en la superficie de la tierra; y, por lo tanto, es la medida adecuada del itinerario de la distancia entre esos dos puntos.

En su adopción por otros campos se prefirió la línea geodésica , frecuentemente acortada a geodésica .

Esta sección trata el problema en un elipsoide de revolución (tanto oblato como prolado). El problema en un elipsoide triaxial se trata en la siguiente sección.

Las ecuaciones para una geodésica [ editar ]

Fig. 2. Elemento diferencial de una elipse meridiana.

Fig. 3. Elemento diferencial de una geodésica en un elipsoide.

Aquí se desarrollan las ecuaciones para una geodésica; La derivación sigue de cerca la de Bessel (1825) .Jordan & Eggert (1941) , Bagratuni (1962 , §15), Gan'shin (1967 , Cap. 5), Krakiwsky & Thomson (1974 , §4), Rapp (1993 , §1.2), Jekeli (2012) , y Borre y Strang (2012)también proporcionan derivaciones de estas ecuaciones.

Considere un elipsoide de revolución con un radio ecuatorial a y unsemieje polar b . Defina el aplanamiento f = ( a - b ) / a , la excentricidad e = √ a ² - b ² / a = √ f (2 - f ) , y la segunda excentricidad e ′ = √ a ² - b ² / b = e / (1 - f ). (En la mayoría de las aplicaciones en geodesia, se considera que el elipsoide está oblato, a > b ; sin embargo, la teoría se aplica sin cambio a los elipsoides prolados, a < b , en cuyo caso f , e ² y e ′ ² son negativos).

Deje que un segmento elemental de un camino en el elipsoide tenga una longitud ds . De las Figs. 2 y 3, vemos que si su acimut es α , entonces ds está relacionado con d φ y d λ por

(1)$${\ displaystyle {\ color {blanco}.} \ qquad \ cos \ alpha \, ds = \ rho \, d \ varphi = - {\ frac {dR} {\ sin \ varphi}}, \ quad \ sin \ alpha \, ds = R \, d \ lambda,}

donde ρ es el radio de curvatura meridional , R = ν cosφ es el radio del círculo de latitud φ , y ν es el radio de curvatura normal . El segmento elemental es por lo tanto dado por

$${\ displaystyle ds ^ {2} = \ rho ^ {2} \, d \ varphi ^ {2} + R ^ {2} \, d \ lambda ^ {2}}

o

{\ displaystyle {\ begin {alineado} ds & = {\ sqrt {\ rho ^ {2} \ varphi '^ {2} + R ^ {2}}} \, d \ lambda \\ & \ equiv L (\ varphi , \ varphi ') \, d \ lambda, \ end {alineado}}}

donde φ ′ = d φ / d λ y la función lagrangiana L depende de φ a ρ (φ) y R (φ) . La longitud de una ruta arbitraria entre (φ ₁ , λ ₁ ) y (φ ₂ , λ ₂ ) viene dada por

$${\ displaystyle s_ {12} = \ int _ {\ lambda _ {1}} ^ {\ lambda _ {2}} L (\ varphi, \ varphi ') \, d \ lambda,}

donde φ es una función de λ que satisface φ (λ ₁ ) = φ ₁ y φ (λ ₂ ) = φ ₂ . El camino más corto o geodésico implica encontrar esa función φ (λ) que minimiza s ₁₂ . Este es un ejercicio en el cálculo de variaciones y la condición de minimización viene dada por la identidad de Beltrami ,

$${\ displaystyle L- \ varphi '{\ frac {\ partial L} {\ partial \ varphi'}} = {\ text {const.}}}

Sustituyendo por L y utilizando las ecuaciones. (1) da

$${\ displaystyle R \ sin \ alpha = {\ text {const.}}}

Clairaut (1735) encontró esta relación , utilizando una construcción geométrica; Lyusternik (1964 , §10) presenta una derivación similar . ^{[2] La} diferenciación de esta relación da

$${\ displaystyle d \ alpha = \ sin \ varphi \, d \ lambda.}

Esto, junto con las ecs. (1), conduce a un sistema de ecuaciones diferenciales ordinarias para una geodésica

$${\ displaystyle {\ color {blanco}.} \ qquad {\ frac {d \ varphi} {ds}} = {\ frac {\ cos \ alpha} {\ rho}}; \ quad {\ frac {d \ lambda } {ds}} = {\ frac {\ sin \ alpha} {\ nu \ cos \ varphi}}; \ quad {\ frac {d \ alpha} {ds}} = {\ frac {\ tan \ varphi \ sin \ alpha} {\ nu}}.}

Podemos expresar R en términos de la latitud paramétrica , β , usando

$${\ displaystyle R = a \ cos \ beta,}

y la relación de Clairaut se convierte entonces en

$${\ displaystyle \ sin \ alpha _ {1} \ cos \ beta _ {1} = \ sin \ alpha _ {2} \ cos \ beta _ {2}.}

Fig. 4. Problema geodésico mapeado a la esfera auxiliar.

Fig. 5. El problema geodésico elemental en la esfera auxiliar.

Esta es la regla sinusoidal de la trigonometría esférica relacionando dos lados del triángulo NAB , (ver Fig. 4) NA = ¹ / ₂ π - ß ₁ , yNB = ¹ / ₂ π - ß ₂ y sus ángulos opuestos B = π - α ₂ y A = α ₁ .

Para encontrar la relación para el tercer lado AB = σ ₁₂ , la longitud del arco esférico y el ángulo incluido N = ω ₁₂ , la longitud esférica , es útil considerar el triángulo NEP que representa una geodésica que comienza en el ecuador; vea la Fig. 5. En esta figura, las variables referidas a la esfera auxiliar se muestran con las cantidades correspondientes para el elipsoide que se muestran entre paréntesis. Las cantidades sin subíndices se refieren al punto arbitrario P ; E , el punto en el que la geodésica cruza el ecuador en dirección hacia el norte, se utiliza como el origen para σ , sy ω .

Fig. 6. Elemento diferencial de una geodésica en una esfera.

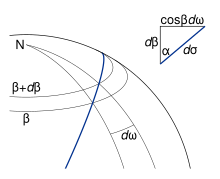
Si el lado EP se extiende al mover P infinitesimalmente (ver Fig. 6), obtenemos

(2)$${\ displaystyle {\ color {blanco}.} \ qquad \ cos \ alpha \, d \ sigma = d \ beta, \ quad \ sin \ alpha \, d \ sigma = \ cos \ beta \, d \ omega.}

Combinando ecuaciones. (1) y (2) da ecuaciones diferenciales para s y λ

$${\ displaystyle {\ frac {1} {a}} {\ frac {ds} {d \ sigma}} = {\ frac {d \ lambda} {d \ omega}} = {\ frac {\ sin \ beta} {\ sin \ varphi}}.}

La relación entre β y φ es

$${\ displaystyle \ tan \ beta = {\ sqrt {1-e ^ {2}}} \ tan \ varphi = (1-f) \ tan \ varphi,}

lo que da

$${\ displaystyle {\ frac {\ sin \ beta} {\ sin \ varphi}} = {\ sqrt {1-e ^ {2} \ cos ^ {2} \ beta}},}

Para que las ecuaciones diferenciales de la geodésica se conviertan

$${\ displaystyle {\ frac {1} {a}} {\ frac {ds} {d \ sigma}} = {\ frac {d \ lambda} {d \ omega}} = {\ sqrt {1-e ^ { 2} \ cos ^ {2} \ beta}}.}

El último paso es usar σ como el parámetro independiente en ambas ecuaciones diferenciales y, por lo tanto, expresar s y λ como integrales. La aplicación de la regla sinusoidal a los vértices E y G en el triángulo esféricoEGP en la Fig. 5 da

$${\ displaystyle \ sin \ beta = \ sin \ beta (\ sigma; \ alpha _ {0}) = \ cos \ alpha _ {0} \ sin \ sigma,}

donde α ₀ es el acimut en E . Sustituyendo esto en la ecuación de ds / d σ e integrando el resultado da

(3)$${\ displaystyle {\ color {blanco}.} \ qquad {\ frac {s} {b}} = \ int _ {0} ^ {\ sigma} {\ sqrt {1 + k ^ {2} \ sin ^ { 2} \ sigma '}} \, d \ sigma',}

dónde

$${\ displaystyle k = e '\ cos \ alpha _ {0},}

y los límites de la integral se eligen de modo que s (σ = 0) = 0 . Legendre (1811 , p. 180) señaló que la ecuación para s es la misma que la ecuación para el arco en una elipse con semiejes b √ 1 + e ′ ² cos ² α ₀ y b . Para expresar la ecuación de λ en términos de σ , escribimos

$${\ displaystyle d \ omega = {\ frac {\ sin \ alpha _ {0}} {\ cos ^ {2} \ beta}} \, d \ sigma,}

que sigue de la ec. (2) y la relación de Clairaut. Esto produce

(4)$${\ displaystyle {\ color {blanco}.} \ qquad \ lambda - \ lambda _ {0} = \ omega -f \ sin \ alpha _ {0} \ int _ {0} ^ {\ sigma} {\ frac { 2-f} {1+ (1-f) {\ sqrt {1 + k ^ {2} \ sin ^ {2} \ sigma '}}}} \, d \ sigma',}

y los límites de las integrales se eligen de modo que λ = λ ₀ en el cruce del ecuador, σ = 0 .

Esto completa la solución de la ruta de una geodésica utilizando la esfera auxiliar. Mediante este dispositivo, se puede asignar un gran círculo exactamente a una geodésica en un elipsoide de revolución.

También hay varias formas de aproximar las geodésicas en un elipsoide terrestre (con un aplanamiento pequeño) ( Rapp 1991 , §6); Algunos de estos se describen en el artículo sobre la distancia geográfica . Sin embargo, estos son típicamente comparables en complejidad al método para la solución exacta ( Jekeli 2012 , §2.1.4).

Comportamiento de las geodésicas [ editar ]

Fig. 7. Los meridianos y el ecuador son las únicas geodésicas cerradas. (Para los elipsoides muy aplanados, hay otras geodésicas cerradas; vea las figuras 11 y 12).

Geodésica sobre un elipsoide achatado ( f = ¹ / ₅₀ ) con α ₀ =45 ° .

Fig. 8. Siguiendo la geodésica en el elipsoide durante aproximadamente 5 circuitos.

Fig. 9. La misma geodésica después de unos 70 circuitos.

Fig. 10. geodésica en un elipsoide prolato ( f = - ¹ / ₅₀ ) con α ₀ =45 ° . Compare con la Fig. 8.

La Fig. 7 muestra las geodésicas cerradas simples que consisten en los meridianos (verde) y el ecuador (rojo). (Aquí, la calificación "simple" significa que la geodésica se cierra sobre sí misma sin una intersección de autointervención.) Esto se deduce de las ecuaciones para las geodésicas dadas en la sección anterior.

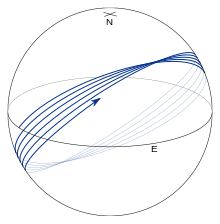
Todas las demás geodésicas están tipificadas en las Figs. 8 y 9 que muestran un inicio geodésico en el ecuador con α ₀ = 45 ° . La geodésica oscila sobre el ecuador. Los cruces ecuatoriales se llaman nodos y los puntos de latitud máxima o mínima se llaman vértices ; las latitudes de vértices están dadas por β = ± ( ¹ / ₂ π - | α ₀ |) . La geodésica completa una oscilación completa en latitud antes de que la longitud haya aumentado en360 ° . Por lo tanto, en cada cruce sucesivo hacia el norte del ecuador (ver Fig. 8), λ no llega a un circuito completo del ecuador en aproximadamente 2π f sinα ₀ (para un elipsoide prolato, esta cantidad es negativa y λ completa más que un total circuito; ver fig. 10). Para casi todos los valores de α ₀ , la geodésica llenará esa parte del elipsoide entre las dos latitudes del vértice (ver Fig. 9).

Dos geodésicas cerradas adicionales para el elipsoide achatado, ^b / _a = ² / ₇ .

Fig. 11. Vista lateral.

Fig. 12. Vista superior.

Si el elipsoide es suficientemente achatado, es decir, ^b / _a < ¹ / ₂ , otra clase de geodésicas simples cerradas es posible ( Klingenberg 1982 , §3.5.19). Dos de estas geodésicas se ilustran en las Figs. 11 y 12. Aquí ^b / _a = ² / ₇ y el acimut ecuatorial, α ₀ , para el verde (resp. Azul) geodésica es elegido para ser53.175 ° (resp.75.192 ° ), de modo que la geodésica completa 2 (resp. 3) oscilaciones completas sobre el ecuador en un circuito del elipsoide.

Fig. 13. Geodesics (azul) desde un único punto para f = ¹ / ₁₀ , φ ₁ =−30 ° ; Los círculos geodésicos se muestran en verde y el lugar de corte en rojo.

La Fig. 13 muestra las geodésicas (en azul) que emanan A con α ₁ un múltiplo de 15 ° hasta el punto en el que dejan de ser caminos más cortos. (El aplanamiento se ha aumentado a ¹ / ₁₀ con el fin de acentuar los efectos elipsoidales.) También se muestra (en verde) son curvas de constante s ₁₂ , que son los círculos geodésicas centrados A . Gauss (1828) mostró que, en cualquier superficie, las geodésicas y los círculos geodésicos se intersecan en ángulos rectos. La línea roja es el locus de corte , el lugar geométrico de puntos que tienen múltiples (dos en este caso) geodésicas más cortas desde A . En una esfera, el lugar de corte es un punto. En un elipsoide oblato (que se muestra aquí), es un segmento del círculo de latitud centrado en el punto antípodas a A , φ = −φ ₁ . La extensión longitudinal del lugar del corte es aproximadamenteλ ₁₂ ∈ [π - f π cosφ ₁ , π + f π cosφ ₁ ] . Si A se encuentra en el ecuador, φ ₁ = 0 , esta relación es exacta y, como consecuencia, el ecuador es solo una geodésica más corta si | λ ₁₂ | ≤ (1 - f ) π . Para un elipsoide prolado, el lugar del corte es un segmento del anti-meridiano centrado en el punto antipodal a A , λ ₁₂ = π, y esto significa que las geodésicas meridionales dejan de ser caminos más cortos antes de que se alcance el punto antípodas.