ARTÍCULOS DE ESTADÍSTICA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El 95% del área bajo la distribución normal se encuentra dentro de 1.96 desviaciones estándar de la media.

En probabilidad y estadísticas , 1.96 es el valor aproximado del punto de percentil 97.5 de la distribución normal . El 95% del área bajo una curva normal se encuentra dentro de aproximadamente 1.96 desviaciones estándar de la media y, debido al teorema del límite central , este número se usa en la construcción de intervalos de confianza aproximados del 95% . Su ubicuidad se debe a la convención arbitraria pero común de utilizar intervalos de confianza con una cobertura del 95% en lugar de otras coberturas (como el 90% o el 99%). ^{[1] [2] [3] [4]}Esta convención parece particularmente común en las estadísticas médicas, ^{[5] [6] [7],} pero también es común en otras áreas de aplicación, como las ciencias de la tierra, ^[8]ciencias sociales e investigación empresarial. ^[9]

No hay un solo nombre aceptado para este número; También se conoce comúnmente como el "estándar normal de desviación ", " puntuación normal " o " puntuación Z " para el punto 97.5 percentil, o 0,975 punto.

Si X tiene una distribución normal estándar, es decir, X ~ N (0,1),

{\ displaystyle \ mathrm {P} (X> 1.96) \ approx 0.025, \,}

{\ displaystyle \ mathrm {P} (X <1 .96="" 0.975="" approx="" font="">

y como la distribución normal es simétrica,

{\ displaystyle \ mathrm {P} (-1.96

Una notación para este número es z _.975 . ^[10] A partir de la función de densidad de probabilidad de la distribución normal estándar, el valor exacto de z _.975 se determina por

$${\ displaystyle {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {z _ {. 975}} e ^ {- x ^ {2} / 2} \, \ mathrm {d} x = 0.975.}

Historia [ editar ]

Ronald Fisher

El uso de este número en las estadísticas aplicadas puede atribuirse a la influencia del libro de texto clásico de Ronald Fisher , Métodos estadísticos para investigadores , publicado por primera vez en 1925:

"El valor para el que P = .05, o 1 en 20, es 1.96 o casi 2; es conveniente tomar este punto como un límite para juzgar si una desviación debe considerarse significativa o no". ^[11]

En la tabla 1 del mismo trabajo, dio el valor más preciso 1.959964. ^[12] En 1970, el valor truncado a 20 lugares decimales se calculó para ser

1.95996 39845 40054 23552 ... ^[13]

El valor aproximado comúnmente utilizado de 1.96 es, por lo tanto, más preciso que una parte en 50,000, lo que es más que adecuado para el trabajo aplicado.

Algunas personas incluso utilizan el valor de 2 en lugar de 1.96, informando un intervalo de confianza del 95,4% como un intervalo de confianza del 95%. Esto no es recomendable, pero puede que lo veas ocasionalmente. ^[14]

Funciones de software [ editar ]

La inversa de la CDF normal estándar puede usarse para calcular el valor. La siguiente es una tabla de llamadas a funciones que devuelven 1.96 en algunas aplicaciones de uso común:

Solicitud	Llamada de función
Sobresalir	NORM.S.INV ( 0.975 )
MATLAB	norminv ( 0.975 )
R	qnorm ( 0.975 )
scipy	scipy.stats.norm.ppf ( 0.975 )
SAS	probit (0,025);
SPSS	x = IDF.NORMAL COMPUTO (0.975,0,1).
Stata	anormal ( 0.975 )
Wolfram Language ( Mathematica )	InverseCDF [NormalDistribution [0, 1], 0.975]

En estadística , econometría , epidemiología y disciplinas relacionadas, el método de las variables instrumentales ( IV ) se utiliza para estimar relaciones causales cuando los experimentos controlados no son factibles o cuando un tratamiento no se administra con éxito a cada unidad en un experimento aleatorio. ^[1]Intuitivamente, las IV se utilizan cuando una variable explicativa de interés se correlaciona con el término de error, en cuyo caso los mínimos cuadrados ordinarios y ANOVA dan sesgadosresultados Un instrumento válido induce cambios en la variable explicativa pero no tiene un efecto independiente en la variable dependiente, lo que permite que un investigador descubra el efecto causal de la variable explicativa en la variable dependiente.

Los métodos de variables instrumentales permiten una estimación consistente cuando las variables explicativas(covariables) se correlacionan con los términos de error en un modelo de regresión . Dicha correlación puede ocurrir 1) cuando los cambios en la variable dependiente cambian el valor de al menos una de las covariables(causalidad "inversa"), 2) cuando hay variables omitidas que afectan tanto a las variables dependientes como a las independientes, o 3) cuando Las covariables están sujetas a errores de medición no aleatorios . Las variables explicativas que sufren uno o más de estos problemas en el contexto de una regresión a veces se denominan endógenas.. En esta situación, los mínimos cuadrados ordinarios producen estimaciones sesgadas e inconsistentes. ^[2] Sin embargo, si hay un instrumento disponible, aún se pueden obtener estimaciones consistentes. Un instrumento es una variable que no pertenece a la ecuación explicativa, sino que se correlaciona con las variables explicativas endógenas , condicionales al valor de otras covariables.

En los modelos lineales, existen dos requisitos principales para el uso de IV:

• El instrumento debe estar correlacionado con las variables explicativas endógenas, condicionalmente en las otras covariables. Si esta correlación es fuerte, entonces se dice que el instrumento tiene una primera etapa fuerte . Una correlación débil puede proporcionar inferencias engañosas sobre las estimaciones de los parámetros y los errores estándar. ^[3]
• El instrumento no puede correlacionarse con el término de error en la ecuación explicativa, condicionalmente en las otras covariables. En otras palabras, el instrumento no puede sufrir el mismo problema que la variable predictiva original. Si se cumple esta condición, se dice que el instrumento satisface la restricción de exclusión .

Introducción [ editar ]

El concepto de variables instrumentales fue derivado por primera vez por Philip G. Wright, posiblemente en coautoría con su hijo Sewall Wright , en el contexto de ecuaciones simultáneas en su libro de 1928 The Tariff on Animal and Vegetable Oils . ^[4] [5] En 1945, Olav Reiersøl aplicó el mismo enfoque en el contexto de los modelosde errores en las variables en su disertación, dando nombre al método. ^[6]

Mientras que las ideas detrás de IV se extienden a una amplia clase de modelos, un contexto muy común para IV es en regresión lineal. Tradicionalmente, ^[7] una variable instrumental se define como una variable Z que se correlaciona con la variable independiente X y no se correlaciona con el "término de error" U en la ecuación lineal

$${\ displaystyle Y = X \ beta + U}

Tenga en cuenta que $${\ displaystyle X}es una matriz, generalmente con una columna de unos y quizás con columnas adicionales para otras covariables. Considere cómo un instrumento resuelve este problema. Recordemos que OLS resuelve para$${\ displaystyle {\ widehat {\ beta}}} tal que $${\ displaystyle \ operatorname {cov} (X, {\ widehat {U}}) = 0} (Cuando minimizamos la suma de errores al cuadrado, $${\ displaystyle \ min _ {\ widehat {\ beta}} (Y - {\ widehat {\ beta}} X) '(Y - {\ widehat {\ beta}} X)}, la condición de primer orden es exactamente $${\ displaystyle X '(Y - {\ widehat {\ beta}} X) = X' {\ widehat {U}} = 0}.) Si se cree que el modelo verdadero tiene $${\ displaystyle \ operatorname {cov} (X, U) \ neq 0}debido a cualquiera de las razones enumeradas anteriormente, por ejemplo, si hay una variable omitida que afecta tanto a$${\ displaystyle X} y $${\ displaystyle Y}por separado, entonces este procedimiento OLS no producirá el impacto causal de$${\ displaystyle X} en $${\ displaystyle Y}. OLS simplemente seleccionará el parámetro que hace que los errores resultantes aparezcan sin correlación con$${\ displaystyle X}.

Consideremos por simplicidad el caso de una sola variable. Supongamos que estamos considerando una regresión con una variable y una constante (tal vez no sean necesarias otras covariables, o tal vez hayamos incluido otras covariables relevantes):

$${\ displaystyle y = \ alpha + \ beta x + u}

En este caso, el coeficiente en el regresor de interés está dado por $${\ displaystyle {\ widehat {\ beta}} = {\ frac {\ operatorname {cov} (x, y)} {\ operatorname {var} (x)}}}. ^[8] Sustituyendo a$${\ displaystyle y} da

{\ displaystyle {\ begin {alineado} {\ widehat {\ beta}} & = {\ frac {\ operatorname {cov} (x, y)} {\ operatorname {var} (x)}} = {\ frac { \ operatorname {cov} (x, \ alpha + \ beta x + u)} {\ operatorname {var} (x)}} \\ [6pt] & = {\ frac {\ operatorname {cov} (x, \ alpha + \ beta x)} {\ operatorname {var} (x)}} + {\ frac {\ operatorname {cov} (x, u)} {\ operatorname {var} (x)}} = \ beta ^ {* } + {\ frac {\ operatorname {cov} (x, u)} {\ operatorname {var} (x)}}, \ end {alineado}}}

dónde $${\ displaystyle \ beta ^ {*}}es lo que sería el vector de coeficiente estimado si x no estuviera correlacionado con u . Se puede demostrar que$${\ displaystyle \ beta ^ {*}} sería un estimador imparcial de $${\ displaystyle \ beta.} Si $${\ displaystyle \ operatorname {cov} (x, u) \ neq 0}en el modelo subyacente que creemos, entonces OLS proporciona un coeficiente que no refleja el efecto causal subyacente del interés. IV ayuda a solucionar este problema identificando los parámetros$${\ displaystyle {\ vec {\ beta}}} no basado en si $${\ displaystyle x} no está correlacionado con $${\ displaystyle u}, pero en función de si otra variable $${\ displaystyle z} (o conjunto de variables) no está correlacionado con $${\ displaystyle u}. Si la teoría sugiere que$${\ displaystyle z} está relacionado con $${\ displaystyle x} (la primera etapa) pero no correlacionada con $${\ displaystyle u}(la restricción de exclusión), entonces IV puede identificar el parámetro causal de interés donde OLS falla. Debido a que existen múltiples formas específicas de usar y derivar estimadores IV incluso en el caso lineal (IV, 2SLS, GMM), guardamos más información para la sección de Estimación a continuación.

Por supuesto, las técnicas IV se han desarrollado en una clase mucho más amplia de modelos no lineales. Pearl (2000; p. 248) dio definiciones generales de variables instrumentales, utilizando formalismo contrafactual y gráfico. ^[9] La definición gráfica requiere que Z cumpla con las siguientes condiciones:

$${\ displaystyle (Z \ perp \! \! \! \ perp Y) _ {G _ {\ overline {X}}} \ qquad (Z \ not \! \! {\ perp \! \! \! \ perp} X) _ {G}}

dónde $${\ displaystyle \ perp \! \! \! \ perp}representa la separación d ^[10] y$${\ displaystyle G _ {\ overline {X}}}representa la gráfica en la que se cortan todas las flechas que entran en X.

La definición contrafactual requiere que Z satisfaga

$${\ displaystyle (Z \ perp \! \! \! \ perp Y_ {x}) \ qquad (Z \ not \! \! {\ perp \! \! \! \ perp} X)}

donde Y _x representa el valor que Y obtendría si X hubiera sido x y$${\ displaystyle \ perp \! \! \! \ perp} representa la independencia.

Si hay covariables adicionales W a continuación las definiciones anteriores se modifican de manera que Z califica como un instrumento si los criterios dados tienen condicional en W .

La esencia de la definición de Pearl es:

1. Las ecuaciones de interés son "estructurales", no "regresión".
2. El término de error U representa todos los factores exógenos que afectan a Y cuando X se mantiene constante.
3. El instrumento Z debe ser independiente de U.
4. El instrumento Z no debería afectar a Y cuando X se mantiene constante (restricción de exclusión).
5. El instrumento Z no debe ser independiente de X.

Estas condiciones no se basan en la forma funcional específica de las ecuaciones y, por lo tanto, son aplicables a las ecuaciones no lineales, donde U puede ser no aditiva (ver Análisis no paramétrico). También son aplicables a un sistema de múltiples ecuaciones, en el que X (y otros factores) afectan a Y a través de varias variables intermedias. Tenga en cuenta que una variable instrumental no tiene por qué ser una causa de X ; También se puede usar un proxy de tal causa, si cumple con las condiciones 1-5. ^[9] Tenga en cuenta también que la restricción de exclusión (condición 4) es redundante; se desprende de las condiciones 2 y 3.

Ejemplo [ editar ]

De manera informal, en el intento de estimar el efecto causal de alguna variable X en otro Y , un instrumento es una tercera variable Z que afecta Y sólo a través de su efecto sobre la  X . Por ejemplo, supongamos que un investigador desea estimar el efecto causal del hábito de fumar en la salud general. ^[11] La correlación entre la salud y el hábito de fumar no implica que fumar cause una mala salud porque otras variables, como la depresión, pueden afectar tanto la salud como el hábito de fumar, o porque la salud puede afectar el hábito de fumar. En el mejor de los casos, es difícil y costoso realizar experimentos controlados sobre el estado del tabaquismo en la población general. El investigador puede intentar estimar el efecto causal del hábito de fumar en la salud a partir de los datos de observación utilizando la tasa impositiva para los productos de tabaco como instrumento para fumar. La tasa impositiva para los productos de tabaco es una opción razonable para un instrumento porque el investigador asume que solo puede correlacionarse con la salud a través de su efecto sobre el hábito de fumar. Si el investigador luego encuentra que los impuestos al tabaco y el estado de salud están correlacionados, esto puede verse como evidencia de que fumar causa cambios en la salud.

Angrist y Krueger (2001) presentan una revisión de la historia y los usos de las técnicas de variables instrumentales. ^[12]

Seleccionando instrumentos adecuados [ editar ]

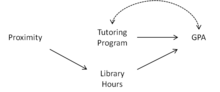
Dado que U no se observa, el requisito de que Z sea ​​independiente de U no puede deducirse de los datos y, en cambio, debe determinarse a partir de la estructura del modelo, es decir, el proceso de generación de datos. Gráficos causales son una representación de esta estructura, y la definición gráfica dada anteriormente se pueden utilizar para determinar rápidamente si una variable Z califica como una variable instrumental dado un conjunto de covariables W . Para ver cómo, considere el siguiente ejemplo.

Figura 1: la proximidad califica como una variable instrumental dada las horas de biblioteca

Figura 2: $${\ displaystyle G _ {\ overline {X}}}, que se utiliza para determinar si la proximidad es una variable instrumental.

Figura 3: la proximidad no califica como una variable instrumental dada las horas de biblioteca

Figura 4: La proximidad califica como una variable instrumental, siempre y cuando no incluyamos las Horas de la Biblioteca como una covariable.

Supongamos que deseamos estimar el efecto de un programa de tutoría universitaria en el promedio de calificaciones ( GPA ). La relación entre asistir al programa de tutoría y el GPA puede verse confundida por una serie de factores. Los estudiantes que asisten al programa de tutoría pueden preocuparse más por sus calificaciones o pueden estar luchando con su trabajo. Esta confusión se muestra en las Figuras 1-3 a la derecha a través del arco bidireccionado entre el Programa de Tutoría y el GPA. Si los estudiantes son asignados a dormitorios al azar, la proximidad del dormitorio del estudiante al programa de tutoría es un candidato natural para ser una variable instrumental.

Sin embargo, ¿qué sucede si el programa de tutoría se encuentra en la biblioteca de la universidad? En ese caso, la proximidad también puede hacer que los estudiantes pasen más tiempo en la biblioteca, lo que a su vez mejora su GPA (consulte la Figura 1). Usando el gráfico causal que se muestra en la Figura 2, vemos que la Proximidad no califica como una variable instrumental porque está conectada al GPA a través de la Proximidad del camino.$${\ displaystyle \ rightarrow} Horas de la biblioteca $${\ displaystyle \ rightarrow} GPA en $${\ displaystyle G _ {\ overline {X}}}. Sin embargo, si controlamos las Horas de la Biblioteca agregándolas como una covariable, entonces la Proximidad se convierte en una variable instrumental, ya que la Proximidad se separa del GPA dado en las Horas de la Biblioteca en$${\ displaystyle G _ {\ overline {X}}}^{[ cita requerida ]} .

Ahora, supongamos que notamos que la "habilidad natural" de un estudiante afecta su número de horas en la biblioteca, así como su GPA, como en la Figura 3. Al usar el gráfico causal, vemos que las Horas de la Biblioteca son un colector y Acondicionado sobre él abre el camino proximidad. $${\ displaystyle \ rightarrow} Horas de la biblioteca $${\ displaystyle \ leftrightarrow}GPA. Como resultado, la proximidad no se puede utilizar como una variable instrumental.

Finalmente, supongamos que las Horas de la Biblioteca no afectan realmente el GPA porque los estudiantes que no estudian en la biblioteca simplemente estudian en otra parte, como en la Figura 4. En este caso, el control de las Horas de la Biblioteca aún abre un camino espurio desde la Proximidad al GPA. Sin embargo, si no controlamos las Horas de la Biblioteca y las eliminamos como una covariable, entonces la Proximidad puede usarse nuevamente como una variable instrumental.

Estimación [ editar ]

Ahora revisamos y ampliamos la mecánica de IV en mayor detalle. Supongamos que los datos son generados por un proceso del formulario.

$${\ displaystyle y_ {i} = X_ {i} \ beta + e_ {i},}

dónde

• i indexa observaciones,
• $${\ displaystyle y_ {i}}es el i -ésimo valor de la variable dependiente,
• $${\ displaystyle X_ {i}}es un vector de los valores i -th de la (s) variable (s) independiente (s) y una constante,
• $${\ displaystyle e_ {i}}es el i -ésimo valor de un término de error no observado que representa todas las causas de$${\ displaystyle y_ {i}} otro que $${\ displaystyle X_ {i}}y
• $${\ displaystyle \ beta} Es un vector de parámetro no observado.

El vector parametro $${\ displaystyle \ beta} es el efecto causal sobre $${\ displaystyle y_ {i}} de un cambio de una unidad en cada elemento de $${\ displaystyle X_ {i}}, sosteniendo todas las otras causas de $${\ displaystyle y_ {i}}constante. El objetivo econométrico es estimar.$${\ displaystyle \ beta}. En aras de la simplicidad, supongamos que los trazos de e no están correlacionados y que se extraen de distribuciones con la misma varianza (es decir, que los errores son no correlacionados en serie y son homoskedastic ).

Supongamos también que se propone un modelo de regresión nominal de la misma forma. Dada una muestra aleatoria de T observaciones de este proceso, el estimador de mínimos cuadrados ordinario es

$${\ displaystyle {\ widehat {\ beta}} _ {\ mathrm {OLS}} = (X'X) ^ {- 1} X'y = (X'X) ^ {- 1} X '(X \ beta + e) = \ beta + (X'X) ^ {- 1} X'e}

donde X , Y y e vectores columna denotan de longitud T . Note la similitud de esta ecuación con la ecuación que involucra$${\ displaystyle \ operatorname {cov} (X, y)}en la introducción (esta es la versión matricial de esa ecuación). Cuando X y e no están correlacionados , bajo ciertas condiciones de regularidad, el segundo término tiene un valor esperado condicional en X de cero y converge a cero en el límite, por lo que el estimador es imparcial y consistente. Sin embargo, cuando X y las otras variables causales no medidas se colapsaron en el término e, se correlacionan, sin embargo, el estimador OLS generalmente está sesgado e inconsistente para  β . En este caso, es válido usar las estimaciones para predecir valores de y valores dados de X, pero la estimación no recupera el efecto causal de Xen  y .

Para recuperar el parámetro subyacente $${\ displaystyle \ beta}, introducimos un conjunto de variables Z que está altamente correlacionado con cada componente endógeno de X pero (en nuestro modelo subyacente) no está correlacionado con  e . Para simplificar, se podría considerar que X es una matriz T × 2 compuesta por una columna de constantes y una variable endógena, y que Z es una T × 2 que consiste en una columna de constantes y una variable instrumental. Sin embargo, esta técnica generaliza a que X es una matriz de una constante y, digamos, 5 variables endógenas, siendo Z una matriz compuesta de una constante y 5 instrumentos. En la discusión que sigue, asumiremos queX es una matriz T × K y deja este valor K sin especificar. Un estimador en el que X y Z son matrices de T × K se conoce como recién identificado .

Supongamos que la relación entre cada componente endógeno x _i , y los instrumentos está dada por

$${\ displaystyle x_ {i} = Z_ {i} \ gamma + v_ {i},}

La especificación IV más común utiliza el siguiente estimador:

$${\ displaystyle {\ widehat {\ beta}} _ {\ mathrm {IV}} = (Z'X) ^ {- 1} Z'y}

Tenga en cuenta que esta especificación se aproxima al verdadero parámetro a medida que la muestra se hace grande, siempre que $${\ displaystyle Z'e = 0} en el modelo verdadero:

$${\ displaystyle {\ widehat {\ beta}} _ {\ mathrm {IV}} = (Z'X) ^ {- 1} Z'y = (Z'X) ^ {- 1} Z'X \ beta + (Z'X) ^ {- 1} Z'e \ rightarrow \ beta}

Mientras $${\ displaystyle Z'e = 0}En el proceso subyacente que genera los datos, el uso apropiado del estimador IV identificará este parámetro. Esto funciona porque IV resuelve para el parámetro único que satisface$${\ displaystyle Z'e = 0}y, por lo tanto, se enfoca en el verdadero parámetro subyacente a medida que aumenta el tamaño de la muestra.

Ahora una extensión: supongamos que hay más instrumentos que los que hay covariables en la ecuación de interés, por lo que Z es un T × M matriz con M> K . Esto a menudo se llama el caso sobre-identificado . En este caso, se puede utilizar el método generalizado de momentos (GMM). El estimador GMM IV es

$${\ displaystyle {\ widehat {\ beta}} _ {\ mathrm {GMM}} = (X'P_ {Z} X) ^ {- 1} X'P_ {Z} y,}

dónde $${\ displaystyle P_ {Z}}se refiere a la matriz de proyección $${\ displaystyle P_ {Z} = Z (Z'Z) ^ {- 1} Z '}.

Tenga en cuenta que esta expresión se colapsa a la primera cuando el número de instrumentos es igual al número de covariables en la ecuación de interés. El IV sobre-identificado es por lo tanto una generalización del IV recién identificado.

esconder

Prueba de que β _{GMM se} colapsa a β _IV en el caso recién identificado

Desarrollando el $${\ displaystyle \ beta _ {GMM}} expresión:

$${\ displaystyle {\ widehat {\ beta}} _ {\ mathrm {GMM}} = (X ^ {\ mathrm {T}} Z (Z ^ {\ mathrm {T}} Z) ^ {- 1} Z ^ {\ mathrm {T}} X) ^ {- 1} X ^ {\ mathrm {T}} Z (Z ^ {\ mathrm {T}} Z) ^ {- 1} Z ^ {\ mathrm {T}} y}

En el caso que acabamos identificado, tenemos el mayor número de instrumentos como covariables, de manera que la dimensión de X es el mismo que el de  Z . Por lo tanto,$${\ displaystyle X ^ {\ mathrm {T}} Z, Z ^ {\ mathrm {T}} Z} y $${\ displaystyle Z ^ {\ mathrm {T}} X}Son todas matrices cuadradas de la misma dimensión. Podemos ampliar la inversa, utilizando el hecho de que, para cualquier invertible n -by- n matrices A y B , ( AB ) ^-1 = B ^-1 A ^-1 (ver matriz # Propiedades invertibles ):

{\ displaystyle {\ begin {alineado} {\ widehat {\ beta}} _ {\ mathrm {GMM}} & = (Z ^ {\ mathrm {T}} X) ^ {- 1} (Z ^ {\ mathrm {T}} Z) (X ^ {\ mathrm {T}} Z) ^ {- 1} X ^ {\ mathrm {T}} Z (Z ^ {\ mathrm {T}} Z) ^ {- 1} Z ^ {\ mathrm {T}} y \\ & = (Z ^ {\ mathrm {T}} X) ^ {- 1} (Z ^ {\ mathrm {T}} Z) (Z ^ {\ mathrm { T}} Z) ^ {- 1} Z ^ {\ mathrm {T}} y \\ & = (Z ^ {\ mathrm {T}} X) ^ {- 1} Z ^ {\ mathrm {T}} y \\ & = {\ widehat {\ beta}} _ {\ mathrm {IV}} \ end {alineado}}}

Referencia: ver Davidson y Mackinnnon (1993) ^[13] : 218

Tenga en cuenta que hay un estimador de identificación insuficiente equivalente para el caso donde m  . Dado que los parámetros son las soluciones para un conjunto de ecuaciones lineales, un modelo subidentificado que utiliza el conjunto de ecuaciones$${\ displaystyle Z'v = 0} No tiene una solución única.

La interpretación como mínimos cuadrados de dos etapas [ editar ]

Un método computacional que se puede usar para calcular las estimaciones IV es los mínimos cuadrados de dos etapas (2SLS o TSLS). En la primera etapa, cada variable explicativa que es una covariada endógena en la ecuación de interés se restaura en todas las variables exógenas en el modelo, incluidas ambas covariables exógenas en la ecuación de interés y los instrumentos excluidos. Se obtienen los valores predichos de estas regresiones:

Etapa 1: Regresa cada columna de X en Z , ($${\ displaystyle X = Z \ delta + {\ text {errores}}}):

$${\ displaystyle {\ widehat {\ delta}} = (Z ^ {\ mathrm {T}} Z) ^ {- 1} Z ^ {\ mathrm {T}} X, \,}

y guarda los valores predichos:

$${\ displaystyle {\ widehat {X}} = Z {\ widehat {\ delta}} = {\ color {ProcessBlue} Z (Z ^ {\ mathrm {T}} Z) ^ {- 1} Z ^ {\ mathrm {T}}} X = {\ color {ProcessBlue} P_ {Z}} X. \,}

En la segunda etapa, la regresión del interés se estima como de costumbre, excepto que en esta etapa cada covariable endógeno se reemplaza con los valores predichos de la primera etapa:

Etapa 2: Regresa Y en los valores predichos de la primera etapa:

$${\ displaystyle Y = {\ widehat {X}} \ beta + \ mathrm {noise}, \,}

lo que da

$${\ displaystyle \ beta _ {2SLS} = \ left (X ^ {\ mathrm {T}} {\ color {ProcessBlue} P_ {Z}} X \ right) ^ {- 1} X ^ {\ mathrm {T} } {\ color {ProcessBlue} P_ {Z}} Y.}

esconder

Prueba: cálculo del estimador 2SLS

Tenga en cuenta que el estimador habitual de OLS es: $${\ displaystyle ({\ widehat {X}} ^ {\ mathrm {T}} {\ widehat {X}}) ^ {- 1} {\ widehat {X}} ^ {\ mathrm {T}} Y}. Reemplazo$${\ displaystyle {\ widehat {X}} = P_ {Z} X} y notando que $${\ displaystyle P_ {Z}}Es una matriz simétrica e idempotente , por lo que$${\ displaystyle P_ {Z} ^ {\ mathrm {T}} P_ {Z} = P_ {Z} P_ {Z} = P_ {Z}}

$${\ displaystyle \ beta _ {2SLS} = ({\ widehat {X}} ^ {\ mathrm {T}} {\ widehat {X}}) ^ {- 1} {\ widehat {X}} ^ {\ mathrm {T}} Y = \ izquierda (X ^ {\ mathrm {T}} P_ {Z} ^ {\ mathrm {T}} P_ {Z} X \ derecha) ^ {- 1} X ^ {\ mathrm {T }} P_ {Z} ^ {\ mathrm {T}} Y = \ left (X ^ {\ mathrm {T}} P_ {Z} X \ right) ^ {- 1} X ^ {\ mathrm {T}} P_ {Z} Y.}

El estimador resultante de $${\ displaystyle \ beta}es numéricamente idéntico a la expresión que se muestra arriba. Se debe hacer una pequeña corrección a los residuales de la suma de cuadrados en el modelo ajustado de la segunda etapa para que la matriz de covarianza de$${\ displaystyle \ beta} se calcula correctamente

No paramétrico de análisis [ editar ]

Cuando la forma de las ecuaciones estructurales es desconocida, una variable instrumental $${\ displaystyle Z} Todavía se puede definir a través de las ecuaciones:

$${\ displaystyle x = g (z, u) \,}

$${\ displaystyle y = f (x, u) \,}

dónde $${\ displaystyle f} y $${\ displaystyle g} Son dos funciones arbitrarias y $${\ displaystyle Z} es independiente de $${\ displaystyle U}. A diferencia de los modelos lineales, sin embargo, las mediciones de$${\ displaystyle Z, X} y $${\ displaystyle Y} No permiten la identificación del efecto causal promedio de $${\ displaystyle X} en $${\ displaystyle Y}, denotado ACE

$${\ displaystyle {\ text {ACE}} = \ Pr (y \ mid {\ text {do}} (x)) = \ operatorname {E} _ {u} [f (x, u)].}

Balke y Pearl [1997] obtuvieron límites estrictos en ACE y demostraron que pueden proporcionar información valiosa sobre el signo y el tamaño de ACE. ^[14]

En el análisis lineal, no hay pruebas para falsificar el supuesto de que $${\ displaystyle Z} es instrumental en relación con la pareja $${\ displaystyle (X, Y)}. Este no es el caso cuando$${\ displaystyle X}es discreto Perla (2000) ha demostrado que, para todos$${\ displaystyle f} y $${\ displaystyle g}, la siguiente restricción, llamada "Desigualdad instrumental" debe mantenerse siempre que $${\ displaystyle Z}satisface las dos ecuaciones anteriores: ^[9]

$${\ displaystyle \ max _ {x} \ sum _ {y} [\ max _ {z} \ Pr (y, x \ mid z)] \ leq 1.}

En la interpretación de las estimaciones IV [ editar ]

La exposición anterior supone que el efecto causal del interés no varía según las observaciones, es decir, que $${\ displaystyle \ beta}es una constante Generalmente, diferentes sujetos responderán de diferentes maneras a los cambios en el "tratamiento" x . Cuando se reconoce esta posibilidad, el efecto promedio en la población de un cambio en x en ypuede diferir del efecto en una subpoblación dada. Por ejemplo, el efecto promedio de un programa de capacitación laboral puede diferir sustancialmente entre el grupo de personas que realmente reciben la capacitación y el grupo que elige no recibir capacitación. Por estas razones, los métodos IV invocan suposiciones implícitas sobre la respuesta conductual, o, más generalmente, suposiciones sobre la correlación entre la respuesta al tratamiento y la propensión a recibir tratamiento. ^[15]

El estimador estándar IV puede recuperar los efectos del tratamiento promedio local (TARDE) en lugar de los efectos del tratamiento promedio (ATE). ^[1] Imbens y Angrist (1994) demuestran que la estimación lineal IV puede interpretarse en condiciones débiles como un promedio ponderado de los efectos del tratamiento promedio local, donde los pesos dependen de la elasticidad del regresor endógeno a los cambios en las variables instrumentales. En términos generales, eso significa que el efecto de una variable solo se revela para las subpoblaciones afectadas por los cambios observados en los instrumentos, y que las subpoblaciones que responden más a los cambios en los instrumentos tendrán los mayores efectos en la magnitud de la estimación IV.

Por ejemplo, si un investigador utiliza la presencia de una universidad de concesión de tierras como un instrumento para la educación universitaria en una regresión de ganancias, ella identifica el efecto de la universidad en las ganancias de la subpoblación que obtendría un título universitario si una universidad está presente pero que no obtener un título si una universidad no está presente. Este enfoque empírico, sin más suposiciones, no le dice al investigador nada sobre el efecto de la universidad entre las personas que siempre o nunca obtendrían un título universitario, independientemente de si existe una universidad local.

Los problemas potenciales [ editar ]

Las estimaciones de las variables instrumentales son generalmente inconsistentes si los instrumentos están correlacionados con el término de error en la ecuación de interés. Como señalan Bound, Jaeger y Baker (1995), otro problema es causado por la selección de instrumentos "débiles", que son malos predictores del predictor de pregunta endógeno en la ecuación de la primera etapa. ^[16] En este caso, la predicción de la pregunta predictor por el instrumento será deficiente y los valores pronosticados tendrán muy poca variación. En consecuencia, es poco probable que tengan mucho éxito en la predicción del resultado final cuando se usan para reemplazar el predictor de la pregunta en la ecuación de la segunda etapa.

En el contexto del ejemplo de fumar y salud mencionado anteriormente, los impuestos al tabaco son instrumentos débiles para fumar si el estado de fumar no responde en gran medida a los cambios en los impuestos. Si los impuestos más altos no inducen a las personas a dejar de fumar (o no comienzan a fumar), entonces la variación en las tasas impositivas no nos dice nada sobre el efecto del hábito de fumar en la salud. Si los impuestos afectan la salud a través de otros canales además de su efecto sobre el hábito de fumar, entonces los instrumentos son inválidos y el enfoque de las variables instrumentales puede producir resultados engañosos. Por ejemplo, los lugares y las épocas con poblaciones relativamente preocupadas por la salud pueden implementar altos impuestos al tabaco y exhibir una mejor salud, incluso manteniendo constantes las tasas de consumo de tabaco, por lo que observaríamos una correlación entre los impuestos sobre la salud y el tabaco, incluso si el hecho de fumar no tuviera efecto. en salud. En este caso,

Las propiedades y la prueba de hipótesis de muestreo [ editar ]

Cuando las covariables son exógenas, las propiedades de muestra pequeña del estimador OLS se pueden derivar de una manera directa mediante el cálculo de los momentos del estimador condicional en X. Cuando algunas de las covariables son endógenas, de modo que se implementa la estimación de variables instrumentales, no se pueden obtener expresiones simples para los momentos del estimador. En general, los estimadores de variables instrumentales solo tienen propiedades asintóticas, no finitas, deseables, y la inferencia se basa en aproximaciones asintóticas a la distribución muestral del estimador. Incluso cuando los instrumentos no están correlacionados con el error en la ecuación de interés y cuando los instrumentos no son débiles, las propiedades de la muestra finita del estimador de variables instrumentales pueden ser deficientes. Por ejemplo, los modelos exactamente identificados producen estimadores de muestra finitos sin momentos, por lo que se puede decir que el estimador no está ni sesgado ni imparcial, el tamaño nominal de las estadísticas de prueba puede estar sustancialmente distorsionado,^[17]

Ensayo de la rigidez del instrumento y sobreidentificación restricciones [ editar ]

La fuerza de los instrumentos se puede evaluar directamente porque tanto las covariables endógenas como los instrumentos son observables. ^[18] Una regla general para los modelos con un regresor endógeno es: la estadística F contra la nula que los instrumentos excluidos son irrelevantes en la regresión de la primera etapa debe ser mayor que 10.

El supuesto de que los instrumentos no están correlacionados con el término de error en la ecuación de interés no es verificable en modelos identificados exactamente. Si el modelo está sobre identificado, hay información disponible que se puede usar para probar este supuesto. La prueba más común de estas restricciones de identificación excesiva , llamada prueba de Sargan-Hansen , se basa en la observación de que los residuos no deben estar correlacionados con el conjunto de variables exógenas si los instrumentos son realmente exógenos. ^[19] El estadístico de prueba de Sargan-Hansen se puede calcular como$${\ displaystyle TR ^ {2}}(el número de observaciones multiplicado por el coeficiente de determinación ) desde la regresión OLS de los residuos hasta el conjunto de variables exógenas. Esta estadística será asintóticamente chi-cuadrada con m  -  k grados de libertad bajo el nulo de que el término de error no está correlacionado con los instrumentos.

Aplicación a aleatorio y modelos de efectos fijos [ editar ]

En los modelos de efectos aleatorios estándar (RE) y efectos fijos (FE) para datos de panel , se supone que las variables independientes no están correlacionadas con los términos de error. Siempre que haya disponibilidad de instrumentos válidos, los métodos RE y FE se extienden al caso donde algunas de las variables explicativas pueden ser endógenas. Al igual que en la configuración exógena, el modelo RE con variables instrumentales (REIV) requiere supuestos más estrictos que el modelo FE con variables instrumentales (FEIV), pero tiende a ser más eficiente en las condiciones apropiadas. ^[20]

Para arreglar ideas, considera el siguiente modelo:

$${\ displaystyle y_ {it} = x_ {it} \ beta + c_ {i} + u_ {it}}

dónde $${\ displaystyle c_ {i}} es un efecto invariante en el tiempo específico de la unidad no observado (llámelo efecto no observado) y $${\ displaystyle x_ {it}} se puede correlacionar con $${\ displaystyle u_ {is}}para s posiblemente diferente de t . Supongamos que existe un conjunto de instrumentos válidos.$${\ displaystyle z_ {i} = (z_ {i1}, \ ldots, z_ {it})}.

En la configuración REIV, las suposiciones clave incluyen que $${\ displaystyle z_ {i}} no está correlacionado con $${\ displaystyle c_ {i}} tanto como $${\ displaystyle u_ {it}}para $${\ displaystyle t = 1, \ ldots, T}. De hecho, para que el estimador REIV sea eficiente, se requieren condiciones más fuertes que la falta de correlación entre los instrumentos y el efecto no observado.

Por otro lado, el estimador de FEIV solo requiere que los instrumentos sean exógenos con términos de error después de condicionar el efecto no observado, es decir, $${\ displaystyle E [u_ {it} \ mid z_ {i}, c_ {i}] = 0 [1]}. ^[20] La condición FEIV permite una correlación arbitraria entre los instrumentos y el efecto no observado. Sin embargo, esta generalidad no es gratuita: no se permiten variables explicativas e instrumentales invariantes en el tiempo. Al igual que en el método habitual de FE, el estimador utiliza variables degradadas en el tiempo para eliminar el efecto no observado. Por lo tanto, el estimador FEIV sería de uso limitado si las variables de interés incluyan variables invariables en el tiempo.

La discusión anterior tiene un paralelo con el caso exógeno de los modelos RE y FE. En el caso exógeno, RE asume una falta de correlación entre las variables explicativas y el efecto no observado, y la FE permite una correlación arbitraria entre las dos. Al igual que en el caso estándar, REIV tiende a ser más eficiente que el FEIV siempre que se cumplan las suposiciones adecuadas.