ARTÍCULOS DE ESTADÍSTICA

Los modelos de ecuaciones simultáneas son un tipo de modelo estadístico en forma de un conjunto de ecuaciones simultáneas lineales . Se utilizan a menudo en econometría . Uno puede estimar estos modelos ecuación por ecuación; sin embargo, los métodos de estimación que explotan el sistema de ecuaciones, como el método generalizado de momentos (GMM) y la estimación de variables instrumentales (IV), tienden a ser más eficientes . 

Forma estructural y reducida [ editar ]

Supongamos que hay m ecuaciones de regresión de la forma

$${\ displaystyle y_ {it} = y _ {- i, t} '\ gamma _ {i} + x_ {it}' \; \! \ beta _ {i} + u_ {it}, \ quad i = 1, \ ldots, m,}

donde i es el número de la ecuación, y t = 1, ..., T es el índice de observación. En estas ecuaciones x _que es la k _i× 1 vector de variables exógenas, y _que es la variable dependiente, y _{-i, t} es el n _i × 1 vector de todas las demás variables endógenas que entran en el i ^ésimo ecuación en la derecha lado, y T _es son los términos de error. La notación “- i ” indica que el vector y _{−i, t} puede contener cualquiera de los y's a excepción de y _que (puesto que ya está presente en el lado izquierdo). Los coeficientes de regresión β _i y γ _i son de dimensiones k _i × 1 y n _i × 1 correspondientemente. Verticalmente apilado de las T observaciones correspondientes a la i ^º ecuación, podemos escribir cada ecuación en forma vectorial como

$${\ displaystyle y_ {i} = Y _ {- i} \ gamma _ {i} + X_ {i} \ beta _ {i} + u_ {i}, \ quad i = 1, \ ldots, m,}

donde Y _i y u _i son T × 1 vectores, X _i es un T × k _i matriz de regresores exógenos, y Y _-i es un T × n _i matriz de regresores endógenos en el lado derecho de la i ^º ecuación . Finalmente, podemos mover todas las variables endógenas hacia el lado izquierdo y escribir las ecuaciones m conjuntamente en forma vectorial como

$${\ displaystyle Y \ Gamma = X \ mathrm {B} + U. \,}

Esta representación se conoce como la forma estructural . En esta ecuación Y = [ y ₁ y ₂ ... y _m ] es la matriz de variables dependientes T × m . Cada una de las matrices Y _-i es de hecho un n _i -columned submatriz de esta Y . La matriz m × m Γ, que describe la relación entre las variables dependientes, tiene una estructura complicada. Tiene unos en la diagonal, y todos los demás elementos de cada columna i son los componentes del vector −γ _io ceros, dependiendo de qué columnas de Y se incluyeron en la matriz Y _−i . La matriz X de T × k contiene todos los regresores exógenos de todas las ecuaciones, pero sin repeticiones (es decir, la matriz X debe ser de rango completo). Así, cada X _i es un k _i -columned submatriz de X . La matriz Β tiene un tamaño k × m , y cada una de sus columnas consta de los componentes de los vectores β _i y los ceros, según cuál de los regresores de X se incluyó o excluyó de X _i . Por último, u= [ u ₁ u ₂ ... u _m ] es una matriz T × m de los términos de error.

Después de multiplicar la ecuación estructural por Γ ⁻¹ , el sistema puede escribirse en forma reducida como

$${\ displaystyle Y = X \ mathrm {B} \ Gamma ^ {- 1} + U \ Gamma ^ {- 1} = X \ Pi + V. \,}

Este ya es un modelo lineal general simple , y puede estimarse, por ejemplo, por mínimos cuadrados ordinarios . Lamentablemente, la tarea de descomponer la matriz estimada.$${\ displaystyle \ scriptstyle {\ hat {\ Pi}}}en los factores individuales Β y Γ ⁻¹ es bastante complicado, y por lo tanto la forma reducida es más adecuada para la predicción pero no para la inferencia.

Suposiciones [ editar ]

En primer lugar, el rango de la matriz X de los regresores exógenos debe ser igual a k , tanto en muestras finitas como en el límite como T → ∞ (este último requisito significa que en el límite la expresión$${\ displaystyle \ scriptstyle {\ frac {1} {T}} X '\! X}debe converger a una matriz kx k no degenerada ). También se supone que la matriz be no es degenerada.

En segundo lugar, se supone que los términos de error son independientes en serie y distribuidos de manera idéntica . Es decir, si la fila t ^th de la matriz U se denota por u _( t ) , entonces la secuencia de los vectores { u _( t ) } debe ser iid, con media cero y alguna matriz de covarianza Σ (lo cual es desconocido). En particular, esto implica que E [ U ] = 0 , y E [ U′U ] = T  Σ .

Por último, las condiciones de identificación requieren que el número de incógnitas en este sistema de ecuaciones no exceda el número de ecuaciones. Más específicamente, la condición de orden requiere que para cada ecuación k _i + n _i ≤ k , que se puede expresar como "el número de variables exógenas excluidas es mayor o igual al número de variables endógenas incluidas". La condición del rango de identificabilidad es ese rango (Π _i 0 ) = n _i , donde Π _i 0 es a ( k - k _i ) × n _i matriz que se obtiene de Π al tachar aquellas columnas que corresponden a las variables endógenas excluidas y aquellas filas que corresponden a las variables exógenas incluidas.

Estimación [ editar ]

Mínimos cuadrados de dos etapas (2SLS) [ editar ]

El método de estimación más simple y más común ^[2] para el modelo de ecuaciones simultáneas es el denominado método de mínimos cuadrados en dos etapas , desarrollado independientemente por Theil (1953) y Basmann (1957) . Es una técnica de ecuación por ecuación, donde los regresores endógenos en el lado derecho de cada ecuación están siendo instrumentados con los regresores X de todas las demás ecuaciones. El método se llama "dos etapas" porque realiza la estimación en dos pasos: ^[3]

Paso 1 : Regresa Y _−i en X y obtén los valores predichos$${\ displaystyle \ scriptstyle {\ hat {Y}} _ {\! - i}};

Paso 2 : estimar γ _i , β _i mediante la regresión de mínimos cuadrados ordinarios de y _i en$${\ displaystyle \ scriptstyle {\ hat {Y}} _ {\! - i}}y X _i .

Si el i ^ª ecuación en el modelo se escribe como

{\ displaystyle y_ {i} = {\ begin {pmatrix} Y _ {- i} & X_ {i} \ end {pmatrix}} {\ begin {pmatrix} \ gamma _ {i} \\\ beta _ {i} \ fin {pmatrix}} + u_ {i} \ equiv Z_ {i} \ delta _ {i} + u_ {i},}

donde Z _i es un T × ( n _i  + k _i ) matriz de ambos regresores endógenos y exógenos en el i ^ésimo ecuación, y δ _i es un ( n _i  + k _i ) vectores -dimensional de coeficientes de regresión, entonces el estimador MC2E de δ se _me dará por ^[3]

$${\ displaystyle {\ hat {\ delta}} _ {i} = {\ big (} {\ hat {Z}} '_ {i} {\ hat {Z}} _ {i} {\ big)} ^ {-1} {\ hat {Z}} '_ {i} y_ {i} = {\ big (} Z' _ {i} PZ_ {i} {\ big)} ^ {- 1} Z '_ { i} Py_ {i},}

donde P = X  ( X  ' X ) ^-1 X  ' es la matriz de proyección sobre el espacio lineal abarcado por los regresores exógenos X .

Mínimos cuadrados indirectos [ editar ]

Mínimos cuadrados indirectos es un enfoque en econometría donde los coeficientes en un modelo de ecuaciones simultáneas se estiman a partir del modelo de forma reducida utilizando mínimos cuadrados ordinarios . ^[4] [5]Para esto, el sistema estructural de ecuaciones se transforma primero en la forma reducida. Una vez que se estiman los coeficientes, el modelo vuelve a la forma estructural.

Máxima verosimilitud de información limitada (LIML) [ editar ]

El método de máxima verosimilitud de "información limitada" se sugirió a MA Girshick en 1947, ^[6] y fue formalizado por TW Anderson y H. Rubin en 1949. ^[7] Se usa cuando uno está interesado en estimar una sola ecuación estructural a la vez ( de ahí su nombre de información limitada), digamos para observación i:

$${\ displaystyle y_ {i} = Y _ {- i} \ gamma _ {i} + X_ {i} \ beta _ {i} + u_ {i} \ equiv Z_ {i} \ delta _ {i} + u_ { yo}}

Las ecuaciones estructurales para las restantes variables endógenas Y _−i no están especificadas, y se dan en su forma reducida:

$${\ displaystyle Y _ {- i} = X \ Pi + U _ {- i}}

La notación en este contexto es diferente a la del caso IV simple . Uno tiene:

• $${\ displaystyle Y _ {- i}}: La (s) variable (s) endógena (s).
• $${\ displaystyle X _ {- i}}: La (s) variable (s) exógena (s)
• $${\ displaystyle X}: El instrumento (s) (a menudo denotado) $${\ displaystyle Z})

La fórmula explícita para el LIML es: ^[8]

$${\ displaystyle {\ hat {\ delta}} _ {i} = {\ Big (} Z '_ {i} (I- \ lambda M) Z_ {i} {\ Big)} ^ {\! - 1} Z '_ {i} (I- \ lambda M) y_ {i},}

donde M = I - X  ( X  ′ X ) ⁻¹ X  ′ , y λ es la raíz característica más pequeña de la matriz:

{\ displaystyle {\ Big (} {\ begin {bmatrix} y_ {i} \\ Y _ {- i} \ end {bmatrix}} M_ {i} {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix}} {\ Big)} {\ Big (} {\ begin {bmatrix} y_ {i} \\ Y _ {- i} \ end {bmatrix}} M {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix}} {\ Big)} ^ {\! - 1}}

donde, de manera similar, M _i = I - X _i  ( X _i ′ X _i ) ⁻¹ X _i ′ .

En otras palabras, λ es la solución más pequeña del problema del valor propio generalizado , ver Theil (1971 , p. 503):

{\ displaystyle {\ Big |} {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix}} 'M_ {i} {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix}} - \ lambda {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix}} 'M {\ begin {bmatrix} y_ {i} & Y _ {- i} \ end {bmatrix }} {\ Big |} = 0}

Estimadores de la clase K [ editar ]

El LIML es un caso especial de los estimadores de clase K: ^[9]

$${\ displaystyle {\ hat {\ delta}} = {\ Big (} Z '(I- \ kappa M) Z {\ Big)} ^ {\! - 1} Z' (I- \ kappa M) y, }

con:

• {\ displaystyle \ delta = {\ begin {bmatrix} \ beta _ {i} & \ gamma _ {i} \ end {bmatrix}}}
• {\ displaystyle Z = {\ begin {bmatrix} X_ {i} & Y _ {- i} \ end {bmatrix}}}

Varios estimadores pertenecen a esta clase:

• κ = 0: OLS
• κ = 1: 2SLS. Tenga en cuenta que en este caso,$${\ displaystyle I- \ kappa M = IM = P} La matriz de proyección habitual del 2SLS.
• κ = λ: LIML
• κ = λ - α (nK): estimador de Fuller (1977) . Aquí, K representa el número de instrumentos, n el tamaño de la muestra y α es una constante positiva para especificar. Un valor de α = 1 producirá un estimador que es aproximadamente imparcial. ^[10]

Mínimos cuadrados de tres etapas (3SLS) [ editar ]

El estimador de mínimos cuadrados de tres etapas fue introducido por Zellner y Theil (1962) . ^[11] Se puede ver como un caso especial de GMM de múltiples ecuaciones donde el conjunto de variables instrumentales es común a todas las ecuaciones. ^[12] Si todos los regresores están predeterminados, 3SLS se reduce a regresiones aparentemente no relacionadas (SUR). Por lo tanto, también puede verse como una combinación de mínimos cuadrados de dos etapas (2SLS) con SUR.

Uso de restricciones de ecuaciones cruzadas para lograr la identificación [ editar ]

En los modelos de ecuaciones simultáneas, el método más común para lograr la identificación es imponer restricciones de parámetros dentro de la ecuación. ^[13] Sin embargo, la identificación también es posible mediante restricciones de ecuaciones cruzadas.

Para ilustrar cómo se pueden usar las restricciones de ecuaciones cruzadas para la identificación, considere el siguiente ejemplo de Wooldridge ^[13]

                              y ₁ = γ ₁₂ y ₂ + δ ₁₁ z ₁ + δ ₁₂ z ₂ + δ ₁₃ z ₃ + u ₁
                                        y ₂ = γ ₂₁ y ₁ + δ ₂₁ z ₁ + δ ₂₂ z ₂ + u ₂

donde z's no están correlacionados con u's y y's son variables endógenas . Sin más restricciones, la primera ecuación no se identifica porque no hay una variable exógena excluida. La segunda ecuación se identifica solo si δ ₁₃ 0, que se supone que es cierto para el resto de la discusión.

Ahora imponemos la restricción de la ecuación cruzada de δ ₁₂ = δ ₂₂ . Dado que se identifica la segunda ecuación, podemos tratar δ ₁₂ como se conoce con el propósito de identificación. Entonces, la primera ecuación se convierte en:

                              y ₁ - δ ₁₂ z ₂ = γ ₁₂ y ₂ + δ ₁₁ z ₁ + δ ₁₃ z ₃ + u ₁

Luego, podemos usar (z ₁ , z ₂ , z ₃ ) como instrumentos para estimar los coeficientes en la ecuación anterior, ya que hay una variable endógena (y ₂ ) y una variable exógena excluida (z ₂ ) en el lado derecho. Por lo tanto, las restricciones de ecuación cruzada en lugar de las restricciones dentro de la ecuación pueden lograr la identificación.

Aplicaciones en ciencias sociales [ editar ]

En todos los campos y disciplinas, los modelos de ecuaciones simultáneas se aplican a diversos fenómenos observacionales. Estas ecuaciones se aplican cuando se asume que los fenómenos son recíprocamente causales. El ejemplo clásico es la oferta y la demanda en economía . En otras disciplinas hay ejemplos como las evaluaciones de candidatos y la identificación de partidos ^[14] o la opinión pública y la política social en ciencias políticas ; ^[15] [16] inversión vial y demanda de viajes en geografía; ^[17] y el logro educativo y la entrada de la paternidad en sociología o demografía . ^[18]El modelo de ecuación simultánea requiere una teoría de causalidad recíproca que incluya características especiales si los efectos causales se estiman como retroalimentación simultánea en oposición a los 'bloques' unilaterales de una ecuación donde un investigador está interesado en el efecto causal de X en Y mientras se mantiene constante el efecto causal de Y en X, o cuando el investigador sabe la cantidad exacta de tiempo que toma para que tenga lugar cada efecto causal, es decir, la duración de los retrasos causales. En lugar de efectos retardados, la retroalimentación simultánea significa estimar el impacto simultáneo y perpetuo de X e Y entre sí. Esto requiere una teoría de que los efectos causales son simultáneos en el tiempo, o tan complejos que parecen comportarse simultáneamente; Un ejemplo común son los estados de ánimo de los compañeros de cuarto. ^[19]Para estimar modelos de retroalimentación simultánea, también es necesaria una teoría del equilibrio: que X e Y están en estados relativamente estables o son parte de un sistema (sociedad, mercado, aula) que se encuentra en un estado relativamente estable. 

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Para un conjunto de datos aproximadamente normal , los valores dentro de una desviación estándar de la media representan aproximadamente el 68% del conjunto; mientras que dentro de dos desviaciones estándar representan alrededor del 95%; y dentro de tres desviaciones estándar representan alrededor del 99.7%. Los porcentajes mostrados son probabilidades teóricas redondeadas destinadas solo a aproximar los datos empíricos derivados de una población normal. Esta regla generalmente se enseña dentro de las matemáticas básicas comunes.

Intervalo de predicción (en el eje y ) dado desde la puntuación estándar (en el eje x ). El eje y se escala logarítmicamente (pero los valores en él no se modifican).

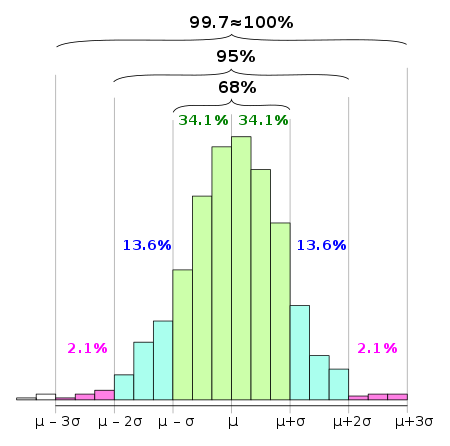
En las estadísticas , la regla 68–95–99.7 , también conocida como regla empírica , es una abreviatura utilizada para recordar el porcentaje de valores que se encuentran dentro de una banda alrededor de la media en una distribución normalcon un ancho de dos, cuatro y seis estándares. desviaciones , respectivamente; con más precisión, 68.27%, 95.45% y 99.73% de los valores se encuentran dentro de una, dos y tres desviaciones estándar de la media, respectivamente.

En notación matemática, estos hechos se pueden expresar de la siguiente manera, donde Χ es una observación de una variable aleatoria normalmente distribuida , μ es la media de la distribución, y σes su desviación estándar:

${\displaystyle {\begin{aligned}\Pr(\mu -1\sigma \leq X\leq \mu +1\sigma )&\approx 0.6827\\\Pr(\mu -2\sigma \leq X\leq \mu +2\sigma )&\approx 0.9545\\\Pr(\mu -3\sigma \leq X\leq \mu +3\sigma )&\approx 0.9973\end{aligned}}}$

En las ciencias empíricas, la así llamada regla de tres sigmaexpresa una heurística convencional de que casi todos los valores se consideran dentro de las tres desviaciones estándar de la media, y por lo tanto es empíricamente útil tratar la probabilidad del 99.7% como una certeza. ^[1] La utilidad de esta heurística depende significativamente de la pregunta en consideración. En las ciencias sociales, un resultado puede considerarse "significativo" si su nivel de confianza es del orden de un efecto de sigma doble (95%), mientras que en la física de partículas , existe una convención de un efecto de sigma cinco (99.99994%). confianza) siendo requeridos para calificar como un descubrimiento .

La "regla de tres sigma" se relaciona con un resultado también conocido como la regla de tres sigma, que establece que incluso para las variables de distribución no normal, al menos el 88.8% de los casos debe estar dentro de intervalos de tres sigma correctamente calculados. Se sigue de la desigualdad de Chebyshev . Para distribuciones unimodales, la probabilidad de estar dentro del intervalo es de al menos el 95%. Puede haber ciertas suposiciones para una distribución que obligue a que esta probabilidad sea al menos del 98%.

Función de distribución acumulativa [ editar ]

Diagrama que muestra la función de distribución acumulada para la distribución normal con media ( μ ) 0 y varianza ( σ ² ) 1.

Estos valores numéricos "68%, 95%, 99,7%" provienen de la función de distribución acumulativa de la distribución normal .

El intervalo de predicción para cualquier puntaje estándar zcorresponde numéricamente a (1− (1− Φ _{μ , σ ²} (z)) · 2).

Por ejemplo, Φ (2) ≈ 0.9772 , o Pr ( X ≤ μ + 2 σ ) ≈ 0.9772 , que corresponde a un intervalo de predicción de (1 - (1 - 0.97725) · 2) = 0.9545 = 95.45%. Tenga en cuenta que este no es un intervalo simétrico, es simplemente la probabilidad de que una observación sea menor que μ + 2 σ . Para calcular la probabilidad de que una observación se encuentre dentro de dos desviaciones estándar de la media (pequeñas diferencias debidas al redondeo):

$${\ displaystyle \ Pr (\ mu -2 \ sigma \ leq X \ leq \ mu +2 \ sigma) = \ Phi (2) - \ Phi (-2) \ approx 0.9772- (1-0.9772) \ approx 0.9545}

Esto está relacionado con el intervalo de confianza utilizado en las estadísticas:$${\ displaystyle {\ bar {X}} \ pm 2 {\ frac {\ sigma} {\ sqrt {n}}}} es aproximadamente un intervalo de confianza del 95% cuando $${\ displaystyle {\ bar {X}}} Es el promedio de una muestra de tamaño. $${\ displaystyle n}.

Pruebas de normalidad [ editar ]

Artículo principal: Prueba de normalidad.

La "regla 68-95-99.7" se usa a menudo para obtener rápidamente una estimación de probabilidad aproximada de algo, dada su desviación estándar, si se supone que la población es normal. También se usa como prueba simple para valores atípicos si la población se supone normal, y como prueba de normalidad si la población es potencialmente no normal.

Para pasar de una muestra a una serie de desviaciones estándar, primero se calcula la desviación , ya sea el error o el residuo, dependiendo de si se conoce la media de la población o solo se estima. El siguiente paso es estandarizar (dividir por la desviación estándar de la población), si se conocen los parámetros de la población, o estudiar (dividir por una estimación de la desviación estándar), si los parámetros son desconocidos y solo se estiman.

Para usarlo como prueba de valores atípicos o de normalidad, se calcula el tamaño de las desviaciones en términos de desviaciones estándar y se compara con la frecuencia esperada. Dado un conjunto de muestras, uno puede calcular los residuos estudiados y compararlos con la frecuencia esperada: los puntos que caen más de 3 desviaciones estándar de la norma son probablemente valores atípicos (a menos que el tamaño de la muestrasea ​​significativamente grande, por lo que se espera una muestra de este extremo), y si hay muchos puntos más de 3 desviaciones estándar de la norma, es probable que haya razones para cuestionar la normalidad asumida de la distribución. Esto se mantiene cada vez más fuerte para movimientos de 4 o más desviaciones estándar.

Uno puede calcular de manera más precisa, aproximando el número de movimientos extremos de una magnitud dada o mayor por una distribución de Poisson , pero simplemente, si uno tiene múltiples 4 movimientos de desviación estándar en una muestra de tamaño 1,000, uno tiene una razón sólida para considerar estos valores atípicos o Cuestionar la normalidad asumida de la distribución.

Por ejemplo, un evento 6 σ corresponde a una probabilidad de aproximadamente dos partes por billón . Por ejemplo, si se considera que los eventos ocurren diariamente, esto correspondería a un evento esperado cada 1.4 millones de años. Esto da una prueba de normalidad simple : si uno es testigo de un 6 σ en datos diarios y ha pasado significativamente menos de 1 millón de años, entonces una distribución normal probablemente no proporcione un buen modelo para la magnitud o la frecuencia de grandes desviaciones a este respecto.

En The Black Swan , Nassim Nicholas Taleb da el ejemplo de los modelos de riesgo según los cuales la caída del Black Monday correspondería a un evento 36- σ : la ocurrencia de tal evento debería sugerir instantáneamente que el modelo es defectuoso, es decir, que el proceso bajo La consideración no está modelada satisfactoriamente por una distribución normal. Los modelos refinados deben considerarse, por ejemplo, mediante la introducción de la volatilidad estocástica . En tales discusiones, es importante estar al tanto del problema de la falacia del jugador , que establece que una sola observación de un evento raro no contradice que el evento es de hecho raro ^{[ cita requerida ]}. Es la observación de una pluralidad de eventos supuestamente raros que socava cada vez más la hipótesis de que son raros, es decir, la validez del modelo asumido. Un modelo adecuado de este proceso de pérdida gradual de confianza en una hipótesis implicaría la designación de probabilidad previa no solo para la hipótesis en sí, sino para todas las hipótesis alternativas posibles. Por esta razón, las pruebas estadísticas de hipótesis no funcionan tanto confirmando una hipótesis que se considere probable, sino refutando hipótesis que se consideran poco probables .

Tabla de valores numéricos [ editar ]

Debido a las colas exponenciales de la distribución normal, las probabilidades de desviaciones más altas disminuyen muy rápidamente. De las reglas para datos normalmente distribuidos para un evento diario:

Distancia	Fracción esperada de la población dentro del rango	Frecuencia aproximada esperada fuera del rango	Frecuencia aproximada para evento diario.
μ ± 0.5σ	0.382 924 922 548 026	2 en 3	Cuatro o cinco veces a la semana.
μ ± σ	0.682 689 492 137 086	1 en 3	Dos veces a la semana
μ ± 1.5σ	0.866 385 597 462 284	1 en 7	Semanal
μ ± 2σ	0.954 499 736 103 642	1 en 22	Cada tres semanas
μ ± 2.5σ	0,987 580 669 348 448	1 en 81	Trimestral
μ ± 3σ	0.997 300 203 936 740	1 en 370	Anual
μ ± 3.5σ	0.999 534 741 841 929	1 en 2149	Cada seis años
μ ± 4σ	0.999 936 657 516 334	1 en 15 787	Cada 43 años (dos veces en la vida)
μ ± 4.5σ	0.999 993 204 653 751	1 en 147 160	Cada 403 años (una vez en la era moderna).
μ ± 5σ	0.999 999 426 696 856	1 en 1 744 278	Cada 4776 años (una vez en la historia registrada)
μ ± 5.5σ	0.999 999 962 020 875	1 en 26 330 254	Cada 72 090 años (tres veces en la historia de la humanidad moderna )
μ ± 6σ	0.999 999 998 026 825	1 en 506 797 346	Cada 1.38 millones de años (dos veces en la historia de la humanidad )
μ ± 6.5σ	0.999 999 999 919 680	1 en 12 450 197 393	Cada 34 millones de años (dos veces desde la extinción de los dinosaurios )
μ ± 7σ	0.999 999 999 997 440	1 en 390 682 215 445	Cada 1.07 mil millones de años (cuatro veces en la historia de la Tierra )
μ ± x σ	$${\ displaystyle \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}	1 en $${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}}	Cada $${\ displaystyle {\ tfrac {1} {1- \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right)}}} dias