ARTÍCULOS DE ESTADÍSTICA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un paseo de borrachos (finito) es un ejemplo de una cadena absorbente de Markov. ^[1]

En la teoría matemática de la probabilidad , una cadena de Markov absorbente es una cadena de Markov en la que cada estado puede alcanzar un estado de absorción. Un estado absorbente es un estado que, una vez ingresado, no se puede dejar.

Al igual que las cadenas de Markov generales, puede haber cadenas de Markov absorbentes en un tiempo continuo con un espacio de estado infinito. Sin embargo, este artículo se concentra en el caso del espacio de estado discreto de tiempo discreto.

Definición formal [ editar ]

Una cadena de Markov es una cadena absorbente si ^[1] [2]

1. Hay al menos un estado absorbente y
2. es posible pasar de cualquier estado a al menos un estado absorbente en un número finito de pasos.

En una cadena de Markov absorbente, un estado que no absorbe se llama transitorio.

Forma canónica [ editar ]

Deje que una cadena de Markov absorbente con matriz de transición P tenga t estados transitorios y r estado de absorción. Entonces

{\ displaystyle P = \ left ({\ begin {array} {cc} Q&R \\\ mathbf {0} & I_ {r} \ end {array}} \ right),}

donde Q es un t -by- t matriz, R es un no nulo t -by- r matriz, 0 es un r -by- t matriz cero, y I _r es el r -by- r matriz identidad. Por lo tanto, Q describe la probabilidad de transición de algún estado transitorio a otro, mientras que Rdescribe la probabilidad de transición de algún estado transitorio a algún estado absorbente.

Matriz fundamental [ editar ]

Una propiedad básica sobre una cadena de Markov absorbente es el número esperado de visitas a un estado transitorio j a partir de un estado transitorio i (antes de ser absorbido). La probabilidad de realizar la transición de i a j en exactamente k pasos es la entrada ( i , j ) de Q ^k . Resumiendo esto para todos k (de 0 a ∞) produce la matriz fundamental, denotada por N . Se puede probar que

$${\ displaystyle N = \ sum _ {k = 0} ^ {\ infty} Q ^ {k} = (I_ {t} -Q) ^ {- 1},}

donde I _t es la matriz de identidad t- by- t . La entrada ( i ,  j ) de la matriz N es el número esperado de veces que la cadena está en el estado j , dado que la cadena comenzó en el estado i . Con la matriz N en la mano, otras propiedades de la cadena de Markov son fáciles de obtener. ^[2]

Variación en el número de visitas [ editar ]

La varianza en el número de visitas a un estado transitorio j que comienza en un estado transitorio i (antes de ser absorbido) es la entrada ( i , j ) de la matriz

$${\ displaystyle N_ {2} = N (2N _ {\ operatorname {dg}} -I_ {t}) - N _ {\ operatorname {sq}},}

donde N _dg es la matriz diagonal con la misma diagonal que N y N _sq es el producto de Hadamard de N consigo mismo (es decir, cada entrada de N es cuadrada).

Número esperado de pasos [ editar ]

El número esperado de pasos antes de ser absorbido cuando se inicia en el estado transitorio i es la entrada i th del vector

$${\ displaystyle \ mathbf {t} = N \ mathbf {1},}

donde 1 es un vector de columna de longitud- t cuyas entradas son todas 1.

Variación en el número de pasos [ editar ]

La variación en el número de pasos antes de ser absorbida cuando se inicia en el estado transitorio i es la entrada i th del vector

$${\ displaystyle (2N-I_ {t}) \ mathbf {t} - \ mathbf {t} _ {\ operatorname {sq}},}

donde t _sq es el producto de Hadamard de t consigo mismo (es decir, cada entrada de t es cuadrada).

Probabilidades transitorios [ editar ]

La probabilidad de visitar el estado transitorio j cuando se inicia en un estado transitorio i es la entrada ( i , j ) de la matriz

$${\ displaystyle H = (N-I_ {t}) N _ {\ operatorname {dg}} ^ {- 1}.}

Probabilidades de absorción [ editar ]

Otra propiedad es la probabilidad de ser absorbido en el estado de absorción j al comenzar desde el estado transitorio i , que es la entrada ( i , j ) de la matriz.

$${\ displaystyle B = NR.}

Ejemplos [ editar ]

Generación cadena [ editar ]

Artículo principal: Generación de cuerdas.

Considere el proceso de lanzar repetidamente una moneda justa hasta que aparezca la secuencia (cabezas, colas, cabezas). Este proceso está modelado por una cadena de Markov absorbente con matriz de transición.

{\ displaystyle P = {\ begin {bmatrix} 1/2 & 1/2 & 0 & 0 \\ 0 & 1/2 & 1/2 & 0 \\ 1/2 & 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \ end {bmatrix}}.

El primer estado representa la cadena vacía , el segundo estado la cadena "H", el tercer estado la cadena "HT" y el cuarto estado la cadena "HTH". Aunque en realidad, los lanzamientos de monedas cesan después de que se genera la cadena "HTH", la perspectiva de la cadena de Markov absorbente es que el proceso ha pasado al estado de absorción que representa la cadena "HTH" y, por lo tanto, no se puede abandonar.

Para esta cadena de Markov absorbente, la matriz fundamental es

{\ displaystyle {\ begin {alineado} N & = (IQ) ^ {- 1} = \ left ({\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}} - {\ begin {bmatrix} 1 / 2 & 1/2 & 0 \\ 0 & 1/2 & 1/2 \\ 1/2 & 0 & 0 \ end {bmatrix}} \ right) ^ {- 1} \\ [4pt] & = {\ begin {bmatrix} 1/2 & -1 / 2 & 0 \\ 0 & 1/2 & -1 / 2 \\ - 1/2 & 0 & 1 \ end {bmatrix}} ^ {- 1} = {\ begin {bmatrix} 4 & 4 & 2 \\ 2 & 4 & 2 \\ 2 & 2 & 2 \ end {bmatrix}}. \ End { alineado}}}

El número esperado de pasos a partir de cada uno de los estados transitorios es

{\ displaystyle \ mathbf {t} = N \ mathbf {1} = {\ begin {bmatrix} 4 & 4 & 2 \\ 2 & 4 & 2 \\ 2 & 2 & 2 \ end {bmatrix}} {\ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix}} = {\ begin {bmatrix} 10 \\ 8 \\ 6 \ end {bmatrix}}.

Por lo tanto, el número esperado de tiradas de monedas antes de observar la secuencia (cabezas, colas, cabezas) es 10, la entrada para el estado que representa la cadena vacía.

La probabilidad acumulada de terminar un juego de Serpientes y Escaleras por turno  N

Juegos de azar [ editar ]

Los juegos basados ​​totalmente en el azar pueden ser modelados por una cadena absorbente de Markov. Un ejemplo clásico de esto es el antiguo juego de mesa indio Serpientes y escaleras . La gráfica de la derecha ^[3] traza la masa de probabilidad en el estado de absorción única que representa el cuadrado final a medida que la matriz de transición se eleva a potencias cada vez más grandes. Para determinar el número esperado de turnos para completar el juego, calcula el vector t como se describe anteriormente y examina t _inicio , que es aproximadamente 39.2.

Clínica de enfermedades infecciosas [ editar ]

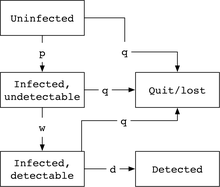
El ejemplo de la prueba de enfermedades infecciosas, ya sea en productos sanguíneos o en clínicas médicas, a menudo se enseña como un ejemplo de una cadena de Markov absorbente. ^[4] El modelo público de los Centros para el Control y la Prevención de Enfermedades (CDC, por sus siglas en inglés) de los EE. UU. Para el VIH y la hepatitis B, por ejemplo, ^[5] ilustra la propiedad de que la absorción de las cadenas de Markov puede conducir a la detección de la enfermedad, frente a la pérdida de la detección a través de otros medios.

En el modelo CDC estándar, la cadena de Markov tiene cinco estados, un estado en el que el individuo no está infectado, luego un estado con virus infectados pero no detectables, un estado con virus detectables y estados absorbentes de haber abandonado / perdido la clínica, o de haber sido detectado (la meta). Las tasas típicas de transición entre los estados de Markov son la probabilidad p por unidad de tiempo de infección con el virus, wpara la tasa de eliminación del período de ventana (tiempo hasta que el virus es detectable), q para la tasa de abandono / pérdida del sistema, y d para detección, asumiendo una tasa típica$${\ displaystyle \ lambda}en el que el sistema de salud administra pruebas del producto sanguíneo o de los pacientes en cuestión.

Ejemplo clásico de detección de virus de VIH o hepatitis.

Se deduce que podemos "seguir" el modelo de Markov para identificar la probabilidad general de detección para una persona que comienza como no detectada, multiplicando las probabilidades de transición a cada estado siguiente del modelo como:

$${\ displaystyle {\ frac {p} {(p + q)}} {\ frac {w} {(w + q)}} {\ frac {d} {(d + q)}}}.

El número absoluto total posterior de pruebas falsas negativas, la preocupación principal de los CDC, se multiplicaría por la probabilidad de alcanzar el estado infectado pero no detectable, multiplicado por la duración de permanecer en el estado indetectable infectado:

$${\ displaystyle {\ frac {p} {(p + q)}} {\ frac {1} {(w + q)}} \ lambda}.

estadística , la desviación es una medida de la diferencia entre el valor observado de una variable y algún otro valor, a menudo la media de esa variable . El signo de la desviación informa la dirección de esa diferencia (la desviación es positiva cuando el valor observado excede el valor de referencia). La magnitud del valor indica el tamaño de la diferencia.

Tipos [ editar ]

Artículo principal: Errores y residuos.

Una desviación que es una diferencia entre un valor observado y el valor verdadero de una cantidad de interés (como la media de una población) es un error y una desviación que es la diferencia entre el valor observado y una estimación del valor verdadero (por ejemplo, la estimación puede ser una media muestral) es un residual . Estos conceptos son aplicables para los datos en los niveles de medición de intervalo e índice .

Desviación sin firma o absoluta [ editar ]

Ver también: Desviación absoluta media y Desviación absoluta mínima.

En estadística , la desviación absoluta de un elemento de un conjunto de datos es la diferencia absoluta entre ese elemento y un punto dado. Normalmente, la desviación se calcula a partir del valor central , y se interpreta como algún tipo de promedio , con mayor frecuencia la mediana o, a veces, la media del conjunto de datos.

$${\ displaystyle D_ {i} = | x_ {i} -m (X) |}

dónde

D _i es la desviación absoluta,

x _i es el elemento de datos

y m ( X ) es la medida elegida de la tendencia central del conjunto de datos, a veces la media ($${\ displaystyle {\ overline {x}}}), pero más a menudo la mediana .

Medidas [ editar ]

Ver también: exactitud y precisión.

Desviación media firmado [ editar ]

Artículo principal: media desviación firmada

Para un estimador imparcial , el promedio de las desviaciones firmadas en todo el conjunto de todas las observaciones del valor del parámetro de población no observada promedia cero en un número arbitrariamente grande de muestras. Sin embargo, por construcción, el promedio de las desviaciones con signo de los valores con respecto al valor medio de la muestra siempre es cero, aunque la desviación con signo promedio de otra medida de tendencia central, como la mediana de la muestra, no necesita ser cero.

Dispersion [ editar ]

Las estadísticas de la distribución de las desviaciones se utilizan como medidas de dispersión estadística .

• La desviación estándar es la medida de dispersión utilizada con frecuencia: utilizadesviaciones cuadradas y tiene propiedades deseables, pero no es robusta .
• La desviación absoluta promedio , es la suma de los valores absolutos de las desviaciones dividida por el número de observaciones.
• La desviación absoluta media es una estadística robusta que utiliza la mediana, no la media, de las desviaciones absolutas.
• La desviación absoluta máxima es una medida altamente no robusta, que utiliza la desviación absoluta máxima.

Normalización [ editar ]

Más información: Normalización (estadística).

Las desviaciones tienen unidades de la escala de medición (por ejemplo, los medidores si miden longitudes). Uno puede no dimensionalizar de dos maneras.

Una forma es dividiendo por una medida de la escala ( dispersión estadística ), con mayor frecuencia, ya sea la desviación estándar de la población, en la estandarización , o la desviación estándar de la muestra, en studentizing (por ejemplo, studentizados residual ).

En cambio, se puede escalar por ubicación, no por dispersión: la fórmula para una desviación porcentual es el valor observado menos el valor aceptado dividido por el valor aceptado multiplicado por el 100%.