La geometría sólida constructiva ( CSG ) (anteriormente llamada geometría sólida binaria computacional ) es una técnica utilizada en el modelado de sólidos . La geometría sólida constructiva permite a un modelador crear una superficie u objeto complejo utilizando operadores booleanos para combinar objetos más simples. [1]potencialmente generando objetos visualmente complejos al combinar algunos primitivos. [2]
En gráficos de computadora en 3D y CAD , CSG se usa a menudo en el modelado de procedimientos . El CSG también se puede realizar en mallas poligonales , y puede o no ser de procedimiento y / o paramétrico.
Trabajos [ editar ]
Los objetos sólidos más simples utilizados para la representación se llaman primitivos . Típicamente son objetos de forma simple: cuboides , cilindros , prismas , pirámides , esferas , conos . [1] El conjunto de primitivos permitidos está limitado por cada paquete de software. Algunos paquetes de software permiten CSG en objetos curvos, mientras que otros paquetes no lo hacen.
Se dice que un objeto se construye a partir de primitivas por medio de operaciones permitidas , que son típicamente operaciones booleanas en conjuntos : unión , intersección y diferencia , así como transformaciones geométricas de esos conjuntos. [1]
Una primitiva puede típicamente describirse mediante un procedimiento que acepta cierto número de parámetros; por ejemplo, una esfera puede ser descrita por las coordenadas de su punto central, junto con un valor de radio. Estas primitivas se pueden combinar en objetos compuestos mediante operaciones como estas:
Combinando estas operaciones elementales, es posible construir objetos con alta complejidad a partir de los simples.
Raytracing [ editar ]
La representación de geometría sólida constructiva es particularmente simple cuando se realiza un trazado de rayos . Los trazadores de rayos intersectan un rayo con las dos primitivas que están siendo operadas, aplican el operador a los intervalos de intersección a lo largo del rayo 1D y luego toman el punto más cercano a la cámara a lo largo del rayo como resultado.
Aplicaciones [ editar ]
La geometría sólida constructiva tiene varios usos prácticos. Se utiliza en los casos en que se desean objetos geométricos simples, [ cita requerida ] o donde la precisión matemática es importante. [3] Casi todos los paquetes CAD de ingeniería utilizan CSG (donde puede ser útil para representar cortes de herramientas y características donde las partes deben encajar).
El motor Quake y el motor Unreal usan este sistema, al igual que Hammer (el editor de nivel de motor de Source Source ), y Torque Game Engine / Torque Game Engine Advanced . CSG es popular porque un modelador puede usar un conjunto de objetos relativamente simples para crear una geometría muy complicada. [2] Cuando CSG es de procedimiento o paramétrico, el usuario puede revisar su compleja geometría cambiando la posición de los objetos o cambiando la operación booleana utilizada para combinar esos objetos.
Una de las ventajas de CSG es que puede asegurar fácilmente que los objetos sean "sólidos" o impermeables si todas las formas primitivas son impermeables. [4] Esto puede ser importante para algunas aplicaciones de computación de manufactura o ingeniería. En comparación, cuando se crea una geometría basada en representaciones de límites , se requieren datos topológicos adicionales, o se deben realizar verificaciones de consistencia para asegurar que la descripción de límite dada especifique un objeto sólido válido. [1]
Una propiedad conveniente de las formas CSG es que es fácil clasificar los puntos arbitrarios como dentro o fuera de la forma creada por CSG. El punto simplemente se clasifica contra todas las primitivas subyacentes y se evalúa la expresión booleana resultante. [5] Esta es una calidad deseable para algunas aplicaciones como el trazado de rayos . [5]
Conversión de mallas a CSG [ editar ]
Dado que los modelos CSG están parametrizados por construcción, a menudo son favorables a las mallashabituales cuando se trata de aplicaciones donde el objetivo es fabricar modelos personalizados. Para tales aplicaciones puede ser interesante convertir mallas ya existentes a árboles CSG. Este problema de convertir automáticamente las mallas en árboles CSG se denomina CSG inverso .
Se requiere que el árbol CSG resultante ocupe el mismo volumen en el espacio 3D que la malla de entrada y tenga un número mínimo de nodos. Se prefieren soluciones simples para asegurar que el modelo resultante sea fácil de editar. Resolver este problema es un desafío debido al gran espacio de búsqueda que se debe explorar. Combina parámetros continuos, como la dimensión y el tamaño de las formas primitivas, y parámetros discretos, como los operadores booleanos utilizados para construir el árbol CSG final.
Los métodos deductivos resuelven este problema mediante la construcción de un conjunto de medios espaciosque describen el interior de la geometría. Estos espacios intermedios se utilizan para describir primitivas que se pueden combinar para obtener el modelo final. [6]
Otro enfoque desacopla la detección de formas primitivas y el cálculo del árbol CSG que define el modelo final. Este enfoque explota la capacidad de las herramientas modernas de síntesis de programas para encontrar un árbol CSG con una complejidad mínima. [7]
También hay enfoques que utilizan algoritmos genéticos para optimizar de forma iterativa una forma inicial hacia la forma de la malla deseada. [8]
Aplicaciones notables con soporte CSG [ editar ]
Lenguajes genéricos de modelado y software [ editar ]
El trazado de rayos y transporte de partículas [ editar ]
CAD [ editar ]
- AutoCAD
- BRL-CAD
- CATIA
- FreeCAD
- NX CAD
- OpenSCAD
- Pro / Ingeniero
- Realsoft 3D
- Rinoceronte
- Autocad
- Conjunto de CAD mecánico de SolidWorks
- VectorWorks Architect
Juegos [ editar ]
- Godot [9]
- GtkRadiant
- Roblox Studio - desde 2014
- Unity (modo de edición y en tiempo real, requiere el uso de complementos comprados en Asset Store)
- Irreal
- Editor de Valve Hammer
Otros [ editar ]
- 3Delight
- Aqsis (a partir de la versión 0.6.0) [10]
- Blender (Blender es un editor de malla de superficie, pero puede hacer un CSG simple usando meta objetos y usando el modificador booleano en objetos de malla)
- Clara.io
- Geant4
- MCNP
- SketchUp
En matemática , la geometría de contacto es el estudio de una estructura geométrica en variedades lisas dada por una distribución dehiperplano en el paquete tangente que satisface una condición llamada "no integrabilidad completa". De manera equivalente, tal distribución puede darse (al menos localmente) como el núcleo de una forma única diferencial, y la condición de no integrabilidad se traduce en una condición máxima de no degeneración en la forma. Estas condiciones son opuestas a dos condiciones equivalentes para la " integrabilidad completa " de una distribución de hiperplano, es decir, que sea tangente a una foliación de codimension uno en la variedad, cuya equivalencia es el contenido delTeorema de Frobenius .
La geometría de contacto es, en muchos aspectos, una contraparte impar de la geometría simpléctica , una estructura en ciertas variedades de dimensiones parciales. Tanto el contacto como la geometría simpléctica están motivados por el formalismo matemático de la mecánica clásica , donde se puede considerar el espacio de fase de dimensión uniforme de un sistema mecánico o la hipersuperficie de energía constante, que, al ser una de dimensión, tiene una dimensión impar.
Aplicaciones [ editar ]
Al igual que la geometría simpléctica, la geometría de contacto tiene amplias aplicaciones en física , por ejemplo, óptica geométrica , mecánica clásica , termodinámica , cuantización geométrica , sistemas integrables y teoría de control . La geometría de contacto también tiene aplicaciones para la topología de baja dimensión ; por ejemplo, ha sido usado por Kronheimer y Mrowka para probar la propiedad P conjetura , por Michael Hutchings para definir un invariante de tres variedades lisas, y por Lenhard Ng para definir invariantes de nudos. También fue utilizado porYakov Eliashberg para derivar una caracterización topológica de múltiples de Stein de dimensión al menos seis.
Formularios de contacto y estructuras [ editar ]
Una estructura de contacto en una variedad dimensional impar es una familia que varía suavemente de codimensionamiento uno subespacios de cada espacio tangente de la variedad, satisfaciendo una condición de no integrabilidad. La familia se puede describir como una sección de un paquete de la siguiente manera:
Dado un colector liso M n- dimensional y un punto p ∈ M , un elemento de contacto de M con punto p de contacto es un subespacio lineal ( n - 1) dimensional del espacio tangente a M en p . [1] [2] Un elemento de contacto puede ser dado por el núcleo de una función lineal en el espacio tangente a M en p . Sin embargo, si un subespacio está dado por el núcleo de una función lineal ω, entonces también estará dado por los ceros de λω donde λ ≠ 0 es cualquier número real distinto de cero. Por lo tanto, todos los núcleos de {λω: λ ≠ 0} dan el mismo elemento de contacto. De ello se deduce que el espacio de todos los elementos de contacto de M puede identificarse con un cociente del haz cotangente T * M (con la sección cero).eliminado), [1] a saber:
Una estructura de contacto en una variedad dimensional impar M , de dimensión 2 k + 1 , es una distribuciónuniforme de los elementos de contacto, indicada con ξ, que es genérica en cada punto. [1] [2] La condición de genérico es que ξ no es integrable .
Supongamos que tenemos una distribución uniforme de los elementos de contacto, ξ, dada localmente por un diferencial de 1-forma α; Es decir, una sección lisa del haz cotangente. La condición de no integrabilidad se puede dar explícitamente como: [1]
Tenga en cuenta que si ξ viene dado por el diferencial de 1-forma α, entonces la misma distribución está dada localmente por β = ƒ⋅α , donde ƒ es una función suave que no es cero . Si ξ es co-orientable, entonces α se define globalmente.
Propiedades [ editar ]
Del teorema de Frobenius sobre la integrabilidad se desprende que el campo de contacto ξ es completamente no intratable . Esta propiedad del campo de contacto es más o menos lo contrario de ser un campo formado por los planos tangentes a una familia de hipersuperficies que no se superponen en M . En particular, no puede encontrar una hipersuperficie en M cuyos espacios tangentes concuerden con, incluso localmente. De hecho, no existe una sub-matriz de dimensión mayor que k cuyos espacios tangentes se encuentran en.
Relación con estructuras simplécticos [ editar ]
Una consecuencia de la definición es que la restricción de la forma 2 ω = d α a un hiperplano en ξ es una forma 2 no degenerada. Esta construcción proporciona cualquier colector de contactos M con un naturales haz simpléctico de rango uno menor que la dimensión de M . Tenga en cuenta que un espacio vectorial simpléctico siempre es paridimensional, mientras que los colectores de contacto deben ser impares.
El paquete cotangente T * N de cualquier variedad n- dimensional N es en sí mismo una variedad (de dimensión 2 n ) y soporta naturalmente una estructura simpléctica exacta ω = d λ. (Esta forma de 1 λ se llama a veces la forma de Liouville ). Hay varias formas de construir una variedad de contacto asociada, una de dimensión 2 n - 1, una de dimensión 2 n + 1.
- Proyectivización
Deje que M sea el projectivization del haz cotangente de N : de este modo M es de haz de fibras sobre una Mcuya fibra en un punto x es el espacio de líneas en T * N , o, equivalentemente, el espacio de hiperplanos en T N. El 1-forma λ no desciende a una verdadera 1-forma de M . Sin embargo, es homogénea de grado 1, y por lo que define una 1-forma con valores en la línea de haz de O (1), que es el doble del haz fibrewise línea tautológica de M . El núcleo de esta forma 1 define una distribución de contactos.
- Superficies energéticas
Supongamos que H es una función suave en T * N , que E es un valor regular para H , de modo que el nivel establecidoes un submanchold suave de codimension 1. Un campo vectorial Y se llama un campo vectorial de Euler (o Liouville) si es transversal a L y simlépticamente conforme, lo que significa que la derivada de Lie de d λ con respecto a Y es un múltiplo de d λ en un barrio de l .
Entonces la restricción de a L es una forma de contacto en L .
Esta construcción se origina en la mecánica hamiltoniana , donde H es un hamiltoniano de un sistema mecánico con el espacio de configuración N y el espacio de fase T * N , y E es el valor de la energía.
- La unidad del paquete cotangente.
Elija una métrica riemanniana en la variedad N y deje que H sea la energía cinética asociada. Luego, el conjunto de niveles H = 1/2 es el paquete cotangente unitario de N , un colector liso de dimensión 2 n -1 que cubre Nsobre las fibras, que son esferas. Entonces, la forma de Liouville restringida a la unidad cotangente es una estructura de contacto. Esto corresponde a un caso especial de la segunda construcción, donde el flujo del campo vectorial de Euler Y corresponde a la escala lineal de los momentos de p, dejando las q fijas. El campo vectorial R , definido por las igualdades.
- λ ( R ) = 1 y d λ ( R , A ) = 0 para todos los campos vectoriales A ,
se llama campo vectorial Reeb y genera el flujo geodésico de la métrica de Riemann. Más precisamente, utilizando la métrica de Riemann, se puede identificar cada punto del haz cotangente de N con un punto del haz tangente de N , y luego el valor de R en ese punto del paquete cotangente (unidad) es la correspondiente (unidad ) vector paralelo a N .
- Primer paquete de jet
Por otra parte, uno puede construir un contacto colector M de dimensión 2 n + 1, considerando la primera haz de chorro de los función real en N . Este paquete es isomorfo a T * N × R utilizando la derivada exterior de una función. Con coordenadas ( x , t ), M tiene una estructura de contacto.
-
- α = dt + λ.
Por el contrario, dado cualquier colector de contacto M , el producto M x R tiene una estructura natural de colector simpléctico. Si α es un formulario de contacto en M , entonces
- ω = d ( e t α)
es una forma simpléctica en M × R , donde t denota la variable en la dirección R. Este nuevo colector se llama el symplectization (a veces symplectification en la literatura) del contacto colector M .
Ejemplos [ editar ]
Como ejemplo principal, considere R 3 , dotado de coordenadas ( x , y , z ) y la forma dz - y dx . El plano de contacto ξ en un punto ( x , y , z ) está atravesado por los vectores X 1 = ∂ y y X 2 = ∂ x + y ∂ z .
Al reemplazar las variables individuales x e y con las multivariables x 1 , ..., x n , y 1 , ..., y n , se puede generalizar este ejemplo a cualquier R 2 n +1 . Según un teorema de Darboux , cada estructura de contacto en una variedad se parece localmente a esta estructura de contacto en particular en el espacio vectorial -dimensional (2 n + 1).
Subvariedades Legendrian y nudos [ editar ]
Los subespacios más interesantes de un colector de contacto son sus submanifold de Legendrian. La no integrabilidad del campo de hiperplano de contacto en una variedad (2 n + 1) -dimensional significa que no hay submanifold de 2 n- dimensiones como su paquete tangente, incluso localmente. Sin embargo, en general es posible encontrar submanifolds n-dimensionales (incrustados o inmersos) cuyos espacios tangentes se encuentran dentro del campo de contacto. Las submanifold legendarias son análogas a las submanifolds lagrangianas de variedades simplécticas. Existe una relación precisa: el levantamiento de una sub-colección de Legendrian en una simectización de una variedad de contacto es una sub-colección de Lagrangian. El ejemplo más simple de submanifolds de Legendrian son los nudos de Legendrian.Dentro de un contacto de tres colectores. Los nudos legendarios no equivalentes pueden ser equivalentes a nudos lisos; es decir, hay nudos que son suavemente isotópicos donde la isotopía no puede ser elegida para ser un camino de nudos legendarios.
Los sub-colectores legendarios son objetos muy rígidos; por lo general, hay infinitas clases de incrustaciones de isotopía de Legendrian que son todas perfectamente isotópicas. La teoría del campo simpléctico proporciona invariantes de submanifold de Legendrian llamada homología de contacto relativa que a veces puede distinguir distintas submanifolds de Legendrian que son topológicamente idénticas (es decir, suavemente isotópicas).
Reeb vector de campo [ editar ]
Si α es una forma de contacto para una estructura de contacto dada, el campo R del vector Reeb se puede definir como el elemento único del kernel (unidimensional) de dα, de modo que α ( R ) = 1. Si un colector de contacto surge como un hipersuperficie de energía constante dentro de una variedad simpléctica, entonces el campo vectorial Reeb es la restricción a la sub-variedad del campo vectorial hamiltoniano asociado a la función de energía. (La restricción produce un campo vectorial en la hipersuperficie de contacto porque el campo vectorial hamiltoniano conserva los niveles de energía).
La dinámica del campo Reeb se puede utilizar para estudiar la estructura de la variedad de contacto o incluso la variedad subyacente utilizando técnicas de homología de Floer , como la teoría del campo simpléctico y, en tres dimensiones, la homología de contacto integrada.. Diferentes formas de contacto cuyos núcleos dan la misma estructura de contacto producirán diferentes campos vectoriales Reeb, cuyas dinámicas son en general muy diferentes. Los diversos sabores de la homología de contacto dependen a priori de la elección de una forma de contacto y construyen estructuras algebraicas en las trayectorias cerradas de sus campos vectoriales Reeb; sin embargo, estas estructuras algebraicas resultan ser independientes de la forma de contacto, es decir, son invariantes de la estructura de contacto subyacente, de modo que al final, la forma de contacto puede verse como una opción auxiliar. En el caso de la homología de contacto incrustada, se obtiene una invariante de los tres colectores subyacentes, es decir, la homología de contacto incrustada es independiente de la estructura de contacto; esto permite obtener resultados que se mantienen para cualquier campo vectorial Reeb en la variedad.
Algunas observaciones históricas [ editar ]
Las raíces de la geometría de contacto aparecen en el trabajo de Christiaan Huygens , Isaac Barrow e Isaac Newton . La teoría de las transformaciones de contacto (es decir, las transformaciones que preservan una estructura de contacto) fue desarrollada por Sophus Lie , con el doble objetivo de estudiar ecuaciones diferenciales (por ejemplo, la transformación de Legendre o la transformación canónica ) y describir el "elemento de cambio de espacio", conocido desde la dualidad proyectiva. .
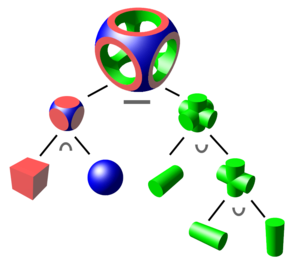













No hay comentarios:
Publicar un comentario