domingo, 8 de marzo de 2015

GEOMETRÍA - FRACTALES

Fractalismo es un movimiento artístico surgido en la última década del siglo XX, con antecedentes desde 1985,1 derivado del concepto matemático “fractal”. Katherine Hyles considera la teoría de la geometría fractal de Mendelbrot como una nueva estética. Mientras que Eva Neuer lo propone como el reconocimiento de que todo el mundo -pasado presente y futuro-; está contenido en uno mismo y que, a la vez, cada uno forma parte del todo. Lo anterior implica que al cambiar uno mismo, se cambia el mundo.- ..................................................:http://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=de91060e3caf0635eccbc10917f09614b49f15fe&writer=rdf2latex&return_to=Fractalismo








 función de Cantor, llamada así en honor de Georg Cantor, es un ejemplo de función matemática que es continua pero no absolutamente continua. También se la conoce como la escalera del Diablo.
La función de Cantor guarda una estrecha relación con el conjunto de Cantor.- ...............................:http://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=914f9db697bd24da12639561a515b49f8472ed4b&writer=rdf2latex&return_to=Funci%C3%B3n+de+Cantor

La escalera de Cantor
Sea C \subseteq [0,1] el conjunto de Cantor. La escalera de Cantor es una función f \colon [0,1] \to {\mathbb R}que tiene las siguientes propiedades:
  1. f es continua,
  2. f es no decreciente,
  3. f es constante sobre cada intervalo de [0,1] \backslash C,
  4. f ( C ) = [0,1].
cantor
Una forma de construir la escalera de Cantor es considerando una sucesión de funciones (f_n) definidas en el intervalo [0,1] mediante la relación de recurrencia f_0(x)=x,
\displaystyle{ f_{n+1}(x) = \left \{ \begin{array}{rl} f_n(3x)/2, & \text{si } 0 \leq x \leq 1/3, \\ 1/2, & \text{si } 1/3 \leq x \leq 2/3,\\ (1+ f_n(3x-2))/2, & \text{si } 2/3 \leq x \leq 1. \end{array} \right . }
Cantor_function_sequence
Se puede comprobar que la sucesión (f_n) converge uniformemente hacia una función 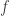f con las propiedades deseadas.
2º. Existencia de conjuntos no medibles
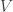Se define una relación de equivalencia en {\mathbb R} mediante x \sim y si x-y\in {\mathbb Q}. A continuación se elige un representante de cada clase de equivalencia en el intervalo [0,1]. El conjunto Vque resulta de esta elección es un conjunto no medible que se llama conjunto de Vitali. Este post contiene una discusión acerca del conjunto de Vitali. Es fácil comprobar que si E \subseteq V es medible entonces m(E)=0.
Se puede suponer sin pérdida de generalidad que A \subseteq [0,1). En efecto, como m^\ast(A)>0,existe algún n \in {\mathbb N} tal que m^\ast(A \cap [n,n+1))>0. Consideremos el conjunto B=-n+ (A \cap [n,n+1)). Tenemos B \subseteq [0,1), y como la medida exterior es invariante por traslaciones, tenemos m^\ast(B) >0. Si E \subseteq B no es medible entonces el trasladado n+E \subseteq A tampoco es medible. Sea ahora (r_n) una numeración de {\mathbb Q} \cap [0,1]. Sea V_n= r_n + V y sea E_n= V_n \cap A. Afirmamos que E_n no es medible para algún n \in {\mathbb N}. En efecto, en caso contrario, como E_n es medible, -r_n + E_n es medible, y como -r_n +E_n \subseteq V,se sigue que m(E_n)=m(-r_n+E_n)=0. Ahora tenemos
\displaystyle{A = A \cap [0,1) \subseteq A \cap \left ( \bigcup_{n=1}^\infty V_n\right )= \bigcup_{n=1}^\infty A \cap V_n =\bigcup_{n=1}^\infty E_n,}
de donde se deduce que
\displaystyle{m^\ast(A) \leq m^\ast \left ( \bigcup_{n=1}^\infty E_n \right ) \leq \sum_{n=1}^\infty m^\ast(E_n)=0,}
y hemos llegado a una contradicción.
3º. Un conjunto medible que no es boreliano
A continuación probamos la existencia de conjuntos medibles que no son borelianos. Sea f \colon [0,1] \to [0,1] la escalera de Cantor y sea g(x)=f(x)+x.
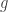Proposición. g \colon [0,1] \to [0,2] es un homeomorfismo, es decir, g es una biyección continua y su inversa es continua.
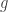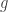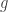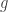Demostración. g es inyectiva porque es estrictamente creciente. g es sobreyectiva porque g(0)=0, g(1)=2. Además, g es continua por ser la suma de dos funciones continuas. Sea h = g^{-1} y probemos que h es continua. Sea G \subseteq [0,1] abierto y veamos que h^{-1}(G)=g(G)es abierto. Tenemos que [0,1] \backslash G es cerrado y acotado, y por lo tanto es compacto. Como ges continua, [0,2] \backslash g(G)= g([0,1] \backslash G) es compacto y por lo tanto es cerrado. Así llegamos a la conclusión de que h^{-1}(G)=g(G) es abierto.
Proposición. m(g ( C ))=1.
Demostración. Como 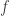f es constante sobre cada intervalo abierto (a,b) \subseteq [0,1]\backslash C,
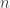resulta que m(g(a),g(b))=g(b)-g(a)=f(b)+b-f(a)-a=b-a. Sea \{I_{n,k}\}_{k=1}^{2^{n-1}} la familia de intervalos abiertos que se suprimen en la n-ésima etapa de la construcción del conjunto de Cantor. Tenemos
\displaystyle{m([0,2] \backslash g(C))= m(g([0,1]\backslash C)) = m \left ( \bigcup_{n=1}^\infty \bigcup_{k=1}^{2^{n-1}} g(I_{n,k}) \right )}
\displaystyle{=\sum_{n=1}^\infty \sum_{k=1}^{2^{n-1}} m(g(I_{n,k})= \sum_{n=1}^\infty \sum_{k=1}^{2^{n-1}} m(I_{n,k}=m([0,1] \backslash C)=1,}
de donde se deduce que m(g ( C ))=1.
Teorema. Existe un conjunto medible A \subseteq [0,1] que no es boreliano.
Demostración. Como m(g ( C ))>0, existe un conjunto no medible E \subseteq g ( C ). Sea ahora A = g^{-1}(E). Como A \subseteq C y como m( C )=0, se sigue de la completitud de la medida de Lebesgue que A es medible. Afirmamos que A no es boreliano, porque en caso contrario, como h=g^{-1} es continua, h es medible, luego E=h^{-1}(A) es medible, y hemos llegado a una contradicción.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)