Física - mecánica de fluidos

Mecánica de fluidos

El Número de Biot (Bi) es un número adimensional utilizado en cálculos de transmisión de calor. Su nombre hace honor al físico francésJean Baptiste Biot (1774-1862) y relaciona la transferencia de calor por conducción dentro de un cuerpo y la transferencia de calor porconvección en la superficie de dicho cuerpo.

Señalar que el número de Biot tiene numerosas aplicaciones, entre ellas su uso en cálculos de transferencia de calor en disipadores por aletas.

El número de Biot se define como:

En donde:

• h es el coeficiente de transferencia de calor en la superficie en W/m²K. También llamado coeficiente de película.
• L es una longitud característica en m, definida generalmente como el volumen del cuerpo dividido por su superficie externa total.
• k es la conductividad térmica del material del cuerpo W/mK.

El significado físico del número de Biot puede entenderse imaginando el flujo de calor desde una esfera caliente sumergida al fluido que la rodea. El flujo de calor experimenta dos resistencias: la primera por conducción dentro del metal y la segunda por convección desde la esfera al fluido. Se presentan dos casos límite:

• En el caso que la esfera fuera metálica y el fluido fuera agua, la resistencia por convección excederá a la de conducción y por tanto el número de Biot será inferior a uno.
• En el caso que la esfera fuera de un material aislante al calor, por ejemplo espuma de poliuretano, y el fluido fuera igualmente agua, la resistencia por conducción excederá a la de convección y el número de Biot será superior a la unidad.
• Si el número de Biot es inferior a:
  • 0.1 para placas planas
  • 0.05 para cilindros
  • 0.03 para esferas
  Implica que la conducción de calor dentro del cuerpo es mucho más rápida que la convección en la superficie de éste. Esto indica la aplicabilidad del Método del Gradiente Nulo para la resolución de problemas de calor en el transitorio.
  
  El número de Biot también aparece en las definiciones del método de las diferencias finitas usado en los problemas de calor estacionarios multidimensionales.

Una versión análoga del número de Biot, llamada habitualmente número de Biot de transferencia de materia Bi_m, se utiliza también en procesos de difusión másica.

En donde:

• h_m = es el coeficiente de transferencia de materia m/s.
• L = es una longitud característica en m.
• D_AB = es el coeficiente de difusión en m²/s.

El número de Biot, representado por Bi, es también considerado como un número adimensional, este número es usado para realizar cálculos de transmisión de calor.

Este número debe su nombre al físico francés Jean Baptiste Biot, quién nació en 1774 y falleció en 1862, este físico encontró la relación de transferencia de calor por conducción en un cuerpo, así como también la transferencia de calor por convección en la superficie de este mencionado cuerpo.

Se considera que el número de Biot posee muchas aplicaciones, una de ellas es el uso en cálculos de transferencia de calor en disipadores por aletas.

La definición del número de Biot se entiende mediante la siguiente fórmula:

Bi = hL / k

Donde:
- h es el coeficiente de transferencia de calor en la superficie en W/m2K, conocido como coeficiente de película.
- L es una longitud característica en m, definida generalmente como el volumen del cuerpo dividido por su superficie externa total.
- k es la conductividad térmica del material del cuerpo W/mK.

El número de Biot en lo que es física se entiende como el flujo de calor desde una esfera caliente que se encuentra sumergida al fluido que la rodea. Este flujo de calor experimenta dos resistencias: la primera por conducción dentro del metal y la segunda por convección desde la esfera al fluido.

Si el número de Biot es inferior a 0.1 para placas planas, a 0.05 para cilindros o a 0.03 en las esferas, implica que la conducción de calor dentro del cuerpo es mucho más rápida que la convección en la superficie de éste. lo que indica la aplicabilidad del Método del Gradiente Nulo para la resolución de problemas de calor en el transitorio.

También se puede encontrar el número de Biot en las definiciones del método de las diferencias finitas usado en los problemas de calor estacionarios multidimensionales.

Número de Eötvös (Eo)¹ es un número adimensional llamado así en honor del físico húngaro Loránd Eötvös(1848-1919). Es también conocido como Número de Bond (Bo), llamado así por el ingeniero y físico inglés Wilfrid Noel Bond (1897-1937).

Conjuntamente con el número de Morton puede ser usado para caracterizar la forma de una esfera de fluido (burbuja de aire, gota de agua, etc). El número de Eötvös es proporcional al cociente entre las fuerzas de flotación y las fuerzas debidas a la tensión superficial.

En donde:

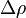•  es la diferencia de densidades entre las dos fases.
•  es la aceleración de la gravedad.
•  es una longitud característica.
•  es la tensión superficial.

Otra forma de la ecuación es:

En donde:

•  es el número de Bond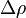
•  es la diferencia de densidades entre las dos fases.
•  es la aceleración asociada con fuerzas másicas, casi siempre gravedad.
•  es la 'longitud característica', por ejemplo, el radio de la gota de fluido o el diámetro del capilar.
•  es la tensión superficial del fluido.

El físico Loránd Eötvös cumpliría hoy 165 años.

Su trabajo se centró en gravitación y el estudio de la tensión superficial de los líquidos.

En mecánica de fluidos el número de Eötvös –Eo– es un número adimensional que junto al número de Morton –Mo– se usa para caracterizar la forma de una esfera de fluido -de una burbuja de aire, de una gota de agua, etc.-. El número de Eötvös es proporcional al cociente entre lasfuerzas de flotación y las fuerzas debidas a la tensión superficial.

Física - mecánica de fluidos

Mecánica de fluidos

número de Atwood (A) es un número adimensional utilizado en mecánica de fluidos para el estudio de las inestabilidadeshidrodinámicas en flujos de densidad estratificada. Se denomina así en honor del matemático inglés, reverendo George Atwood, creador del experimento de su nombre diseñado para verificar las leyes mecánicas del movimiento uniformemente acelerado.

Se define como la razón:

donde

 = densidad del fluido más pesado

 = densidad del fluido más ligero

De la definición se sigue que el número de Atwood toma valores entre 0 y 1: 0 cuando no hay diferencias de densidad entre los fluidos y 1 cuando el "fluido más ligero" es el vacío, típico caso de estudio en astrofísica.

El número de Atwood es un parámetro importante en el estudio de la inestabilidad de Rayleigh-Taylor y de la inestabilidad de Richtmyer-Meshkov: En la inestabilidad de Rayleigh-Taylor, la distancia de penetración de la burbujas del fluido más pesado en el interior del más ligero es una función de la escala de tiempo de aceleración, , donde  es el número de Atwood,  es la aceleración de la gravedad y  es el tiempo.

Aparatos para la enseñanza de las leyes físicas del siglo XIX

GANOT, ADOLPHE: Tratado elemental de física experimental y aplicada y de meteorología. 2º ed. París 1871.

Laboratorio de física del I.E.S. Ibáñez Martín de Lorca

MÁQUINA DE ATWOOD
COLECCIÓN	Mecánica y gravedad
FUNCIONAMIENTO	Se trata de un aparato ideado por el físico Atwood (catedrático de química en Cambridge a fines s. XVIII) y cuya finalidad es poner de manifiesto las leyes de la gravedad mediante la reproducción de la caída de los cuerpos al "ralentí" permitiendo la demostración de las leyes del movimiento uniformemente acelerado en estos movimientos, a saber: Los espacios recorridos son proporcionales a los cuadrados de los tiempos y las velocidades son proporcionales a los tiempos. Esta máquina se compone de una columna de madera (fig. 34), de unos 2m,30, de altura. En su parte superior, debajo de un fanal de vidrio, existe una polea de latón, en la cual se enrolla un hilo de seda suficientemente fino, a fin de que pueda despreciarse su peso, el cual sostiene en sus extremos dos pesos iguales M y M´. El eje de la polea, en vez de descansar sobre dos cojinetes o almohadillas fijas, se apoya sobre las convexidades cruzadas de cuatro ruedas móviles. En virtud de esta disposición, el rozamiento del eje de la polea, que trasmite su movimiento a las cuatro ruedas, es de rotación, que es mucho más suave que el que resulta cuando un cuerpo resbala sobre otro.      En la columna se halla fijo un movimiento de relojería H, regularizado por un péndulo de segundos P, merced a un escape de áncora. Este último, se halla representado en el cuadrante encima de la rueda de encuentro que ocupa el centro. Dicho escape oscila con el péndulo y al inclinarse, unas veces a la derecha, otras a la izquierda, da paso a cada oscilación, a un diente de la rueda de encuentro. El eje de ésta, lleva en su extremidad anterior, una aguja que marca los segundos, y en la posterior, detrás del cuadrante, un excéntrico figurado en E a la izquierda de la columna. Este excéntrico, que gira al mismo tiempo que la aguja, se apoya sobre una palanca D, que al moverla hace vascular, un platillo i, sostenido por dicha palanca y destinado a su vez, a sostener la masa M.     En fin, paralelamente a la columna existe una escala de madera, Q, dividida en centímetros, con objeto de medir los espacios que recorren los cuerpos al caer. En dicha escala se encuentran dos topes, o sean dos piezas móviles que, por medio de un tornillo, se pueden fijar a la altura que se quiera. Representamos estos topes en diferentes posiciones, a la derecha de la máquina, en A, A´, B, C, B´, y C´. Uno de ellos tiene la forma de un platillo, y sirve para detener la masa M; el otro, que es anular, permite que le atraviese esta masa, pero no un pequeño peso adicional que sobre ella se coloca, y que consiste en una lámina de latón más larga que el diámetro del anillo.     Sirve para disminuir la velocidad del descenso de los cuerpos, y para sustituir un movimiento uniforme a otro acelerado.   La disminución de la velocidad que esta máquina aporta a la caída de los cuerpos está basada en el principio de conservación de la cantidad de movimiento ("cuando un cuerpo en movimiento encuentra a otro en reposo, este le cede parte de su velocidad, tanto mas cuanto mayor sea la masa del segundo respecto del primero").
TEORÍA DEL EXPERIMENTO	A fin de que pueda preciarse cómo retarda el movimiento esta máquina, supongamos que la plaquita de latón m, que en nuestro dibujo está figurada en m, en m´, y en m´´, cae sola, y representemos por g su velocidad al cabo de un segundo; su cantidad de movimiento será mg. Si colocamos esta placam sobre la masa M, no podrá ya caer sino comunicando parte de su velocidad a las dos masas M y M´. Efectivamente, haciéndose equilibrio estas dos masas, queda en ellas sin efecto la gravedad; por lo tanto, la misma fuerza que hacía caer al peso m, cuando estaba solo será la que mueva ahora a este peso y a las dos masas M y M´. La cantidad de movimiento será, pues, la misma. Ahora bien, si se representa por x la velocidad al cabo de un 1 s., la cantidad de movimiento será (m+2M) x, igualándola con la que adquiere el peso m cuando cae solo, se tiene (m+2M) x=gm, de donde x=gm/m+2M. Si se supone, por ejemplo, que las masas M y M´ valgan cada una 16, siendo 1 la masa m, se encuentra x=g/33; es decir, que la velocidad será 33 veces menor que si cayese el cuerpo libremente en la atmósfera, lo cual es suficiente para que se pueda observar al cuerpo en su caída, y para que sea apenas sensible la resistencia el aire.
EXPERIENCIA	Los espacios recorridos crecen con los cuadrados de los tiempos. Para esto, parado el péndulo P, y sin que marque cero la aguja del cuadrante, se coloca el peso adicional m sobre la masa M, y así cargada ésta, se la coloca sobre el platillo i, mantenido horizontalmente por la extremidad de la palanca D, que corresponde al cero de la escala. No sirviéndonos por de pronto más que del tope lleno, se le fija por tanteo a una distancia tal del 0 de la escala, que las dos masas m y M tarden  1 s. en caer de O a A, descenso que empieza en el momento en que, entrando en oscilación el péndulo, llega la aguja al 0 del cuadrante, porque en este punto es expulsada la palanca D por el excéntrico y se inclina el platillo i.      Admitamos que se haya encontrado de esta suerte que la altura de descenso en 1 s. es 7. Se empieza entonces de nuevo el experimento del mismo modo, pero bajando el tope a una distancia O´A´ 4 veces mayor que OA, es decir, a la 28ª división de la escala, y se observa que este espacio es recorrido exactamente en 2 s. por las masas m y M. De igual manera se encuentra que una altura 9 veces mayor, o de 63 divisiones, es recorrida en 3 s., y así sucesivamente. Queda comprobada la 2ª  ley.     Para cerciorarse de la 3ª, recuérdese que en el movimiento acelerado se entiende por velocidad, en un momento dado, la del movimiento uniforme que sucede al acelerado. De consiguiente, para comprobar la ley que sigue en su variación la velocidad de un cuerpo al caer, basta medir la velocidad del movimiento uniforme que reemplaza sucesivamente al acelerado, después de 1, 2, 3 ..., segundos de descenso.      La sustitución del movimiento uniforme al acelerado, se obtiene por medio del tope anular B.  Para esto se empieza colocando el último a una distancia tal, que las dos masas m y M reunidas empleen en llegar a B  1 s., como en el primer experimento. Detenida entonces la masa adicional m por el anillo B, y continuando sola su descenso la masa M, se coloca el platillo en C, debajo de B, mediando un intervalo conveniente para que la masa M tarde un segundo en pasar de uno a otro tope. De O´´ a B el movimiento es uniformemente acelerado, y de B a C es uniforme; porque, detenido el peso m por el anillo B, ya no obra la gravedad desde B a C, y el movimiento sólo continúa en virtud de la inercia. El número de las divisiones de la escala recorridas por la masa M, de uno a otro tope, representa, pues, la velocidad adquirida por las dos masas m y M al cabo de 1 s.      Empezando entonces de nuevo el experimento, se baja el anillo B a B´, o sea a una distancia tal, que las dos masas M y m tarden 2 s. en caer de O´´ a B´, y luego se fija el segundo tope C´ a una distancia del primero doble de la que los separaba en un principio, es decir, doble de BC. Al caer las dos masas durante 2 s., con movimiento uniformemente acelerado, del punto O´´´ al B´, se encuentra que la masa M recorre sola en 1 s. el intervalo B´C´ que separa los dos topes. La velocidad adquirida al cabo de 2 s. es, por consiguiente, doble de la que se adquiere después de uno. De igual manera se comprueba que después de tres, cuatro segundos, la velocidad es tres, cuatro veces mayor.
RETARDO DE LA MÁQUINA	Si la masa adicional m cayese libremente, adquiriría al cabo del primer segundo una velocidad g. Unidas la m y la M, la velocidad común será menor. Si llamamos g', se verificará g/g'=(m+2M)/m [ec. 1]. Es fórmula nos dice que podemos hacer la velocidad g' tan pequeña como queramos, aumentando Mcon respecto a m. Pero de la misma ec 1 se deduce que: g=((m+2M)/m)g' en la que vemos que para pasar de la velocidad g, (masa m sola) a la velocidad g' (m+M) basta multiplicar g' por la cantidad constante (m+2M)/m.

autocorrelación es una herramienta matemática utilizada frecuentemente en el procesado de señales.

La función de autocorrelación se define como la correlación cruzada de la señal consigo misma. La función de autocorrelación resulta de gran utilidad para encontrar patrones repetitivos dentro de una señal, como por ejemplo, la periodicidad de una señal enmascarada bajo el ruido o para identificar la frecuencia fundamental de una señal que no contiene dicha componente, pero aparecen numerosas frecuencias armónicas de esta.- ..................................................:https://es.wikipedia.org/w/index.php?title=Autocorrelaci%C3%B3n&printable=yes

La autocorrelación se puede definir como la correlación entre miembros de series de observaciones ordenadas en el tiempo (información de series de tiempo) o en el espacio (información de corte de transversal). El modelo de regresión lineal supone que no debe existir autocorrelación en los errores , es decir, el término de perturbación relacionado con una observación cualquiera no debería estar influenciado por el término de perturbación relacionado con cualquier otra observación.

para todo

Causas de la Autocorrelación

Algunas de las causas son las siguientes :

Trabajo con datos de serie temporal: cuando se trabaja con datos de corte longitudinal (p.e.: una variable explicativa cuyas observaciones correspondan a valores obtenidos en instantes temporales sucesivos), resulta bastante frecuente que el término de perturbación en un instante dado siga una tendencia marcada por los términos de perturbación asociados a instantes anteriores. Este hecho da lugar a la aparición de autocorrelación en el modelo.

Especificación errónea en la parte determinista del modelo (autocorrelación espuria):

1. Omisión de variables relevantes: en tal caso, las variables omitidas pasan a formar parte del término de error y, por tanto, si hay correlación entre distintas observaciones de las variables omitidas, también la habrá entre distintos valores de los términos de perturbación.

2. Especificación incorrecta de la forma funcional del modelo: si usamos un modelo inadecuado para describir las observaciones (p.e.: un modelo lineal cuando en realidad se debería usar un modelo cuadrático), notaremos que los residuos muestran comportamientos no aleatorios (i.e.: están correlacionados).

Transformaciones de los datos: determinadas transformaciones del modelo original podrían causar la aparición de autocorrelación en el término de perturbación del modelo transformado (incluso cuando el modelo original no presentase problemas de autocorrelación).

Trabajo con modelos dinámicos: cuando se trabaja con series temporales suele ser habitual considerar modelos de regresión que incluyan no sólo los valores actuales sino también los valores retardados (pasados) de las variables explicativas. Es el caso de un modelo de retardos distribuidos de orden s o RD(s):

Otro tipo de modelo dinámico que presentaría problemas de autocorrelación sería aquel que incluyese entre sus variables explicativas uno o más valores retardados de la variable dependiente. Este otro tipo de modelo dinámico se conoce como modelo autorregresivo de orden s o AR(s):

Otra causa común de la autocorrelación es la existencia de tendencias y ciclos en los datos. Es decir, la mayoría de las variables económicas no son estacionarias en media. Esto significa que si la variable endógena del modelo tiene una tendencia creciente o presenta un comportamiento cíclico que no es explicado por las exógenas, el término de error recogerá ese ciclo o tendencia.

Consecuencias de la Autocorrelación:

La consecuencia más grave de la autocorrelación de las perturbaciones es que la estimación MCO deja de ser eficiente y la inferencia estadística también se verá afectada. Las consecuencias dependen del tipo de autocorrelación (positiva o negativa):

1. Cuando se tiene autocorrelación positiva, la matriz de varianza y covarianza de los residuos esta subestimada, si el tipo de autocorrelación es negativa, se tiene una sobrestimación de la misma.

2. Cuando se tiene autocorrelación positiva, la matriz de varianza y covarianza de los coeficientes (betas) esta subestimada, si el tipo de autocorrelación es negativa, se tiene una sobrestimación de la misma.

3. Cuando se tiene autocorrelación positiva, los intervalos de confianza son angostos, si el tipo de autocorrelación es negativa, se tienen intervalos de confianza más amplios.

4. Cuando se tiene autocorrelación positiva, se tiende a cometer error tipo I (rechazar la hipótesis nula cuando es verdadera), si el tipo de autocorrelación es negativa, se tiende a cometer error tipo II (no rechazar la hipótesis nula cuando es falsa).

5. Los son lineales, insesgados, pero ineficientes (no tienen varianza mínima).

6. Las pruebas y pierden validez.

Detección de la Autocorrelación:

Para analizar la posible presencia de autocorrelación en el modelo se suele recurrir a dos técnicas complementarias: (1) el análisis gráfico de los residuos (obtenidos al realizar la regresión por MCO), y (2) los contrastes de hipótesis específicos (test de Durbin-Watson, test h de Durbin, test de Breusch-Godfrey, test Q de Box-Pierce, etc.).

Análisis Gráfico:

Al realizar la regresión por MCO, se pueden graficar los residuos (o, alternativamente, los residuos estandarizados, es simplemente dividir por el error estandar de la estimación ) frente al tiempo. Dado que los residuos MCO son estimadores consistentes de los términos de perturbación, si se aprecian en el gráfico anterior patrones de comportamiento sistemático (no aleatorio) podremos afirmar que los términos de perturbación presentan algún tipo de autocorrelación.

Contrastes:

Test de Durbin-Watson

Es la prueba mas conocida para detectar correlación serial; permite contrastar si el término de perturbación está autocorrelacionado. Dicha prueba presenta algunos supuestos:

Es válido para autocorrelación serial de 1° orden en los residuos, no aplica para modelos con variable dependiente rezagada como variable explicativa, las variables explicativas son no estocásticas (son fijas en muestreo repetido), el modelo de regresión lineal debe incluir el intercepto, y no hay observaciones faltantes en los datos.

Una vez hallado DW, es posible usar su valor para estimar el coeficiente de autocorrelación simple mediante la expresión:

El estadístico DW es un valor comprendido entre 0 y 4. Como se observa en el siguiente gráfico, para valores de DW cercanos a 2 no rechazaremos la hipótesis nula, por el contrario, para valores de DW alejados de 2, sí rechazaremos la hipótesis nula

Tabla de decisión:

, se rechaza , existe autocorrelación positiva.

, se rechaza , existe autocorrelación negativa.

, no se rechaza , no existe autocorrelación.

o , el contraste no es concluyente.

Los pasos a seguir de este contraste son:

1. Estimación por mínimos cuadrados ordinarios (MCO) del modelo de regresión.

2. Cálculo de los residuos MCO.

3. Obtención del estadístico d (experimental) de Durbin-Watson.

4. Búsqueda de los niveles críticos del contraste.

5. Aplicación de la regla de decisión.

Un inconveniente que presenta este contraste es que a veces puede no ser concluyente, por lo que hay que considerar, utilizando otros criterios, si existe o no autocorrelación.

Ejemplo en Stata:

Se trabajara con la base de datos PHILLIPS.DTA, la cual contiene las siguientes variables:

, indica el año.

, es la tasa de inflación.

, es la tasa de desempleo.

Con el fin de realizar estimaciones de series de tiempo en Stata, es importante escribir el siguiente comando:

tsset year

Donde es la variable que contiene los años.

Automáticamente el sistema reconoce la serie de tiempo, y muestra:

time variable: year, 1948 to 1996

Salida en Stata: reg inf unem

Source | SS df MS Number of obs = 49

-------------+------------------------------ F( 1, 47) = 2.62

Model | 25.6369575 1 25.6369575 Prob > F = 0.1125

Residual | 460.61979 47 9.80042107 R-squared = 0.0527

-------------+------------------------------ Adj R-squared = 0.0326

Total | 486.256748 48 10.1303489 Root MSE = 3.1306

------------------------------------------------------------------------------

inf | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

unem | .4676257 .2891262 1.62 0.112 -.1140213 1.049273

_cons | 1.42361 1.719015 0.83 0.412 -2.034602 4.881822

------------------------------------------------------------------------------

Una vez estimada la regresión, se procede a ejecutar el siguiente comando con el cual se obtiene el estadístico Durbin-Watson:

estat dwatson o dwstat

Durbin-Watson d-statistic( 2, 49) = .8027005

Si se quiere estimar el Durbin-Watson por las ventanas en Stata 9, la ruta a seguir es:

Statistics/time-series/tests/time series epecification tests after regress

Automáticamente se despliega el siguiente recuadro, en donde se muestra la opción a seleccionar, y le damos OK.

La ruta a seguir en Stata 8.2 es:

Statistics/time-series/tests/Durbin-Watson d statistics after regress

Automáticamente se despliega el siguiente recuadro, en donde se muestra la opción a seleccionar, y le damos OK.

Teniendo en cuenta que DW es 0.8027, gráficamente se tiene:

Por tanto se rechaza la hipótesis nula, hay autocorrelación.

Prueba de Breusch – Godfrey (BG) sobre autocorrelación de orden superior

Este estadístico es muy sencillo de calcular y resuelve los problemas del contraste de Durbin-Watson; por ejemplo, los regresores incluidos en el modelo pueden contener valores rezagados de la variable dependiente, es decir, , etc. Pueden aparecer como variables explicativas.

Supóngase que el termino de perturbación es generado por el siguiente esquema autorregresivo de orden :

Donde es un término de perturbación puramente aleatorio con media cero y varianza constante.

Dado el modelo anterior, la hipótesis será:

No hay autocorrelación de ningún orden.

Dicha hipótesis puede ser probada de la siguiente manera:

1. Estimación por MCO del modelo de regresión y obtención de los residuos MCO

.

2. Estimación de una regresión auxiliar de los residuos sobre p retardos de los

mismos, .

3. Obtención del coeficiente de determinación ( ) de la regresión auxiliar ( ).

4. Si el tamaño de la muestra es grande, Breusch y Golfrey han demostrado que:

se distribuye con con g.l.

5. Si el valor calculado excede el valor critico de al nivel de significancia seleccionado, se puede rechazar la hipótesis nula, en cuyo caso, por lo menos un es significativamente diferente de cero (se admite que hay autocorrelación), en caso contrario no habría autocorrelación.

Ejemplo en Stata:

El comando a ejecutar es:

estat bgodfrey o bgodfrey

Breusch-Godfrey LM test for autocorrelation

---------------------------------------------------------------------------

lags(p) | chi2 df Prob > chi2

-------------+-------------------------------------------------------------

1 | 18.472 1 0.0000

---------------------------------------------------------------------------

H0: no serial correlation

De acuerdo a la salida anterior, se puede observar que el p-valor asociado al es 0.000, lo cual confirma la presencia de autocorrelación.

Si se quiere estimar la prueba Breusch – Godfrey por las ventanas en Stata 9, la ruta a seguir es:

Statistics/time-series/tests/time series epecification tests after regress

utomáticamente se despliega el siguiente recuadro, en donde se muestra la opción a seleccionar, y le damos OK.

La ruta a seguir en Stata 8.2 es:

Statistics/time-series/tests/Breusch-Godfrey LM test for autocorrelation

Automáticamente se despliega el siguiente recuadro, en donde se muestra la opción a seleccionar, y le damos OK.

Como solucionar la autocorrelación

Cuando es conocido:

1. se tiene:

(a)

(b)

2. Multiplico (b) por , y se tiene:

(c)

4. Se resta (a)-(c):

5.

(d)

Donde

6. Estimo (d) por MCO.

Cuando desconocida:

Se utiliza en algoritmo de Cochrane Orcutt: Considérese el siguiente modelo:

(e)

Y supóngase que , es generado por el esquema AR(1):

Cochrane Orcutt recomienda realizar los siguientes pasos:

1. Estimar (e) por MCO y se obtener .

2. Utilizando los residuos estimados , realizo las siguiente regresión:

(f)

3. Utilizando obtenido en la regresión anterior, efectúese la ecuación en diferencia planteada en (d) por MCO.

4. Obtengo los y los sustituyo en (a).

5. Se estima nuevamente:

; donde es la estimación de de (f).

6. Se continúan haciendo estimaciones, y se suspenden las iteraciones cuando las estimaciones consecutivas de difieren en una cantidad muy pequeña, es decir, en menos de 0.01 o 0.05.

Ejemplo en Stata:

Para ejecutar el algoritmo de Cochrane Orcutt en Stat por comando, se escribe:

prais inf unem, corc

Iteration 0: rho = 0.0000

Iteration 1: rho = 0.5727

Iteration 2: rho = 0.7160

Iteration 3: rho = 0.7611

Iteration 4: rho = 0.7715

Iteration 5: rho = 0.7735

Iteration 6: rho = 0.7740

Iteration 7: rho = 0.7740

Iteration 8: rho = 0.7740

Iteration 9: rho = 0.7741

Iteration 10: rho = 0.7741

Cochrane-Orcutt AR(1) regression -- iterated estimates

Source | SS df MS Number of obs = 48

-------------+------------------------------ F( 1, 46) = 4.33

Model | 22.4790685 1 22.4790685 Prob > F = 0.0430

Residual | 238.604008 46 5.18704365 R-squared = 0.0861

-------------+------------------------------ Adj R-squared = 0.0662

Total | 261.083076 47 5.55495907 Root MSE = 2.2775

------------------------------------------------------------------------------

inf | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

unem | -.6653356 .3196035 -2.08 0.043 -1.308664 -.0220071

_cons | 7.583458 2.38053 3.19 0.003 2.7917 12.37522

-------------+----------------------------------------------------------------

rho | .7740512

------------------------------------------------------------------------------

Durbin-Watson statistic (original) 0.802700

Durbin-Watson statistic (transformed) 1.593634

En la salida anterior, se puede observar el numero de iteraciones que realizó el algoritmo (en este caso fueron 10), la regresión transformada, y el DW del modelo original y el DW del modelo corregido. Se puede concluir, con el nuevo DW=1.59, que ya no existe autocorrelación, pues dicho valor se encuentra muy cerca de 2.

Física - mecánica de fluidos

El número de Arquímedes (Ar) (no debe confundirse con la constante de Arquímedes denominada, π) se atribuye al físico griegoArquímedes en su esfuerzo de investigar el movimiento de los fluidos en función de sus diferencias de densidad. Se trata de un número adimensional de la forma:

donde:

• g = aceleración gravitacional (),
• ρ_l = densidad del fluido []
• ρ = densidad del cuerpo []
• μ = viscosidad dinámica []
• L = longitud característica de un cuerpo []

En general se utiliza en transferencia de movimiento y en particular en flotación, fluidización y movimiento debido a diferencias de densidad. Es proporcional a:

El número de Arquímedes representado por Ar, recibe este nombre en honor al físico griego Arquímedes quién fue el que descubrió dicha forma de hallar su valor, debido a que investigó el movimiento de los fluidos en función de sus diferencias de densidad. Este número es un número adimensional, que se obtiene mediante la siguiente formula: Ar= (gL³(ρ-ρl)) / μ² donde: g = aceleración gravitacional (9,81 m/s²), ρl = densidad del fluido, kg/m³ ρ = densidad del cuerpo, kg/m³ μ = viscosidad dinámica, kg/sm L = longitud característica de un cuerpo m. Entonces el número de Arquimedes, es usado en transferencia de movimiento y en particular en flotación, fluidización y movimiento, esto se debe a las diferencias de densidad que existen, lo que crea la proporcionalidad de: (Fuerzas Gravitacionales)  (Fuerzas Viscosas) Se dice que en el siglo III a.C., el rey Hierón II ordenó que le hagan una corona de oro, hecha de un lingote de puro oro. Cuando se terminó esta corona y fue entregada al rey, este noto que la corona podía haber sido sustituido en parte por plata, es por eso que el rey Hierón llama a Arquímedes, para que resuelva esta duda. Arquímedes trató de calcular la densidad de la corona para determinar si era oro puro, luego trato de conocer el volumen, pero como el rey no quería fundir la corona, Arquímedes no pudo moldearla de forma que hiciera más fácil el cálculo del volumen. Un día, cuando Arquimedes tomaba un baño en una tina, se dió cuenta que el agua subía cuando él se sumergía, empezo a asociar conceptos: él al sumergirse estaba desplazando una cantidad de agua que equivaldría a su volumen, determinando que si sumergía la corona en agua, era posible medír la cantidad de agua desplazada y asi determinar su volumen. Llegó a la conmclusión que si la densidad era menor que la del oro, se habrían agregado materiales de otra calidad. luego tomó una pieza de plata del mismo peso que la corona, y otra de oro del mismo peso que la corona, los sumergió en una vasija de agua hasta el tope, introdujo la pieza de plata y midió la cantidad de agua derramada, hizo lo mismo con la pieza de oro. Así pudo determinar qué volumen equivalía a la plata y qué volumen equivalía el oro, llegando a determinar de forma exacta la cantidad de plata y oro que tenía la corona, y demostrando que la corona estaba adulterada. Método de Arquímedes doblando el número de lados k veces(Calculando a mano llegó hasta el caso k=4) k lados valor de  (por defecto) valor de  (por exceso) 0 6 3.0000000000000000 3.4641016151377546 1 12 3.1058285412302492 3.2153903091734725 2 24 3.1326286132812382 3.1596599420975005 3 48 3.1393502030468671 3.1460862151314350 4 96 3.1410319508905096 3.1427145996453683 5 192 3.1414524722854620 3.1418730499798238 6 384 3.1415576079118575 3.1416627470568485 7 768 3.1415838921483183 3.1416101766046894 8 1.536 3.1415904632280500 3.1415970343215261 9 3.072 3.1415921059992714 3.1415937487713519 10 6.144 3.1415925166921574 3.1415929273850969 11 12.288 3.1415926193653840 3.1415927220386137 12 24.576 3.1415926450336908 3.1415926707019980 13 49.152 3.1415926514507675 3.1415926578678444 14 98.304 3.1415926530550367 3.1415926546593059 15 196.608 3.1415926534561041 3.1415926538571713 16 393.216 3.1415926535563710 3.1415926536566377 17 786.432 3.1415926535814378 3.1415926536065044 18 1.572.864 3.1415926535877044 3.1415926535939711 19 3.145.728 3.1415926535892710 3.1415926535908377 20 6.291.456 3.1415926535896625 3.1415926535900544

arrastre o fricción de fluido es la fricción entre un objeto sólido y elfluido (un líquido o gas) por el que se mueve. Para un sólido que se mueve por un fluido o gas, el arrastre es la suma de todas las fuerzas aerodinámicas o hidrodinámicas en la dirección del flujo del fluido externo. Por tanto, actúa opuestamente al movimiento del objeto, y en un vehículo motorizado esto se resuelve con el empuje.

En la astrodinámica, dependiendo de la situación, el arrastre atmosférico se puede considerar como una ineficiencia que requiere energía adicional durante el lanzamiento del objeto al espacio o como una ventaja que simplifica el regreso desde la órbita.

Un objeto que cae a través de un gas o líquido experimenta una fuerzaen sentido opuesto a su movimiento. Se alcanza la velocidad terminalcuando la fuerza de arrastre es igual a la fuerza de la gravedad que tira de él.

aspersor de Feynman, aspersor inverso de Feynman o más correctamente el aspersor inverso es un conocido experimento mental de física para explicar el funcionamiento de la inversión de un aspersor de jardín típico. Este experimento se relaciona comúnmente con el nombre de Richard Feynman, a pesar de que no planteó el problema originalmente ni dio ninguna solución, sólo ayudó a poEl problema plantea qué sucedería si un aspersor de césped se sumergiera totalmente en agua y ésta fuera absorbida a través de él, fluyendo inversamente. Inyectando agua en los extremos del aspersor se provoca un movimiento de rotación, pero los científicos aún no se ponen de acuerdo en si girará en el mismo sentido, en sentido contrario, o no girará.

Se ha debatido mucho la solución del problema.³ Al parecer el mismo Feynman lo intentó físicamente, provocando «una pequeña explosión catastrófica».² En los últimos años, el experimento se ha realizado en numerosas ocasiones, utilizando el aire como medio en torno al aspersor, demostrando que el «aspersor inverso» gira en el mismo sentido.⁴ La Universidad de Maryland también realizó el experimento en un medio acuoso de bajo rozamiento y demostró que el aspersor de hecho gira, aunque muy lentamente, en el mismo sentido.⁵ A pesar de los numerosos experimentos que se han realizado, la comunidad científica aún debate la validez de sus resultados debido a la complejidad de las fuerzas implicadas.pularizarlo en su libro ¿Está usted de broma, Sr. Feynman? y otros de sus escritos.¹ El problema original apareció en un número de Science of Mechanics de1893, propuesto por Ernst Mach.

El problema se refiere al sentido que tomará un aspersor «inverso», es decir, sumergido en agua