Mecánica de fluidos
Esta expresión indica que la presión total ejercida sobre un fluido, depende únicamente de la profundidad, ya que la densidad  , la aceleración de gravedad y la presión atmosférica P0 son constantes, por esto se dice que la presión que se ejerce sobre un fluido, se ejerce con la misma magnitud a todas partes del fluido. Esto último es lo que se conoce como Principio de Pascal.
, la aceleración de gravedad y la presión atmosférica P0 son constantes, por esto se dice que la presión que se ejerce sobre un fluido, se ejerce con la misma magnitud a todas partes del fluido. Esto último es lo que se conoce como Principio de Pascal.
 , la aceleración de gravedad y la presión atmosférica P0 son constantes, por esto se dice que la presión que se ejerce sobre un fluido, se ejerce con la misma magnitud a todas partes del fluido. Esto último es lo que se conoce como Principio de Pascal.
, la aceleración de gravedad y la presión atmosférica P0 son constantes, por esto se dice que la presión que se ejerce sobre un fluido, se ejerce con la misma magnitud a todas partes del fluido. Esto último es lo que se conoce como Principio de Pascal.
En este caso, consideremos que el fluido se trata de un gas, y consideremos también un elemento del mismo, ubicado a una altura h, cuya base tiene un área
Ahora se integra la expresión anterior, entre P1 y P2 para la presión, y entre h1 y h2 para la altura, es decir:
En este caso la presión P2 es la presión ejercida por la atmósfera, es decir P2 = Patm, y la presión P1 es la presión ejercida sobre el elemento de fluido a la altura h, luego se tiene que:
Este resultado también se puede expresar mediante el Principio de Pascal.
Otro aspecto importante que se obtiene de la fórmula de variación de la presión con la profundidad, es la acción de la fuerza total Ft que se ejerce en esa parte del fondo del recipiente, directamente abajo del área A. Esto se obtiene de la siguiente forma:
en que F es la fuerza que se ejerce en el fondo, es decir a la profundidad total y, F0 es la fuerza ejercida por la presión atmosférica en la superficie. La cantidad Ay es el volumen del fluido en una columna cuya área transversal o en la base es A y cuya altura es y. Por lo tanto la cantidad  Ay representa la masa del fluido en esa columna. En consecuencia, la fuerza sobre cualquier área del fondo, es igual a la fuerza ejercida por la presión atmosférica sobre el área correspondiente de la superficie, más el peso del fluido contenido en la columna que descansa sobre esa área del fondo.
Ay representa la masa del fluido en esa columna. En consecuencia, la fuerza sobre cualquier área del fondo, es igual a la fuerza ejercida por la presión atmosférica sobre el área correspondiente de la superficie, más el peso del fluido contenido en la columna que descansa sobre esa área del fondo.
 Ay representa la masa del fluido en esa columna. En consecuencia, la fuerza sobre cualquier área del fondo, es igual a la fuerza ejercida por la presión atmosférica sobre el área correspondiente de la superficie, más el peso del fluido contenido en la columna que descansa sobre esa área del fondo.
Ay representa la masa del fluido en esa columna. En consecuencia, la fuerza sobre cualquier área del fondo, es igual a la fuerza ejercida por la presión atmosférica sobre el área correspondiente de la superficie, más el peso del fluido contenido en la columna que descansa sobre esa área del fondo.¿Qué es la mecánica de fluidos?
Hombre, no hace falta una larga explicación sobre esto, pero quiero detenerme en ello porque hay un par de aspectos interesantes. La mecánica de fluidos, como indica su nombre, estudia los fluidos. Sin embargo, no trata de describir todo lo relacionado con ellos: se centra en aspectos mecánicos del comportamiento de los fluidos, como su movimiento, la presión que ejercen, cómo alteran el movimiento de objetos introducidos en ellos, etc. Otras facetas del comportamiento de los fluidos, como sus cambios de temperatura y cosas así, son estudiados por la termodinámica. De hecho, si has leído aquel bloque, verás que aquí repito algunos conceptos definidos allí, aunque en un contexto diferente y haciendo énfasis en cosas distintas; disculpa la repetición, pero al ser ambos bloques introductorios, he preferido mantener ambos independientes a costa de repetir alguna cosa que otra.
La mecánica de fluidos es, por tanto, una aplicación de la mecánica, que estudia el movimiento de partículas puntuales y establece principios generales sobre su comportamiento, a un tipo especial de cuerpos: los fluidos. En cierto sentido, esto hace de esta disciplina algo derivado y no fundamental. Con esto me refiero a que sería posible describir el comportamiento de los fluidos utilizando los principios de la mecánica clásica; en otras palabras, si nos sumergimos de verdad en la mecánica de fluidos y preguntamos “¿por qué?” una y otra vez ante cada afirmación que realiza, al final llegamos a los principios básicos de la mecánica.
Sin embargo, el hecho de que la mecánica de fluidos sea teóricamente derivable a partir de la mecánica clásica no quiere decir que, en la realidad, la hayamos derivado de ella. Esta parte de la Física fue desarrollada en paralelo a la mecánica newtoniana, y contiene muchos principios físicos obtenidos de manera empírica, en varios casos siglos antes de que su explicación teórica a partir de las leyes de la dinámica fuera posible, porque esas leyes no eran aún conocidas.
Incluso ahora que nuestra mecánica está bien madura, sigue teniendo sentido utilizar una mecánica específica para los fluidos. Al fin y al cabo, estudiar el movimiento de una partícula utilizando los principios de la mecánica es bastante simple; hacerlo con dos partículas es más complicado, y hacerlo con cien algo más difícil. Pero piensa lo siguiente: un litro de agua contiene unas 3,35·1025moléculas, treinta y tres cuatrillones de moléculas en cada litro. ¿Tiene sentido determinar el movimiento de cada molécula con sus propias ecuaciones para describir el comportamiento de un litro de agua? Desde luego que no, sobre todo porque es posible hacerlo con principios que se aplican al conjunto de todas las moléculas – de ahí la existencia, incluso hoy, de la mecánica de fluidos.
En ella, en vez de tratar los fluidos como conjuntos de moléculas, se tratan como un continuo. Para comprender el concepto lo mejor, en mi opinión, es alcanzarlo llevando un proceso al límite. Imagina 1 kg de arena de playa, formada por un grano de arena de 1 kg de masa. Ahora imagina que lo partimos en dos, de modo que la arena está formada por dos granos de 0,5 kg cada uno. Si seguimos haciendo esto hasta tener granos de 1 gramo, la arena estará formada por mil granos de 1 g cada uno.
Ahora imagina que los volvemos a partir un millón de veces, y luego un millón de veces más. Tendríamos un número gigantesco de granos tan pequeños que serían invisibles, individualmente, al ojo humano. Bien, ahora imagina que repetimos el proceso hasta el infinito: la “granularidad” de la arena se haría infinitamente fina, como si triturásemos la masa con una trituradora infinitamente poderosa. El resultado es un continuo, en el que no tiene sentido hablar de las partes, sino del conjunto formado por ellas. Evidentemente la materia no es continua y los fluidos, por tanto, tampoco lo son, pero recuerda el número de moléculas de agua en un litro del líquido; la mecánica de fluidos parte de esta premisa para simplificar enormemente las cosas sin perder apenas rigor y precisión en el resultado.
¿Qué es un fluido?
Como sucede tantas otras veces, es muy fácil tener una idea intuitiva bastante razonable sobre qué es un fluido, pero dar una definición rigurosa no lo es tanto porque se trata de una “etiqueta” más o menos arbitraria que damos a ciertos medios. Dicho mal y pronto,
Un fluido es un medio capaz de fluir, es decir, de cambiar de forma y adaptarse al recipiente que lo contiene.
Esta propiedad la cumplen, en su definición ideal, los líquidos, los gases y los plasmas. Es lo que tienen en común, por mucho que se diferencien en otras cosas, y esta propiedad determina gran parte de su comportamiento en contraposición al de los sólidos. De las diferencias entre los distintos tipos de fluidos hablaremos en la próxima entrega pero, por ahora, centrémonos en lo que los une.
¡Ojo! Fluido ≠ líquido
Sí, ya sé que acabo de definir fluido, pero esta confusión está tan extendida que no puedo dejar de dedicarle su propia advertencia. Los líquidos son fluidos, pero no son los fluidos, sino simplemente un subconjunto de ellos. Tan fluidos como los líquidos son los plasmas, y tanto como ellos los gases.
Existen diferencias entre esos estados de agregación (no se comporta igual el agua que el plasma que forma el núcleo del Sol), pero todos tienen en común una propiedad fundamental, que es la que determina el hecho de que sean fluidos. De modo que un líquido siempre es un fluido, pero hay fluidos que no son líquidos. Sí, ya dejo de ser pedantón.
Así, un ladrillo es un sólido y no es capaz de fluir: tendrá siempre forma de ladrillo esté dentro de un barril, sobre tu mano o en el suelo. Sin embargo, el agua de una botella es un fluido, ya que tiene forma de botella mientras está en ella, pero si la viertes sobre tu mano se adapta a su forma; puesto que tu mano tiene huecos entre los dedos, de hecho, la gravedad terrestre hará que el fluido se escape entre ellos y caiga al suelo. Y, una vez en el suelo, se adaptará a su forma y creará un charco más o menos amplio dependiendo de la profundidad que pueda tener por la forma del terreno.
El aire dentro de un globo tiene la misma propiedad: puedes apretar la superficie del globo con un dedo creando una hendidura, y el gas del interior cambiará de forma para adaptarse a la nueva superficie del globo. Si metes el globo dentro de una caja cuadrada y lo fuerzas a tomar la forma de la caja, el aire tomará forma cuadrada como la caja, etc.
¿Y el puré de patatas?
Como he dicho muchas veces anteriormente en El Tamiz, los nombres que damos a las cosas, nuestras definiciones y nuestras ecuaciones están en nuestra cabeza y son herramientas que nos ayudan a predecir el comportamiento de las cosas, pero no forman parte de las propias cosas.
Siempre se nos enseña que hay sólidos, líquidos y gases, y que los primeros no son fluidos pero los segundos sí. Sin embargo, esos nombres idealizan comportamientos. Ningún líquido es realmente un fluido de acuerdo con la definición, y ningún sólido deja de serlo realmente. Se trata de una cuestión de grado. Por ejemplo, ¿qué es el puré de patatas? ¿Un sólido? Si así fuera daría igual la forma del recipiente en el que lo introduces, porque siempre tendría una forma propia, algo que no sucede. ¿Un fluido? No, porque sería imposible tomar puré de patatas con un tenedor, ya que fluiría entre los dientes y caería de nuevo al recipiente.
Ah, puedes pensar, depende de la consistencia del puré de patatas. Si tiene mucha leche o agua, entonces se irá aproximando a un fluido hasta que sea imposible cogerlo con un tenedor, y si tiene muy poca leche o agua, llegará un momento en el que tenga casi una forma propia, independiente del recipiente. Pero si piensas así habrás llegado, creo, a la conclusión que intento hacerte ver: es una cuestión de grado. No hay sólidos y fluidos, sino medios que se parecen más a unos o a otros. Cuando un medio se aproxima muchísimo a un comportamiento, las conclusiones teóricas derivadas de la definición serán casi idénticas a lo que sucede en la realidad y viceversa.
Esto significa, claro, que las sustancias que están “a medio camino”, como muchos plásticos, la plastilina, el puré de patatas, etc., no se definen bien mediante las definiciones de fluido o sólido. A lo largo del tiempo hemos ideado magnitudes y ecuaciones que tienen en cuenta estas desviaciones de los comportamientos ideales, como la viscosidad, y de ellas hablaremos tarde o temprano. Mi objetivo en esta ampliación es simplemente recordarte que no te dejes llevar por las etiquetas que damos a las cosas y pensar así que en la Naturaleza existe tal cosa como un “sólido”.
Hidráulica, hidrodinámica y mecánica de fluidos
La necesidad de comprender el comportamiento de los fluidos ha sido siempre imperiosa para nosotros: al fin y al cabo, nuestra vida depende de dos fluidos, el aire y el agua. Asegurar el suministro de ambos es un requisito indispensable para nuestra supervivencia, y esto significa que mucho antes de que Newton estableciera principio alguno ni supiéramos lo que es una fuerza con el menor rigor ya teníamos cierta idea sobre las características fundamentales de los fluidos y cómo manipularlos.
Esto significa que, en sus comienzos –mucho antes de recibir su nombre actual– la mecánica de fluidos era algo completamente empírico, y no tanto el campo de estudio de los científicos como de los ingenieros civiles: sin un conocimiento, aunque sea rudimentario, de la flotabilidad de los cuerpos, las variaciones de presión del agua y hasta dónde es posible elevarla y cosas parecidas, es muy difícil establecer una civilización tecnológica. Esta versión eminentemente práctica, no demasiado preocupada por principios fundamentales y sí por las aplicaciones técnicas del conocimiento, fue denominada hidráulica por su preocupación central, el agua.
Por poner un ejemplo, los romanos utilizaron sus conocimientos de hidráulica para construir canalizaciones que alimentaban de agua potable lugares alejadísimos de sus fuentes, y disponían de sistemas de tuberías y alcantarillado bastante sofisticados. Durante muchos siglos continuamos avanzando muy lentamente en nuestra comprensión del comportamiento de los fluidos de este modo empírico. El famoso principio de Arquímedes –que destriparemos a conciencia en este bloque– es un buen ejemplo de esto. Se trata de un fenómeno que puede explicarse a partir de leyes más fundamentales, pero durante siglos fue un principio natural sin necesidad de más explicación.
La ausencia de una verdadera teoría unificada sobre el comportamiento de los fluidos y, sobre todo, de las matemáticas y ecuaciones que describieran ese comportamiento, hizo que nuestro conocimiento fuera cualitativo. Por ejemplo, desde el principio fue algo evidente que la forma de la quilla de un barco influye sobre el flujo de agua sobre el casco cuando la nave se mueve por el agua, y es posible ir probando hasta obtener formas razonablemente hidrodinámicas sin utilizar ecuaciones. Por otro lado, es muy difícil alcanzar una perfección enorme en este aspecto sin un aparato teórico más avanzado, de modo que llegó un momento en el que, en casi todo lo relacionado con los fluidos, nos quedamos estancados.
Uno de los primeros en atacar el problema de una manera más científica fue Leonardo da Vinci. El divino italiano realizó multitud de experimentos bastante metódicos sobre el flujo de agua y aire alrededor de objetos, y documentó sus descubrimientos con diagramas maravillosos, como hacía casi siempre. Leonardo llegó a introducir pequeños objetos en el agua para observar su movimiento según fluía el líquido, observó los remolinos que aparecen cuando el agua fluye rápidamente sobre un cuerpo, es decir, la aparición de la turbulencia, y llegó a realizar diseños que minimizaban esa turbulencia.
Dibujo de flujo turbulento por Leonardo da Vinci.
Sin embargo, en la época de Leonardo la Física no se había casado aún con las Matemáticas –algo que empezaría a suceder con Galileo Galilei–, con lo que una auténtica teoría de fluidos no podía surgir. El propio Galileo, que yo sepa, no dedicó demasiado esfuerzo a esa tarea, pero dos de sus discípulos, Benedetto Castelli y Evangelista Torricelli, fueron de los primeros en establecer las bases de lo que se llamaría hidrodinámica, la contrapartida teórica de la hidráulica. Fíjate en que el nombre seguía estando derivado del fluido más estudiado de todos, el agua.
El problema era la complejidad del comportamiento de los fluidos: son muy difíciles de describir teóricamente, en parte por las sutiles diferencias entre fluidos y sólidos, en parte por la interacción de unas partes del fluido con otras y con las paredes que lo contienen. Por tanto, durante mucho tiempo la hidrodinámica sólo fue útil en casos muy particulares y para situaciones concretas; fuera de ellas era un desastre como predicción del comportamiento real. Una vez más, nuestras limitaciones matemáticas eran las culpables, ya que haría falta el desarrollo del cálculo infinitesimal para describir acertadamente el movimiento de los fluidos.
En el caso de fluidos en equilibrio, dado que no había movimiento del fluido, la cosa era bastante más sencilla. Su descripción, la hidrostática –un caso partícular de la hidrodinámica–, sí era posible matemáticamente con una precisión muy razonable. Torricelli estableció algunas de sus bases, pero el auténtico padre de la hidrostática y, por tanto, uno de los pioneros de la hidrodinámica, fue el francés Blaise Pascal, del que hablaremos con seguridad en este bloque.
Isaac Newton realizó algunos avances en hidrodinámica, como el estudio del flujo del agua a través de orificios y la descripción de la viscosidad, pero su principal aporte a esta ciencia fue el desarrollo del cálculo infinitesimal –probablemente de manera independiente y casi simultánea a Gottfried Leibniz–. Con esa “madurez” de las matemáticas fue posible atacar el problema de verdad, con una herramienta realmente preparada para el problema.
Otros científicos tras Newton, como Daniel Bernoulli y Jean le Rond d’Alembert, realizaron grandes avances en hidrodinámica. A estas alturas, a mediados del siglo XVIII, los científicos ya no estudiaban casos concretos del comportamiento de los fluidos, sino que trataban de establecer principios generales; por ejemplo, una de las mejores obras de d’Alembert se llama Traité des fluides. Las matemáticas nos proporcionaron, una vez más, las herramientas para dar un salto en nuestro conocimiento de los fluidos cuando el genial Leonhard Euler desarrolló las ecuaciones en derivadas parciales y las empleó para describir, por primera vez, el comportamiento general de un fluido de manera teórica.
El problema era que las ecuaciones de Euler y otras basadas en su trabajo eran desastrosas en la mayor parte de los casos, y sólo funcionaban bien de verdad en algunas situaciones. Por lo tanto, incluso en el siglo XVIII gran parte de la hidrodinámica era considerada una curiosidad teórica. Los ingenieros seguían obteniendo mejores resultados simplemente utilizando métodos puramente empíricos que recurriendo a las ecuaciones de Euler y similares.
Todo cambió en el siglo XIX. Primero, un par de físicos –un inglés, Sir George Stokes, y un francés, Claude-Louis Navier– establecieron en 1822 una ecuación que describía razonablemente bien el comportamiento de los fluidos. Posteriormente, el alemán Gustav Kirchhoff (cuyo nombre puede sonarte por la radiación de cuerpo negro). Kirchhoff refinó las ecuaciones para determinar un coeficiente relacionado con el movimiento turbulento de un fluido a través de un agujero –una de las circunstancias en las que anteriormente los resultados teóricos y los experimentales divergían enormemente–. El coeficiente no es importante ahora mismo, pero sí lo es el hecho de que Kirchhoff predijo un valor de 0,61 utilizando las ecuaciones diferenciales. El resultado experimental resultó ser 0,60. Todo cambiaría desde entonces: ya no estábamos frente a una curiosidad, sino a algo utilísimo en la práctica.
A partir de entonces se diluyó la diferencia entre hidráulica e hidrodinámica y nació una verdaderamecánica de fluidos. El nombre es, desde luego, infinitamente mejor que cualquiera de los otros dos, porque no sugiere nada acerca del agua. Hoy en día hablamos de ella cuando nos referimos al estudio de fluidos en general, pero seguimos usando los términos antiguos de hidrostática ehidrodinámica para el estudio de los líquidos –no cualquier fluido– en equilibrio o no. También utilizamos aerodinámica, por ejemplo, para referirnos al flujo de gases; como en el caso del agua, el aire forma parte del nombre por ser el gas al que más aplicamos esta teoría.
El caso es que desde la segunda mitad del XIX los ingenieros empezaron a utilizar más y más las ecuaciones diferenciales, perfeccionadas por muchos otros científicos. Ya en el siglo XX nos encontramos con un nuevo obstáculo: las matemáticas funcionaban, pero en muchos casos el comportamiento de los fluidos resultó ser caótico, es decir, endiabladamente difícil de calcular con exactitud más allá de cierto tiempo. Las matemáticas estaban preparadas, pero nuestra capacidad de cálculo no.
En este caso quien vino a nuestro rescate fue la informática. Hoy en día, para las aplicaciones prácticas que involucran conjuntos de ecuaciones no lineales son nuestros programas informáticos quienes resuelven las ecuaciones y predicen el comportamiento de los fluidos. Pero, por más complejas que se hayan hecho las matemáticas involucradas, la base teórica sigue siendo la misma: la aplicación de la mecánica newtoniana a medios continuos capaces de fluir.
Si todo esto de ecuaciones diferenciales te ha dejado un poco apabullado, no te preocupes: como Pascal, nosotros empezaremos a estudiar los fluidos en equilibrio –es decir, la estática de fluidos– para luego ir adentrándonos en asuntos más tortuosos. Lo bueno de la mecánica de fluidos es que unas bases sólidas no demasiado extensas permiten ya entender muchas cosas del mundo que nos rodea sin necesidad de meterse en camisas de once varas.




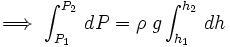




No hay comentarios:
Publicar un comentario