Mecánica de fluidos
En ingeniería y mecánica de fluidos se denomina abertura de expansión o difusor a la cámara alineada con un tubo o túnel y de diámetro mayor que el conducto que contiene un gas, para permitir una disminución de presión dentro del conducto por la dilatación del fluido.
Advección es la variación de un escalar en un punto dado por efecto de un campo vectorial. Por ejemplo: el transporte de una sustancia contaminante por la corriente de un río; en meteorología, el proceso de transporte de una propiedad atmosférica, como el calor o la humedad, por efecto del viento; en oceanografía, el transporte de ciertas propiedades, como la salinidad, por las corrientes marinas. Tales propiedades tienen una distribución espacial.
El operador advección se expresa como el producto escalar del vector velocidad por el gradiente de la propiedad:
o  son los componentes de la velocidad
son los componentes de la velocidad  según las coordenadas
según las coordenadas 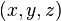 .
.
 son los componentes de la velocidad
son los componentes de la velocidad  según las coordenadas
según las coordenadas 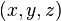 .
.
Sin embargo, en meteorología suele ser útil sustituir la coordenada vertical z por la de presión suponiendo la hipótesis hidrostática  :
:
 :
:
o
 es la velocidad vertical en coordenadas de presión;
es la velocidad vertical en coordenadas de presión; es la presión;
es la presión; es la densidad del fluido;
es la densidad del fluido; es la aceleración de la gravedad terrestre.
es la aceleración de la gravedad terrestre.
Por ejemplo, la advección de temperatura  estará expresada por:
estará expresada por:
 estará expresada por:
estará expresada por: .
.- La advección es el transporte en un fluido. El fluido se describe matemáticamente para tales procesos como un campo vector, y el material transportado como una concentración escalar de sustancia, que está presente en el fluido. Un buen ejemplo de advección es el transporte de contaminantes o sedimentos en un río: el movimiento del agua lleva estas impurezas río abajo. Otra sustancia comúnmente advectada es el calor, y aquí el fluido puede ser el agua, el aire, o cualquier otro material fluido que contenga calor. Cualquier sustancia, o propiedad conservada (como el calor) puede ser advectada, de un modo similar, en cualquier fluido.
La advección es importante para la formación de las nubes orográficas y la precipitación del agua desde las nubes, como parte del ciclo hidrológico. - En meteorología y oceanografía física, la advección a menudo se refiere al transporte de alguna propiedad de la atmósfera u océano, como calor, humedad o salinidad. La advección meteorológica u oceanográfica sigue superficies isobáricas y es, por tanto, predominantemente horizontal.
Matemáticas de la advección
La ecuación de advección es una ecuación diferencial parcial que gobierna el movimiento de un escalar conservado cuando es advectado por un campo de velocidad conocido. Se deriva usando la ley de conservación del escalar, junto con el teorema de Gauss, y tomando el límite infinitesimal.
Quizás la mejor imagen a tener en mente es el transporte de la sal vertida en un río. Si el río es al principio de agua dulce y fluye rápidamente, la forma predominante del transporte de la sal en el agua será advectiva, cuando el flujo de agua en sí mismo transportaría la sal. Si el río no estuviera fluyendo, la sal simplemente se dispersaría hacia fuera desde su fuente en una manera difusiva, lo cual no es advección.
La ecuación de advección no es simple de solucionar numéricamente: el sistema es una ecuación diferencial parcial hiperbólica, y el interés típicamente se centra en soluciones "de choque" discontinuas (que son notoriamente difíciles para manejar esquemas numéricos).
Incluso en una dimensión espacial y a velocidad constante, el sistema sigue siendo difícil de simular. 
- Aeroacústica es la rama de la acústica y mecánica de fluidos que estudia la generación de ruido debida a flujos turbulentos o fuerzas aerodinámicas interactuando con fronteras solidas. La generación de ruido también es asociada con fluctuaciones de vorticidad. Un ejemplo de este fenómeno son las resonancias eólicas producidas por el viento cuando fluye al rededor de cuerpos sumergidos en este, por ejemplo la calle de vórtices de von Kármán.- .............................: https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=41bbd2a6b962cbb6e298bdf19a70c3e7ef44ad1b&writer=rdf2latex&return_to=Aeroac%C3%BAstica
- Definición. Análisis y predicción de los niveles de ruido generados por ventiladores industriales, identificando patrones de directividad y fuentes de ruido aerodinámico. Relación entre los campos fluidodinámicos no estacionarios y la generación de ruido aerodinámico tonal. Estudio de modos de propagación y vibraciones transmitidas en forma de desequilibrios y esfuerzos mecánicos.
- Motivacióny antecedentes. La generación de ruido en ventiladores constituye un importante problema asociado al funcionamiento de unas máquinas profusamente utilizadas en diversos ámbitos de aplicación, de donde se deriva la necesidad de acometer líneas de trabajo orientadas a establecer criterios para el diseño de aparatos con menores emisiones sonoras. En los ventiladores axiales la problemática es especialmente grave porque los complejos fenómenos aerodinámicos que tienen lugar en su interior suponen una fuente de elevados niveles de ruido fácilmente propagables, máxime en aparatos no entubados (ventiladores de extracción, de chorro, de torres de refrigeración, de aire acondicionado, de aparatos electrónicos, etc.), en los que no cabe adoptar medidas correctoras mediante silenciadores. En los últimos años, parte de la investigación del Área en el ámbito de las turbomáquinas se ha encaminado hacia el estudio de las fuentes de generación de ruido en las mismas y su relación con respecto a los mecanismos no estacionarios del flujo. Trabajos pioneros en este campo trataron de identificar las fuentes de ruido a partir de las simulaciones numéricas realizadas sobre ventiladores centrífugos.
- Objetivos. Esta línea de investigación complementaria trata de identificar fuentes de ruido en turbomáquinas axiales así como estudiar su propagación hacia campo lejano. La complejidad de los modelos y la no-linealidad de la ecuación de onda han limitado hasta el momento la investigación al estudio del ruido tonal, es decir, aquél que se manifiesta a frecuencia de paso de álabe. La relación con los fenómenos de interacción descritos en capítulos anteriores ha permitido entender muchos aspectos de la generación de ruido. Utilizando analogías acústicas se han derivado mapas de ruido propagado a campo lejano y se han planteado metodologías de estudio para realizar predicciones numéricas de ruido aerodinámico. De esta línea destacan como puntos fundamentales de las investigaciones:
- Predicción numérica del ruido aerodinámico tonal
- Propagación del ruido generado aerodinámicamente a campo lejano
- Mecanismos de propagación potencial y modos fluctuantes en ventiladores axiales. Relación con los mecanismos de interacción rotor-estator.
- Ruido aerodinámico de perfiles elípticos. Modelización numérica y ensayos en túneles de viento.
- Metodología. Hasta fechas recientes, la metodología habitual de estudio acústico se ha basado en métodos empíricos, centrados en ensayos globales realizados en costosas instalaciones (bancos de ensayo, cámaras anecoicas), que aportan soluciones válidas para tipologías específicas y en limitados rangos de prestaciones, pero que no permiten obtener resultados optimizados. Adicionalmente, los conocimientos son fragmentarios, en buena parte en poder de los mejores constructores y con notables contradicciones entre autores y tendencias de diseño. Con esta línea se propone desarrollar herramientas para la cuantificación numérica y experimental de la emisión y propagación del ruido de ventiladores axiales, así como la identificación de fuentes sonoras dipolares de banda ancha, útiles respectivamente para las fases de diseño y posterior optimización de nuevos aparatos. Mediante la aplicación de modelos aerodinámicos y aeroacústicos a perfiles elípticos de ventiladores axiales, se pretende que las herramientas numéricas y experimentales sean válidas para diversas configuraciones geométricas y en amplios rangos de parámetros de funcionamiento.
Aeroacústica de ventiladores y perfiles aerodinámicos
Algunas ideas clave...
Algunos resultados de investigación...
| Comparativa numérico-experimental |
| Fluctuación no estacionaria de presión a la entrada (numérico) | Modos de vibración a la entrada (pto. vista fijo y relativo) |

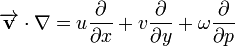
No hay comentarios:
Publicar un comentario