Física

Cinemática

Relación entre las magnitudes angulares y lineales

Magnitudes lineales y angulares

De la definición de radián (unidad natural de medida de ángulos) obtenemos la relación entre el arco y el radio. Como vemos en la figura, el ángulo se obtiene dividiendo la longitud del arco entre su radio

Derivando s=rq  respecto del tiempo, obtenemos la relación entre la velocidad lineal y la velocidad angular

La dirección de la velocidad es tangente a la trayectoria circular, es decir, perpendicular a la dirección radial

Aceleración tangencial

Derivando esta última relación con respecto del tiempo obtenemos la relación entre la aceleración tangencial a_t y la aceleración angular.

Un móvil tiene aceleración tangencial, siempre que el módulo de su velocidad cambie con el tiempo.

Aceleración normal

El cálculo de la componente normal de la aceleración es algo más complicado. La aceleración normal está relacionada con el cambio de la dirección de la velocidad con el tiempo. En un movimiento circular uniforme no existe aceleración tangencial ya que le módulo de la velocidad no cambia con el tiempo, solamente cambia su dirección y por tanto, tiene aceleración normal.

Supongamos un móvil que describe un movimiento circular uniforme.

• En el instante t la velocidad del móvil es v, cuyo módulo es v, y cuya dirección es tangente a la circunferencia.
• En el instante t' la velocidad del móvil v', que tiene el mismo módulo v, pero su dirección ha cambiado.

Calculemos el cambio de velocidad Dv=v’-v que experimenta el móvil entre los instantes t y t', tal como se ve en la figura. El vector Dv tiene dirección radial y sentido hacia el centro de la circunferencia. Los triángulos de color rojo y de color azul de la figura son isósceles y semejantes por lo que podemos establecer la siguiente relación

Donde la cuerda Δs es el módulo del vector desplazamiento entre los instantes t y t'

Dividiendo ambos miembros entre el intervalo de tiempo Dt=t'-t

Cuando el intervalo de tiempo Dt tiende a cero, la cuerda Ds se aproxima al arco, y el cociente ds/dt nos da el módulo de la velocidad v del móvil,

La aceleración normal a_n tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil y su módulo viene dado por una u otra de las expresiones siguientes:

Esta es la deducción más elemental de la fórmula de la aceleración normal que se basa en la identificación de la longitud del arco entre dos puntos de la circunferencia con la cuerda que pasa por dichos puntos, cuando ambos puntos están muy próximos entre sí. Una deducción alternativa se proporciona en la página titulada "Deducción alternativa de las fórmulas de la aceleración tangencial y normal"
Resumiendo

La dirección de la velocidad de un móvil en movimiento circular es tangente a la circunferencia que describe.Un móvil tiene aceleración tangencial at siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera y es de sentido contrario, si se frena. Un móvil que describe un movimiento circular uniforme no tiene aceleración tangencial. Un móvil que describe un movimiento circular siempre tiene aceleración normal, an ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe. La aceleración del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración.

Ejemplo

Una rueda de r=0.1 m de radio está girando con una velocidad de ω₀=4π rad/s, se le aplican los frenos y se detiene en 4s. Calcular

• La aceleración angular

ω=ω₀+αt

En el instante t=4 s la velocidad angular ω=0

α=-π rad/s²

El ángulo girado hasta este instante es

• En el instante t=1 s, la posición y la velocidad angular del móvil es

θ=7π/2=2π+3π/2 rad

ω=4π+(-π)·1=3π rad/s

La velocidad lineal

v=ω·r     v=0.3π m/s

La componente tangencial de la aceleración es at=α·r      at=-0.1π m/s2 La componente normal de la aceleración es an=v2/r    an=0.9π2 m/s2

Movimiento de una bicicleta

Una bicicleta de montaña dispone de tres platos y siete piñones de distinto radio lo que proporciona 21 cambios de marcha al ciclista.
Supondremos que el ciclista hace girar al plato con velocidad angular constante w₁. ¿Cuál es la velocidad v que adquiere el ciclista sobre la bicicleta?.
Supondremos que conocemos los datos relativos a la bicicleta:

• Radio del plato seleccionado, r₁
• Radio del piñón seleccionado, r₂
• Radio de la rueda trasera, r_a
• Radio de la rueda delantera, r_b

Aunque en la mayor parte de las bicicletas los radios de ambas ruedas son iguales, en algunas como las de competición contra-reloj son diferentes como en la simulación más abajo.
La figura representa un plato y un piñón unidos por una cadena. No es necesario saber Cinemática para establecer una relación entre sus respectivas velocidades angulares, y concluir que las velocidades angulares son inversamente proporcionales a sus radios respectivos.

La velocidad de la cadena v_c es la misma que la velocidad de un diente del plato
v_c=w₁·r₁
La velocidad de la cadena v_c es la misma que la velocidad de un diente del piñón
v_c=w₂·r₂
Tenemos de este modo, la relación entre las velocidades angulares w₁ y w₂
w₂·r₂=w₁·r₁
En el tiempo t un eslabón de la cadena se mueve de A a B. Un diente del plato gira un ángulo q₁ y uno del piñón gira un ángulo q₂. Tendremos entonces la siguiente relación
q₂·r₂= q₁·r₁
Ahora nos fijaremos en la rueda trasera. Si suponemos que el piñón es fijo, la velocidad angular del piñón w₂ es la misma que la velocidad angular de la rueda trasera.

De modo que, la velocidad v_a de un punto de la periferia de dicha rueda es
v_a= w₂·r_a
Esta es la velocidad v con que se mueve el ciclista sobre la bicicleta.
En el capítulo sólido rígido estudiaremos con más detalle la relación entre la velocidad de traslación y la velocidad de rotación de un sólido que rueda sin deslizar.
El ángulo girado por dicha rueda en el tiempo t será
q _a== w₂·t
El eje de la rueda delantera está unido al eje de la rueda trasera mediante la estructura rígida de tubos de la bicicleta. La velocidad de traslación de la rueda delantera es la misma que la de la rueda trasera. La velocidad angular de la rueda delantera será
v= w _b·r_b
El ángulo girado por dicha rueda en el tiempo t
q _b= w _b·t

Magnitudes lineales y angulares

De la definición de radián (unidad natural de medida de ángulos) obtenemos la relación entre el arco y el radio. Como vemos en la figura, el ángulo se obtiene dividiendo la longitud del arco entre su radio


Derivando s=rq  respecto del tiempo obtenemos la relación entre la velocidad lineal y la velocidad angular

La dirección de la velocidad es tangente a la trayectoria circular, es decir, perpendicular a la dirección radial

Aceleración tangencial

Derivando esta última relación con respecto del tiempo obtenemos la relación entre la aceleración tangencial a_t y la aceleración angular.

Existe aceleración tangencial, siempre que el módulo de la velocidad cambie con el tiempo, es decir, en un movimiento circular no uniforme.

Aceleración normal

El cálculo de la componente normal de la aceleración es algo más complicado. La aceleración normal está relacionada con el cambio de la dirección de la velocidad con el tiempo. En un movimiento circular uniforme no existe aceleración tangencial ya que le módulo de la velocidad no cambia con el tiempo, solamente cambia su dirección y por tanto, solamente existe aceleración normal.

Supongamos un móvil que describe un movimiento circular uniforme. Calculemos el cambio de velocidad que experimenta el móvil entre los instantes t y t', tal como se ve en la figura. El vector  tiene dirección radial y sentido hacia el centro de la circunferencia. Los triángulos de color rojo y de color azul de la figura son isósceles semejantes por lo que podemos establecer la siguiente relación

Dividiendo ambos miembros entre el intervalo de tiempo Dt=t'-t

Cuando el intervalo de tiempo Dt tiende a cero, la cuerda Ds se aproxima al arco, y el cociente ds/dt nos da la velocidad v del móvil,

La aceleración normal a_n tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil y su módulo viene dado por una u otra de las expresiones siguientes:

La velocidad de un móvil en movimiento circular tiene la dirección tangente a la circunferencia.
Existe aceleración tangencial a_t siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera, y es de sentido contrario si se frena. En un movimiento circular uniforme no hay aceleración tangencial.
En un movimiento circular siempre existe aceleración normal, a_n ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil.
La aceleración total del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración.

Las magnitudes angulares, como su propio nombre indica, están referidas a ángulos. Entre otras cosas nos permiten estudiar los movimientos circulares. En este apartado vamos a presentarte las principales. Veremos:

• Las unidades para medir ángulos: radianes y grados
• La posición angular
• El desplazamiento referido a un ángulo: desplazamiento angular
• Qué es la velocidad angular
• La expresión de la aceleración angular
• Un repaso de la aceleración normal
• La relación que guardan las magnitudes angulares y la lineales
• Una breve introducción a las magnitudes angulares como vectores

Radiánes y Grados

La unidad en el Sistema Internacional (S.I.) para medir ángulos es el radián (rad). Una circunferencia tiene 2π radianes. Por otro lado, podemos medir los ángulos en grados. Una circunferencia tiene 360º. Tenidendo en cuante la relación anterior, para convertir entre grados y radianes puedes utilizar la siguiente expresión:

θgrados=θradianes180π⇔θradianes=θgradosπ180

Ejemplo

Convierte de radianes a grados o grados a radianes los siguientes ángulos:

a) 230º
b) 1.34 rad
 

Ver solución

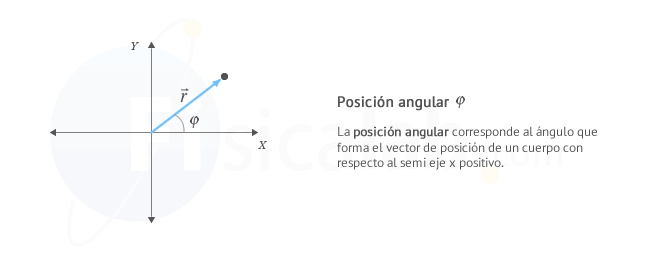
Posición Angular

La posición angular φ es una magnitud angular fundamental que representa el ángulo que forma en cada momento el vector de posición de un cuerpo con el semieje X positivo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el radián (rad).

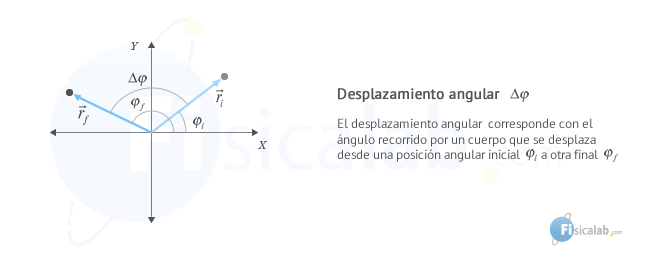
Desplazamiento Angular

El desplazamiento angular (∆φ)  representa el ángulo recorrido. Viene dado por la diferencia entre unaposición angular final φf y una posición angular inicial φi:  

∆φ=φf−φi

Velocidad Angular

Representa el desplazamiento angular (∆φ) experimentado por un cuerpo en cada segundo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el rad/sg aunque en ocasiones verás que se puede utilizar también las revoluciones o vueltas por minuto, r.p.m. (1 r.p.m. = 2π/60 rad/s). Al igual que sucedía con la velocidad, existe la velocidad angular media ωm y la velocidad angular instantánea ω (o simplemente velocidad angular) según se considere un intervalo de tiempo ∆t o un instante de tiempo respectivamente dt.

ωm	ω
ωm=∆φ∆t=φf−φitf−ti	ω=lim∆t→0∆φ∆t=dφdt

Aceleración Angular

Representa la variación de velocidad angular (∆ω) respecto del tiempo. Su unidad en el Sistema Internacional de Unidades (S.I.) es el rad/sg2. Al igual que sucedía con las magnitudes lineales equivalentes, existe la aceleración angular media αm y la aceleración angular instantánea α (o simplemente aceleración angular) según se considere un intervalo de tiempo ∆t o un instante de tiempo respectivamente dt.

αm	α
αm=∆ω∆t=ωf−ωitf−ti	α=lim∆t→0∆ω∆t=dωdt

Aceleración Normal o Centrípeta

Aunque no es una magnitud angular, propiamente dicha, pues no se mide en unidades angulares, es importante recordar aquí la expresión de la aceleración normal o centrípeta.

an=v2R=ω2⋅R

Recuerda que la aceleración normal o centrípeta es la responsable del cambio de dirección del vector velocidad y es por ello que aparece en todos los movimientos circulares.

Relación entre Magnitudes Angulares y Lineales

Podemos relacionar las magnitudes angulares y lineales en los movimientos circulares a través del radio R.

Magnitud Lineal	Relación	Magnitud Angular
s	s=φ⋅R	φ
v	v=ω⋅R	ω
at	at=α⋅R	α
an	an=v2R=ω2⋅R	-

Vectores de Magnitudes Angulares

Hasta ahora hemos estudiado las magnitudes angulares como magnitudes escalares. En realidad, se trata demagnitudes vectoriales pero para los propósitos de este nivel, las consideraremos escalares. No obstante, adelantamos aqui la relacion que guardan la velocidad lineal con la angular y la aceleracion tangencial con la angular, en forma vectorial, que viene dada a traves del producto vectorial:

v⃗ =ω⃗ ×R⃗ 

a⃗ t=α⃗ ×R⃗