Física y química en 3 º de la ESO

La medida, precisión y exactitud

 Instrumentos de medida

La medida directa de las magnitudes se realiza con instrumentos que pueden clasificarse en:

Analógicos: suelen tener un marcador, en muchos casos una aguja, que va girando sobre una escala graduada.

Digitales: el valor de la medida aparece en una pantalla.

2. Precisión y exactitud

Exactitud: un instrumento de medida es tanto más exacto cuanto más se acerquen sus medidas al valor real.

Rango: es el intervalo entre el valor mínimo y máximo que puede medir dicho instrumento.

Fidelidad: un instrumento de medida es tanto más fiel cuanto al realizar varias veces una medida se produzcan los mismos resultados.

3. Error absoluto y error relativo

El error absoluto de una medida es la diferencia entre el valor real de una magnitud y el valor que se ha medido.

Se llama imprecisión absoluta a la media de los errores absolutos tomados todos con signos positivos.

El error relativo de una medida es el cociente entre el error absoluto de la medida y el valor real de ésta.

El error relativo suele expresarse en %.

4. La notación científica

A veces, para expresar números muy grandes o muy pequeños (enteros o decimales), se recurre a la notación científica, que nos permite manejarlos con mayor facilidad.

Un número expresado en notación científica estará formado por un número decimal con una parte entera de una sola cifra distinta de 0, multiplicado por una potencia de 10 de exponente entero.

La exactitud y la precisión son, junto con la incertidumbre, los conceptos más importantes en metrología, con significados diferentes y bien definidos, aunque en el lenguaje de calle se utilicen habitualmente como sinónimos. Así pues, una medición puede ser precisa y, al mismo tiempo, inexacta.

El Vocabulario Internacional de Metrología (VIM) define la precisión como la proximidad entre las indicaciones o valores medidos de un mismo mensurando, obtenidos en mediciones repetidas, bajo condiciones especificadas.

La precisión de una medida suele expresarse numéricamente mediante medidas de dispersión tales como la desviación típica o la varianza. Por ello, cuanto más estrecha sea la distribución de resultados, menor será la desviación típica de la misma y mayor la precisión de la medida. La precisión depende pues únicamente de la distribución de los resultados y no está relacionada con el valor convencionalmente “verdadero” de la medición.

Por su parte, la exactitud viene definida como la proximidad entre el valor medido y el valor “verdadero” del mensurando. Así pues, una medición es más exacta cuanto más pequeño es el error de medida.

Considerando mediciones individuales, la más próxima al valor verdadero será la más exacta. Sin embargo, tras una serie de mediciones repetidas, será la distancia desde el valor medio de la distribución de valores observados, habitualmente el resultado, hasta el valor “verdadero”; es decir el sesgo (valor estimado del error sistemático), la que caracterizará la exactitud de la medición. La dispersión de la distribución de los valores, estimada por su desviación típica, caracterizará, como dijimos antes, la precisión.

Así pues, en mediciones repetidas, la exactitud depende solamente de la posición del valor medio (resultado) de la distribución de valores, no jugando papel alguno en ella la precisión.

Figura 1.

En efecto, observando la Fig. 1 vemos que:

1. La medición individual 1 es más exacta que la medición individual 2, ya que el valor obtenido está más próximo al valor “verdadero”.
2. Cuando se realizan series de mediciones repetidas, solo el valor medio obtenido juega un papel de cara a la exactitud, independientemente de la precisión. Así, el valor medio obtenido en el Caso A es más exacto que el obtenido en el Caso B, por poseer menor sesgo respecto al valor verdadero.

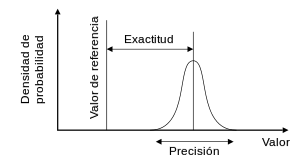
Estos conceptos acostumbran a representarse de forma gráfica acudiendo a la analogía de los disparos sobre una diana, considerando el centro de dicha diana como el valor verdadero o de referencia (Fig. 2).

Así, en el caso 1 de la Fig. 2 se observa una gran dispersión en los disparos, pudiendo asociárseles una distribución uniforme o rectangular. Este hecho refleja falta de precisión, a lo que se añade falta de exactitud, dado el sesgo observado, al encontrarse el valor central de la distribución alejado del valor verdadero. En el caso 2 los disparos están mucho más agrupados, pero el punto medio de todos ellos se encuentra de nuevo alejado del centro de la diana. En este caso, existe buena precisión (los puntos están muy agrupados, sugiriendo una distribución normal o gaussiana), pero falta de exactitud, debido al sesgo (error sistemático) existente entre el valor medio y el valor verdadero (centro de la diana). En el 3^er caso, el valor medio de los disparos coincide con el centro de la diana (buena exactitud), aunque con bastante dispersión (falta de precisión): la distribución es normal en lugar de rectangular. En el último caso, los disparos están muy agrupados en torno al centro de la diana (su distribución de probabilidad es muy estrecha), siendo este el caso ideal de buena precisión y buena exactitud (resultado no sesgado).

Fig. 2: (Arriba) resultados de cuatro series de disparos a un blanco. (Abajo) las correspondientes funciones de densidad de probabilidad.

Tras lo aquí visto podemos concluir que, en efecto, pueden darse todas las combinaciones posibles de exactitud y precisión, siendo compatible la existencia de una de ellas con la falta de la otra. Lo anterior es aplicable tanto a resultados de medida como a los instrumentos utilizados en la obtención de dichos resultados.

http://www.e-medida.es/documentos/Numero-1/exactitud-no-es-lo-mismo-que-precision.htm

Exactitud

La exactitud es lo cerca que el resultado de una medición está del valor verdadero.

Precisión

La precisión es lo cerca que los valores medidos están unos de otros.

Ejemplos de exactitud y precisión:

Exactitud baja Precisión alta	Exactitud alta Precisión baja	Exactitud alta Precisión alta

Así que si estás jugando al fútbol y siempre le das al poste izquierdo en lugar de marcar gol, ¡entonces no eres exacto, pero eres preciso!

Sesgo (¡que no te engañe la precisión!)

Así que si medimos algo varias veces y los valores están cerca unos de otros, pueden estar todos equivocados si hay "sesgo".

Un sesgo es un error sistemático (pasa siempre) que hace que todas las medidas estén desviadas en una cierta cantidad.

Ejemplos de sesgos

• Un balanza dice "1 kg" cuando no hay ningún peso encima
• Siempre mides tu altura con zapatos de suelas anchas
• Un cronómetro que se para medio segundo después de pulsar el botón

Grado de exactitud

La exactitud depende del instrumento de medida. Pero por regla general:

El grado de exactitud es la mitad de la unidad de medida.

Ejemplos:

Si tu instrumento mide en "unidades" entonces cualquier valor entre 6½ y 7½ se mide como "7"
Si tu instrumento mide "de 2 en 2" entonces los valores entre 7 y 9 dan medida "8"

http://www.disfrutalasmatematicas.com/datos/exactitud-precision.html

Precisión se refiere a la dispersión del conjunto de valores obtenidos de mediciones repetidas de una magnitud. Cuanto menor es la dispersión mayor la precisión. Una medida común de la variabilidad es la desviación estándar de las mediciones y la precisión se puede estimar como una función de ella. Es importante resaltar que la automatización de diferentes pruebas o técnicas puede producir un aumento de la precisión. Esto se debe a que con dicha automatización, lo que logramos es una disminución de los errores manuales o su corrección inmediata. No hay que confundir resolución con precisión.

Exactitud se refiere a cuán cerca del valor real se encuentra el valor medido. En términos estadísticos, la exactitud está relacionada con el sesgo de una estimación. Cuanto menor es el sesgo más exacta es una estimación. Cuando se expresa la exactitud de un resultado, se expresa mediante el error absoluto que es la diferencia entre el valor experimental y el valor verdadero.

La exactitud indica los resultados de la proximidad de la medición con respecto al valor verdadero, mientras que la precisión con respecto a la repetibilidad o reproductibilidad de la medida.