MATEMÁTICAS - LISTA DE TEMAS DE ÁLGEBRA ABSTRACTA

homomorfismo es un mapa que preserva la estructura entre dos estructuras algebraicas del mismo tipo (como dos grupos , dos anillos o dos espacios vectoriales ). La palabra homomorfismo proviene de la lengua griega antigua : ὁμός (homos) que significa "igual" y μορφή (morfo) que significa "forma" o "forma". Sin embargo, la palabra aparentemente se introdujo en las matemáticas debido a una (mis) traducción del alemán ähnlich que significa "similar" a ὁμός que significa "igual". ^[1]

Los homomorfismos de los espacios vectoriales también se denominan mapas lineales , y su estudio es el objeto del álgebra lineal .

El concepto de homomorfismo se ha generalizado, bajo el nombre de morfismo , a muchas otras estructuras que, o bien no tienen un conjunto subyacente, o no son algebraicas. Esta generalización es el punto de partida de la teoría de categorías .

Un homomorfismo también puede ser un isomorfismo , un endomorfismo , un automorfismo , etc. (ver más abajo). Cada uno de ellos puede definirse de una manera que puede generalizarse a cualquier clase de morfismos.

Definición [ editar ]

Un homomorfismo es un mapa entre dos estructuras algebraicas del mismo tipo (que es del mismo nombre), que preserva las operaciones de las estructuras. Esto significa un mapa $${\ displaystyle f: A \ to B}entre dos conjuntos A , Bequipado con la misma estructura de modo que, si ∗ es una operación de la estructura (que se supone aquí, para simplificar, que sea una operación binaria ), entonces

$${\ displaystyle f (x * y) = f (x) * f (y)}

para cada par x , y de los elementos de A . ^{[nota 1]} Se dice a menudo que f conserva la operación o es compatible con la operación.

Formalmente, un mapa $${\ displaystyle f: A \ to B}conserva una operación μ de arity k , definida tanto en A como en B si

$${\ displaystyle f (\ mu _ {A} (a_ {1}, \ ldots, a_ {k})) = \ mu _ {B} (f (a_ {1}), \ ldots, f (a_ {k })),}

para todos los elementos de un ₁ , ..., una _k en A .

Las operaciones que deben ser preservadas por un homomorfismo incluyen operaciones 0-arias , que son las constantes. En particular, cuando un elemento de identidad es requerido por el tipo de estructura, el elemento de identidad de la primera estructura debe asignarse al elemento de identidad correspondiente de la segunda estructura.

Por ejemplo:

• Un homomorfismo semigrupo es un mapa entre semigrupos que preserva la operación del semigrupo.
• Un homomorfismo monoide es un mapa entre monoides que conserva la operación monoide y mapea el elemento de identidad del primer monoide al del segundo monoide (el elemento de identidad es una operación 0-aria ).
• Un homomorfismo grupal es un mapa entre grupos que preserva la operación grupal. Esto implica que el homomorfismo de grupo asigna el elemento de identidad del primer grupo al elemento de identidad del segundo grupo, y asigna el inverso de un elemento del primer grupo al inverso de la imagen de este elemento. Por lo tanto, un homomorfismo semigrupo entre grupos es necesariamente un homomorfismo grupal.
• Un homomorfismo en anillo es un mapa entre anillos que preserva la adición del anillo, la multiplicación del anillo y la identidad multiplicativa . La preservación de la identidad multiplicativa depende de la definición de anillo en uso. Si la identidad multiplicativa no se conserva, uno tiene un homomorfismo rng .
• Un mapa lineal es un homomorfismo del espacio vectorial , que es un homomorfismo de grupo entre espacios vectoriales que preserva la estructura de grupo abeliana y la multiplicación escalar .
• Un homomorfismo de módulo , también llamado mapa lineal entre módulos , se define de manera similar.
• Un homomorfismo de álgebra es un mapa que preserva las operaciones de álgebra .

Una estructura algebraica puede tener más de una operación, y se requiere un homomorfismo para preservar cada operación. Por lo tanto, un mapa que conserva solo algunas de las operaciones no es un homomorfismo de la estructura, sino solo un homomorfismo de la subestructura que se obtiene al considerar solo las operaciones preservadas. Por ejemplo, un mapa entre monoides que preserva la operación de monoides y no el elemento de identidad, no es un homomorfismo de monoides, sino solo un homomorfismo semigrupo.

La notación para las operaciones no necesita ser la misma en la fuente y el objetivo de un homomorfismo. Por ejemplo, los números reales forman un grupo para sumar, y los números reales positivos forman un grupo para multiplicación. La función exponencial.

$${\ displaystyle x \ mapsto e ^ {x}}

satisface

$${\ displaystyle e ^ {x + y} = e ^ {x} e ^ {y},}

y es así un homomorfismo entre estos dos grupos. Es incluso un isomorfismo (ver más abajo), ya que su función inversa , el logaritmo natural , satisface

$${\ displaystyle \ ln (xy) = \ ln (x) + \ ln (y),}

Y también es un homomorfismo grupal.

Ejemplos [ editar ]

Monoid homomorfismo f de la monoide ( N , +, 0) a la monoide ( N , ×, 1) , definida por f ( x ) = 2 ^x . Es inyectivo , pero no subjetivo .

Los números reales son un anillo , que tienen tanto la suma como la multiplicación. El conjunto de todas las matrices 2 × 2  también es un anillo, bajo la adición de la matriz y la multiplicación de la matriz . Si definimos una función entre estos anillos de la siguiente manera:

{\ displaystyle f (r) = {\ begin {pmatrix} r & 0 \\ 0 & r \ end {pmatrix}}}

donde r es un número real, entonces f es un homomorfismo de anillos, ya que f conserva ambas sumas:

{\ displaystyle f (r + s) = {\ begin {pmatrix} r + s & 0 \\ 0 & r + s \ end {pmatrix}} = {\ begin {pmatrix} r & 0 \\ 0 & r \ end {pmatrix}} + {\ comience {pmatrix} s & 0 \\ 0 & s \ end {pmatrix}} = f (r) + f (s)}

y multiplicación:

{\ displaystyle f (rs) = {\ begin {pmatrix} rs & 0 \\ 0 & rs \ end {pmatrix}} = {\ begin {pmatrix} r & 0 \\ 0 & r \ end {pmatrix}} {\ begin {pmatrix} s & 0 \\ 0 & s \ end {pmatrix}} = f (r) \, f (s).}

Para otro ejemplo, los números complejos distintos de cero forman un grupo bajo la operación de multiplicación, al igual que los números reales distintos de cero. (El cero debe excluirse de ambos grupos, ya que no tiene un inverso multiplicativo , que se requiere para los elementos de un grupo). Defina una función f de los números complejos distintos de cero a los números reales distintos de cero mediante

$${\ displaystyle f (z) = | z |.}

Es decir, f ( z ) es el valor absoluto (o módulo) del número complejo z . Entonces f es un homomorfismo de grupos, ya que conserva la multiplicación:

$${\ displaystyle f (z_ {1} z_ {2}) = | z_ {1} z_ {2} | = | z_ {1} || z_ {2} | = f (z_ {1}) f (z_ { 2}).}

Tenga en cuenta que f no se puede extender a un homomorfismo de anillos (de los números complejos a los números reales), ya que no conserva la suma:

$${\ displaystyle | z_ {1} + z_ {2} | \ neq | z_ {1} | + | z_ {2} |.}

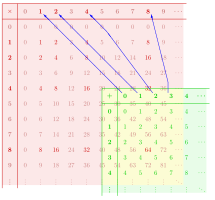
Como otro ejemplo, el diagrama muestra un homomorfismo de monoides f desde el monoide ( N , +, 0) al monoide ( N , ×, 1) . Debido a los diversos nombres de las operaciones correspondientes, las propiedades de la estructura de preservación satisfechas por f cantidad de f ( x + y ) = f ( x ) x f ( y ) y f (0) = 1 .

Una composición álgebra A sobre un campo F tiene una forma cuadrática , llamada una norma , N  : A → F , que es un homomorfismo de grupo desde el grupo multiplicativo de A al grupo multiplicativo de F .

Homomorfismos especiales [ editar ]

Varios tipos de homomorfismos tienen un nombre específico, que también se define para los morfismosgenerales .

Isomorfismo [ editar ]

Un isomorfismo entre estructuras algebraicas del mismo tipo se define comúnmente como un homomorfismo biyectivo . ^{[2] : 134 [3] : 28}

En el contexto más general de la teoría de categorías , un isomorfismo se define como un morfismo , que tiene un inverso que también es un morfismo. En el caso específico de las estructuras algebraicas, las dos definiciones son equivalentes, aunque pueden diferir para las estructuras no algebraicas, que tienen un conjunto subyacente.

Más precisamente, si

$${\ displaystyle f: A \ to B}

Es un (homo) morfismo, tiene un inverso si existe un homomorfismo.

$${\ displaystyle g: B \ a A}

tal que

$${\ displaystyle f \ circ g = \ operatorname {Id} _ {B} \ qquad {\ text {y}} \ qquad g \ circ f = \ operatorname {Id} _ {A}.}

Si A y B tienen conjuntos subyacentes, y$${\ displaystyle f: A \ to B}tiene una inversa g , entonces f es bijetivo. De hecho, f es inyectivo , ya que f ( x ) = f ( y ) implica x = g ( f (x)) = g ( f (y)) = y , y f es supuesta , como, para cualquier xen B , uno tiene x = f ( g ( x )) , y x es la imagen de un elemento deUna .

A la inversa, si $${\ displaystyle f: A \ to B} Es un homomorfismo biyectivo entre estructuras algebraicas, deja $${\ displaystyle g: B \ a A}sea ​​el mapa tal que g ( y ) sea ​​el elemento único x de A tal que f ( x ) = y . Uno tiene$${\ displaystyle f \ circ g = \ operatorname {Id} _ {B} {\ text {y}} g \ circ f = \ operatorname {Id} _ {A},}y solo queda para demostrar que g es un homomorfismo. Si$${\ displaystyle *}es una operación binaria de la estructura, para cada par x , y de elementos de B , uno tiene

$${\ displaystyle g (x * _ {B} y) = g (f (g (x)) * _ {B} f (g (y))) = g (f (g (x) * _ {A} g (y))) = g (x) * _ {A} g (y),}

y g es por lo tanto compatible con$${\ displaystyle *.}Como la prueba es similar para cualquier aridad , esto demuestra que g es un homomorfismo.

Esta prueba no funciona para estructuras no algebraicas. Por ejemplo, para los espacios topológicos , un morfismo es un mapa continuo , y la inversa de un mapa continuo biyectivo no es necesariamente continua. Un isomorfismo de espacios topológicos, llamado homeomorfismo o mapa bicontinuo , es, por lo tanto, un mapa continuo biyectivo, cuyo inverso también es continuo.

Endomorfismo [ editar ]

Un endomorfismo es un homomorfismo cuyo dominio es igual al codominio , o, más generalmente, un morfismocuyo origen es igual al objetivo. ^[2] : 135

Los endomorfismos de una estructura algebraica, o de un objeto de una categoría forman un monoide bajo composición.

Los endomorfismos de un espacio vectorial o de un módulo forman un anillo . En el caso de un espacio vectorial o un módulo libre de dimensión finita , la elección de una base induce un isomorfismo en anillo entre el anillo de endomorfismos y el anillo de matrices cuadradas de la misma dimensión.

Automorfismo [ editar ]

Un automorfismo es un endomorfismo que también es un isomorfismo. ^[2] : 135

Los automorfismos de una estructura algebraica o de un objeto de una categoría forman un grupo en composición, que se denomina grupo de automorfismo de la estructura.

Muchos grupos que han recibido un nombre son grupos de automorfismo de alguna estructura algebraica. Por ejemplo, el grupo lineal general. $${\ displaystyle \ operatorname {GL} _ {n} (k)}es el grupo de automorfismo de un espacio vectorial de dimensión nsobre un campo k .

Los grupos de campos del automorfismo fueron introducidos por Évariste Galois para estudiar las raíces de los polinomios , y son la base de la teoría de Galois .

Monomorfismo [ editar ]

Para las estructuras algebraicas, los monomorfismos se definen comúnmente como homomorfismos inyectivos . ^{[2] : 134 [3] : 29}

En el contexto más general de la teoría de categorías , un monomorfismo se define como un homomorfismo que se puede cancelar . ^[4] Esto significa que un (homo) morfismo$${\ displaystyle f: A \ to B}es un monomorfismo si, para cualquier par g , h de morfismos de cualquier otro objeto C a A , entonces$${\ displaystyle f \ circ g = f \ circ h}implica g = h .

Estas dos definiciones de monomorfismo son equivalentes para todas las estructuras algebraicas comunes. Más precisamente, son equivalentes para campos , para los cuales cada homomorfismo es un monomorfismo, y para variedades de álgebra universal , es decir, estructuras algebraicas para las cuales se definen operaciones y axiomas (identidades) sin ninguna restricción (los campos no son una variedad, como La inversa multiplicativa se define como una operación unaria o como una propiedad de la multiplicación, que, en ambos casos, se define solo para elementos distintos de cero).

En particular, las dos definiciones de un monomorfismo son equivalentes para conjuntos , magmas , semigrupos , monoides , grupos , anillos , campos , espacios vectoriales y módulos .

Un monomorfismo dividido es un homomorfismo que tiene un derecho inverso . Es decir, un homomorfismo.$${\ displaystyle f \ colon A \ to B} Es un homomorfismo dividido si existe un homomorfismo. $${\ displaystyle g \ colon B \ to A} tal que $${\ displaystyle g \ circ f = \ operatorname {Id} _ {A}.}Un monomorfismo dividido es siempre un monomorfismo, para ambos significados de monomorfismo . Para conjuntos y espacios vectoriales, cada monomorfismo es un homomorfismo dividido, pero esta propiedad no es válida para las estructuras algebraicas más comunes.

espectáculoPrueba de la equivalencia de las dos definiciones de monomorfismos.

Epimorfismo [ editar ]

En el álgebra , los epimorfismos a menudo se definen como homomorfismos superyectivos . ^{[2] : 134 [3] : 43} Por otra parte, en la teoría de categorías , los epimorfismos se definen como derechos cancelables . ^[4] Esto significa que un (homo) morfismo$${\ displaystyle f: A \ to B}es un epimorfismo si, para cualquier par g , h de morfismos de B a cualquier otro objeto C , la igualdad$${\ displaystyle g \ circ f = h \ circ f}implica g = h .

Un homomorfismo suprayectivo siempre es cancelable, pero lo contrario no siempre es cierto para las estructuras algebraicas. Sin embargo, las dos definiciones de epimorfismo son equivalentes para conjuntos , espacios vectoriales , grupos abelianos , módulos (ver a continuación una prueba) y grupos . ^[5] La importancia de estas estructuras en todas las matemáticas, y especialmente en el álgebra lineal y el álgebra homológica , puede explicar la coexistencia de dos definiciones no equivalentes.

Las estructuras algebraicas para las cuales existen epimorfismos no subjetivos incluyen semigrupos y anillos . El ejemplo más básico es la inclusión de números enteros en números racionales , que es un homomorfismo de anillos y de semigrupos multiplicativos. Para ambas estructuras es un monomorfismo y un epimorfismo no subjetivo, pero no un isomorfismo. ^[4] [6]

Una amplia generalización de este ejemplo es la localización de un anillo por un conjunto multiplicativo. Cada localización es un epimorfismo de anillo, que no es, en general, un suprayectivo. Como las localizaciones son fundamentales en el álgebra conmutativa y la geometría algebraica , esto puede explicar por qué en estas áreas, la definición de epimorfismos como homomorfismos cancelables de derechos es generalmente la preferida.

Un epimorfismo dividido es un homomorfismo que tiene un inverso a la izquierda . Es decir, un homomorfismo.$${\ displaystyle f \ colon A \ to B} Es un epimorfismo dividido si existe un homomorfismo. $${\ displaystyle g \ colon B \ to A} tal que $${\ displaystyle f \ circ g = \ operatorname {Id} _ {B}.}Un epimorfismo dividido es siempre un epimorfismo, para ambos significados de epimorfismo . Para conjuntos y espacios vectoriales, cada epimorfismo es un epimorfismo dividido, pero esta propiedad no es válida para las estructuras algebraicas más comunes.

En resumen, uno tiene

$${\ displaystyle {\ text {epimorfismo dividido}} \ implica {\ text {epimorfismo (subjetivo)}} \ implica {\ texto {epimorfismo (derecho cancelable)}};}

la última implicación es una equivalencia para conjuntos, espacios vectoriales, módulos y grupos abelianos; La primera implicación es una equivalencia para conjuntos y espacios vectoriales.

espectáculoEquivalencia de las dos definiciones de epimorfismo.

Kernel [ editar ]

Artículo principal: Kernel (álgebra)

Cualquier homomorfismo f  : X → Y define una relación de equivalencia ~ en X por a ~ b si y solo si f ( a ) = f ( b ) . La relación ~ se llama el núcleo de f . Es una relación de congruencia en X . Al conjunto de cocientes X / ~ se le puede dar una estructura del mismo tipo, de manera natural, definiendo las operaciones como [ x ] [y ] = [ x ∗ y ] . En ese caso, la imagen de X en Y bajo el homomorfismo f es necesariamenteisomorfa a X / ~ ; Este hecho es uno de los teoremas de isomorfismo .

Cuando la estructura algebraica es un grupo para alguna operación, la clase de equivalencia K del elemento de identidad de esta operación es suficiente para caracterizar la relación de equivalencia. En este caso, el cociente por la relación de equivalencia se denota por X / K (generalmente se lee como " X mod K "). También en este caso, es K , en lugar de ~ , lo que se llama el núcleo de f. Los núcleos de homomorfismos de un tipo dado de estructura algebraica están naturalmente equipados con alguna estructura. Este tipo de estructura de los núcleos es el mismo que la estructura considerada, en el caso de grupos abelianos , espacios vectoriales y módulos , pero es diferente y ha recibido un nombre específico en otros casos, como subgrupo normal para núcleos de homomorfismos de grupo e ideales para los núcleos de homomorfismos de anillo (en el caso de los anillos no conmutativos, los núcleos son los ideales bilaterales ).

Estructuras relacionales [ editar ]

En la teoría de modelos , la noción de una estructura algebraica se generaliza a estructuras que involucran operaciones y relaciones. Sea L una firma que consta de símbolos de función y relación, y A , B son dos Lestructuras. Entonces, un homomorfismo de A a B es un mapeo h del dominio de A al dominio de B tal que

• h ( F ^A ( a ₁ ,…, a _n )) = F ^B ( h ( a ₁ ),…, h ( a _n )) para cada símbolo de función n en F, en L ,
• R ^A ( un ₁ , ..., un _n ) implica R ^B ( h ( un ₁ ), ..., h ( un _n )) para cada n ary símbolo de relación R en L .

En el caso especial con una sola relación binaria, obtenemos la noción de un homomorfismo gráfico . Para una discusión detallada de homomorfismos relacionales e isomorfismos ver. ^[7]

La teoría del lenguaje formal [ editar ]

Los homomorfismos también se utilizan en el estudio de los lenguajes formales ^[8] y, a menudo, se los denomina morfismos. ^[9] Dados los alfabetos Σ ₁ y Σ ₂ , una función h  : Σ ₁ ^∗ → Σ ₂ ^∗ tal que h ( uv ) = h ( u ) h ( v ) para todos u y v en Σ ₁ ^∗ se llama homomorfismo en Σ ₁ ^∗ . ^{[nota 2]} sih es un homomorfismo en Σ ₁ ^∗ y e denota la palabra vacía, entonces h se llama un homomorfismo sin e cuando h ( x ) ≠ e para todas las x ≠ e en Σ ₁ ^∗ .

El conjunto Σ ^* de las palabras formadas a partir del alfabeto Σ puede ser pensado como el monoide libregenerado por Σ. Aquí la operación monoide es concatenación y el elemento de identidad es la palabra vacía. Desde esta perspectiva, un homormorfismo de lenguaje es precisamente un homomorfismo monoide.

semigrupo es una estructura algebraica que consiste en un conjunto junto con una operación binaria asociativa .

La operación binaria de un semigrupo a menudo se denota multiplicativamente : x · y , o simplemente xy , denota el resultado de aplicar la operación de semigrupo al par ordenado ( x , y ) . La asociatividad se expresa formalmente como que ( x · y ) · z = x · ( y · z ) para todos los x , y y z en el semigrupo.

El nombre "semigrupo" se origina en el hecho de que un semigrupo generaliza un grupo al preservar solo la asociatividad y el cierre bajo la operación binaria de los axiomas que definen un grupo y omite el requisito de un elemento de identidad e inversa. ^{[nota 1]} Desde el punto de vista opuesto (de agregar en lugar de eliminar axiomas ), un semigrupo es un magma asociativo . Como en el caso de grupos o magmas, la operación del semigrupo no necesita ser conmutativa , por lo que x · y no es necesariamente igual a y · x ; Un ejemplo típico de operación asociativa pero no conmutativa esmultiplicación de matrices . Si la operación del semigrupo es conmutativa, entonces el semigrupo se denomina semigrupo conmutativo o (con menos frecuencia que en el caso análogo de grupos ) puede denominarse semigrupo abeliano .

Un monoide es una estructura algebraica intermedia entre grupos y semigrupos, y es un semigrupo que tiene un elemento de identidad , por lo que obedece a todos menos uno de los axiomas de un grupo; No se requiere la existencia de inversos de un monoide. Un ejemplo natural son las cadenas con concatenación como operación binaria y la cadena vacía como elemento de identidad. La restricción a cadenas no vacías da un ejemplo de un semigrupo que no es un monoide. Los enteros positivos con suma forman un semigrupo conmutativo que no es un monoide, mientras que los enteros no negativoshacer un monoide. Un semigrupo sin un elemento de identidad se puede convertir fácilmente en un monoide simplemente agregando un elemento de identidad. En consecuencia, los monoides se estudian en la teoría de los semigrupos en lugar de en la teoría de grupos. Los semigrupos no deben confundirse con los cuasigrupos , que son una generalización de grupos en una dirección diferente; la operación en un quasigroup no necesita ser asociativa, pero los quasigroups conservan de los grupos una noción de división . La división en semigrupos (o en monoides) no es posible en general.

El estudio formal de los semigrupos comenzó a principios del siglo XX. Los primeros resultados incluyen un teorema de Cayley para semigrupos que realizan cualquier semigrupo como semigrupo de transformación , en el que las funciones arbitrarias reemplazan el papel de las biecciones de la teoría de grupos. Sin embargo, otras técnicas fundamentales de estudiar semigrupos como las relaciones de Green no imitan nada en la teoría de grupos. Un resultado profundo en la clasificación de semigrupos finitos es la teoría de Krohn-Rhodes . La teoría de los semigrupos finitos ha sido de particular importancia en la informática teórica desde la década de 1950 debido al vínculo natural entre los semigrupos finitos y los autómatas finitos a través del monoide sintáctico.. En la teoría de la probabilidad , los semigrupos están asociados con los procesos de Markov . ^[1] [2] En otras áreas de las matemáticas aplicadas , los semigrupos son modelos fundamentales para sistemas lineales invariantes en el tiempo . En las ecuaciones diferenciales parciales , un semigrupo está asociado a cualquier ecuación cuya evolución espacial es independiente del tiempo. Existen numerosas clases especiales de semigrupos , semigrupos con propiedades adicionales, que aparecen en aplicaciones particulares. Algunas de estas clases están aún más cerca de los grupos al exhibir algunas propiedades adicionales de un grupo, pero no todas. De estos mencionamos: semigrupos regulares ,Semigrupos ortodoxos , semigrupos con involución , semigrupos inversos y semigrupos cancelativos . También hay clases interesantes de semigrupos que no contienen ningún grupo, excepto el grupo trivial ; Ejemplos de este último tipo son las bandas y su subclase conmutativa: semilattices , que también son estructuras algebraicas ordenadas .

Definición [ editar ]

Un semigrupo es un conjunto. $${\ displaystyle S}junto con una operación binaria "$${\ displaystyle \ cdot}"(es decir, una función $${\ displaystyle \ cdot: S \ times S \ rightarrow S}) que satisface la propiedad asociativa :

Para todos $${\ displaystyle a, b, c \ en S}, la ecuacion $${\ displaystyle (a \ cdot b) \ cdot c = a \ cdot (b \ cdot c)} sostiene

Más sucintamente, un semigrupo es un magma asociativo .

Ejemplos de semigrupos [ editar ]

• Semigroup vacío : el conjunto vacío forma un semigroup con la función vacía como la operación binaria.
• Semigrupo con un elemento : esencialmente hay solo uno (específicamente, solo uno hasta isomorfismo ), el singleton { a } con la operación a · a = a .
• Semigrupo con dos elementos : hay cinco que son esencialmente diferentes.
• El conjunto de enteros positivos con la suma. (Con 0 incluido, esto se convierte en un monoide ).
• El conjunto de enteros con mínimo o máximo. (Con el infinito positivo / negativo incluido, esto se convierte en un monoide).
• Matrices cuadradas no negativas de un tamaño dado con multiplicación de matrices.
• Cualquier ideal de un anillo con la multiplicación del anillo.
• El conjunto de todas las cadenas finitas sobre un alfabeto fijo Σ con concatenación de cadenas como operación de semigrupo, el llamado " semigrupo libre sobre Σ". Con la cadena vacía incluida, este semigrupo se convierte en el monoide libre sobre Σ.
• Una distribución de probabilidad F junto con todas las potencias de convolución de F, con convolución como la operación. Esto se llama un semigrupo de convolución.
• Un monoide es un semigrupo con un elemento de identidad .
• Un grupo es un monoide en el que cada elemento tiene un elemento inverso .
• Semigrupos de transformación y monoides .
• El conjunto de funciones continuas de un espacio topológico a sí mismo con composición de funciones forma un monoide con la función de identidad actuando como la identidad. Más en general, los endomorfismos de cualquier objeto de una categoría forman un monoide en composición.

Conceptos básicos [ editar ]

Identidad y cero [ editar ]

Una identidad izquierda de un semigrupo.$${\ displaystyle S}(o más en general, el magma ) es un elemento$${\ displaystyle e} tal que para todos $${\ displaystyle x} en $${\ displaystyle S}, $${\ displaystyle ex = x}. Del mismo modo, una identidad correcta es un elemento.$${\ displaystyle f} tal que para todos $${\ displaystyle x} en $${\ displaystyle S}, $${\ displaystyle xf = x}. Las identidades izquierda y derecha se denominan identidades unilaterales . Un semigrupo puede tener una o más identidades a la izquierda pero no una identidad a la derecha, y viceversa.

Una identidad de dos lados (o simplemente identidad ) es un elemento que es tanto una identidad izquierda como una derecha. Los semigrupos con una identidad de dos caras se llaman monoides . Un semigrupo puede tener a lo sumo una identidad de dos caras. Si un semigrupo tiene una identidad de dos lados, entonces la identidad de dos lados es la única identidad de un solo lado en el semigrupo. Si un semigrupo tiene una identidad izquierda y una identidad derecha, entonces tiene una identidad de dos caras (que por lo tanto es la identidad única de una cara).

Un semigrupo $${\ displaystyle S}sin identidad se puede incrustar en un monoide formado por un elemento adyacente$${\ displaystyle e \ notin S} a $${\ displaystyle S} y definiendo $${\ displaystyle e \ cdot s = s \ cdot e = s} para todos $${\ displaystyle s \ en S \ cup \ {e \}}. ^[3] [4] La notación$${\ displaystyle S ^ {1}} denota un monoide obtenido de $${\ displaystyle S}adjuntando una identidad si es necesario ($${\ displaystyle S ^ {1} = S}para un monoide). ^[4]

De manera similar, cada magma tiene a lo sumo un elemento absorbente , que en teoría de semigrupos se denomina cero . Análogamente a la construcción anterior, para cada semigrupo$${\ displaystyle S}, se puede definir $${\ displaystyle S ^ {0}}, un semigrupo con 0 que incrusta $${\ displaystyle S}.

Subgrupos e ideales [ editar ]

La operación de semigrupo induce una operación en la colección de sus subconjuntos: dados los subconjuntos Ay B de un semigrupo S , su producto A · B , escrito comúnmente como AB , es el conjunto { ab | a en A y b en B }. (Esta noción se define de forma idéntica a los grupos ). En términos de esta operación, se llama un subconjunto A

• un sub-grupo si AA es un subconjunto de A ,
• un ideal correcto si AS es un subconjunto de A , y
• un ideal a izquierda si SA es un subconjunto de A .

Si A es tanto un ideal de izquierda como un ideal de derecha, entonces se llama ideal (o ideal de dos caras ).

Si S es un semigrupo, entonces la intersección de cualquier colección de subsemigroups de S es también un subsemigroup de S . Así que los subgrupos de S forman una red completa .

Un ejemplo de semigrupo sin ideal mínimo es el conjunto de enteros positivos que se suman. El ideal mínimo de un semigrupo conmutativo , cuando existe, es un grupo.

Las relaciones de Green , un conjunto de cinco relaciones de equivalencia que caracterizan a los elementos en términos de los ideales principales que generan, son herramientas importantes para analizar los ideales de un semigrupo y las nociones relacionadas de estructura.

El subconjunto con la propiedad que todos sus elementos conmuta con cualquier otro elemento del semigrupo se denomina el centro del semigrupo. ^[5] El centro de un semigrupo es en realidad un subgrupo. ^[6]

Homomorfismos y congruencias [ editar ]

Un homomorfismo semigrupo es una función que preserva la estructura de semigrupos. Una función f : S → Tentre dos semigrupos es un homomorfismo si la ecuación

f ( ab ) = f ( a ) f ( b ) .

se mantiene para todos los elementos a , b en S , es decir, el resultado es el mismo cuando se realiza la operación de semigrupo después o antes de aplicar el mapa f .

Un homomorfismo semigrupo entre monoides conserva la identidad si se trata de un homomorfismo monoide . Pero hay homomorfismos semigrupos que no son homomorfismos monoides, por ejemplo, la inclusión canónica de un semigrupo$${\ displaystyle S} sin identidad en $${\ displaystyle S ^ {1}}. Las condiciones que caracterizan los homomorfismos monoides se discuten más a fondo. Dejar$${\ displaystyle f: S_ {0} \ a S_ {1}}Ser un homomorfismo semigrupo. La imagen de$${\ displaystyle f}También es un semigrupo. Si$${\ displaystyle S_ {0}} Es un monoide con un elemento de identidad. $${\ displaystyle e_ {0}}, entonces $${\ displaystyle f (e_ {0})} Es el elemento de identidad en la imagen de. $${\ displaystyle f}. Si$${\ displaystyle S_ {1}} También es un monoide con un elemento de identidad. $${\ displaystyle e_ {1}} y $${\ displaystyle e_ {1}} pertenece a la imagen de $${\ displaystyle f}, entonces $${\ displaystyle f (e_ {0}) = e_ {1}}es decir $${\ displaystyle f}Es un homomorfismo monoide. En particular, si$${\ displaystyle f}Es suryectivo , entonces es un homomorfismo monoide.

Se dice que dos semigrupos S y T son isomorfos si hay una bijection f  : S ↔ T con la propiedad de que, para cualquier elemento a , b en S , f ( ab ) = f ( a ) f ( b ) . Los semigrupos isomorfos tienen la misma estructura.

Una congruencia semigrupo $${\ displaystyle \ sim}es una relación de equivalencia que es compatible con la operación de semigrupo. Es decir, un subconjunto.$${\ displaystyle \ sim \; \ subseteq S \ times S} Esa es una relación de equivalencia y $${\ displaystyle x \ sim y \,} y $${\ displaystyle u \ sim v \,} implica $${\ displaystyle xu \ sim yv \,} para cada $${\ displaystyle x, y, u, v}en s . Como cualquier relación de equivalencia, una congruencia de semigrupos.$${\ displaystyle \ sim}induce clases de congruencia

$${\ displaystyle [a] _ {\ sim} = \ {x \ en S \ vert \; x \ sim a \}}

y la operación semigrupo induce una operación binaria $${\ displaystyle \ circ} en las clases de congruencia:

$${\ displaystyle [u] _ {\ sim} \ circ [v] _ {\ sim} = [uv] _ {\ sim}}

Porque $${\ displaystyle \ sim} es una congruencia, el conjunto de todas las clases de congruencia de $${\ displaystyle \ sim} forma un semigrupo con $${\ displaystyle \ circ}, llamado cociente semigrupo o factor semigrupo , y se denota$${\ displaystyle S / \ sim}. El mapeo$${\ displaystyle x \ mapsto [x] _ {\ sim}}es un homomorfismo semigrupo, llamada la aplicación cociente , canónica surjection o de proyección ; si S es un monoide, el semigrupo cociente es un monoide con identidad$${\ displaystyle [1] _ {\ sim}}. Por el contrario, el núcleo de cualquier homomorfismo semigrupo es una congruencia semigrupo. Estos resultados no son más que una particularización del primer teorema de isomorfismo en el álgebra universal . Las clases de congruencia y los monoides de factor son los objetos de estudio en los sistemas de reescritura de cadenas .

Una congruencia nuclear en S es uno que es el núcleo de un endomorfismo de S . ^[7]

Un semigrupo S satisface la condición máxima en congruencias si alguna familia de congruencias en S , ordenada por inclusión, tiene un elemento máximo. Por el Lema de Zorn , esto es equivalente a decir que la condición de cadena ascendente sostiene: no hay una infinita cadena estrictamente ascendente de congruencias en S . ^[8]

Cada ideales I de un semigrupo induce una subsemigroup, el factor de semigrupo Rees a través de la congruencia x ρ y   ⇔ o bien x = y o ambos x y y están en I .

Cocientes y divisiones [ editar ]

Las siguientes nociones ^[9] introducen la idea de que un semigrupo está contenido en otro.

Un semigrupo T es un cociente de un semigrupo S si hay un morfismo semigrupo sobreyectiva de S a T . Por ejemplo,$${\ displaystyle (\ mathbb {Z} / 2 \ mathbb {Z}, +)} es un cociente de $${\ displaystyle (\ mathbb {Z} / 4 \ mathbb {Z}, +)}, usando el morfismo que consiste en tomar el resto módulo pde un número entero.

Un semigrupo T divide un semigrupo S , anotado$${\ displaystyle T \ preceq S}si T es un cociente de un subsemigroup S . En particular, subsemigroups de S divide T , mientras que no es necesariamente el caso que hay un cociente de S .

Ambas relaciones son transitivas.

Estructura de semigrupos [ editar ]

Para cualquier subconjunto A de S hay un pequeño subsemigroup T de S que contiene A , y decimos que A genera T . Un solo elemento x de S genera el subgrupo { x ⁿ | n es un entero positivo}. Si esto es finito, entonces se dice que x es de orden finito , de lo contrario es de orden infinito . Se dice que un semigrupo es periódicoSi todos sus elementos son de orden finito. Un semigrupo generado por un solo elemento se dice que es monogénico (o cíclico ). Si un semigrupo monogénico es infinito, entonces es isomorfo al semigrupo de enterospositivos con la operación de adición. Si es finito y no vacío, debe contener al menos un idempotente . Se deduce que cada semigrupo periódico no vacío tiene al menos un idempotente.

Un subgrupo que también es un grupo se llama subgrupo . Existe una estrecha relación entre los subgrupos de un semigrupo y sus idempotents. Cada subgrupo contiene exactamente un idempotente, a saber, el elemento de identidad del subgrupo. Para cada idempotente e del semigrupo hay un único subgrupo máximo que contiene e . Cada subgrupo máximo surge de esta manera, por lo que hay una correspondencia de uno a uno entre idempotentes y subgrupos máximos. Aquí el término subgrupo máximo difiere de su uso estándar en la teoría de grupos.

A menudo se puede decir más cuando el orden es finito. Por ejemplo, cada semigrupo finito no vacío es periódico y tiene un ideal mínimo y al menos un idempotente. El número de semigrupos finitos de un tamaño dado (mayor que 1) es (obviamente) mayor que el número de grupos del mismo tamaño. Por ejemplo, de las dieciséis posibles "tablas de multiplicación" para un conjunto de dos elementos {a, b}, ocho semigrupos forman ^{[nota 2],} mientras que solo cuatro de estos son monoides y solo dos grupos forman. Para obtener más información sobre la estructura de los semigrupos finitos, consulte la teoría de Krohn-Rhodes .