MATEMÁTICAS - LISTA DE TEMAS DE ÁLGEBRA ABSTRACTA

Un diagrama utilizado en el lema de la serpiente , un resultado básico en el álgebra homológica.

El álgebra homológica es la rama de las matemáticas que estudia la homología en un entorno algebraico general. Es una disciplina relativamente joven, cuyos orígenes se pueden remontar a investigaciones en topología combinatoria (un precursor de la topología algebraica ) y álgebra abstracta (teoría de módulosy sicigias ) a finales del siglo XIX, principalmente por Henri Poincaré y David Hilbert .

El desarrollo del álgebra homológica estuvo estrechamente relacionado con el surgimiento de la teoría de categorías . En general, el álgebra homológica es el estudio de los funtores homológicos y las intrincadas estructuras algebraicas que conllevan. Un concepto bastante útil y ubicuo en matemáticas es el de los complejos de cadenas , que pueden ser estudiados a través de su homología y cohomología . El álgebra homológica proporciona los medios para extraer información contenida en estos complejos y presentarla en forma de invariantes homológicos de anillos , módulos, espacios topológicos y otros objetos matemáticos "tangibles". Una poderosa herramienta para hacer esto es proporcionada porSecuencias espectrales .

Desde sus orígenes, el álgebra homológica ha desempeñado un papel enorme en la topología algebraica. Su influencia se ha expandido gradualmente y actualmente incluye álgebra conmutativa , geometría algebraica , la teoría de números algebraica , teoría de la representación , la física matemática , álgebra de operadores , análisis complejo , y la teoría de ecuaciones diferenciales parciales . La teoría K es una disciplina independiente que se basa en métodos de álgebra homológica, al igual que la geometría no conmutativa de Alain Connes .

La historia del álgebra homológica [ editar ]

El álgebra homológica comenzó a ser estudiada en su forma más básica en la década de 1800 como una rama de la topología, pero no fue hasta la década de 1940 que se convirtió en un tema independiente con el estudio de objetos como el extorsor y el tortor , entre otros. otros. ^[1]

Complejos de la cadena y la homología [ editar ]

Artículo principal: Complejo de cadenas.

La noción de complejo de cadenas es central en el álgebra homológica. Un complejo de cadenas abstractas es una secuencia.$${\ displaystyle (C _ {\ bullet}, d _ {\ bullet})}de grupos abelianos y homomorfismos de grupo , con la propiedad de que la composición de dos mapas consecutivos cualquiera es cero:

${\displaystyle C_{\bullet }:\cdots \longrightarrow C_{n+1}{\stackrel {d_{n+1}}{\longrightarrow }}C_{n}{\stackrel {d_{n}}{\longrightarrow }}C_{n-1}{\stackrel {d_{n-1}}{\longrightarrow }}\cdots ,\quad d_{n}\circ d_{n+1}=0.}$

Los elementos de C _n se llaman n - cadenas y los homomorfismos d _n son llamados los mapas de los límites o diferenciales . Los grupos de cadenas C _n pueden estar dotados de estructura adicional; por ejemplo, pueden ser espacios vectoriales o módulos de más de un fijo anillo R . Los diferenciales deben preservar la estructura extra si existe; por ejemplo, deben ser mapas lineales u homomorfismos de los módulos R. Para mayor comodidad de notación, restrinja la atención a los grupos abelianos (más correctamente, a lacategoría ab de grupos abelianos); un famoso teorema de Barry Mitchell implica que los resultados se generalizarán a cualquier categoría abeliana . Cada complejo de cadena define dos secuencias adicionales de grupos abelianos, los ciclos Z _n  = Ker d _n y los límites B _n  = Im d _n +1 , donde Ker  d e Im  d denotan el núcleo y la imagen de d . Dado que la composición de dos mapas de límites consecutivos es cero, estos grupos se integran entre sí como

$${\ displaystyle B_ {n} \ subseteq Z_ {n} \ subseteq C_ {n}.}

Los subgrupos de grupos abelianos son automáticamente normales ; por lo tanto, podemos definir el n º homología grupo H _n ( C ) como el grupo de factor de los n -cycles por los n -boundaries,

$${\ displaystyle H_ {n} (C) = Z_ {n} / B_ {n} = \ operatorname {Ker} \, d_ {n} / \ operatorname {Im} \, d_ {n + 1}.}

Un complejo de cadenas se denomina secuencia acíclica o exacta si todos sus grupos de homología son cero.

Los complejos de cadenas surgen en abundancia en álgebra y topología algebraica . Por ejemplo, si X es un espacio topológico, entonces las cadenas singulares C _n ( X ) son combinaciones lineales formales de mapas continuos del estándar n - simplex a X ; si K es un complejo simplicial, entonces las cadenas simpliciales C _n ( K ) son combinaciones lineales formales de los n -simplices de K ; SiA  =  F / R es una presentación de un grupo abeliano A por generadores y relaciones , donde F es un grupo abeliano libre abarcado por los generadores y Res el subgrupo de relaciones, dejando que C ₁ ( A ) =  R , C ₀ ( A ) =  F , y C _n ( A ) = 0 para todos los demás ndefine una secuencia de grupos abelianos. En todos estos casos, existen diferencias naturales d _n toma C _n en un complejo de la cadena, cuya homología refleja la estructura del espacio topológico X , el complejo simplicial K, o el grupo abeliano A . En el caso de los espacios topológicos, llegamos a la noción de homología singular , que desempeña un papel fundamental en la investigación de las propiedades de dichos espacios, por ejemplo, múltiples .

A nivel filosófico, el álgebra homológica nos enseña que ciertos complejos de cadenas asociados con objetos algebraicos o geométricos (espacios topológicos, complejos simpliciales, módulos R ) contienen una gran cantidad de información algebraica valiosa sobre ellos, siendo la homología solo la parte más fácilmente disponible. . A nivel técnico, el álgebra homológica proporciona las herramientas para manipular complejos y extraer esta información. Aquí hay dos ilustraciones generales.

• Dos objetos X e Y están conectados por un mapa f entre ellos. El álgebra homológica estudia la relación, inducida por el mapa f , entre los complejos de cadenas asociados con X e Y y su homología. Esto se generaliza al caso de varios objetos y mapas que los conectan. Fraseado en el lenguaje de la teoría de categorías , el álgebra homológica estudia las propiedades funcionales de varias construcciones de complejos de cadenas y la homología de estos complejos.
• Un objeto X admite múltiples descripciones (por ejemplo, como un espacio topológico y como un complejo de simplicidad) o el complejo$${\ displaystyle C _ {\ bullet} (X)}se construye utilizando alguna 'presentación' de X , que implica elecciones no canónicas. Es importante conocer el efecto del cambio en la descripción de X en complejos de la cadena asociados con X . Típicamente, el complejo y su homología. $${\ displaystyle H _ {\ bullet} (C)}Son funcionales con respecto a la presentación; y la homología (aunque no el complejo en sí) es realmente independiente de la presentación elegido, por lo que es una invariante de X .

Herramientas estandar [ editar ]

Secuencias exactas [ editar ]

Artículo principal: secuencia exacta

En el contexto de la teoría de grupos , una secuencia.

$${\ displaystyle G_ {0} \; {\ xrightarrow {f_ {1}}} \; G_ {1} \; {\ xrightarrow {f_ {2}}} \; G_ {2} \; {\ xrightarrow {f_ {3}}} \; \ cdots \; {\ xrightarrow {f_ {n}}} \; G_ {n}}

de grupos y homomorfismos de grupo se llama exacto si la imagen (o rango ) de cada homomorfismo es igual al núcleo del siguiente:

$${\ displaystyle \ mathrm {im} (f_ {k}) = \ mathrm {ker} (f_ {k + 1}). \!}

Tenga en cuenta que la secuencia de grupos y homomorfismos puede ser finita o infinita.

Se puede hacer una definición similar para ciertas otras estructuras algebraicas . Por ejemplo, uno podría tener una secuencia exacta de espacios vectoriales y mapas lineales , o de módulos y homomorfismos de módulos . De manera más general, la noción de una secuencia exacta tiene sentido en cualquier categoría con núcleos y núcleos .

Secuencia exacta corta [ editar ]

El tipo más común de secuencia exacta es la secuencia exacta corta . Esta es una secuencia exacta de la forma.

$${\ displaystyle A \; {\ overset {f} {\ hookrightarrow}}; B \; {\ overset {g} {\ twoheadrightarrow}} \; C}

donde ƒ es una monomorphism y g es un epimorfismo . En este caso, A es un subobjeto de B , y el cocientecorrespondiente es isomorfo a C :

$${\ displaystyle C \ cong B / f (A).}

(donde f (A) = im ( f )).

Una secuencia exacta corta de grupos abelianos también se puede escribir como una secuencia exacta con cinco términos:

$${\ displaystyle 0 \; {\ xrightarrow {}} \; A \; {\ xrightarrow {f}} \; B \; {\ xrightarrow {g}} \; C \; {\ xrightarrow {}} \; 0 }

donde 0 representa el objeto cero , como el grupo trivial o un espacio vectorial de dimensión cero. La colocación de las fuerzas de 0 para ser un monomorfismo yg para ser un epimorfismo (ver más abajo).

Secuencia exacta larga [ editar ]

Una secuencia exacta larga es una secuencia exacta indexada por los números naturales .

Los cinco lemas [ editar ]

Artículo principal: Cinco lemma.

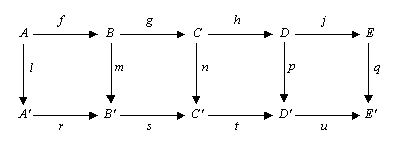
Considere el siguiente diagrama conmutativo en cualquier categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un campo determinado ) o en la categoría de grupos .

El lema de los cinco establece que, si las filas son exacta , m y p son isomorfismos , l es un epimorfismo , y q es un monomorphism , entonces n también es un isomorfismo.

La serpiente lema [ editar ]

Artículo principal: lemma serpiente

En una categoría abeliana (como la categoría de grupos abelianos o la categoría de espacios vectoriales sobre un campo determinado ), considere un diagrama conmutativo :

donde las filas son secuencias exactas y 0 es el objeto cero . Luego hay una secuencia exacta que relaciona los núcleos y cokernels de a , b , y c :

$${\ displaystyle \ ker a \ to \ ker b \ to \ ker c {\ overset {d} {\ to}} \ operatorname {coker} a \ to \ operatorname {coker} b \ to \ operatorname {coker} c}

Además, si el morfismo f es un monomorfismo , entonces también lo es el morfismo ker  a → ker  b , y si g ' es un epimorfismo , entonces también lo es coker  b → coker  c .

Categorías abelianas [ editar ]

Artículo principal: categoría abeliana.

En matemáticas , una categoría abeliana es una categoría en la que se pueden agregar morfismos y objetos y en la que existen núcleos y pepinos y tienen propiedades deseables. El ejemplo de prototipo motivador de una categoría abeliana es la categoría de grupos abelianos , Ab . La teoría se originó en un intento tentativo de unificar varias teorías de cohomología por Alexander Grothendieck . Las categorías abelianas son categorías muy estables , por ejemplo, son regulares y satisfacen el lema de la serpiente. La clase de categorías abelianas está cerrada bajo varias construcciones categóricas, por ejemplo, la categoría de complejos de cadena de una categoría abeliana, o la categoría de functores de una categoría pequeña a una categoría abeliana también son abelianas. Estas propiedades de estabilidad las hacen inevitables en el álgebra homológica y más allá; La teoría tiene aplicaciones principales en geometría algebraica , cohomología y teoría de categorías puras . Las categorías abelianas llevan el nombre de Niels Henrik Abel .

Más concretamente, una categoría es abeliana si

• tiene un objeto cero ,
• Tiene todos los productos binarios y coproductos binarios , y
• Tiene todos los núcleos y cokernels .
• Todos los monomorfismos y epimorfismos son normales .

El functor ext [ editar ]

Artículo principal: ext.

Deje que R sea un anillo y dejar Mod _R sea la categoría de módulos de más de R . Deje que B sea en Mod _R y establece T ( B ) = Hom _R ( A, B ), para fija A en Mod _R . Este es un funtor exacto izquierda y por lo tanto ha derecho derivado funtores R ⁿ T . El functor ext está definido por

$${\ displaystyle \ operatorname {Ext} _ {R} ^ {n} (A, B) = (R ^ {n} T) (B).}

Esto se puede calcular tomando cualquier resolución inyectiva.

$${\ displaystyle 0 \ rightarrow B \ rightarrow I ^ {0} \ rightarrow I ^ {1} \ rightarrow \ dots,}

y computacion

$${\ displaystyle 0 \ rightarrow \ operatorname {Hom} _ {R} (A, I ^ {0}) \ rightarrow \ operatorname {Hom} _ {R} (A, I ^ {1}) \ rightarrow \ dots.}

Entonces ( R ⁿ T ) ( B ) es la homología de este complejo. Tenga en cuenta que Hom _R ( A, B ) está excluido del complejo.

Una definición alternativa se da usando el functor G ( A ) = Hom _R ( A, B ). Para un módulo B fijo , este es un funtor exacto izquierdo contravariante , por lo que también tenemos los funtores derivados a la derecha R ⁿ G , y podemos definir

$${\ displaystyle \ operatorname {Ext} _ {R} ^ {n} (A, B) = (R ^ {n} G) (A).}

Esto se puede calcular eligiendo cualquier resolución proyectiva.

$${\ displaystyle \ dots \ rightarrow P ^ {1} \ rightarrow P ^ {0} \ rightarrow A \ rightarrow 0,}

y procediendo dualmente por computación

$${\ displaystyle 0 \ rightarrow \ operatorname {Hom} _ {R} (P ^ {0}, B) \ rightarrow \ operatorname {Hom} _ {R} (P ^ {1}, B) \ rightarrow \ dots.}

Entonces ( R ⁿ G ) ( A ) es la homología de este complejo. Tenga en cuenta nuevamente que Hom _R ( A, B ) está excluido.

Estas dos construcciones producen resultados isomorfos , por lo que ambas pueden usarse para calcular el functor Ext.

Tor functor [ editar ]

Artículo principal: Tor functor

Supongamos que R es un anillo , y denota por R - Mod la categoría de la izquierda R -modules y por Mod - R de la categoría de la derecha R -modules (si R es conmutativo , las dos categorías coinciden). Fijar un módulo B en R - Mod . Para A en Mod - R , ajuste T ( A ) = A ⊗ _R B . Entonces tes un funtor exacto correcto de Mod - R a la categoría de los grupos abelianos Ab (en el caso de que R sea ​​conmutativo, es un funtor exacto correcto de Mod- R a Mod - R ) y sus funtores derivados izquierdos L _n T están definidos . Nosotros fijamos

$${\ displaystyle \ mathrm {Tor} _ {n} ^ {R} (A, B) = (L_ {n} T) (A)}

Es decir, tomamos una resolución proyectiva.

$${\ displaystyle \ cdots \ rightarrow P_ {2} \ rightarrow P_ {1} \ rightarrow P_ {0} \ rightarrow A \ rightarrow 0}

luego elimine el término A y tense la resolución proyectiva con B para obtener el complejo

$${\ displaystyle \ cdots \ rightarrow P_ {2} \ otimes _ {R} B \ rightarrow P_ {1} \ otimes _ {R} B \ rightarrow P_ {0} \ otimes _ {R} B \ rightarrow 0}

(tenga en cuenta que A ⊗ _R B no aparece y la última flecha es solo el mapa cero) y tome la homología de este complejo.

Secuencia espectral [ editar ]

Artículo principal: Secuencia espectral

Corrija una categoría abeliana , como una categoría de módulos sobre un anillo. Una secuencia espectral es una elección de un entero no negativo r ₀ y una colección de tres secuencias:

1. Para todos los enteros r ≥ r ₀ , un objeto E _r , llamado hoja (como en una hoja de papel ), oa veces una página o un término ,
2. Endomorfismos d _r  : E _r → E _{r que} satisfacen d _r o d _r = 0, llamados mapas de límites o diferenciales ,
3. Isomorfismos de E _{r + 1} con H ( E _r ), la homología de E _r con respecto a d _r .

La hoja E ₂ de una secuencia espectral cohomológica.

Una secuencia espectral de doble graduación tiene una gran cantidad de datos de los que se debe realizar un seguimiento, pero existe una técnica de visualización común que hace que la estructura de la secuencia espectral sea más clara. Tenemos tres índices, r , p , y q . Para cada r , imagina que tenemos una hoja de papel cuadriculado. En esta hoja, tomaremos p para ser la dirección horizontal yq para ser la dirección vertical. En cada punto de la red tenemos el objeto.$${\ displaystyle E_ {r} ^ {p, q}}.

Es muy común que n = p + q sea ​​otro índice natural en la secuencia espectral. n corre diagonalmente, de noroeste a sureste, a través de cada hoja. En el caso homológico, los diferenciales tienen grado de bipedestación (- r ,  r  - 1), por lo que disminuyen n en uno. En el caso cohomológico, n se incrementa en uno. Cuando r es cero, el diferencial mueve los objetos un espacio hacia arriba o hacia abajo. Esto es similar al diferencial en un complejo de cadenas. Cuando r es uno, el diferencial mueve los objetos un espacio hacia la izquierda o hacia la derecha. Cuando res dos, el diferencial mueve objetos como el movimiento de un caballeroen el ajedrez . Para mayor r , el diferencial actúa como un movimiento de caballero generalizado.

Functor derivado [ editar ]

Artículo principal: Funtor derivado

Supongamos que se nos da una covariante dejó funtor exacto F  : A → B entre dos categorías abelianas A y B . Si 0 → A → B → C → 0 es una secuencia corta y exacta en A , la aplicación de F produce la secuencia exacta 0 → F ( A ) → F ( B ) → F ( C) y se podría preguntar cómo continuar esta secuencia hacia la derecha para formar una secuencia larga y exacta. Estrictamente hablando, esta pregunta está mal planteada, ya que siempre hay muchas formas diferentes de continuar una secuencia exacta dada a la derecha. Pero resulta que (si A es "agradable" suficiente) hay una canónica manera de hacerlo, dado por la derecha derivada de funtores F . Para cada i ≥ 1, hay un functor R ⁱ F : A → B , y la secuencia anterior continúa así: 0 → F ( A ) → F ( B ) → F ( C ) →R ¹ F ( A ) → R ¹ F ( B ) → R ¹ F ( C ) → R ² F ( A ) → R ² F ( B ) → .... De esto vemos que F es un functor exacto si y solo si R ¹ F = 0; así que, en cierto sentido, los funtores derivados de F miden "qué tan lejos" está F de ser exacto.

Functorialidad [ editar ]

Una aplicación continua de espacios topológicos da lugar a un homomorfismo entre su n º grupos de homologíapara todos n . Este hecho básico de la topología algebraica encuentra una explicación natural a través de ciertas propiedades de los complejos de cadenas. Como es muy común estudiar varios espacios topológicos simultáneamente, en el álgebra homológica se lleva a la consideración simultánea de complejos de cadenas múltiples.

Un morfismo entre dos complejos de cadenas,$${\ displaystyle F: C _ {\ bullet} \ a D _ {\ bullet},} Es una familia de homomorfismos de grupos abelianos. $${\ displaystyle F_ {n}: C_ {n} \ a D_ {n}} que conmutan con los diferenciales, en el sentido de que $${\ displaystyle F_ {n-1} \ circ d_ {n} ^ {C} = d_ {n} ^ {D} \ circ F_ {n}}para todos los n . Un morfismo de complejos de cadena induce un morfismo.$${\ displaystyle H _ {\ bullet} (F)} de sus grupos de homología, constituidos por los homomorfismos. $${\ displaystyle H_ {n} (F): H_ {n} (C) \ a H_ {n} (D)}para todos los n . Un morfismo Fse denomina cuasi isomorfismo si induce un isomorfismo en la n homología de todo n .

Muchas construcciones de complejos de la cadena que surgen en álgebra y geometría, incluyendo homología singular , tienen el siguiente functoriality propiedad: si dos objetos X e Y están conectados por un mapa f , entonces los complejos de la cadena asociados están conectados por un morfismo$${\ displaystyle F = C (f): C _ {\ bullet} (X) \ a C _ {\ bullet} (Y),} y además, la composición. $${\ displaystyle g \ circ f}de los mapas f :  X  →  Y y g :  Y  →  Z induce el morfismo$${\ displaystyle C (g \ circ f): C _ {\ bullet} (X) \ a C _ {\ bullet} (Z)} que coincide con la composicion $${\ displaystyle C (g) \ circ C (f).} De ello se deduce que los grupos de homología $${\ displaystyle H _ {\ bullet} (C)} También son funcionales, por lo que los morfismos entre objetos algebraicos o topológicos dan lugar a mapas compatibles entre su homología.

La siguiente definición surge de una situación típica en álgebra y topología. Un triple formado por complejos de tres cadenas.$${\ displaystyle L _ {\ bullet}, M _ {\ bullet}, N _ {\ bullet}} y dos morfismos entre ellos, $${\ displaystyle f: L _ {\ bullet} \ to M _ {\ bullet}, g: M _ {\ bullet} \ to N _ {\ bullet},}se llama un triple exacto, o una secuencia corta corta de complejos , y se escribe como

$${\ displaystyle 0 \ longrightarrow L _ {\ bullet} {\ overset {f} {\ longrightarrow}} M _ {\ bullet} {\ overset {g} {\ longrightarrow}} N _ {\ bullet} \ longrightarrow 0,}

si para cualquier n , la secuencia

$${\ displaystyle 0 \ longrightarrow L_ {n} {\ overset {f_ {n}} {\ longrightarrow}} M_ {n} {\ overset {g_ {n}} {\ longrightarrow}} N_ {n} \ longrightarrow 0}

Es una secuencia corta y exacta de grupos abelianos. Por definición, esto significa que f _n es una inyección , g _nes un surjection , y Im f _n  = Ker g _n . Uno de los teoremas más básicos del álgebra homológica, a veces conocido como el lema zig-zag , afirma que, en este caso, existe una secuencia larga y exacta en la homología.

$${\ displaystyle \ ldots \ longrightarrow H_ {n} (L) {\ overset {H_ {n} (f)} {\ longrightarrow}} H_ {n} (M) {\ overset {H_ {n} (g)} {\ longrightarrow}} H_ {n} (N) {\ overset {\ delta _ {n}} {\ longrightarrow}} H_ {n-1} (L) {\ overset {H_ {n-1} (f) } {\ longrightarrow}} H_ {n-1} (M) \ longrightarrow \ ldots,}

donde los grupos de homología de L , M y N se siguen cíclicamente, y δ _n son ciertos homomorfismos determinados por f y g , llamados homomorfismos de conexión . Las manifestaciones topológicas de este teorema incluyen la secuencia de Mayer-Vietoris y la secuencia exacta larga para la homología relativa .

Aspectos fundacionales [ editar ]

Las teorías de la cohomología se han definido para muchos objetos diferentes, como espacios topológicos , poleas , grupos , anillos , álgebras de Lie y algas C * . El estudio de la geometría algebraica moderna sería casi impensable sin la cohomología de la gavilla .

Central para el álgebra homológica es la noción de secuencia exacta ; Estos pueden ser utilizados para realizar cálculos reales. Una herramienta clásica del álgebra homológica es la del funtor derivado ; Los ejemplos más básicos son los funtores Ext y Tor .

Con un conjunto diverso de aplicaciones en mente, era natural tratar de poner todo el tema de manera uniforme. Hubo varios intentos antes de que se estableciera el tema. Una historia aproximada se puede enunciar de la siguiente manera:

• Cartan - Eilenberg : en su libro de 1956 "Álgebra homológica", estos autores usaron resoluciones de módulos proyectivos e inyectivos .
• 'Tohoku': el enfoque en un célebre artículo de Alexander Grothendieck que apareció en la Segunda Serie de la Revista Matemática Tohoku en 1957, utilizando el concepto de categoría abeliana (para incluir las gavillasde los grupos abelianos).
• La categoría derivada de Grothendieck y Verdier . Las categorías derivadas se remontan a la tesis de Verdier en 1967. Son ejemplos de categorías trianguladas utilizadas en varias teorías modernas.

Estos pasan de la computabilidad a la generalidad.

El martillo computacional por excelencia es la secuencia espectral ; estos son esenciales en los enfoques de Cartan-Eilenberg y Tohoku donde se necesitan, por ejemplo, para calcular los funtores derivados de una composición de dos funtores. Las secuencias espectrales son menos esenciales en el enfoque de la categoría derivada, pero todavía desempeñan un papel cada vez que se necesitan cálculos concretos.

Ha habido intentos de teorías "no conmutativas" que extienden la primera cohomología como torsores(importante en la cohomología de Galois ).