monoide (u objeto monoide ) ( M , μ, η) en una categoría monoidal ( C , ⊗, I ) es un objeto M junto con dos morfismos
- μ: M ⊗ M → M llamada multiplicación ,
- η: I → M unidad llamada ,
tal que el diagrama del pentágono
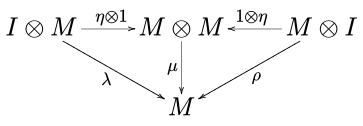
y el diagrama de unitor
conmutar. En las notaciones anteriores, I es el elemento unitario y α, λ y ρ son, respectivamente, la asociatividad, la identidad izquierda y la identidad derecha de la categoría C monoidal .
Supongamos que la categoría monoidal C tiene una simetría γ. Un monoide M en C es conmutativo cuando μ oγ = μ.
Ejemplos [ editar ]
- Un objeto monoide en Set , la categoría de conjuntos (con la estructura monoidal inducida por el producto cartesiano), es un monoide en el sentido habitual.
- Un objeto monoide en Top , la categoría de espacios topológicos (con la estructura monoidal inducida por la topología del producto ), es un monoide topológico .
- Un objeto monoide en la categoría de monoides (con el producto directo de monoides) es solo un monoide conmutativo . Esto se desprende fácilmente del teorema de Eckmann-Hilton .
- Un objeto monoid en la categoría de completa Join-semiretículo Sup (con la estructura monoidal inducido por el producto cartesiano) es un unital quantale .
- Un objeto monoide en ( Ab , ⊗ Z , Z ), la categoría de grupos abelianos , es un anillo .
- Para un anillo conmutativo R , un objeto monoide en
- ( R - Mod , ⊗ R , R ), la categoría de módulos sobre R , es una R - álgebra .
- La categoría de módulos graduados es un R-álgebra graduada .
- La categoría de complejos de cadenas es un dg-algebra .
- Un objeto monoid en K - Vect , la categoría de los espacios vectoriales (de nuevo, con el producto tensorial), es un K - álgebra , y un objeto comonoid es un K - coalgebra .
- Para cualquier categoría C , la categoría [ C , C ] de sus endofunctors tiene una estructura monoidal inducida por la composición y el funtor identidad I C . Un objeto monoid en [ C , C ] es una mónada en C .
- Para cualquier categoría con productos finitos , cada objeto se convierte en un objeto comonoide a través del morfismo diagonal. Dualmente, en una categoría con coproductos finitos, cada objeto se convierte en un objeto monoide a través de.
Categorías de monoides [ editar ]
Dados dos monoides ( M , μ, η) y ( M ', μ', η ') en una categoría monoidal C , un morfismo f : M → M ' es un morfismo de los monoides cuando
- f o μ = μ ' o ( f ⊗ f ),
- f o η = η '.
En otras palabras, los siguientes diagramas.
conmutar.
La categoría de monoides en C y sus morfismos monoides está escrito Lu C .
factorización de un monoide libre es una secuencia de subconjuntos de palabras con la propiedad de que cada palabra en el monoide libre puede escribirse como una concatenación de elementos extraídos de los subconjuntos. El teorema de Chen-Fox-Lyndon establece que las palabras de Lyndonproporcionan una factorización. El teorema de Schützenberger relaciona la definición en términos de una propiedad multiplicativa con una propiedad aditiva.
Deje A * sea el monoide libre en un alfabeto A . Sea X i una secuencia de subconjuntos de A * indexados por un conjunto de índices I totalmente ordenado . Una factorización de una palabra w en A * es una expresión
con y .
Teorema de Chen-Fox-Lyndon [ editar ]
Una palabra de Lyndon sobre un alfabeto totalmente ordenado A es una palabra que es lexicográficamentemenor que todas sus rotaciones. [1] El teorema de Chen-Fox-Lyndon establece que cada cadena puede formarse de una manera única al concatenar una secuencia no creciente de palabras de Lyndon. Por lo tanto, si X l es el conjunto único { l } de cada palabra de Lyndon l , con el conjunto de índices L de las palabras de Lyndon ordenadas lexicográficamente, obtenemos una factorización de A * . [2] Tal factorización se puede encontrar en el tiempo lineal. [3]
Bisección [ editar ]
Ejemplos:
- A = { a , b }, X 0 = { a * b }, X 1 = { a }.
Si X , Y son conjuntos separados de palabras no vacías, entonces ( X , Y ) es una bisección de A * si y solo si [5]
Como consecuencia, para cualquier partición P , Q de A + hay una bisección único ( X , Y ) con X un subconjunto de P y Y un subconjunto de Q . [6]
Schützenberger teorema [ editar ]
Este teorema establece que una secuencia X i de subconjuntos de A * forma una factorización si y solo si se cumplen dos de las siguientes tres afirmaciones:
- Cada elemento de A * tiene al menos una expresión en la forma requerida;
- Cada elemento de A * tiene como máximo una expresión en la forma requerida;
- Cada conjugado de clase C cumple solo con uno de los monoides M i = X i * y los elementos de C en M iestán conjugados en M i .
monoide sintáctica M ( L ) de un lenguaje formal L es la más pequeña monoid que reconoce el lenguaje L .
Cociente sintáctico [ editar ]
El monoide libre en un conjunto dado es el monoide cuyos elementos son todas las cadenas de cero o más elementos de ese conjunto, con la concatenación de cadenas como la operación monoides y la cadena vacíacomo el elemento de identidad . Dado un subconjunto de un monoide libre , uno puede definir conjuntos que consisten en inversos formales de izquierda o derecha de elementos en. Estos se llaman cocientes , y uno puede definir cocientes derecho o izquierdo, dependiendo de qué lado se está concatenando. Así, el cociente correcto de por un elemento desde es el conjunto
Del mismo modo, el cociente de la izquierda es
Equivalencia sintáctica [ editar ]
El cociente sintáctico induce una relación de equivalencia en M , llamada relación sintáctica , o equivalencia sintáctica (inducida por S ). La equivalencia sintáctica correcta es la relación de equivalencia.
Del mismo modo, la relación sintáctica izquierda es.
La definición se extiende a una congruencia definida por un subconjunto S de un monoid general M . Un conjunto disyuntivo es un subconjunto S tal que la congruencia sintáctica definida por S es la relación de igualdad. [3]
Llamemos la clase de equivalencia de Por la congruencia sintáctica. La congruencia sintáctica es compatible con la concatenación en el monoide, ya que uno tiene
para todos . Por lo tanto, el cociente sintáctico es un morfismo monoide , e induce un monoide cociente
Este monoide se llama la monoid sintáctica de S . Se puede demostrar que es el monoide más pequeño el que reconoce S ; es decir, M ( S ) reconoce S , y por cada monoid N reconociendo S , M ( S ) es un cociente de un submonoide de N . El monoid sintáctica de S es también la monoid transición del autómata mínimo de S . [1] [2] [4]
De manera similar, un idioma L es regular si y solo si la familia de cocientes
es finito [1] La prueba que muestra la equivalencia es bastante fácil. Suponga que una cadena x es leída por un autómata finito determinista , con la máquina avanzando al estado p . Si y es otra cadena leída por la máquina, que también termina en el mismo estado p , entonces claramente uno tiene. Así, el número de elementos en a lo sumo es igual al número de estados del autómata y es a lo sumo el número de estados finales. Supongamos, a la inversa, que el número de elementos enes finito Entonces se puede construir un autómata donde es el conjunto de estados, es el conjunto de estados finales, el lenguaje L es el estado inicial y la función de transición viene dada por. Claramente, este autómata reconoce L . Así, un idioma L es reconocible si y solo si el conjuntoes finito Tenga en cuenta que esta prueba también construye el autómata mínimo.
Ejemplos [ editar ]
- Sea L el lenguaje sobre A = { a , b } de palabras de longitud uniforme. La congruencia sintáctica tiene dos clases, L en sí y L 1 , las palabras de longitud impar. El monoide sintáctico es el grupo de orden 2 en { L , L 1}. [6]
- El monoide bicíclico es el monoide sintáctico del lenguaje Dyck (el lenguaje de conjuntos equilibrados de paréntesis).
- El monoide libre en A (| A |> 1) es el monoide sintáctico del lenguaje { ww R | w en A *}, donde w R denota la inversión de la palabra w .
- Cada monoide finito es homomorfo [ clarificación necesaria ] al monoid sintáctico de algún lenguaje no trivial, [7]pero no todo monoid finito es isomorfo a un monoide sintáctico. [8]
- Cada grupo finito es isomorfo al monoide sintáctico de algún lenguaje no trivial. [7]
- El lenguaje sobre { a , b } en el que el número de apariciones de a y b son congruentes módulo 2 n es un lenguaje grupal con monoide sintáctico Z / 2 n . [5]
- Los monoides traza son ejemplos de monoides sintácticos.
- Marcel-Paul Schützenberger [9] caracterizó a los idiomas sin estrellas como aquellos con monoides sintácticos aperiódicos finitos .
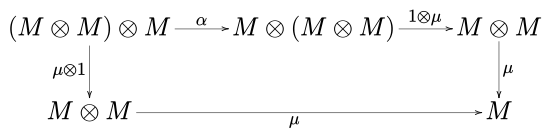


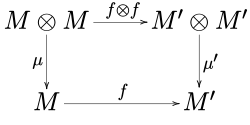













![{\ displaystyle [s] _ {S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9840432df082a10384e711f63df10ae22d25bdf9)

![{\ displaystyle [s] _ {S} [t] _ {S} = [st] _ {S}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de1a348e052caf217cb4a04abf6a9aa95d07aa3)









No hay comentarios:
Publicar un comentario