MATEMÁTICAS - LISTA DE TEMAS DE ÁLGEBRA ABSTRACTA

límite inverso (también llamado límite o límite proyectivo ) es una construcción que permite "pegar" varios objetos relacionados , especificando la manera precisa del proceso de pegado mediante morfismos entre los objetos. Los límites inversos se pueden definir en cualquier categoría .

Definición formal [ editar ]

Objetos algebraicos [ editar ]

Comenzamos con la definición de un sistema inverso (o sistema proyectivo) de grupos y homomorfismos . Sea ( I , ≤) un poset dirigido (no todos los autores requieren que yo sea ​​dirigido). Sea ( A _i ) _i ∈ I ser una familia de grupos y supongamos que tenemos una familia de homomorfismos f _ij : Un _j → A _i para todos i ≤ j (nota de la orden), llamados mapas de unión, con las siguientes propiedades:

1. f _ii es la identidad en A _i ,
2. f _ik = f _ij o f _jk para todos i ≤ j ≤ k .

Luego, el par (( A _i ) _i ∈ I , ( f _ij ) _{i ≤ j ∈ I} ) se denomina sistema inverso de grupos y morfismos sobre I , y los morfismos f _ij se denominan morfismos de transición del sistema.

Definimos el límite inverso del sistema inverso (( A _i ) _i ∈ I , ( f _ij ) _{i ≤ j ∈ I} ) como un subgrupo particular del producto directo de las A _i :

$${\ displaystyle A = \ varprojlim _ {i \ in I} {A_ {i}} = \ left \ {\ left. {\ vec {a}} \ in \ prod _ {i \ in I} A_ {i} \; \ right | \; a_ {i} = f_ {ij} (a_ {j}) {\ text {para todos}} i \ leq j {\ text {in}} I \ right \}.}

El límite inverso A viene equipado con proyecciones naturales π _i : A → A _i que escoger el i ésimo componente del producto directo para cada i en I . El límite inverso y las proyecciones naturales satisfacen una propiedad universal descrita en la siguiente sección.

Esta misma construcción puede llevarse a cabo si los A _i son conjuntos , ^[1] semigrupos, ^[1] espacios topológicos, ^[1] anillos , módulos (sobre un anillo fijo), álgebras (sobre un anillo fijo), etc. , y los homomorfismos son morfismos en la categoría correspondiente . El límite inverso también pertenecerá a esa categoría.

Definición general [ editar ]

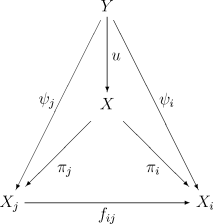
El límite inverso se puede definir de manera abstracta en una categoría arbitraria por medio de una propiedad universal . Sea ( X _i , f _ij ) un sistema inverso de objetos y morfismos en una categoría C (la misma definición que arriba). El límite inverso de este sistema es un objeto X en C junto con los morfismos π _i : X → X _i (llamados proyecciones ) que satisfacen π _i = f _ij o π _j para todas las i≤ j . El par ( X , π _i ) debe ser universal en el sentido de que para cualquier otro par ( Y , ψ _i ) (es decir, ψ _i : Y → X _i con ψ _i = f _ij o ψ _j para todos i ≤ j ) existe un morfismo único u : Y → X tal que el diagrama

conmuta por todo i ≤ j , por lo que basta con demostrar que ψ _i = π _i o u para todo i . El límite inverso se denota a menudo

$${\ displaystyle X = \ varprojlim X_ {i}}

con el sistema inverso ( X _i , f _ij ) siendo entendido.

En algunas categorías, el límite inverso no existe. Sin embargo, si lo hace, es único en un fuerte sentido: dado cualquier otro límite inverso X ′ existe un isomorfismo único X ′ → X que conmuta con los mapas de proyección.

Notamos que un sistema inverso en una categoría C admite una descripción alternativa en términos de funtores . Cualquier conjunto parcialmente ordenado I puede ser considerado como una pequeña categoría donde los morfismos consisten en flechas i → j si y solo si i ≤ j . Un sistema inverso es entonces solo un functor contravariante I → C , y el functor de límite inverso $${\ displaystyle \ varprojlim: C ^ {I ^ {op}} \ rightarrow C}Es un functor covariante .

Ejemplos [ editar ]

• El anillo de enteros p -ádicos es el límite inverso de los anillos Z / p ⁿ Z (ver aritmética modular ) con el índice establecido como los números naturales con el orden habitual, y los morfismos son "tomar el resto". Es decir, se consideran secuencias de enteros.$${\ displaystyle (n_ {0}, n_ {1}, \ cdots)} de tal manera que cada elemento de la secuencia "proyecta" hasta los anteriores, a saber, que $${\ displaystyle n_ {i} \ equiv n_ {j} {\ mbox {mod}} p ^ {i + 1} cuando {\ displaystyle i La topología natural en los enteros p -adic es la implícita aquí, a saber, la topología del producto con conjuntos de cilindros como los conjuntos abiertos.
• El anillo $${\ displaystyle \ textstyle R [[t]]}Las series de poder formales sobre un anillo conmutativo R pueden considerarse como el límite inverso de los anillos.$${\ displaystyle \ textstyle R [t] / t ^ {n} R [t]}, indexados por los números naturales como se ordena generalmente, con los morfismos de $${\ displaystyle \ textstyle R [t] / t ^ {n + j} R [t]} a $${\ displaystyle \ textstyle R [t] / t ^ {n} R [t]} Dada por la proyección natural.
• Los grupos pro-finitos se definen como límites inversos de grupos finitos (discretos).
• Deje que el conjunto de índices I de un sistema inverso ( X _i , f _ij ) tenga el elemento m mayor . Entonces, la proyección natural π _m : X → X _m es un isomorfismo.
• Los límites inversos en la categoría de espacios topológicos se dan colocando la topología inicial en el límite inverso de la teoría subyacente subyacente. Esto se conoce como la topología límite .
  • El conjunto de cadenas infinitas es el límite inverso del conjunto de cadenas finitas y, por lo tanto, está dotado de la topología límite. Como los espacios originales son discretos , el espacio límite está totalmente desconectado . Esta es una forma de realizar los números p -adic y el conjunto de Cantor(como cadenas infinitas).
• Sea ( I , =) el orden trivial (no dirigido). El límite inverso de cualquier sistema inverso correspondiente es solo el producto .
• Considero que consto de tres elementos i , j y k con i ≤ j e i ≤ k (no dirigido). El límite inverso de cualquier sistema inverso correspondiente es el retroceso .

Funtores derivados del límite inverso [ editar ]

Para una categoría abeliana C , el functor de límite inverso

$${\ displaystyle \ varprojlim: C ^ {I} \ rightarrow C}

se deja exacto . Si I es ordenado (no simplemente ordenado parcialmente) y contable , y C es la categoría Ab de los grupos abelianos, la condición Mittag-Leffler es una condición en los morfismos de transición f _ij que garantiza la exactitud de$${\ displaystyle \ varprojlim}. Específicamente, Eilenberg construyó un funtor.

$${\ displaystyle \ varprojlim {} ^ {1}: \ operatorname {Ab} ^ {I} \ rightarrow \ operatorname {Ab}}

(pronunciado "lim one") de modo que si ( A _i , f _ij ), ( B _i , g _ij ) y ( C _i , h _ij ) son tres sistemas proyectivos de grupos abelianos, y

$${\ displaystyle 0 \ rightarrow A_ {i} \ rightarrow B_ {i} \ rightarrow C_ {i} \ rightarrow 0}

Es una secuencia exacta corta de sistemas inversos, entonces

$${\ displaystyle 0 \ rightarrow \ varprojlim A_ {i} \ rightarrow \ varprojlim B_ {i} \ rightarrow \ varprojlim C_ {i} \ rightarrow \ varprojlim {} ^ {1} A_ {i}}

Es una secuencia exacta en Ab .

Condición de Mittag-Leffler [ editar ]

Si los rangos de los morfismos de un sistema inverso de grupos abelianos ( A _i , f _ij ) son estacionarios , es decir, para cada k existe j ≥ k tal que para todo i ≥ j  :$${\ displaystyle f_ {kj} (A_ {j}) = f_ {ki} (A_ {i})}uno dice que el sistema satisface la condición Mittag-Leffler .

Bourbaki dio el nombre "Mittag-Leffler" para esta condición en su capítulo sobre estructuras uniformes para obtener un resultado similar sobre los límites inversos de los espacios uniformes completos de Hausdorff. Mittag-Leffler utilizó un argumento similar en la prueba del teorema de Mittag-Leffler .

Las siguientes situaciones son ejemplos en los que se cumple la condición Mittag-Leffler:

• Un sistema en el que los morfismos f _ij son sobreyectivos.
• Un sistema de espacios vectoriales de dimensión finita o grupos abelianos finitos o módulos de longitud finita o módulos Artinianos.

Un ejemplo donde $${\ displaystyle \ varprojlim {} ^ {1}}no es cero se obtiene tomando I a ser la no negativos números enteros , dejando que A _i= p ⁱ Z , B _i = Z , y C _i = B _i / A _i = Z / p ⁱ Z . Entonces

$${\ displaystyle \ varprojlim {} ^ {1} A_ {i} = \ mathbf {Z} _ {p} / \ mathbf {Z}}

donde Z _p denota los enteros p-adic .

Otros resultados [ editar ]

De manera más general, si C es una categoría abeliana arbitraria que tiene suficientes inyecciones , también lo tiene C ^I , y los funtores derivados correctos del funtor de límite inverso se pueden definir. El n º derecho funtor derivado se denota

$${\ displaystyle R ^ {n} \ varprojlim: C ^ {I} \ rightarrow C.}

En el caso en que C satisface el axioma de Grothendieck (AB4 *) , Jan-Erik Roos generalizó el functor lim ¹ en Ab ^I a una serie de functors lim ⁿ tal que

$${\ displaystyle \ varprojlim {} ^ {n} \ cong R ^ {n} \ varprojlim.}

Se pensó durante casi 40 años que Roos había demostrado (en Sur les foncteurs dérivés de lim. Aplicaciones. ) Que lim ¹ A _i = 0 para ( A _i , f _ij ) un sistema inversa con morfismos de transición suprayectivos y I el conjunto de enteros no negativos (tales sistemas inversos a menudo se denominan " secuencias Mittag-Leffler "). Sin embargo, en 2002, Amnon Neeman y Pierre Deligne construyeron un ejemplo de dicho sistema en una categoría satisfactoria (AB4) (además de (AB4 *)) con lim ¹ A _i≠ 0. Roos ha demostrado ya que (en "funtores derivados de límite inverso revisited") que su resultado es correcto si C tiene un conjunto de generadores (además de satisfacer (AB3) y (AB4 *)).

Barry Mitchell ha demostrado (en "La dimensión cohomológico de un conjunto dirigido") que si I tiene cardinalidad$${\ displaystyle \ aleph _ {d}}(el d th cardinal infinito ), entonces R ⁿ lim es cero para todos n ≥ d + 2. Esto se aplica a los diagramas I-indexados en la categoría de los módulos R , con R a anillo conmutativo; no es necesariamente cierto en una categoría abeliana arbitraria (ver "Functores derivados de límites inversos de Roos revisados" para ver ejemplos de categorías abelianas en las que lim ⁿ , en diagramas indexados por un conjunto contable, es distinto de cero para  n  > 1).

Conceptos relacionados y generalizaciones [ editar ]

El doble categórico de un límite inverso es un límite directo (o límite inductivo). Los conceptos más generales son los límites y colimits de la teoría de categorías. La terminología es algo confusa: los límites inversos son límites, mientras que los límites directos son colimits.

Un grupo cociente o grupo factorial es un grupo matemático que seobtiene al agregar elementos similares de un grupo más grande utilizando una relación de equivalencia que preserva la estructura del grupo. Por ejemplo, el grupo cíclico de módulo de adición n puede obtenerse de los enteros identificando elementos que difieren en un múltiplo de n y definiendo una estructura de grupo que opera en cada clase (conocida como clase de congruencia ) como una sola entidad. Es parte del campo matemático conocido como teoría de grupos .

En un cociente de un grupo, la clase de equivalencia del elemento de identidad es siempre un subgrupo normal del grupo original, y las otras clases de equivalencia son precisamente los cosets de ese subgrupo normal. El cociente resultante se escribe G / N , donde G es el grupo original y N es el subgrupo normal. (Esto se pronuncia " G mod N ", donde "mod" es la abreviatura de módulo ).

Gran parte de la importancia de los grupos cocientes se deriva de su relación con los homomorfismos . El primer teorema de isomorfismoestablece que la imagen de cualquier grupo G bajo un homomorfismo es siempre isomorfo a un cociente de G . Específicamente, la imagen de G bajo un homomorfismo φ : G → H es isomorfa a G / ker ( φ )donde ker ( φ ) denota el núcleo de φ .

La noción dual de un grupo cociente es un subgrupo , que son las dos formas principales de formar un grupo más pequeño a partir de uno más grande. Cualquier subgrupo normal tiene un grupo de cociente correspondiente, formado a partir del grupo más grande al eliminar la distinción entre los elementos del subgrupo. En la teoría de categorías , los grupos de cocientes son ejemplos de objetos de cociente , que son duales a los subobjetos . Para otros ejemplos de objetos de cociente, vea el anillo de cociente , el espacio de cociente (álgebra lineal) , el espacio de cociente (topología) y el conjunto de cociente .

Definición e ilustración [ editar ]

Dado un grupo G y un subgrupo H , y un elemento a en G , se puede considerar el coset izquierdo correspondiente : aH  : = { ah  : h en H }. Los cosets son una clase natural de subconjuntos de un grupo; por ejemplo, considere el grupo abeliano G de enteros , con la operación definida por la suma habitual, y el subgrupo H de enteros pares. Luego hay exactamente dos cosets: 0 + H , que son los enteros pares, y 1 + H, que son los enteros impares (aquí estamos usando la notación aditiva para la operación binaria en lugar de la notación multiplicativa).

Para un subgrupo general H , es deseable definir una operación de grupo compatible en el conjunto de todos los posibles cosets, { aH  : a en G }. Esto es posible exactamente cuando H es un subgrupo normal , como veremos a continuación. Un subgrupo N de un grupo G es normal si y sólo si la igualdad clase lateral aN = Na mantiene para todos una en G . Un subgrupo normal de G se denota N ◁ G .

Definición [ editar ]

Deje que N sea un subgrupo normal de un grupo G . Definimos el conjunto G / N como el conjunto de todos los cosets izquierdos de N en G , es decir, G / N = { aN  : a ∈ G } . Defina una operación en G / N como sigue. Para cada aN y bN en G / N , el producto de aN y bN es ( aN ) ( bN). Esto define una operación en G / N si imponemos ( aN ) ( bN ) = ( ab ) N , porque ( ab ) N no depende de la elección de los representantes a y b : si xN = aN e yN = bN para algunos x , y en G , entonces

(ab) N = un (BN) = a (yN) = a (NY) = (a) Y = (Xn) Y = x (NY) = x (yn) = (xy) N .

Aquí hemos utilizado de manera importante que N es un subgrupo normal. Uno cheques que esta operación en G / N es asociativa, tiene elemento de identidad N , y la inversa de un elemento aN de G / N es un ^-1 N . Por lo tanto, el conjunto G / N junto con la operación definida anteriormente forma un grupo; esto se conoce como el grupo cociente de G por N .

Debido a la normalidad de N , las clases laterales izquierda y clases laterales derechas de N en G son iguales, y así que podría tener lugar definido G / N para ser el conjunto de clases laterales derechas de N en G .

Ejemplo: Módulo de adición 6 [ editar ]

Por ejemplo, considere el grupo con módulo de adición 6: G = {0, 1, 2, 3, 4, 5}. Considere el subgrupo N = {0, 3}, que es normal porque G es abeliano . Entonces el conjunto de cosets (izquierda) es de tamaño tres:

G / N = { a + N  : a ∈ G } = {{0, 3}, {1, 4}, {2, 5}} = {0+ N , 1+ N , 2+ N }.

La operación binaria definida anteriormente convierte este conjunto en un grupo, conocido como grupo cociente, que en este caso es isomorfo al grupo cíclico de orden 3.

Motivación para el nombre "cociente" [ editar ]

La razón por la que G / N se denomina grupo de cociente proviene de la división de enteros . Cuando se divide 12 por 3, se obtiene la respuesta 4 porque se pueden agrupar 12 objetos en 4 subcolecciones de 3 objetos. El grupo cociente es la misma idea, aunque terminamos con un grupo para una respuesta final en lugar de un número porque los grupos tienen más estructura que una colección arbitraria de objetos.

Para elaborar, al mirar G / N con N un subgrupo normal de G , la estructura de grupo se usa para formar un "reagrupamiento" natural. Estas son las clases laterales de N en G . Debido a que comenzamos con un grupo y un subgrupo normal, el cociente final contiene más información que solo el número de cosets (que es lo que produce la división regular), pero en su lugar tiene una estructura de grupo.

Ejemplos [ editar ]

Enteros pares e impares [ editar ]

Considere el grupo de enteros Z (bajo adición) y el subgrupo 2 Z que consiste en todos los enteros pares. Este es un subgrupo normal, porque Z es abeliano . Solo hay dos cosets: el conjunto de enteros pares y el conjunto de enteros impares; por lo tanto, el grupo cociente Z / 2 Z es el grupo cíclico con dos elementos. Este grupo cociente es isomórfico con el conjunto {0, 1} con módulo de adición 2; informalmente, a veces se dice que Z / 2 Z es igualal conjunto {0, 1} con módulo de adición 2.

Ejemplo explicado con más detalle ...

Dejar $${\ displaystyle \ gamma (m) =} restos de $${\ displaystyle m \ in \ mathbb {Z}} cuando dividiendo por $${\ displaystyle 2}. 
Entonces$${\ displaystyle \ gamma (m) = 0} cuando $${\ displaystyle m} es parejo y $${\ displaystyle \ gamma (m) = 1} cuando $${\ displaystyle m}es impar. 
Por definición de$${\ displaystyle \ gamma}, el núcleo de $${\ displaystyle \ gamma}, 
Ker ($${\ displaystyle \ gamma}) $${\ displaystyle = \ {m \ in \ mathbb {Z}: \ gamma (m) = 0 \}}, es el conjunto de todos los enteros pares. 
Dejar$${\ displaystyle H =} ker$${\ displaystyle \ gamma}). 
Entonces$${\ displaystyle H} es un subgrupo, porque la identidad en $${\ displaystyle \ mathbb {Z}}, cual es $${\ displaystyle 0}, es en $${\ displaystyle H}, 
la suma de dos enteros pares es par y por lo tanto si$${\ displaystyle m} y $${\ displaystyle n} están en $${\ displaystyle H}, $${\ displaystyle m + n} es en $${\ displaystyle H}(cierre) 
y si$${\ displaystyle m} incluso, $${\ displaystyle -m} también es par y muy $${\ displaystyle H}Contiene sus inversos. 
Definir$${\ displaystyle \ mu:} $${\ displaystyle \ mathbb {Z}} / H$${\ displaystyle \ to \ mathbb {Z} _ {2}} como $${\ displaystyle \ mu (aH) = \ gamma (a)} para $${\ displaystyle a \ in \ mathbb {Z}}
y $${\ displaystyle \ mathbb {Z}}/ H es el grupo cociente de cosets izquierdos; $${\ displaystyle \ mathbb {Z}} / H$${\ displaystyle = \ {H, 1 + H \}}. 
Por cierto hemos definido$${\ displaystyle \ mu}, $${\ displaystyle \ mu (aH)} es $${\ displaystyle 1} Si $${\ displaystyle a} es extraño y $${\ displaystyle 0} Si $${\ displaystyle a}incluso. 
Así,$${\ displaystyle \ mu} es un isomorfismo de $${\ displaystyle \ mathbb {Z}}/ H a$${\ displaystyle \ mathbb {Z} _ {2}}.

Restos de la división de enteros [ editar ]

Una ligera generalización del último ejemplo. Una vez más, considere el grupo de enteros Z en adición. Sea n un entero positivo. Consideraremos el subgrupo n Z de Z que consiste en todos los múltiplos de n . Una vez más, n Z es normal en Z porque Z es abeliano. Los cosets son la colección { n Z , 1+ n Z , ..., ( n −2) + n Z , ( n −1) + n Z}. Un entero k pertenece al coset r+ n Z , donde r es el resto al dividir k por n . El cociente Z / n Z puede considerarse como el grupo de "restos" módulo n . Este es un grupo cíclico de orden n .

Raíces enteras complejas de 1 [ editar ]

Las clases laterales de las cuartas raíces de la unidad N en las raíces duodécimo de la unidad G .

Las duodécimas raíces de la unidad , que son puntos en el círculo complejo de unidades , forman un grupo abeliano multiplicativo G , que se muestra en la imagen de la derecha como bolas de colores con el número en cada punto que da su argumento complejo. Considere su subgrupo N hecho de las cuartas raíces de la unidad, mostradas como bolas rojas. Este subgrupo normal divide el grupo en tres cosets, que se muestran en rojo, verde y azul. Uno puede verificar que los cosets forman un grupo de tres elementos (el producto de un elemento rojo con un elemento azul es azul, la inversa de un elemento azul es verde, etc.). Así, el grupo cociente G / N es el grupo de tres colores, que resulta ser el grupo cíclico con tres elementos.

Sumas de enteros y números reales [ editar ]

Considere el grupo de números reales R debajo de la suma y el subgrupo Z de enteros. Los cosets de Z en R son todos conjuntos de la forma a + Z , con 0 ≤ a <1 font=""> un número real. La adición de dichos cosets se realiza sumando los números reales correspondientes y restando 1 si el resultado es mayor o igual que 1. El grupo cociente R / Z es isomorfo al grupo de círculos S ¹ , el grupo de números complejos de valor absoluto 1 bajo multiplicación, o correspondientemente, el grupo deRotaciones en 2D sobre el origen, es decir, el grupo ortogonal especial SO (2). Un isomorfismo es dado por f ( a + Z ) = exp (2 πia ) (vea la identidad de Euler ).

Matrices de números reales [ editar ]

Si G es el grupo de matrices reales invertibles 3 × 3 , y N es el subgrupo de matrices reales 3 × 3 con determinante 1, entonces N es normal en G (ya que es el núcleo del homomorfismo determinante ). Los cosets de N son los conjuntos de matrices con un determinante dado, y por lo tanto, G / N es isomorfo al grupo multiplicativo de números reales distintos de cero. El grupo N se conoce como el grupo lineal especial SL (3).

Aritmética modular entera [ editar ]

Considere el grupo abeliano Z ₄ = Z / 4 Z (es decir, el conjunto {0, 1, 2, 3} con módulo de adición 4) y su subgrupo {0, 2} . El grupo cociente Z ₄ / {0, 2} es {{0, 2}, {1, 3}} . Este es un grupo con elementos de identidad {0, 2} y operaciones de grupo como {0, 2} + {1, 3} = {1, 3} . Tanto el subgrupo {0, 2} como el grupo de cocientes {{0, 2}, {1, 3}} son isomorfos con Z ₂ .

La multiplicación de enteros [ editar ]

Considera el grupo multiplicativo. $${\ displaystyle G = \ mathbf {Z} _ {n ^ {2}} ^ {*}}. El conjunto N de n residuos n es un subgrupo multiplicativo isomorfo a$${\ displaystyle \ mathbf {Z} _ {n} ^ {*}}. Entonces, N es normal en G y el grupo de factores G / N tiene los cosets N , (1+ n ) N , (1+ n ) ² N, ..., (1+ n) ^n −1 N. El sistema de cifrado Paillier se basa en la conjetura de que es difícil determinar el coset de un elemento aleatorio de G sin conocer la factorización de n .

Propiedades [ editar ]

El grupo cociente G / G es isomorfo al grupo trivial (el grupo con un elemento), y G / { e } es isomorfo a G .

El orden de G / N , por definición el número de elementos, es igual a | G  : N | , El índice de N en G . Si G es finito, el índice también es igual a la orden de G dividido por el orden de N . Tenga en cuenta que G / N puede ser finito, aunque tanto G como N son infinitos (por ejemplo, Z / 2 Z ).

Existe un homomorfismo π  : G → G / N de un grupo suryectivo "natural" , que envía cada elemento g de G al coset de N al que pertenece g , es decir: π ( g ) = gN . El mapeo π a veces se llama la proyección canónica de G a G / N . Su núcleo es N .

Hay una correspondencia biyectiva entre los subgrupos de G que contienen N y los subgrupos de G / N ; si H es un subgrupo de G que contiene N , entonces el subgrupo correspondiente de G / N es π ( H ). Esta correspondencia se mantiene también para subgrupos normales de G y G / N , y se formaliza en el teorema de celosía .

Varias propiedades importantes de los grupos de cocientes se registran en el teorema fundamental sobre homomorfismos y los teoremas de isomorfismo .

Si G es abeliano , nilpotent , resoluble , cíclico o de tipo finito , entonces también lo es G / N .

Si H es un subgrupo en un grupo finito G , y el orden de H es la mitad del orden de G , entonces se garantiza que H es un subgrupo normal, por lo que G / H existe y es isomorfo a C ₂ . Este resultado también se puede declarar como "cualquier subgrupo del índice 2 es normal", y en esta forma se aplica también a grupos infinitos. Además, si p es el número primo más pequeño que divide el orden de un grupo finito, G , entonces si G / H tiene el orden p , H debe ser un subgrupo normal de G. ^[1]

Dada G y un subgrupo normal N , entonces G es una extensión de grupo de G / N por N . Uno podría preguntarse si esta extensión es trivial o dividida; en otras palabras, se podría preguntar si G es un producto directo o producto semidirecto de N y G / N . Este es un caso especial del problema de extensión . Un ejemplo en el que la extensión no está dividida es la siguiente: Sea G = Z ₄ = {0, 1, 2, 3} y N= {0, 2}, que es isomorfo a Z ₂ . Entonces G / N es también isomorfo a Z ₂ . Pero Z ₂ tiene solo el automorfismo trivial , por lo que el único producto semidirecto de N y G / N es el producto directo. Desde Z ₄ es diferente de Z ₂ × Z ₂ , se concluye que Gno es un producto semi-directa de N y G / N .

Cocientes de grupos de Lie [ editar ]

Si G es un grupo de Lie y N es un subgrupo de Lie normal de G , el cociente G / N también es un grupo de Lie. En este caso, el grupo original G tiene la estructura de un haz de fibras (específicamente, un director N -bundle ), con espacio base G / N y la fibra N .

Para un subgrupo N de Lie no normal , el espacio G / N de los cosets izquierdos no es un grupo, sino simplemente una variedad diferenciable sobre la que G actúa. El resultado es conocido como un espacio homogéneo .