MATEMÁTICAS - LISTA DE TEMAS DE ÁLGEBRA ABSTRACTA

operación binaria en un conjunto es un cálculo que combina dos elementos del conjunto (llamados operandos ) para producir otro elemento del conjunto. Más formalmente, una operación binaria es una operación de aridad de dos cuyos dos dominios y un codominio son el mismo conjunto. Los ejemplos incluyen las operaciones aritméticas elementales familiares de suma , resta , multiplicación y división . Otros ejemplos se encuentran fácilmente en diferentes áreas de las matemáticas, como la adición de vectores, matriz de multiplicación y conjugación en grupos .

Más precisamente, una operación binaria en un conjunto S es un mapa que envía elementos del producto cartesiano S × S a S : ^{[1] [2] [3]}

$${\ displaystyle \, f \ colon S \ times S \ rightarrow S.}

Debido a que el resultado de realizar la operación en un par de elementos de S es nuevamente un elemento de S, la operación se denomina operación binaria cerrada en S (o se expresa a veces como que tiene la propiedad de cierre ). ^[4] Si f no es una función , sino que es una función parcial , se denomina operación binaria parcial . Por ejemplo, la división de números reales es una operación binaria parcial, porque no se puede dividir por cero : un / 0 no está definido para cualquier real de una. Tenga en cuenta sin embargo, que tanto en el álgebra y la teoría de modelos las operaciones binarias consideradas se definen sobre todo de S × S .

A veces, especialmente en informática , el término se usa para cualquier función binaria .

Las operaciones binarias son la piedra angular de las estructuras algebraicas estudiadas en álgebra abstracta : son esenciales en las definiciones de grupos , monoides , semigrupos , anillos y más. En general, un magma es un conjunto junto con alguna operación binaria definida en él.

Propiedades y ejemplos [ editar ]

Ejemplos típicos de operaciones binarias son la suma (+) y la multiplicación (×) de números y matrices , así como la composición de funciones en un solo conjunto. Por ejemplo,

• En el conjunto de números reales R , f ( a , b ) = a + b es una operación binaria, ya que la suma de dos números reales es un número real.
• En el conjunto de números naturales N , f ( a , b ) = a + b es una operación binaria, ya que la suma de dos números naturales es un número natural. Esta es una operación binaria diferente a la anterior ya que los conjuntos son diferentes.
• En el conjunto M (2,2) de matrices 2 × 2 con entradas reales, f ( A , B ) = A + B es una operación binaria, ya que la suma de dos de estas matrices es otra matriz de 2 × 2 .
• En el conjunto M (2,2) de matrices 2 × 2 con entradas reales, f ( A , B ) = AB es una operación binaria, ya que el producto de dos de estas matrices es otra matriz de 2 × 2 .
• Para un conjunto dado C , vamos S ser el conjunto de todas las funciones h  : C → C . Defina f  : S × S → Spor f ( h ₁ , h ₂ ) ( c ) = h ₁ ∘ h ₂ ( c ) = h ₁ ( h ₂ ( c )) para toda c ∈ C , la composición de los dos funciones h ₁y h ₂ en S . Entonces f es una operación binaria, ya que la composición de las dos funciones es otra función en el conjunto C (es decir, un miembro de S ).

Muchas operaciones binarias de interés tanto en álgebra como en lógica formal son conmutativas , satisfaciendo f ( a , b ) = f ( b , a ) para todos los elementos a y b en S , o asociativa , satisfaciendo f ( f ( a , b ), c ) = f ( a , f ( b , c )) para todos a , b yc en s . Muchos también tienen elementos de identidad y elementos inversos .

Los primeros tres ejemplos anteriores son conmutativos y todos los ejemplos anteriores son asociativos.

En el conjunto de números reales R , la resta , es decir, f ( a , b ) = a - b , es una operación binaria que no es conmutativa ya que, en general, a - b ≠ b - a . Tampoco es asociativo, ya que, en general, a - ( b - c ) ≠ ( a - b ) - c; por ejemplo, 1 - (2 - 3) = 2 pero (1 - 2) - 3 = −4 .

En el conjunto de números naturales N , la operación binaria exponentiation , f ( a , b ) = a ^b , no es conmutativa ya que, en general , a ^b ≠ b ^a y tampoco es asociativa, ya que f ( f ( a , b ) , c ) ≠ f ( a , f ( b , c )) . Por ejemplo, con a = 2 , b = 3y c = 2 , f (2 ³ , 2) = f (8,2) = 8 ² = 64 , pero f (2,3 ² ) = f (2,9) = 2 ⁹ = 512 . Al cambiar el conjunto N al conjunto de enteros Z , esta operación binaria se convierte en una operación binaria parcial, ya que ahora está indefinida cuando a = 0 y b es un entero negativo. Para cualquiera de los conjuntos, esta operación tiene una identidad correcta (que es 1) ya que f ( a , 1) = a para todos aen el conjunto, que no es una identidad ( identidad de dos caras) ya que f (1, b ) ≠ b en general.

La división (/), una operación binaria parcial en el conjunto de números reales o racionales, no es conmutativa ni asociativa. La tetración (↑↑), como una operación binaria en los números naturales, no es conmutativa ni asociativa y no tiene ningún elemento de identidad.

Notación [ editar ]

Las operaciones binarias se escriben a menudo usando notación infija tal como un * b , un + b , un · b o (por yuxtaposición sin símbolo) ab más bien que por la notación funcional de la forma f ( un , b ) . Los poderes generalmente también se escriben sin operador, pero con el segundo argumento como superíndice .

Las operaciones binarias a veces usan el prefijo o (probablemente más a menudo) la notación de postfijo, que prescinde de paréntesis. También se denominan, respectivamente, notación polaca y notación polaca inversa .

Pareja y tupla [ editar ]

Una operación binaria, ab , depende del par ordenado ( a, b ) y así ( ab ) c (donde los paréntesis aquí significan que primero operan en el par ordenado ( a , b ) y luego operan en el resultado de eso usando el par (( ab ), c )) depende en general del par ordenado (( a , b ), c ). Por lo tanto, para el caso general, no asociativo, las operaciones binarias se pueden representar con árboles binarios .

Sin embargo:

• Si la operación es asociativa, ( ab ) c = a ( bc ), entonces el valor de ( ab ) c depende solo de la tupla ( a , b , c).
• Si la operación es conmutativa, ab = ba , entonces el valor de ( ab ) c depende solo de {{ a , b }, c }, donde las llaves indican conjuntos múltiples .
• Si la operación es tanto asociativa como conmutativa, entonces el valor de ( ab ) c depende solo del conjunto múltiple { a , b , c }.
• Si la operación es asociativa, conmutativa e idempotente , aa = a , entonces el valor de ( ab ) c depende solo del conjunto { a , b , c }.

Las operaciones binarias como ternarias las relaciones [ editar ]

Una operación binaria f en un conjunto S puede verse como una relación ternaria en S , es decir, el conjunto de triples ( a , b , f (a, b) ) en S × S × S para todos a y b en S .

Operaciones binarias externas [ editar ]

Un externa operación binaria es una función binaria de K × S a S . Esto difiere de una operación binaria en el sentido estricto en que K no necesita ser S ; Sus elementos provienen del exterior .

Un ejemplo de una operación binaria externa es la multiplicación escalar en álgebra lineal . Aquí K es un campo y S es un espacio vectorial sobre ese campo.

Una operación binaria externa puede verse alternativamente como una acción ; K está actuando en S .

Tenga en cuenta que el producto escalar de dos vectores no es una operación binaria, externa o de otro modo, ya que los mapas de S × S a K , donde K es un campo y S es un espacio vectorial sobre K .

Una operación binaria $${\ displaystyle \ circ} Es un cálculo que combina los argumentos. $${\ displaystyle x} y $${\ displaystyle y} a $${\ displaystyle x \ circ y}

 cierra bajo una operación si el rendimiento de esa operación en miembros del conjunto siempre produce un miembro de ese conjunto. Por ejemplo, los enteros positivos se cierran por adición, pero no por sustracción:$${\ displaystyle 1-2}no es un entero positivo aunque ambos 1 y 2 sean enteros positivos. Otro ejemplo es el conjunto que contiene solo cero, que se cierra bajo suma, resta y multiplicación (porque$${\ displaystyle 0 + 0 = 0}, $${\ displaystyle 0-0 = 0}y $${\ displaystyle 0 \ times {0} = 0}).

De manera similar, se dice que un conjunto se cierra bajo una colección de operaciones si se cierra individualmente bajo cada una de las operaciones.

Propiedades basicas [ editar ]

Se dice que un conjunto que se cierra bajo una operación o colección de operaciones satisface una propiedad de cierre . A menudo, una propiedad de cierre se introduce como un axioma , que generalmente se denomina axioma de cierre . Las definiciones modernas de la teoría de conjuntos generalmente definen las operaciones como mapas entre conjuntos, por lo que agregar un cierre a una estructura como un axioma es superfluo; sin embargo, en la práctica, las operaciones a menudo se definen inicialmente en un superconjunto del conjunto en cuestión y se requiere una prueba de cierre para establecer que la operación aplicada a pares de ese conjunto solo produce miembros de ese conjunto. Por ejemplo, el conjunto de enteros pares se cierra bajo adición, pero el conjunto de enteros impares no lo está.

Cuando un conjunto S no está cerrado en algunas operaciones, generalmente se puede encontrar el conjunto más pequeño que contiene S que está cerrado. Este conjunto cerrado más pequeño se llama cierre de S (con respecto a estas operaciones). Por ejemplo, el cierre bajo la resta del conjunto de números naturales, visto como un subconjunto de los números reales, es el conjunto de enteros . Un ejemplo importante es el del cierre topológico . La noción de cierre está generalizada por la conexión de Galois , y más adelante por mónadas .

El conjunto S debe ser un subconjunto de un conjunto cerrado para que se defina el operador de cierre. En el ejemplo anterior, es importante que los reales se cierren bajo la resta; en el dominio de los números naturales no siempre se define la resta.

Los dos usos de la palabra "cierre" no deben confundirse. El primer uso se refiere a la propiedad de estar cerrado, y el último se refiere al conjunto cerrado más pequeño que contiene uno que no se puede cerrar. En resumen, el cierre de un conjunto satisface una propiedad de cierre.

Conjuntos cerrados [ editar ]

Un conjunto se cierra en una operación si la operación devuelve un miembro del conjunto cuando se evalúa en los miembros del conjunto. A veces, el requisito de que la operación se valore en un conjunto se establece explícitamente, en cuyo caso se conoce como el axioma de cierre . Por ejemplo, uno puede definir un grupocomo un conjunto con un operador de producto binario que obedece a varios axiomas, incluido el axioma de que el producto de cualquiera de los dos elementos del grupo es nuevamente un elemento. Sin embargo, la definición moderna de una operación hace que este axioma sea superfluo; un n ary operación en S es sólo un subconjunto de S ^n 1 . Por su propia definición, un operador en un conjunto no puede tener valores fuera del conjunto.

Sin embargo, la propiedad de cierre de un operador en un conjunto todavía tiene alguna utilidad. El cierre en un conjunto no implica necesariamente el cierre en todos los subconjuntos. Así, un subgrupo de un grupo es un subconjunto en el que el producto binario y la operación unaria de inversión satisfacen el axioma de cierre.

Una operación de un tipo diferente es la de encontrar los puntos límite de un subconjunto de un espacio topológico (si el espacio es el primero contable , basta con restringir la consideración a los límites de las secuencias, pero en general se deben considerar al menos los límites de las redes). ). Un conjunto que se cierra en esta operación generalmente se conoce como un conjunto cerrado en el contexto de la topología . Sin ninguna calificación adicional, la frase generalmente significa cerrado en este sentido. Intervalos cerrados como [1,2] = { x  : 1 ≤ x ≤ 2} están cerrados en este sentido.

Un conjunto parcialmente ordenado se cierra hacia abajo (y también se llama un conjunto inferior ) si para cada elemento del conjunto también hay todos los elementos más pequeños; esto se aplica, por ejemplo, para los intervalos reales (−∞,  p ) y (−∞,  p ], y para un número ordinal p representado como intervalo [0,  p ); Cada conjunto cerrado a la baja de números ordinales es en sí mismo un número ordinal.

Los conjuntos hacia arriba cerrados y superiores se definen de manera similar.

Ejemplos [ editar ]

• En topología y ramas relacionadas, la operación relevante está tomando límites. El cierre topológico de un conjunto es el operador de cierre correspondiente. Los axiomas de cierre de Kuratowski caracterizan a este operador.
• En álgebra lineal , el tramo lineal de un conjunto X de vectores es el cierre de ese conjunto; es el subconjunto más pequeño del espacio vectorial que incluye X y se cierra bajo la operación de combinación lineal . Este subconjunto es un subespacio .
• En matroide teoría, el cierre de X es el mayor superconjunto de X que tiene el mismo rango que X .
• En la teoría de conjuntos , el cierre transitivo de un conjunto .
• En la teoría de conjuntos , el cierre transitivo de una relación binaria .
• En álgebra , el cierre algebraico de un campo .
• En álgebra conmutativa , operaciones de cierre por ideales, como cierre integral y cierre hermético .
• En geometría , el casco convexo de un conjunto S de puntos es el conjunto convexo más pequeño del cual Ses un subconjunto .
• En los lenguajes formales , el cierre de Kleene de un lenguaje se puede describir como el conjunto de cadenas que se pueden realizar al concatenar cero o más cadenas de ese idioma.
• En teoría de grupos , el cierre conjugado o el cierre normal de un conjunto de elementos de grupo es el subgrupo normal más pequeño que contiene el conjunto.
• En el análisis matemático y en la teoría de la probabilidad , el cierre de una colección de subconjuntos de Xbajo muchas operaciones de conjuntos se denomina σ-álgebra generada por la colección.

Operador de cierre [ editar ]

Artículo principal: operador de cierre

Dada una operación en un conjunto X , se puede definir el cierre C ( S ) de un subconjunto S de X para que sea el subconjunto más pequeño cerrado en esa operación que contiene S como un subconjunto, si existe alguno de estos subconjuntos. En consecuencia, C ( S ) es la intersección de todos los conjuntos cerrados que contienen S. Por ejemplo, el cierre de un subconjunto de un grupo es el subgrupo generado por ese conjunto.

El cierre de los conjuntos con respecto a alguna operación define un operador cierre en los subconjuntos de X . Los conjuntos cerrados pueden ser determinados por el operador de cierre; un conjunto se cierra si es igual a su propio cierre. Las propiedades estructurales típicas de todas las operaciones de cierre son: ^[1]

• El cierre es creciente o extenso : el cierre de un objeto contiene el objeto.
• El cierre es idempotente : el cierre del cierre es igual al cierre.
• El cierre es monótono , es decir, si X está contenido en Y , entonces C ( X ) está contenido en C ( Y ).

Un objeto que es su propio cierre se llama cerrado . Por idempotencia, un objeto se cierra si y solo si es el cierre de algún objeto.

Estas tres propiedades definen un operador de cierre abstracto . Normalmente, un cierre abstracto actúa sobre la clase de todos los subconjuntos de un conjunto.

Si X está contenido en un conjunto cerrado bajo la operación, entonces cada subconjunto de X tiene un cierre.

Cierres relación binaria [ editar ]

Consideremos en primer lugar las relaciones homogéneas R ⊆ A × A . Si una relación S satisface aSb ⇒ bSa , entonces es una relación simétrica . Una relación homogénea arbitraria R puede no ser simétrica pero siempre está contenida en alguna relación simétrica: R ⊆ S . La operación de encontrar la más pequeña tales Scorresponde a un operador de llamada de cierre clausura simétrica .

Una relación transitiva T satisface aTb ∧ bTc ⇒ aTc . Una relación homogénea arbitraria R puede no ser transitiva pero siempre está contenida en alguna relación transitiva: R ⊆ T . La operación de encontrar la más pequeñatales T corresponde a un operador de cierre denominado cierre transitivo .

Entre las relaciones heterogéneas hay propiedades de difuncionalidad y contacto que conducen al cierre difuncional y al cierre por contacto . ^[2] La presencia de estos operadores de cierre en las relaciones binarias conduce a la topología ya que los axiomas de conjunto abierto pueden ser reemplazados por los axiomas de cierre de Kuratowski . Por lo tanto, cada propiedad P , simetría, transitividad, difuncionalidad o contacto corresponde a una topología relacional. ^[3]

En la teoría de los sistemas de reescritura , a menudo se utilizan nociones más verbales como el cierre transitivo reflexivo R ^*: el preorden más pequeño que contiene R , o el cierre simétrico transitivo reflexivo R ^≡ , la relación de equivalencia más pequeña que contiene R , y por lo tanto también se conoce como cierre de equivalencia . Cuando se considera un término particular de álgebra , una relación de equivalencia que es compatible con todas las operaciones del álgebra ^{[nota 1]} se denomina relación de congruencia . El cierre de congruencia.de R se define como la relación de congruencia más pequeño que contiene R .

Para P y R arbitrarios , el cierre de P de R no necesita existir. En los ejemplos anteriores, estos existen porque la reflexividad, la transitividad y la simetría están cerradas en intersecciones arbitrarias. En tales casos, el P de cierre puede estar directamente define como la intersección de todos los conjuntos con propiedad P que contiene R . ^[4]

Algunos cierres particulares importantes pueden obtenerse constructivamente de la siguiente manera:

• cl _ref ( R ) = R ∪ {⟨ x , x ⟩: x ∈ S } es la clausura reflexiva de R ,
• cl _sym ( R ) = R ∪ {⟨ y , x ⟩: ⟨ x , y ⟩ ∈ R } es su cierre simétrica,
• cl _trn ( R ) = R ∪ {⟨ x ₁ , x _n ⟩: n > 1 ∧ ⟨ x ₁ , x ₂ ⟩, ..., ⟨ x _n -1 , x _n ⟩ ∈ R } es su cierre transitivo ,
• cl _{emb, Σ} ( R ) = R ∪ {⟨ f ( x ₁ , ..., x _i -1 , x _i , x _i 1 , ..., x _n ), f ( x ₁ , ..., x _i -1 , y , x _i 1 , ..., x _n )⟩: ⟨ x _i , y ⟩ ∈ R ∧ f ∈ Σ n ary ∧ 1 ≤ i ≤n ∧ x ₁ , ..., x _n ∈ S } es su cierre de incrustación con respecto a un conjunto dado de operaciones en S , cada una con una aridad fija.

Se dice que la relación R tiene un cierre bajo algún cl _xxx , si R = cl _xxx ( R ); por ejemplo, R se llama simétrico si R = cl _sym ( R ).

Cualquiera de estos cuatro cierres conserva la simetría, es decir, si R es simétrico, también lo es cualquier cl _xxx ( R ). ^{[nota 2]} Del mismo modo, los cuatro conservan la reflexividad. Además, cl _trn conserva el cierre bajo cl _{emb, Σ}para arbitrario Σ. Como consecuencia, el cierre de equivalencia de una relación binaria arbitraria R se puede obtener como cl _trn ( cl _sym ( cl _ref ( R ))), y el cierre de congruencia con respecto a algunos Σ se puede obtener como cl _trn ( cl _{emb, Σ}( cl _sym ( cl _ref ( R )))). En este último caso, el orden de anidación sí importa. por ejemplo, si Ses el conjunto de términos más Σ = { a , b , c , f } y R = {⟨ un , b ⟩, ⟨ f ( b ), c ⟩}, entonces el par ⟨ f ( un ), c ⟩ Está contenido en el cierre de congruencia cl _trn ( cl _{emb, Σ} ( cl _sym ( cl_ref ( R ))) de R , pero no en la relación cl _{emb, Σ} ( cl _trn ( cl _sym ( cl _ref ( R )))).

propiedad asociativa ^[1] es una propiedad de algunas operaciones binarias . En lógica proposicional , la asociatividad es una regla válida de reemplazo para expresionesen pruebas lógicas .

Dentro de una expresión que contiene dos o más apariciones en una fila del mismo operador asociativo, el orden en el que se realizan las operaciones no importa siempre que no se cambie la secuencia de los operandos . Es decir, reorganizar los paréntesisen dicha expresión no cambiará su valor. Considera las siguientes ecuaciones:

$${\ displaystyle (2 + 3) + 4 = 2 + (3 + 4) = 9 \,}

$${\ displaystyle 2 \ times (3 \ times 4) = (2 \ times 3) \ times 4 = 24.}

Aunque los paréntesis se reorganizaron en cada línea, los valores de las expresiones no se alteraron. Dado que esto es cierto cuando se realizan sumas y multiplicaciones en cualquier número real , se puede decir que "la suma y multiplicación de números reales son operaciones asociativas".

La asociatividad no es lo mismo que la conmutatividad , que trata si el orden de dos operandos cambia o no el resultado. Por ejemplo, el orden no importa en la multiplicación de números reales, es decir, a × b = b × a , por lo que decimos que la multiplicación de números reales es una operación conmutativa.

Las operaciones asociativas son abundantes en matemáticas; de hecho, muchas estructuras algebraicas (como semigrupos y categorías ) requieren explícitamente que sus operaciones binarias sean asociativas.

Sin embargo, muchas operaciones importantes e interesantes son no asociativas; algunos ejemplos incluyen la resta , la exponenciación y el producto cruzado vectorial . En contraste con las propiedades teóricas de los números reales, la adición de números de punto flotante en informática no es asociativa, y la elección de cómo asociar una expresión puede tener un efecto significativo en el error de redondeo.

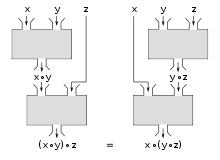
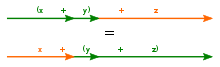
Formalmente, una operación binaria ∗ en un conjunto S se llama asociativa si cumple con la ley asociativa :

( X * y ) * z = x * ( y * z ) para todo x , y , z en S .

Aquí, ∗ se usa para reemplazar el símbolo de la operación, que puede ser cualquier símbolo, e incluso la ausencia de símbolo ( yuxtaposición ) como para la multiplicación .

( Xy ) z = x ( yz ) = xyz para todos x , y , z en S .

La ley asociativa también puede expresarse en notación funcional por lo tanto: f ( f ( x , y ), z ) = f ( x , f ( y , z )) .

Ley asociativa generalizada [ editar ]

En ausencia de la propiedad asociativa, cinco factores a, b, c, d, e resultan en una red Tamari de orden cuatro, posiblemente productos diferentes.

Si una operación binaria es asociativa, la aplicación repetida de la operación produce el mismo resultado, independientemente de cómo se inserten pares de paréntesis válidos en la expresión. ^[2]Esto se llama la ley asociativa generalizada . Por ejemplo, un producto de cuatro elementos puede escribirse de cinco maneras posibles:

1. ((a B C D
2. (a B C D)
3. (a B C D
4. a B C D)
5. a B C D))

Si la operación del producto es asociativa, la ley asociativa generalizada dice que todas estas fórmulas darán el mismo resultado, haciendo que el paréntesis sea innecesario. Así, "el" producto se puede escribir de forma inequívoca como

a B C D.

A medida que aumenta el número de elementos, el número de formas posibles de insertar paréntesis crece rápidamente, pero siguen siendo innecesarios para la desambiguación.

Ejemplos [ editar ]

En operaciones asociativas es $${\ displaystyle (x \ circ y) \ circ z = x \ circ (y \ circ z)}.

La suma de números reales es asociativa.

Algunos ejemplos de operaciones asociativas incluyen los siguientes.

• La concatenación de las tres cadenas "hello", " ", "world"se puede calcular mediante la concatenación de las dos primeras cuerdas (dar "hello ") y añadiendo la tercera cuerda ( "world"), o uniéndose a la segunda y tercera cuerda (dar " world") y la concatenación de la primera cadena ( "hello") con el resultado. Los dos métodos producen el mismo resultado; La concatenación de cadenas es asociativa (pero no conmutativa).
• En aritmética , la suma y la multiplicación de números reales son asociativas; es decir,

$${\ displaystyle \ left. {\ begin {matrix} (x + y) + z = x + (y + z) = x + y + z \ quad \\ (x \, y) z = x (y \, z ) = x \, y \, z \ qquad \ qquad \ qquad \ quad \ \ \, \ end {matrix}} \ right \} {\ mbox {para todos}} x, y, z \ in \ mathbb {R }.}

Debido a la asociatividad, los paréntesis de agrupación pueden omitirse sin ambigüedad.

• La operación trivial x ∗ y = x (es decir, el resultado es el primer argumento, sin importar cuál sea el segundo argumento) es asociativa pero no conmutativa. Del mismo modo, la operación trivial x ∘ y = y (es decir, el resultado es el segundo argumento, sin importar cuál sea el primer argumento) es asociativa pero no conmutativa.
• La suma y multiplicación de números complejos y cuaterniones son asociativos. La adición de octonionestambién es asociativa, pero la multiplicación de octoniones no es asociativa.
• El mayor divisor común y las funciones múltiples menos comunes actúan de manera asociativa.

$${\ displaystyle \ left. {\ begin {matrix} \ operatorname {gcd} (\ operatorname {gcd} (x, y), z) = \ operatorname {gcd} (x, \ operatorname {gcd} (y, z) ) = \ operatorname {gcd} (x, y, z) \ \ quad \\\ operatorname {lcm} (\ operatorname {lcm} (x, y), z) = \ operatorname {lcm} (x, \ operatorname { lcm} (y, z)) = \ operatorname {lcm} (x, y, z) \ quad \ end {matrix}} \ right \} {\ mbox {para todos}} x, y, z \ in \ mathbb {Z}.}

• Tomando la intersección o la unión de conjuntos :

$${\ displaystyle \ left. {\ begin {matrix} (A \ cap B) \ cap C = A \ cap (B \ cap C) = A \ cap B \ cap C \ quad \\ (A \ cup B) \ cup C = A \ cup (B \ cup C) = A \ cup B \ cup C \ quad \ end {matrix}} \ right \} {\ mbox {para todos los conjuntos}} A, B, C.}

• Si M es un conjunto y S denota el conjunto de todas las funciones de M a M , entonces la operación de la composición de la función en S es asociativa:

$${\ displaystyle (f \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h \ qquad {\ mbox {para todos}} f, g, h \ en S.}

• Un poco más generalmente, dados cuatro conjuntos M , N , P y Q , con h : M a N , g : N a P , y f : P a Q , entonces

$${\ displaystyle (f \ circ g) \ circ h = f \ circ (g \ circ h) = f \ circ g \ circ h}

como antes. En resumen, la composición de los mapas es siempre asociativa.

• Considere un conjunto con tres elementos, A, B y C. La siguiente operación:

×	UNA	segundo	do
UNA	UNA	UNA	UNA
segundo	UNA	segundo	do
do	UNA	UNA	UNA

es asociativa Así, por ejemplo, A (BC) = (AB) C = A. Esta operación no es conmutativa.

• Debido a que las matrices representan funciones lineales y la multiplicación de matrices representa la composición de funciones, uno puede concluir inmediatamente que la multiplicación de matrices es asociativa. ^[3]

La lógica proposicional [ editar ]

Regla de reemplazo [ editar ]

En la lógica proposicional funcional de verdad estándar, asociación , ^[4] [5] o asociatividad ^[6] son dos reglas válidas de reemplazo . Las reglas permiten mover paréntesis en expresiones lógicas en pruebas lógicas . Las reglas (usando notación de conectivas lógicas ) son:

$${\ displaystyle (P \ lor (Q \ lor R)) \ Leftrightarrow ((P \ lor Q) \ lor R)}

y

$${\ displaystyle (P \ land (Q \ land R)) \ Leftrightarrow ((P \ land Q) \ land R),}

dónde "$${\ displaystyle \ Leftrightarrow}"es un símbolo metalógico que representa" se puede reemplazar en una prueba con ".

Conectivos funcionales de la verdad [ editar ]

La asociatividad es una propiedad de algunos conectivos lógicos de la lógica proposicional funcional a la verdad . Las siguientes equivalencias lógicas demuestran que la asociatividad es una propiedad de conectivos particulares. Las siguientes son tautologías de verdad funcional .

Asociatividad de la disyunción .

$${\ displaystyle ((P \ lor Q) \ lor R) \ leftrightarrow (P \ lor (Q \ lor R))}

$${\ displaystyle (P \ lor (Q \ lor R)) \ leftrightarrow ((P \ lor Q) \ lor R)}

Asociatividad de conjunción :

$${\ displaystyle ((P \ land Q) \ land R) \ leftrightarrow (P \ land (Q \ land R))}

$${\ displaystyle (P \ land (Q \ land R)) \ leftrightarrow ((P \ land Q) \ land R)}

Asociatividad de equivalencia :

$${\ displaystyle ((P \ leftrightarrow Q) \ leftrightarrow R) \ leftrightarrow (P \ leftrightarrow (Q \ leftrightarrow R))}

$${\ displaystyle (P \ leftrightarrow (Q \ leftrightarrow R)) \ leftrightarrow ((P \ leftrightarrow Q) \ leftrightarrow R)}

La negación conjunta es un ejemplo de un conectivo funcional de verdad que no es asociativo.

Operación no asociativa [ editar ]

Una operación binaria $${\ displaystyle *}en un conjunto S que no cumple con la ley asociativa se llama no asociativo . Simbólicamente,

$${\ displaystyle (x * y) * z \ neq x * (y * z) \ qquad {\ mbox {para algunos}} x, y, z \ en S.}

Para tal operación, el orden de evaluación sí importa. Por ejemplo:

• Sustracción

$${\ displaystyle (5-3) -2 \, \ neq \, 5- (3-2)}

• División

$${\ displaystyle (4/2) / 2 \, \ neq \, 4 / (2/2)}

• Exposiciónción

$${\ displaystyle 2 ^ {(1 ^ {2})} \, \ neq \, (2 ^ {1}) ^ {2}}

También tenga en cuenta que las sumas infinitas no son generalmente asociativas, por ejemplo:

$${\ displaystyle (1 + -1) + (1 + -1) + (1 + -1) + (1 + -1) + (1 + -1) + (1 + -1) + \ dots \, = \, 0}

mientras

$${\ displaystyle 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + \ dots \ , = \, 1}

El estudio de las estructuras no asociativas surge por razones algo diferentes de la corriente principal del álgebra clásica. Un área dentro del álgebra no asociativa que ha crecido mucho es la de álgebras de Lie . Allí la ley asociativa es reemplazada por la identidad jacobi . Las álgebras de la mentira resumen la naturaleza esencial de las transformaciones infinitesimales y se han vuelto omnipresentes en las matemáticas.

Existen otros tipos específicos de estructuras no asociativas que se han estudiado en profundidad; estos tienden a provenir de algunas aplicaciones específicas o áreas como las matemáticas combinatorias . Otros ejemplos son cuasigrupo , Quasifield , anillo no asociativo , álgebra no asociativo y magmas no asociativos conmutativos .

Nonassociativity de cálculo de punto flotante [ editar ]

En matemáticas, la suma y multiplicación de números reales es asociativa. Por el contrario, en informática, la suma y multiplicación de números de punto flotante no es asociativa, ya que los errores de redondeo se introducen cuando se unen valores de tamaño diferente. ^[7]

Para ilustrar esto, considere una representación de punto flotante con una mantisa de 4 bits: 
(1.000 ₂ × 2 ⁰ + 1.000 ₂ × 2 ⁰ ) + 1.000 ₂ × 2 ⁴ = 1.000 ₂ × 2 ¹ + 1.000 ₂ × 2 ⁴ = 1.00 1 ₂ × 2 ⁴
1.000 ₂ × 2 ⁰ + (1.000 ₂ × 2 ⁰ + 1.000 ₂ × 2 ⁴ ) = 1.000 ₂ × 2 ⁰ + 1.00 0 ₂ × 2 ⁴ = 1.00 0₂ × 2 ⁴

Aunque la mayoría de las computadoras calculan con 24 o 53 bits de mantisa, ^[8] esta es una fuente importante de error de redondeo, y los enfoques como el algoritmo de suma Kahan son formas de minimizar los errores. Puede ser especialmente problemático en la computación paralela. ^[9] [10]

Notación para operaciones no asociativas [ editar ]

Artículo principal: asociatividad de operadores

En general, los paréntesis deben usarse para indicar el orden de evaluación si una operación no asociativa aparece más de una vez en una expresión. Sin embargo, los matemáticos acuerdan un orden particular de evaluación para varias operaciones comunes no asociativas. Esto es simplemente una convención de notación para evitar paréntesis.

Una operación asociativa a la izquierda es una operación no asociativa que se evalúa convencionalmente de izquierda a derecha, es decir,

$${\ displaystyle \ left. {\ begin {matrix} x * y * z = (x * y) * z \ qquad \ qquad \ quad \, \\ w * x * y * z = ((w * x) * y) * z \ quad \\ {\ mbox {etc.}} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix}} \ right \} {\ mbox {para todos}} w, x, y, z \ en S}

mientras que una operación asociativa por la derecha se evalúa convencionalmente de derecha a izquierda:

$${\ displaystyle \ left. {\ begin {matrix} x * y * z = x * (y * z) \ qquad \ qquad \ quad \, \\ w * x * y * z = w * (x * (y * z)) \ quad \\ {\ mbox {etc.}} \ qquad \ qquad \ qquad \ qquad \ qquad \ qquad \ \ \, \ end {matrix}} \ right \} {\ mbox {para todos}} w, x, y, z \ en S}

Ocurren operaciones tanto asociativas por la izquierda como asociativas por la derecha. Las operaciones asociativas por la izquierda incluyen lo siguiente:

• Resta y división de números reales: ^{[11] [12] [13] [14] [15]}

$${\ displaystyle xyz = (xy) -z}

$${\ displaystyle x / y / z = (x / y) / z}

• Aplicación de la función:

$${\ displaystyle (f \, x \, y) = ((f \, x) \, y)}

Esta notación puede ser motivada por el isomorfismo del curry .

Las operaciones asociativas por derecho incluyen lo siguiente:

• Exposición de números reales:

$${\ displaystyle x ^ {y ^ {z}} = x ^ {(y ^ {z})}}

Una razón por la que la exponenciación es asociativa a la derecha es que una operación repetitiva de exponenciación asociativa a la izquierda sería menos útil. Las apariencias múltiples podrían (y serían) reescritas con la multiplicación:

$${\ displaystyle (x ^ {y}) ^ {z} = x ^ {(yz)}}

Un argumento adicional para que la exponenciación sea asociativa a la derecha es que el superíndice se comporta inherentemente como un conjunto de paréntesis; por ejemplo, en la expresión$${\ displaystyle 2 ^ {x + 3}}la adición se realiza antes de la exponencia a pesar de que no haya paréntesis explícitos$${\ displaystyle 2 ^ {(x + 3)}}Envuelto alrededor de él. Así dada una expresión tal como$${\ displaystyle x ^ {y ^ {z}}}, tiene sentido requerir evaluar el exponente completo $${\ displaystyle y ^ {z}} de la base $${\ displaystyle x}primero.

• Tetración a través del operador de flecha arriba :

$${\ displaystyle a \ uparrow \ uparrow b = \, ^ {b} a}

• Definición de la función

$${\ displaystyle \ mathbb {Z} \ rightarrow \ mathbb {Z} \ rightarrow \ mathbb {Z} = \ mathbb {Z} \ rightarrow (\ mathbb {Z} \ rightarrow \ mathbb {Z})}

$${\ displaystyle x \ mapsto y \ mapsto xy = x \ mapsto (y \ mapsto xy)}

El uso de la notación asociativa correcta para estas operaciones puede estar motivado por la correspondencia de Curry-Howard y por el isomorfismo del curry .

Las operaciones no asociativas para las cuales no se define un orden de evaluación convencional incluyen lo siguiente.

• Tomando el producto cruzado de tres vectores:

$${\ displaystyle {\ vec {a}} \ times ({\ vec {b}} \ times {\ vec {c}}) \ neq ({\ vec {a}} \ times {\ vec {b}}) \ times {\ vec {c}} \ qquad {\ mbox {para algunos}} {\ vec {a}}, {\ vec {b}}, {\ vec {c}} \ in \ mathbb {R} ^ {3}}

• Tomando el promedio por pares de los números reales:

$${\ displaystyle {(x + y) / 2 + z \ sobre 2} \ neq {x + (y + z) / 2 \ sobre 2} \ qquad {\ mbox {para todos}} x, y, z \ in \ mathbb {R} {\ mbox {con}} x \ neq z.}

• Tomando el complemento relativo de conjuntos.$${\ displaystyle (A \ backslash B) \ backslash C} no es lo mismo que $${\ displaystyle A \ backslash (B \ backslash C)}. (Comparar material no implícito en lógica.)