MECÁNICA CLÁSICA

materiales con memoria , también conocidos como materiales con efectos hereditarios, son una clase de materiales cuyas ecuaciones constitutivas dependen de la historia pasada de las variables de estado termodinámicas, cinéticas , electromagnéticas o de otro tipo .

Notas históricas [ editar ]

El estudio de estos materiales surge de los artículos pioneros de Ludwig Boltzmann ^[1] [2] y Vito Volterra , ^[3] [4] en los que buscaron una extensión del concepto de un material elástico . ^[5] El supuesto clave de su teoría era que el valor del estrés local en un momento t depende de la historia de la deformación local hasta t . En general, en materiales con memoria el valor local de alguna cantidad constitutiva (tensión, flujo de calor, corriente eléctrica, polarización y magnetización, etc.) a la vez tDepende de la historia de las variables de estado (deformación, temperatura, campos eléctricos y magnéticos, etc.). La hipótesis de que la historia remota de una variable tiene menos influencia que sus valores en el pasado reciente, se estableció en la mecánica de continuidad moderna como el principio de la memoria de desvanecimiento por Bernard Coleman y Walter Noll . Este supuesto estaba implícito en los trabajos pioneros: cuando se restringe a las historias cíclicas, se remonta al principio de ciclo cerrado establecido por Volterra, ^[4] que se relaciona con una relación constitutiva de tipo de convolución integral. En el caso lineal, esta relación toma la forma de una ecuación de Volterra.

Relaciones constitutivas de materiales con memoria [ editar ]

En el caso lineal, esta relación toma la forma de una ecuación de Volterra.

$${\ displaystyle {\ boldsymbol {T}} ({\ boldsymbol {x}}, t) = {\ boldsymbol {G}} _ {0} ({\ boldsymbol {x}}) {\ boldsymbol {E}} ( {\ boldsymbol {x}}, t) + \ int _ {0} ^ {+ \ infty} \! \! \! \! boldsymbol {G}} ^ {\ prime} ({\ boldsymbol {x} }, s) {\ boldsymbol {E}} ({\ boldsymbol {x}}, ts) \ mathrm {d} s}

En el marco de referencia inercial (parte superior de la imagen), la bola negra se mueve en línea recta. Sin embargo, el observador (punto marrón) que se encuentra en el marco de referencia giratorio / no inercial (parte inferior de la imagen) ve al objeto siguiendo una trayectoria curva debido a las fuerzas de Coriolis y centrífugas presentes en este marco.

En física , la fuerza de Coriolis es una fuerza inercial o ficticia ^[1] que parece actuar sobre objetos que están en movimiento dentro de un marco de referencia que gira con respecto a un marco inercial. En un marco de referencia con rotación en el sentido de las agujas del reloj , la fuerza actúa a la izquierda del movimiento del objeto. En una con rotación en sentido contrario a las agujas del reloj (o en sentido contrario a las agujas del reloj), la fuerza actúa hacia la derecha. La deflexión de un objeto debido a la fuerza de Coriolis se denomina efecto de Coriolis . Aunque previamente reconocido por otros, la expresión matemática de la fuerza de Coriolis apareció en un artículo de 1835 del científico francés Gaspard-Gustave de Coriolis., en relación con la teoría de las ruedas hidráulicas . A principios del siglo XX, el término fuerza de Coriolis comenzó a usarse en relación con la meteorología .

Las leyes de movimiento de Newton describen el movimiento de un objeto en un marco de referencia inercial (no acelerante) . Cuando las leyes de Newton se transforman en un marco de referencia giratorio, aparecen la fuerza de Coriolis y la fuerza centrífuga . Ambas fuerzas son proporcionales a la masa.del objeto. La fuerza de Coriolis es proporcional a la velocidad de rotación y la fuerza centrífuga es proporcional al cuadrado de la velocidad de rotación. La fuerza de Coriolis actúa en una dirección perpendicular al eje de rotación ya la velocidad del cuerpo en el marco giratorio y es proporcional a la velocidad del objeto en el marco giratorio (más precisamente, a la componente de su velocidad que es perpendicular al eje de rotación). La fuerza centrífuga actúa hacia afuera en la dirección radial y es proporcional a la distancia del cuerpo desde el eje del bastidor giratorio. Estas fuerzas adicionales se denominan fuerzas inerciales, fuerzas ficticias o pseudo fuerzas . ^[2]Permiten la aplicación de las leyes de Newton a un sistema rotativo. Son factores de corrección que no existen en un marco de referencia inercial o no acelerante.

En el uso popular (no técnico) del término "efecto Coriolis", el marco de referencia giratorio implícito es casi siempre la Tierra. Debido a que la Tierra gira, los observadores ligados a la Tierra deben tener en cuenta la fuerza de Coriolis para analizar correctamente el movimiento de los objetos. La Tierra completa una rotación por día, por lo que para los movimientos de los objetos cotidianos, la fuerza de Coriolis suele ser bastante pequeña en comparación con otras fuerzas; sus efectos generalmente se hacen notorios solo por movimientos que se producen en grandes distancias y largos períodos de tiempo, como el movimiento de aire a gran escala en la atmósfera o el agua en el océano. Tales movimientos están limitados por la superficie de la Tierra, por lo que solo el componente horizontal de la fuerza de Coriolis es generalmente importante. Esta fuerza hace que los objetos en movimiento en la superficie de la Tierra se desvíen hacia la derecha (con respecto a la dirección de desplazamiento) en el hemisferio norte y hacia la izquierda en el hemisferio sur. El efecto de deflexión horizontal es mayor cerca de los polos , ya que la tasa de rotación efectiva sobre un eje vertical local es mayor allí y disminuye a cero en el ecuador . ^[3] En lugar de fluir directamente desde áreas de alta presión a baja presión, como lo harían en un sistema no giratorio, los vientos y las corrientes tienden a fluir a la derecha de esta dirección al norte del ecuador y a la izquierda de esta dirección al sur de eso Este efecto es responsable de la rotación de ciclones grandes (consulte Efectos de Coriolis en meteorología ).

Para una explicación intuitiva del origen de la fuerza de Coriolis, considere un objeto, obligado a seguir la superficie de la Tierra y moviéndose hacia el norte en el hemisferio norte. Visto desde el espacio exterior, el objeto no parece ir hacia el norte, pero tiene un movimiento hacia el este (gira alrededor de la derecha junto con la superficie de la Tierra). Cuanto más al norte se vaya, menor será el "diámetro horizontal" de la Tierra (la distancia mínima desde el punto de la superficie hasta el eje de rotación, que está en un plano ortogonal al eje), y por lo tanto, más lento será el movimiento hacia el este de su superficie. A medida que el objeto se mueve hacia el norte, a latitudes más altas, tiene una tendencia a mantener la velocidad hacia el este con la que comenzó (en lugar de reducir la velocidad para igualar la velocidad reducida hacia el este de los objetos locales en la superficie de la Tierra), por lo que gira al este (es decir,^[4] [5] Aunque no es obvio en este ejemplo, que considera el movimiento hacia el norte, la desviación horizontal se produce por igual para los objetos que se mueven hacia el este o el oeste (o cualquier otra dirección).

Historia [ editar ]

Imagen de Cursus seu Mundus Mathematicus (1674) de CFM Dechales, que muestra cómo una bola de cañón debe desviarse hacia la derecha de su objetivo en una Tierra giratoria, porque el movimiento hacia la derecha de la bola es más rápido que el de la torre.

Imagen de Cursus seu Mundus Mathematicus (1674) de CFM Dechales, que muestra cómo debería caer una bola desde una torre en una Tierra en rotación. El balón se lanza desde f . La parte superior de la torre se mueve más rápido que su base, por lo que mientras la bola cae, la base de la torre se mueve hacia I , pero la bola, que tiene la velocidad hacia el este de la parte superior de la torre, supera la base de la torre y aterriza más hacia el este. en l .

El científico italiano Giovanni Battista Riccioli y su asistente Francesco Maria Grimaldi describieron el efecto en relación con la artillería en el Almagestum Novum de 1651 , escribiendo que la rotación de la Tierra debería causar que una bala de cañón disparada hacia el norte se desvíe hacia el este. ^[7] En 1674, Claude François Milliet Dechalesdescribió en su Cursus seu Mundus Mathematicus.cómo la rotación de la Tierra debería causar una desviación en las trayectorias de ambos cuerpos en caída y proyectiles dirigidos hacia uno de los polos del planeta. Riccioli, Grimaldi y Dechales describieron el efecto como parte de un argumento en contra del sistema heliocéntrico de Copérnico. En otras palabras, argumentaron que la rotación de la Tierra debería crear el efecto, y por lo tanto, la falla en la detección del efecto fue evidencia de una Tierra inmóvil. ^[8] La ecuación de aceleración de Coriolis fue derivada por Euler en 1749 ^[9] [10] y el efecto se describió en las ecuaciones de marea de Pierre-Simon Laplace en 1778. ^[11]

Gaspard-Gustave Coriolis publicó un documento en 1835 sobre el rendimiento energético de las máquinas con piezas giratorias, como las ruedas hidráulicas . ^[12] Ese documento consideró las fuerzas suplementarias que se detectan en un marco de referencia giratorio. Coriolis dividió estas fuerzas suplementarias en dos categorías. La segunda categoría contenía una fuerza que surge del producto cruzadode la velocidad angular de un sistema de coordenadas y la proyección de la velocidad de una partícula en un plano perpendicular al eje de rotación del sistema . Coriolis se refirió a esta fuerza como la "fuerza centrífuga compuesta" debido a sus analogías con laFuerza centrífuga ya considerada en la categoría uno. ^[13] [14] El efecto fue conocido a principios del siglo 20 como la " aceleración de Coriolis", ^[15] y en 1920 como "fuerza de Coriolis". ^[dieciséis]

En 1856, William Ferrel propuso la existencia de una celda de circulaciónen las latitudes medias, con la fuerza de Coriolis desviando el aire para crear los vientos del oeste que prevalecen . ^[17]

La comprensión de la cinemática de cómo la rotación de la Tierra afecta exactamente al flujo de aire fue parcial al principio. ^{[18] A} finales del siglo XIX, se entendió la magnitud de la interacción a gran escala de la fuerza de gradiente de presión y la fuerza de desviación que al final hace que las masas de aire se muevan a lo largo de las isobaras . ^[19]

Fórmula [ editar ]

Ver también: fuerza ficticia.

En la mecánica newtoniana , la ecuación de movimiento de un objeto en un marco de referencia inercial es

$${\ displaystyle {\ boldsymbol {F}} = m {\ boldsymbol {a}}}

dónde $${\ displaystyle {\ boldsymbol {F}}} es la suma vectorial de las fuerzas físicas que actúan sobre el objeto, $${\ displaystyle m} es la masa del objeto, y $${\ displaystyle {\ boldsymbol {a}}}es la aceleración del objeto en relación con el marco de referencia inercial. Transformar esta ecuación en un marco de referencia no inercial con una tasa de rotación$${\ displaystyle \ omega} Sobre el origen, la ecuación toma la forma.

$${\ displaystyle {\ boldsymbol {F}} - m {\ frac {\ operatorname {d} {\ boldsymbol {\ Omega}}} {\ operatorname {d} t}} \ times {\ boldsymbol {r}} - 2m {\ boldsymbol {\ Omega}} \ times {\ boldsymbol {v '}} - m {\ boldsymbol {\ Omega}} \ times ({\ boldsymbol {\ Omega}} \ times {\ boldsymbol {r}})} $${\ displaystyle = m {\ boldsymbol {a '}}}

dónde

$${\ displaystyle {\ boldsymbol {\ Omega}}} Es el vector de rotación, con magnitud. $${\ displaystyle \ omega}, del marco de referencia giratorio relativo al marco de inercia

$${\ displaystyle {\ boldsymbol {v '}}} es la velocidad relativa al marco de referencia giratorio

$${\ displaystyle {\ boldsymbol {r}}} es el vector de posicion del objeto

$${\ displaystyle {\ boldsymbol {a '}}} es la aceleración relativa al marco de referencia giratorio

Los términos adicionales en el lado de la fuerza de la ecuación son fuerzas ficticias, ya que se perciben en el marco giratorio como fuerzas adicionales que contribuyen a la aceleración aparente, al igual que las fuerzas externas reales. ^[20] [21] Los términos de fuerza ficticia en el lado de la fuerza de la ecuación son, leyendo de izquierda a derecha, la fuerza de Euler $${\ displaystyle -m \ operatorname {d} {\ boldsymbol {\ Omega}} / \ operatorname {d} t \ times {\ boldsymbol {r}}}, la fuerza de Coriolis $${\ displaystyle -2m {\ boldsymbol {\ Omega}} \ times {\ boldsymbol {v '}}}, y la fuerza centrífuga $${\ displaystyle -m {\ boldsymbol {\ Omega}} \ times ({\ boldsymbol {\ Omega}} \ times {\ boldsymbol {r}})}, respectivamente. ^[22] A diferencia de las fuerzas centrífugas y de Euler, que dependen del vector de posición del objeto, la fuerza de Coriolis depende de la velocidad del objeto medida en el marco de referencia giratorio. Como se esperaba, para un marco de referencia inercial no rotativo $${\ displaystyle ({\ boldsymbol {\ Omega}} = 0)}La fuerza de Coriolis y todas las demás fuerzas ficticias desaparecen. ^[23]

Como la fuerza de Coriolis es proporcional a un producto cruzado de dos vectores, es perpendicular a ambos vectores, en este caso la velocidad del objeto y el vector de rotación del marco. Por lo tanto se deduce que:

• Si la velocidad es paralela al eje de rotación, la fuerza de Coriolis es cero. (Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el ecuador que se mueve hacia el norte o hacia el sur en relación con la superficie de la Tierra).
• Si la velocidad es recta hacia el interior del eje, la fuerza de Coriolis es en la dirección de rotación local. (Por ejemplo, en la Tierra, esta situación ocurre cuando un cuerpo en el ecuador cae hacia abajo, como en la ilustración de Dechales arriba, donde la bola que cae viaja más hacia el este que la torre).
• Si la velocidad es recta hacia afuera del eje, la fuerza de Coriolis está en contra de la dirección de rotación local. (En el ejemplo de la torre, una bola lanzada hacia arriba se movería hacia el oeste).
• Si la velocidad está en la dirección de rotación, la fuerza de Coriolis es hacia afuera del eje. (Por ejemplo, en la Tierra, esta situación ocurre para un cuerpo en el ecuador que se mueve hacia el este en relación con la superficie de la Tierra. Se movería hacia arriba como lo ve un observador en la superficie. Este efecto (consulte el efecto de Eötvös a continuación) fue discutido por Galileo Galilei en 1632 y por Riccioli en 1651. ^[24] )
• Si la velocidad es contraria a la dirección de rotación, la fuerza de Coriolis es hacia el interior del eje. (En la Tierra, esta situación ocurre para un cuerpo en el ecuador que se mueve hacia el oeste, lo que se desviaría hacia abajo como lo ve un observador).

Causas [ editar ]

La fuerza de Coriolis existe solo cuando uno usa un marco de referencia giratorio. En el marco giratorio se comporta exactamente como una fuerza real (es decir, causa aceleración y tiene efectos reales). Sin embargo, la fuerza de Coriolis es una consecuencia de la inercia , ^[25] y no es atribuible a un cuerpo originario identificable, como es el caso de las fuerzas electromagnéticas o nucleares, por ejemplo. Desde un punto de vista analítico, para usar la segunda ley de Newton en un sistema rotativo, la fuerza de Coriolis es matemáticamente necesaria, pero desaparece en un marco de referencia inercial no acelerador. Por ejemplo, considere dos niños en lados opuestos de una rotonda giratoria ( Merry-go-round), que están lanzando una pelota entre sí. Desde el punto de vista de los niños, la trayectoria de esta bola está curvada hacia los lados por la fuerza de Coriolis. Supongamos que la rotonda gira en sentido contrario a las agujas del reloj cuando se ve desde arriba. Desde la perspectiva del lanzador, la desviación es hacia la derecha. ^[26] Desde la perspectiva del no lanzador, la desviación es hacia la izquierda. Para una formulación matemática, ver Derivación matemática de fuerzas ficticias . En meteorología, un marco giratorio (la Tierra) con su fuerza de Coriolis proporciona un marco más natural para explicar los movimientos del aire que un marco inercial no giratorio sin fuerzas de Coriolis. ^[27] En la artillería de largo alcance, las correcciones a la vista de la rotación de la Tierra se basan en la fuerza de Coriolis. ^[28] Estos ejemplos se describen con más detalle a continuación.

La aceleración que ingresa a la fuerza de Coriolis surge de dos fuentes de cambio en la velocidad que resultan de la rotación: la primera es el cambio de la velocidad de un objeto en el tiempo. La misma velocidad (en un marco de referencia inercial donde se aplican las leyes normales de la física) se ve como diferentes velocidades en diferentes momentos en un marco de referencia giratorio. La aceleración aparente es proporcional a la velocidad angular del cuadro de referencia (la velocidad a la que los ejes de coordenadas cambian de dirección) y al componente de la velocidad del objeto en un plano perpendicular al eje de rotación. Esto le da un término$${\ displaystyle - {\ boldsymbol {\ Omega}} \ times {\ boldsymbol {v}}}. El signo menos surge de la definición tradicional del producto cruzado ( regla de la mano derecha ) y de la convención de signos para los vectores de velocidad angular.

El segundo es el cambio de velocidad en el espacio. Las diferentes posiciones en un marco de referencia giratorio tienen diferentes velocidades (como se ve desde un marco de referencia inercial). Para que un objeto se mueva en línea recta, debe acelerar de modo que su velocidad cambie de un punto a otro en la misma cantidad que las velocidades del marco de referencia. La fuerza es proporcional a la velocidad angular (que determina la velocidad relativa de dos puntos diferentes en el marco de referencia giratorio), y a la componente de la velocidad del objeto en un plano perpendicular al eje de rotación (que determina qué tan rápido) se mueve entre esos puntos). Esto también da un término$${\ displaystyle - {\ boldsymbol {\ Omega}} \ times {\ boldsymbol {v}}}.

Escalas de longitud y el número de Rossby [ editar ]

Más información: número de Rossby

Las escalas de tiempo, espacio y velocidad son importantes para determinar la importancia de la fuerza de Coriolis. Si la rotación es importante en un sistema se puede determinar por su número de Rossby , que es la relación de la velocidad, U , de un sistema al producto del parámetro Coriolis ,$${\ displaystyle f = 2 \ omega \ sin \ varphi \,}y la escala de longitud, L , del movimiento:

$${\ displaystyle Ro = {\ frac {U} {fL}}.}

El número de Rossby es la relación de inercia a fuerzas de Coriolis. Un pequeño número de Rossby indica que un sistema está fuertemente afectado por las fuerzas de Coriolis, y un gran número de Rossby indica un sistema en el que dominan las fuerzas de inercia. Por ejemplo, en tornados, el número de Rossby es grande, en sistemas de baja presión es bajo y en sistemas oceánicos es alrededor de 1. Como resultado, en tornados la fuerza de Coriolis es insignificante, y el equilibrio es entre presión y fuerzas centrífugas . En los sistemas de baja presión, la fuerza centrífuga es despreciable y el equilibrio está entre Coriolis y las fuerzas de presión. En los océanos las tres fuerzas son comparables. ^[29]

Un sistema atmosférico que se mueve a U  = 10 m / s (22 mph) que ocupa una distancia espacial de L  = 1,000 km (621 mi), tiene un número de Rossby de aproximadamente 0.1.

Un lanzador de béisbol puede lanzar la pelota a U = 45 m / s (100 mph) para una distancia de L = 18.3 m (60 pies). El número de Rossby en este caso sería 32,000.

A los jugadores de béisbol no les importa en qué hemisferio están jugando. Sin embargo, un misil no guiado obedece exactamente a la misma física que una pelota de béisbol, pero puede viajar lo suficientemente lejos y estar en el aire el tiempo suficiente para experimentar el efecto de la fuerza de Coriolis. Los proyectiles de largo alcance en el hemisferio norte aterrizaron cerca, pero a la derecha, hacia donde se apuntaron hasta que esto se notó. (Los disparados en el hemisferio sur aterrizaron a la izquierda). De hecho, fue este efecto el que primero llamó la atención del propio Coriolis. ^{[30] [31] [32]}

Casos sencillos [ editar ]

Esta sección puede ser demasiado larga para leer y navegar cómodamente . Considere la posibilidad de dividir el contenido en sub-artículos, condensarlo o agregar o eliminar subtítulos . ( Marzo de 2014 )

Cañón en la plataforma giratoria [ editar ]

Esta sección puede ser demasiado técnica para que la mayoría de los lectores entiendan . Ayude a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Junio ​​de 2010 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Ver también: Fuerza ficticia § Cruzar un carrusel.

Cañón en el centro de un plato giratorio giratorio. Para golpear el objetivo ubicado en la posición 1 en el perímetro en el tiempo t = 0 s, el cañón debe apuntar por delante del objetivo en el ángulo θ. De esa manera, cuando la bala de cañón alcance la posición 3 en la periferia, el objetivo también estará en esa posición. En un marco de referencia inercial, la bala de cañón recorre una trayectoria radial recta hacia el objetivo (curva y _A ). Sin embargo, en el marco del plato giratorio, la trayectoria está arqueada (curva y _B ), como también se muestra en la figura.

Trayectoria exitosa de bala de cañón vista desde el plato giratorio para tres ángulos de lanzamiento θ. Los puntos trazados son para los mismos pasos espaciados equitativamente en cada curva. La velocidad de bala de cañón v se mantiene constante y la velocidad de rotación angular ω se varía para lograr un "golpe" exitoso para θ seleccionado. Por ejemplo, para un radio de 1 my una velocidad de bala de cañón de 1 m / s, el tiempo de vuelo t _f = 1 s, y ωt _f= θ → ω y θ tienen el mismo valor numérico si θSe expresa en radianes. La separación más amplia de los puntos trazados a medida que se aproxima al objetivo muestra que la velocidad de la bala de cañón se está acelerando como se ve en la plataforma giratoria, debido a las fuerzas ficticias de Coriolis y centrífugas.

Componentes de aceleración en un momento anterior (arriba) y en el momento de llegada al objetivo (abajo)

La aceleración de Coriolis, la aceleración centrífuga y los vectores de aceleración neta en tres puntos seleccionados de la trayectoria como se ve en el plato giratorio.

La animación en la parte superior de este artículo es una ilustración clásica de la fuerza de Coriolis. Otra visualización de Coriolis y fuerzas centrífugas es este clip de animación.

Dado el radio R del plato giratorio en esa animación, la velocidad de rotación angular ω y la velocidad de la bala de cañón (supuesta constante) v , el ángulo correcto θ para apuntar y golpear el objetivo en el borde del plato giratorio puede ser calculado.

El marco de referencia inercial proporciona una manera de manejar la pregunta: calcular el tiempo de intercepción, que es t _f = R / v . Luego, el plato giratorio gira en un ángulo ω t _fen este tiempo. Si el cañón tiene un ángulo apuntado θ = ω t _f = ω R / v , entonces la bala de cañón llega a la periferia en la posición número 3 al mismo tiempo que el objetivo.

Ninguna discusión sobre la fuerza de Coriolis puede llegar a esta solución de manera tan simple, por lo que la razón para tratar este problema es demostrar el formalismo de Coriolis en una situación fácilmente visualizable.

Trayectoria en el marco inercial [ editar ]

La trayectoria en el marco inercial (denotado A ) es una trayectoria radial de línea recta en el ángulo θ. La posición del cañón en coordenadas ( x , y ) en el tiempo t es:

$${\ displaystyle \ mathbf {r} _ {A} (t) = vt \ \ left (\ cos \ theta, \ \ sin \ theta \ right) \.}

En el marco de la plataforma giratoria (denotado como B ), los ejes x - y giran a una velocidad angular ω, por lo que la trayectoria se convierte en:

$${\ displaystyle \ mathbf {r} _ {B} (t) = vt \ \ left (\ cos (\ theta - \ omega t), \ \ sin (\ theta - \ omega t) \ right) \,}

y tres ejemplos de este resultado se representan en la figura.

Aceleraciones [ editar ]

Componentes de la aceleración [ editar ]

Para determinar los componentes de la aceleración, se usa una expresión general del artículo fuerza ficticia :

$${\ displaystyle \ mathbf {a} _ {B} = \ mathbf {a} _ {A} \; - \; 2 {\ boldsymbol {\ Omega}} \ times \ mathbf {v} _ {B} \; \; {\ boldsymbol {\ Omega}} \ times \ left ({\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} \ right) \; - \; {\ frac {d {\ boldsymbol {\ Omega}}} {dt}} \ times \ mathbf {r} _ {B}}

en el que el término en Ω × v _B es la aceleración de Coriolis y el término en Ω × ( Ω × r _B ) es la aceleración centrífuga. Los resultados son (sea α = θ - ω t ):

{\ displaystyle {\ begin {alineado} {\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} & = \; {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol { j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ tv \ cos \ alpha & tv \ sin \ alpha & 0 \ end {vmatrix}} \; = \ omega t \, v \ left (- \ sin \ alpha, \ cos \ alpha \ right) \, \\ {\ boldsymbol {\ Omega}} \ times \ left ({\ boldsymbol {\ Omega}} \ times \ mathbf {r} _ {B} \ right) & = \; {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol {j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ - \ omega tv \ sin \ alpha & \ omega tv \ cos \ alpha & 0 \ end {vmatrix}} \; = \ omega ^ {2} t \, v \ left (- \ cos \ alpha, - \ sin \ alpha \ right), \ end {alineado}}}

Produciendo aceleraciones [ editar ]

Produciendo una aceleración centrífuga:

$${\ displaystyle \ mathbf {a} _ {\ text {Cfgl}} = \ omega ^ {2} vt \ left (\ cos \ alpha, \ \ sin \ alpha \ right) = \ omega ^ {2} \ mathbf { r} _ {B} (t) \.}

También:

{\ displaystyle {\ begin {alineado} \ mathbf {v} _ {B} = {\ frac {d \ mathbf {r} _ {B} (t)} {dt}} & = (v \ cos \ alpha + \ omega tv \ sin \ alpha, \ v \ sin \ alpha - \ omega tv \ cos \ alpha, \ 0) \, \\ {\ boldsymbol {\ Omega}} \ times \ mathbf {v} _ {B} & = {\ begin {vmatrix} {\ boldsymbol {i}} & {\ boldsymbol {j}} & {\ boldsymbol {k}} \\ 0 & 0 & \ omega \\ v \ cos \ alpha + {} & v \ sin \ alpha - {} & \\\ quad \ omega tv \ sin \ alpha & \ quad \ omega tv \ cos \ alpha & 0 \ end {vmatrix}} \, \ end {alineado}}}

produciendo una aceleración de Coriolis:

{\ displaystyle {\ begin {alineado} \ mathbf {a} _ {\ text {Cor}} & = - 2 \ left [- \ omega v \ left (\ sin \ alpha - \ omega t \ cos \ alpha \ right ), \ \ omega v \ left (\ cos \ alpha + \ omega t \ sin \ alpha \ right) \ right] \\ & = 2 \ omega v \ left (\ sin \ alpha, \ - \ cos \ alpha \ derecha) -2 \ omega ^ {2} \ mathbf {r} _ {B} (t) \. \ end {alineado}}}

Estas aceleraciones se muestran en los diagramas para un ejemplo particular.

Se ve que la aceleración de Coriolis no solo cancela la aceleración centrífuga, sino que juntas proporcionan una red "centrípeta", componente radialmente hacia adentro de la aceleración (es decir, dirigida hacia el centro de rotación): ^[33]

$${\ displaystyle \ mathbf {a _ {\ mathrm {Cptl}}} = - \ omega ^ {2} \ mathbf {r_ {B}} (t) \,}

y un componente adicional de la aceleración perpendicular a r _B ( t ):

$${\ displaystyle \ mathbf {a} _ {C \ perp} = 2 \ omega v \ left (\ sin \ alpha, \ - \ cos \ alpha \ right) \.}

El componente "centrípeto" de la aceleración se parece al movimiento circular en el radio r _B , mientras que el componente perpendicular es dependiente de la velocidad, aumenta con la velocidad radial v y se dirige a la derecha de la velocidad. La situación podría describirse como un movimiento circular combinado con una "aceleración aparente de Coriolis" de 2ω v . Sin embargo, este es un etiquetado aproximado: una designación cuidadosa de la verdadera fuerza centrípeta se refiere a un marco de referencia local que emplea las direcciones normal y tangencial a la trayectoria, no las coordenadas referidas al eje de rotación.

Estos resultados también se pueden obtener directamente por dos diferenciaciones de tiempo de r _B ( t ). El acuerdo de los dos enfoques demuestra que uno podría comenzar desde la expresión general para la aceleración ficticia anterior y derivar las trayectorias que se muestran aquí. Sin embargo, trabajar desde la aceleración hasta la trayectoria es más complicado que el procedimiento inverso utilizado aquí, lo cual es posible en este ejemplo al conocer la respuesta de antemano.

Como resultado de este análisis, aparece un punto importante: todas las aceleraciones ficticias deben incluirse para obtener la trayectoria correcta. En particular, además de la aceleración de Coriolis, la fuerza centrífugajuega un papel esencial. Es fácil obtener la impresión de las discusiones verbales sobre el problema de la bala de cañón, que se centran en mostrar el efecto de Coriolis en particular, que la fuerza de Coriolis es el único factor que debe considerarse, ^[34] pero no es así. ^[35] Un plato giratorio para el cual la fuerza de Coriolis es el único factor es el plato giratorio parabólico. Una situación algo más compleja es el ejemplo idealizado de rutas de vuelo en largas distancias, donde la fuerza centrífuga de la trayectoria y la sustentación aeronáutica se contrarrestan por atracción gravitacional . ^[36] [37]

Bola lanzada en un carrusel giratorio [ editar ]

Un carrusel está girando a la izquierda. Panel izquierdo : una bola es lanzada por un lanzador a las 12:00 en punto y viaja en línea recta hacia el centro del carrusel. Mientras viaja, el lanzador gira en sentido contrario a las agujas del reloj. Panel derecho: el movimiento de la bola visto por el lanzador, que ahora permanece a las 12:00 en punto, porque no hay rotación desde su punto de vista.

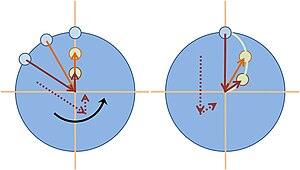
La figura ilustra una bola lanzada desde las 12:00 en punto hacia el centro de un carrusel giratorio a la izquierda. A la izquierda, la pelota es vista por un observador estacionario sobre el carrusel, y la bola viaja en línea recta hacia el centro, mientras que el lanzador de bolas gira en sentido contrario a las agujas del reloj con el carrusel. A la derecha, la pelota es vista por un observador que gira con el carrusel, por lo que el lanzador de pelota parece quedarse a las 12:00 en punto. La figura muestra cómo se puede construir la trayectoria de la bola vista por el observador rotativo.

A la izquierda, dos flechas ubican la bola en relación con el lanzador de bolas. Una de estas flechas es desde el lanzador hasta el centro del carrusel (que proporciona la línea de visión del lanzador de la pelota), y la otra parte desde el centro del carrusel hasta la pelota. (Esta flecha se acorta cuando la bola se acerca al centro.) Una versión desplazada de las dos flechas se muestra punteada.

A la derecha se muestra este mismo par de flechas de puntos, pero ahora el par está girado rígidamente, de modo que la flecha correspondiente a la línea de visión del lanzador de bolas hacia el centro del carrusel está alineada con las 12:00 en punto. La otra flecha del par ubica la bola en relación con el centro del carrusel, proporcionando la posición de la bola como la ve el observador que gira. Al seguir este procedimiento para varias posiciones, la trayectoria en el marco de referencia giratorio se establece como se muestra en la trayectoria curva en el panel de la derecha.

La bola viaja en el aire, y no hay fuerza neta sobre ella. Para el observador estacionario, la pelota sigue una trayectoria en línea recta, por lo que no hay problema al cuadrar esta trayectoria con una fuerza neta cero. Sin embargo, el observador rotativo ve un camino curvo . La cinemática insiste en que debe haber una fuerza (empujando a la derecha de la dirección de desplazamiento instantánea para girar en sentido contrario a las agujas del reloj ) para causar esta curvatura, de modo que el observador giratorio se ve obligado a invocar una combinación de fuerzas centrífugas y de Coriolis para proporcionar la red. Fuerza necesaria para provocar la trayectoria curva.

Pelota que rebota [ editar ]

A vista de pájaro del carrusel. El carrusel gira en sentido horario. Se ilustran dos puntos de vista: el de la cámara en el centro de rotación que gira con el carrusel (panel izquierdo) y el del observador inercial (estacionario) (panel derecho). Ambos observadores acuerdan en un momento dado qué tan lejos está la pelota del centro del carrusel, pero no en su orientación. Los intervalos de tiempo son 1/10 de tiempo desde el lanzamiento hasta el rebote.

La figura describe una situación más compleja en la que la bola lanzada en un plato giratorio rebota en el borde del carrusel y luego regresa a la lanzadora, que atrapa la bola. El efecto de la fuerza de Coriolis en su trayectoria se muestra de nuevo como lo ven dos observadores: un observador (denominado "cámara") que gira con el carrusel y un observador inercial. La figura muestra una vista de pájaro basada en la misma velocidad de la bola en las rutas de avance y retorno. Dentro de cada círculo, los puntos trazados muestran los mismos puntos de tiempo. En el panel izquierdo, desde el punto de vista de la cámara en el centro de rotación, el lanzador (cara sonriente) y el riel se encuentran en ubicaciones fijas, y la bola hace un arco considerable en su viaje hacia el riel, y toma una dirección más directa. Ruta de regreso. Desde el punto de vista del lanzador de bolas,

En el carrusel, en lugar de lanzar la bola directamente a una barandilla para rebotar, el lanzador debe lanzar la bola hacia la derecha del objetivo y la bola luego parece que la cámara debe girar continuamente hacia la izquierda de su dirección de viaje para golpear el riel ( izquierda porque el carrusel gira en sentido horario)). La bola parece inclinarse hacia la izquierda desde la dirección de desplazamiento tanto hacia adentro como hacia atrás en las trayectorias. La trayectoria curva requiere que este observador reconozca una fuerza neta hacia la izquierda en la bola. (Esta fuerza es "ficticia" porque desaparece para un observador estacionario, como se explica brevemente). Para algunos ángulos de lanzamiento, una trayectoria tiene partes donde la trayectoria es aproximadamente radial, y la fuerza de Coriolis es la principal responsable de la aparente desviación del bola (la fuerza centrífuga es radial desde el centro de rotación y causa poca desviación en estos segmentos). Sin embargo, cuando una trayectoria se aleja del radial, la fuerza centrífuga contribuye significativamente a la deflexión.

La trayectoria de la bola a través del aire es recta cuando la observan observadores que se encuentran en el suelo (panel derecho). En el panel de la derecha (observador estacionario), el lanzador de bolas (cara sonriente) está a las 12 en punto y el riel desde el que rebota la bola está en la posición uno (1). Desde el punto de vista del espectador inercial, las posiciones uno (1), dos (2), tres (3) están ocupadas en secuencia. En la posición 2, la pelota golpea el riel y en la posición 3 la pelota regresa al tirador. Se siguen caminos en línea recta porque la bola está en vuelo libre, por lo que este observador requiere que no se aplique fuerza neta.

Aplicado a la tierra [ editar ]

El concepto "fuerza de Coriolis" es especialmente adecuado para la descripción del movimiento de la atmósfera (es decir, los vientos) sobre la superficie de la Tierra. La Tierra (como todos los cuerpos celestes giratorios) ha tomado una forma oblata tal que la fuerza gravitacional está ligeramente desplazada hacia el eje de la Tierra como se ilustra en la figura.

Equilibrio entre la fuerza centrífuga y gravitacional sobre la superficie de la Tierra.

Para un punto de masa en reposo en la superficie de la Tierra, el componente horizontal de la gravitación contrarresta la "fuerza centrífuga" que evita que se deslice hacia el ecuador. Esto significa que el término vectorial de la "ecuación de movimiento" anterior

$${\ displaystyle \ omega ^ {2} {\ boldsymbol {r}} _ {ort} \ + {\ boldsymbol {f}}}

Se dirige directamente hacia abajo, ortogonal a la superficie de la Tierra. La fuerza que afecta el movimiento del aire "deslizante" sobre la superficie de la Tierra es, por lo tanto, (solo) el componente horizontal del término Coriolis

$${\ displaystyle -2 \, {\ boldsymbol {\ Omega \ times v}}}

Este componente es ortogonal a la velocidad sobre la superficie de la Tierra y está dado por la expresión

$${\ displaystyle \ omega \, v \ 2 \, \ sin \ phi}

dónde

$${\ displaystyle \ omega} es la velocidad de giro de la Tierra

$${\ displaystyle \ phi} es la latitud, positiva en el hemisferio norte y negativa en el hemisferio sur

En el hemisferio norte, donde el signo es positivo, esta fuerza / aceleración está a la derecha de la dirección de movimiento, en el hemisferio sur, donde el signo es negativo, esta fuerza / aceleración está a la izquierda de la dirección de movimiento

Explicación intuitiva [ editar ]

A medida que la Tierra gira alrededor de su eje, todo lo que está unido a ella, incluida la atmósfera, gira con ella (imperceptiblemente a nuestros sentidos). Un objeto que se mueve sin ser arrastrado junto con la rotación de la superficie o la atmósfera, como un objeto en vuelo balístico o una masa de aire independiente dentro de la atmósfera, se desplaza en línea recta sobre el giro de la Tierra. Desde nuestra perspectiva de rotación en el planeta, la dirección del movimiento de un objeto en vuelo balístico cambia a medida que se mueve, inclinándose en la dirección opuesta a nuestro movimiento real. Cuando se ve desde un punto estacionario en el espacio directamente sobre el polo norte, cualquier característica de la tierra en el hemisferio norte gira en sentido contrario a las agujas del reloj y, al fijarnos en esa ubicación, cualquier otra ubicación en ese hemisferio gira alrededor de él de la misma manera. El camino de tierra trazado de un cuerpo que se mueve libremente en un vuelo balístico que viaja de un punto a otro, por lo tanto se dobla en sentido contrario a las manecillas del reloj, lo que se denomina convencionalmente "correcto", donde estará si la dirección del movimiento se considera "adelante" y "abajo" Se define naturalmente.

Esfera giratoria [ editar ]

Sistema de coordenadas en la latitud φ con el eje x al este, el eje y alnorte y el eje z hacia arriba (es decir, radialmente hacia afuera desde el centro de la esfera).

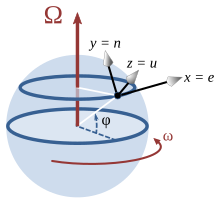
Considere una ubicación con la latitud φ en una esfera que está girando alrededor del eje norte-sur. ^[38] Un sistema de coordenadas local se configura con el eje x horizontalmente hacia el este, el eje yhorizontalmente hacia el norte y el eje z verticalmente hacia arriba. El vector de rotación, la velocidad de movimiento y la aceleración de Coriolis expresada en este sistema de coordenadas local (enumerando los componentes en el orden este ( e ), norte ( n ) y ascendente ( u )) son:

$${\ displaystyle {\ boldsymbol {\ Omega}} = \ omega {\ begin {pmatrix} 0 \\ cos \ varphi \\\ sin \ varphi \ end {pmatrix}} \,}     $${\ displaystyle {\ boldsymbol {v}} = {\ begin {pmatrix} v_ {e} \\ v_ {n} \\ v_ {u} \ end {pmatrix}} \,}

$${\ displaystyle {\ boldsymbol {a}} _ {C} = - 2 {\ boldsymbol {\ Omega \ times v}} = 2 \, \ omega \, {\ begin {pmatrix} v_ {n} \ sin \ varphi -v_ {u} \ cos \ varphi \\ - v_ {e} \ sin \ varphi \\ v_ {e} \ cos \ varphi \ end {pmatrix}} \.}

Al considerar la dinámica atmosférica u oceánica, la velocidad vertical es pequeña, y el componente vertical de la aceleración de Coriolis es pequeño en comparación con la gravedad. Para tales casos, solo importan los componentes horizontales (este y norte). La restricción de lo anterior al plano horizontal es (configuración v _u  = 0):

$${\ displaystyle {\ boldsymbol {v}} = {\ begin {pmatrix} v_ {e} \\ v_ {n} \ end {pmatrix}} \,}     $${\ displaystyle {\ boldsymbol {a}} _ {c} = {\ begin {pmatrix} v_ {n} \\ - v_ {e} \ end {pmatrix}} \ f \,

dónde $${\ displaystyle f = 2 \ omega \ sin \ varphi \,} Se llama el parámetro de Coriolis.

Al establecer v _n = 0, se puede ver inmediatamente que (para φ y ω positivos) un movimiento que se debe al este produce una aceleración hacia el sur. De manera similar, al configurar v _e = 0, se ve que un movimiento hacia el norte resulta en una aceleración hacia el este. En general, observada horizontalmente, mirando a lo largo de la dirección del movimiento que causa la aceleración, la aceleración siempre se gira 90 ° hacia la derecha y del mismo tamaño, independientemente de la orientación horizontal.

Como un caso diferente, considere la configuración de movimiento ecuatorial φ = 0 °. En este caso, Ω es paralelo al norte o eje n , y:

$${\ displaystyle {\ boldsymbol {\ Omega}} = \ omega {\ begin {pmatrix} 0 \\ 1 \\ 0 \ end {pmatrix}} \,}     $${\ displaystyle {\ boldsymbol {v}} = {\ begin {pmatrix} v_ {e} \\ v_ {n} \\ v_ {u} \ end {pmatrix}} \,}  $${\ displaystyle {\ boldsymbol {a}} _ {C} = - 2 {\ boldsymbol {\ Omega \ times v}} = 2 \, \ omega \, {\ begin {pmatrix} -v_ {u} \\ 0 \\ v_ {e} \ end {pmatrix}} \.}

En consecuencia, un movimiento hacia el este (es decir, en la misma dirección que la rotación de la esfera) proporciona una aceleración hacia arriba conocida como el efecto Eötvös , y un movimiento hacia arriba produce una aceleración hacia el oeste.

Para ver ejemplos adicionales en este artículo, vea el cañón en la plataforma giratoria y la bola lanzada . En otros artículos, vea esferas giratorias , movimiento aparente de objetos estacionarios y carrusel .

Meteorología [ editar ]

Este sistema de baja presión sobre Islandia gira en contra de las manecillas del reloj debido al equilibrio entre la fuerza de Coriolis y la fuerza del gradiente de presión.

Representación esquemática del flujo alrededor de un área de bajapresión en el hemisferio norte. El número de Rossby es bajo, por lo que la fuerza centrífuga es prácticamente despreciable. La fuerza del gradiente de presión está representada por flechas azules, la aceleración de Coriolis (siempre perpendicular a la velocidad) por flechas rojas

Representación esquemática de círculos de inercia de masas de aire en ausencia de otras fuerzas, calculadas para una velocidad del viento de aproximadamente 50 a 70 m / s (110 a 160 mph).

Formaciones de nubes en una famosa imagen de la Tierra del Apolo 17, hace que una circulación similar sea directamente visible

Quizás el impacto más importante del efecto Coriolis sea en la dinámica a gran escala de los océanos y la atmósfera. En meteorología y oceanografía , es conveniente postular un marco de referencia giratorio en el que la Tierra está estacionaria. En la acomodación de esa postulación provisional, se introducen las fuerzas centrífugas y de Coriolis. Su importancia relativa está determinada por los números de Rossby aplicables . Los tornados tienen altos números de Rossby, por lo tanto, mientras que las fuerzas centrífugas asociadas a los tornados son bastante importantes, las fuerzas de Coriolis asociadas con los tornados son insignificantes para fines prácticos. ^[39]

Debido a que las corrientes oceánicas superficiales son impulsadas por el movimiento del viento sobre la superficie del agua, la fuerza de Coriolis también afecta el movimiento de las corrientes oceánicas y los ciclones . Muchas de las corrientes más grandes del océano circulan alrededor de áreas cálidas y de alta presión llamadas giros . Aunque la circulación no es tan significativa como la del aire, la desviación causada por el efecto Coriolis es lo que crea el patrón en espiral en estos giros. El patrón de viento en espiral ayuda a la forma de huracán. Cuanto más fuerte es la fuerza del efecto Coriolis, más rápido gira el viento y recoge energía adicional, lo que aumenta la fuerza del huracán. ^[40]

El aire dentro de los sistemas de alta presión gira en una dirección tal que la fuerza de Coriolis se dirige radialmente hacia adentro, y casi se equilibra por el gradiente de presión radial hacia el exterior. Como resultado, el aire viaja en el sentido de las agujas del reloj alrededor de la alta presión en el hemisferio norte y en el sentido contrario a las agujas del reloj en el hemisferio sur. El aire alrededor de baja presión gira en la dirección opuesta, de modo que la fuerza de Coriolis se dirige radialmente hacia afuera y casi equilibra un gradiente de presión radial hacia adentro . ^{[41] [ cita requerida ]}

Flujo alrededor de un área de baja presión [ editar ]

Artículo principal: Área de baja presión.

Si se forma un área de baja presión en la atmósfera, el aire tiende a fluir hacia ella, pero se desvía perpendicular a su velocidad por la fuerza de Coriolis. Un sistema de equilibrio puede entonces establecerse creando un movimiento circular, o un flujo ciclónico. Debido a que el número de Rossby es bajo, el balance de fuerza es mayormente entre la fuerza del gradiente de presión que actúa hacia el área de baja presión y la fuerza de Coriolis que actúa lejos del centro de la presión baja.

En lugar de fluir por el gradiente, los movimientos a gran escala en la atmósfera y el océano tienden a ocurrir perpendicular al gradiente de presión. Esto se conoce como flujo geostrófico . ^[42] En un planeta no giratorio, el fluido fluiría a lo largo de la línea más recta posible, eliminando rápidamente los gradientes de presión. Tenga en cuenta que el equilibrio geostrófico es, por lo tanto, muy diferente del caso de los "movimientos inerciales" (ver más abajo), lo que explica por qué los ciclones de latitud media son más grandes en un orden de magnitud que el flujo del círculo inercial.

Este patrón de desviación, y la dirección del movimiento, se llama ley de Buys-Ballot . En la atmósfera, el patrón de flujo se llama ciclón . En el hemisferio norte, la dirección del movimiento alrededor de un área de baja presión es en sentido contrario a las agujas del reloj. En el hemisferio sur, la dirección del movimiento es en el sentido de las agujas del reloj porque la dinámica de rotación es una imagen de espejo allí. ^[43]En altitudes elevadas, el aire que se extiende hacia afuera gira en la dirección opuesta. ^{[44] Los} ciclones rara vez se forman a lo largo del ecuador debido al débil efecto Coriolis presente en esta región. ^[45]

Círculos de inercia [ editar ]

Una masa de aire o agua en movimiento con velocidad. $${\ displaystyle v \,}sujeto solo a la fuerza de Coriolis, viaja en una trayectoria circular llamada "círculo de inercia". Dado que la fuerza se dirige en ángulo recto al movimiento de la partícula, se mueve con una velocidad constante alrededor de un círculo cuyo radio$${\ displaystyle R} es dado por:

$${\ displaystyle R = {\ frac {v} {f}} \,}

dónde $${\ displaystyle f} es el parámetro de Coriolis $${\ displaystyle 2 \ Omega \ sin \ varphi}, introducido anteriormente (donde $${\ displaystyle \ varphi}es la latitud). Por lo tanto, el tiempo que tarda la masa en completar un círculo completo es$${\ displaystyle 2 \ pi / f}. El parámetro Coriolis generalmente tiene un valor de latitud media de aproximadamente 10 ⁻⁴ s ⁻¹ ; por lo tanto, para una velocidad atmosférica típica de 10 m / s (22 mph), el radio es de 100 km (62 mi), con un período de aproximadamente 17 horas. Para una corriente oceánica con una velocidad típica de 10 cm / s (0.22 mph), el radio de un círculo inercial es de 1 km (0.6 mi). Estos círculos inerciales son en el sentido de las agujas del reloj en el hemisferio norte (donde las trayectorias se doblan hacia la derecha) y en el sentido contrario a las agujas del reloj en el hemisferio sur.

Si el sistema giratorio es un plato giratorio parabólico, entonces $${\ displaystyle f}Es constante y las trayectorias son círculos exactos. En un planeta en rotación,$${\ displaystyle f}Varía con la latitud y los caminos de las partículas no forman círculos exactos. Ya que el parametro$${\ displaystyle f}varía según el seno de la latitud, el radio de las oscilaciones asociadas con una velocidad dada son más pequeños en los polos (latitud = ± 90 °), y aumentan hacia el ecuador. ^[46]

Otros efectos terrestres [ editar ]

El efecto Coriolis afecta fuertemente a la circulación oceánica y atmosférica a gran escala , lo que lleva a la formación de características robustas como corrientes en chorro y corrientes fronterizas occidentales . Dichas características se encuentran en equilibrio geostrófico , lo que significa que el Coriolis y las fuerzas de gradiente de presión se equilibran entre sí. La aceleración de Coriolis también es responsable de la propagación de muchos tipos de ondas en el océano y la atmósfera, incluidas las ondas de Rossby y las ondas de Kelvin . También es fundamental en las llamadas dinámicas de Ekman en el océano y en el establecimiento del patrón de flujo oceánico a gran escala denominado balance de Sverdrup..

Efecto Eötvös [ editar ]

Artículo principal: Efecto Eötvös.

El impacto práctico del "efecto Coriolis" está causado principalmente por el componente de aceleración horizontal producido por el movimiento horizontal.

Hay otros componentes del efecto Coriolis. Los objetos que viajan hacia el oeste se desvían hacia abajo (se sienten más pesados), mientras que los objetos que viajan hacia el este se desvían hacia arriba (se sienten más livianos). ^[47] Esto se conoce como el efecto Eötvös . Este aspecto del efecto Coriolis es mayor cerca del ecuador. La fuerza producida por este efecto es similar a la componente horizontal, pero las fuerzas verticales mucho más grandes debido a la gravedad y la presión significan que generalmente no es importante dinámicamente.

Además, los objetos que viajan hacia arriba ( es decir , hacia afuera) o hacia abajo ( es decir , hacia adentro) se desvían hacia el oeste o el este respectivamente. Este efecto es también el más grande cerca del ecuador. Como el movimiento vertical suele ser de una extensión y duración limitadas, el tamaño del efecto es más pequeño y requiere instrumentos precisos para su detección. Sin embargo, en el caso de grandes cambios de momento, como el lanzamiento de una nave espacial en órbita, el efecto se vuelve significativo. La ruta a la órbita más rápida y con mayor eficiencia de combustible es un lanzamiento desde el ecuador que se curva hacia un rumbo directamente hacia el este.

Ejemplo intuitivo [ editar ]

Imagine un tren que viaja a través de una línea de ferrocarril sin fricción a lo largo del ecuador . Suponga que, cuando está en movimiento, se mueve a la velocidad necesaria para completar un viaje alrededor del mundo en un día (465 m / s). ^[48] El efecto Coriolis puede considerarse en tres casos: cuando el tren viaja hacia el oeste, cuando está en reposo y cuando viaja hacia el este. En cada caso, el efecto de Coriolis se puede calcular a partir del marco de referencia giratorio en la Tierra primero, y luego se debe comparar con un marco de inercia fijo . La imagen de abajo ilustra los tres casos vistos por un observador en reposo en un marco inercial (cercano) desde un punto fijo sobre el Polo Norte a lo largo del eje de rotación de la Tierra.; Los trenes son unos pocos píxeles rojos, fijados en el lado izquierdo en la imagen de la izquierda, moviéndose en los otros.$${\ displaystyle (1 {\ text {day}} \; {\ overset {\ land} {=}} \; 8 {\ text {s}}):}

1. El tren viaja hacia el oeste: en ese caso, se mueve en contra de la dirección de rotación. Por lo tanto, en el marco giratorio de la Tierra, el término Coriolis se señala hacia el eje de rotación (hacia abajo). Esta fuerza adicional hacia abajo debería hacer que el tren sea más pesado mientras se mueve en esa dirección.

• Si uno mira este tren desde el marco fijo no giratorio en la parte superior del centro de la Tierra, a esa velocidad permanece estacionario mientras la Tierra gira debajo de él. Por lo tanto, la única fuerza que actúa sobre él es la gravedad y la reacción de la pista. Esta fuerza es mayor (en un 0,34%) ^[48] que la fuerza que experimentan los pasajeros y el tren cuando están en reposo (girando junto con la Tierra). Esta diferencia es lo que explica el efecto Coriolis en el marco de referencia giratorio.

2. El tren se detiene: desde el punto de vista del marco giratorio de la Tierra, la velocidad del tren es cero, por lo que la fuerza de Coriolis también es cero y el tren y sus pasajeros recuperan su peso habitual.

• Desde el marco de referencia inercial fijo sobre la Tierra, el tren ahora gira junto con el resto de la Tierra. El 0.34% de la fuerza de gravedad proporciona la fuerza centrípeta necesaria para lograr el movimiento circular en ese marco de referencia. La fuerza restante, medida por una escala, hace que el tren y los pasajeros sean "más ligeros" que en el caso anterior.

3. El tren viaja al este. En este caso, debido a que se mueve en la dirección del marco giratorio de la Tierra, el término Coriolis se dirige hacia afuera desde el eje de rotación (arriba). Esta fuerza hacia arriba hace que el tren parezca más liviano que en reposo.

Gráfico de la fuerza experimentada por un objeto de 10 kilogramos en función de su velocidad que se mueve a lo largo del ecuador de la Tierra (medida dentro del marco giratorio). (La fuerza positiva en el gráfico se dirige hacia arriba. La velocidad positiva se dirige hacia el este y la velocidad negativa hacia el oeste).

• Desde el marco de referencia inercial fijo por encima de la Tierra, el tren que viaja hacia el este ahora gira al doble de la velocidad que cuando estaba en reposo, por lo que la cantidad de fuerza centrípeta necesaria para hacer que la trayectoria circular aumente deje que la fuerza de la gravedad actúe sobre la vía. . Esto es lo que el término Coriolis explica en el párrafo anterior.
• Como comprobación final se puede imaginar un marco de referencia que gira junto con el tren. Dicho marco giraría al doble de la velocidad angular que el marco giratorio de la Tierra. El componente resultante de la fuerza centrífuga para ese marco imaginario sería mayor. Dado que el tren y sus pasajeros están en reposo, ese sería el único componente en ese marco que explicaría de nuevo por qué el tren y los pasajeros son más livianos que en los dos casos anteriores.

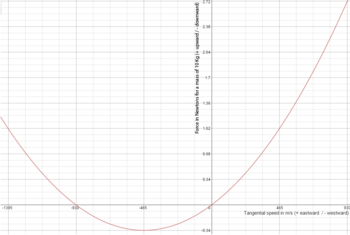
Esto también explica por qué los proyectiles de alta velocidad que viajan hacia el oeste se desvían hacia abajo, y los que viajan hacia el este se desvían hacia arriba. Esta componente vertical del efecto Coriolis se denomina efecto Eötvös . ^[49]

El ejemplo anterior se puede usar para explicar por qué el efecto Eötvös comienza a disminuir cuando un objeto viaja hacia el oeste a medida que su velocidad tangencialaumenta por encima de la rotación de la Tierra (465 m / s). Si el tren hacia el oeste en el ejemplo anterior aumenta la velocidad, parte de la fuerza de gravedad que empuja contra la vía da cuenta de la fuerza centrípeta necesaria para mantenerlo en movimiento circular en el marco inercial. Una vez que el tren duplica su velocidad hacia el oeste a 930 m / s, la fuerza centrípeta se iguala a la fuerza que experimenta el tren cuando se detiene. Desde el marco inercial, en ambos casos, gira a la misma velocidad pero en direcciones opuestas. Así, la fuerza es la misma cancelando completamente el efecto Eötvös. Cualquier objeto que se mueve hacia el oeste a una velocidad superior a 930 m / s experimenta una fuerza ascendente en su lugar. En la figura, el efecto Eötvös se ilustra para un objeto de 10 kilogramos en el tren a diferentes velocidades. La forma parabólica se debe a la fuerza centrípeta.Es proporcional al cuadrado de la velocidad tangencial. En el marco inercial, la parte inferior de la parábola está centrada en el origen. El desplazamiento se debe a que este argumento utiliza el marco de referencia giratorio de la Tierra. La gráfica muestra que el efecto Eötvös no es simétrico, y que la fuerza descendente resultante experimentada por un objeto que viaja hacia el oeste a alta velocidad es menor que la fuerza ascendente resultante cuando viaja hacia el este a la misma velocidad.

Drenaje en bañeras e inodoros [ editar ]

Contrariamente a la idea errónea popular, la rotación del agua en los baños domésticos en circunstancias normales no está relacionada con el efecto Coriolis ni con la rotación de la Tierra, y no se puede observar una diferencia constante en la dirección de rotación entre el drenaje del inodoro en los hemisferios norte y sur. ^{[50] [51] [52] [53]} La formación de un vórtice sobre el orificio del tapón puede explicarse por la conservación del momento angular : el radio de rotación disminuye a medida que el agua se acerca al orificio del tapón, por lo que aumenta la velocidad de rotación, por la misma razón que la velocidad de giro de un patinador sobre hielo aumenta al jalar sus brazos hacia adentro. Cualquier rotación alrededor del orificio del tapón que inicialmente está presente se acelera a medida que el agua se mueve hacia adentro.

La fuerza de Coriolis todavía afecta la dirección del flujo de agua, pero solo de forma minuciosa. Solo si el agua está tan quieta que la velocidad de rotación efectiva de la Tierra es más rápida que la del agua en relación con su contenedor, y si los pares aplicados externamente (como los que pueden ser causados ​​por el flujo sobre una superficie inferior desigual) son lo suficientemente pequeños. el efecto Coriolis puede determinar la dirección del vórtice. Sin una preparación tan cuidadosa, es probable que el efecto Coriolis sea mucho más pequeño que otras influencias en la dirección del drenaje ^[54] , como cualquier rotación residual del agua ^[55] y la geometría del recipiente. ^[56]A pesar de esto, la idea de que los inodoros y las bañeras drenan de manera diferente en los hemisferios norte y sur ha sido popularizada por varios programas de televisión y películas, como Escape Plan , Wedding Crashers , el episodio " Bart vs. Australia " de The Simpsons , Pole to Pole , ^{[57 ] [58]} y el episodio de The X-Files " Die Hand Die Verletzt ". ^[59] Varias emisiones y publicaciones científicas, incluido al menos un libro de texto de física a nivel universitario, también lo han declarado. ^[60] [61]

En 1908, el físico austriaco Ottokar Tumlirz describió experimentos cuidadosos y efectivos que demostraron el efecto de la rotación de la Tierra en la salida de agua a través de una abertura central. ^[62] El tema fue posteriormente popularizado en un famoso artículo de 1962 en la revista Nature., que describió un experimento en el que se eliminaron todas las demás fuerzas del sistema al llenar un tanque de 6 pies (1,8 m) con 300 galones de EE. UU. (1,100 L) de agua y permitir que se asiente durante 24 horas (para permitir cualquier movimiento debido a llenando el tanque para morir), en una habitación donde la temperatura se había estabilizado. Luego se retiró el tapón de drenaje muy lentamente y se usaron pequeñas piezas de madera flotante para observar la rotación. Durante los primeros 12 a 15 minutos, no se observó rotación. Luego, apareció un vórtice y comenzó a girar constantemente en sentido contrario a las agujas del reloj (el experimento se realizó en Boston, Massachusetts)., en el hemisferio norte). Esto se repitió y los resultados se promediaron para asegurar que el efecto fuera real. El informe señaló que el vórtice giró, "unas 30,000 veces más rápido que la rotación efectiva de la Tierra en 42 ° Norte (la ubicación del experimento)". Esto muestra que la pequeña rotación inicial debida a la Tierra se amplifica por el drenaje gravitacional y la conservación del momento angular para convertirse en un vórtice rápido y se puede observar en condiciones de laboratorio cuidadosamente controladas . ^[63] [64]

Trayectorias balísticas [ editar ]

La fuerza de Coriolis es importante en balística externa para calcular las trayectorias de los proyectiles de artillería de muy largo alcance . El ejemplo histórico más famoso fue el cañón de París , utilizado por los alemanes durante la Primera Guerra Mundial para bombardear París desde un rango de alrededor de 120 km (75 mi). La fuerza de Coriolis cambia minuciosamente la trayectoria de una bala, afectando la precisión a distancias extremadamente largas. Se ajusta mediante tiradores precisos de larga distancia, como francotiradores. En la latitud de Sacramentoun tiro de 1000 yardas se desviaría 3 pulgadas a la derecha. También hay un componente vertical, que se explica en la sección de efectos de Eötvös más arriba, que hace que los disparos hacia el oeste alcancen los golpes bajos y que los disparos hacia el este alcancen los niveles altos. ^[28] [65]

Los efectos de la fuerza de Coriolis en las trayectorias balísticas no deben confundirse con la curvatura de las trayectorias de misiles, satélites y objetos similares cuando las trayectorias se trazan en mapas bidimensionales (planos), como la proyección de Mercator . Las proyecciones de la superficie curva tridimensional de la Tierra a una superficie bidimensional (el mapa) necesariamente dan como resultado características distorsionadas. La curvatura aparente del camino es una consecuencia de la esfericidad de la Tierra y se produciría incluso en un marco no giratorio. ^{[ cita requerida ]}

La visualización del efecto Coriolis [ editar ]

Fluido asumiendo una forma parabólica a medida que gira.

El objeto se mueve sin fricción sobre la superficie de un plato parabólico muy superficial. El objeto ha sido lanzado de tal manera que sigue una trayectoria elíptica. 
Izquierda : El punto de vista inercial. 
Derecha : El punto de vista de co-rotación.

Las fuerzas en juego en el caso de una superficie curva. 
Rojo : gravedad 
Verde : la fuerza normal 
Azul : la fuerza centrípeta resultante neta .

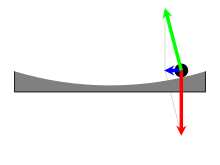
Para demostrar el efecto de Coriolis, se puede utilizar un plato giratorio parabólico. En una mesa giratoria plana, la inercia de un objeto de rotación conjunta lo fuerza fuera del borde. Sin embargo, si la superficie del plato giratorio tiene la forma parabólica (tazón parabólica) correcta (vea la figura) y gira a la velocidad correspondiente, los componentes de fuerza mostrados en la figura hacen que el componente de la gravedad tangencial a la superficie del tazón sea exactamente igual a la fuerza centrípeta necesario para mantener el objeto girando a su velocidad y radio de curvatura (suponiendo que no hay fricción). (Ver giro en banco ). Esta superficie cuidadosamente contorneada permite que la fuerza de Coriolis se muestre de forma aislada. ^[66] [67]

Discos cortados de cilindros de hielo seco.Se puede usar como discos, moviéndose casi sin fricción sobre la superficie de la mesa giratoria parabólica, permitiendo que los efectos de Coriolis en los fenómenos dinámicos se muestren. Para obtener una vista de los movimientos tal como se ven en el marco de referencia que gira con la plataforma giratoria, una videocámara está conectada a la mesa giratoria para girar conjuntamente con la plataforma giratoria, con los resultados que se muestran en la figura. En el panel izquierdo de la figura, que es el punto de vista de un observador estacionario, la fuerza gravitacional en el marco inercial que tira del objeto hacia el centro (parte inferior) del plato es proporcional a la distancia del objeto desde el centro. Una fuerza centrípeta de esta forma provoca el movimiento elíptico. En el panel derecho, que muestra el punto de vista del marco giratorio, la fuerza gravitatoria hacia adentro en el marco giratorio (la misma fuerza que en el marco inercial) es balanceada por la fuerza centrífuga hacia afuera (presente solo en el marco giratorio). Con estas dos fuerzas equilibradas, en el marco giratorio la única fuerza desequilibrada es Coriolis (también presente solo en el marco giratorio), y el movimiento es uncirculo inercial . El análisis y la observación del movimiento circular en el marco giratorio es una simplificación en comparación con el análisis u observación del movimiento elíptico en el marco inercial.

Debido a que este marco de referencia gira varias veces por minuto en lugar de solo una vez al día como la Tierra, la aceleración de Coriolis producida es muchas veces más grande y, por lo tanto, más fácil de observar en escalas espaciales y temporales menores que la aceleración de Coriolis causada por la rotación de la Tierra. .

Como una manera de hablar, la Tierra es análoga a un tocadiscos de este tipo. ^[68] La rotación ha provocado que el planeta se asiente en una forma esferoidal, de modo que la fuerza normal, la fuerza gravitatoria y la fuerza centrífuga se equilibren entre sí exactamente en una superficie "horizontal". (Ver abultamiento ecuatorial .)

El efecto de Coriolis causado por la rotación de la Tierra se puede ver indirectamente a través del movimiento de un péndulo de Foucault .

Efectos de Coriolis en otras áreas [ editar ]

Medidor de flujo de Coriolis [ editar ]

Una aplicación práctica del efecto Coriolis es el medidor de flujo másico , un instrumento que mide el caudal másico y la densidad de un fluido que fluye a través de un tubo. El principio de funcionamiento consiste en inducir una vibración del tubo a través del cual pasa el fluido. La vibración, aunque no es completamente circular, proporciona el marco de referencia giratorio que da lugar al efecto Coriolis. Si bien los métodos específicos varían de acuerdo con el diseño del medidor de flujo, los sensores monitorean y analizan los cambios en la frecuencia, el cambio de fase y la amplitud de los tubos de flujo de vibración. Los cambios observados representan el caudal másico y la densidad del fluido. ^[69]

Física molecular [ editar ]

En las moléculas poliatómicas, el movimiento de la molécula se puede describir mediante una rotación rígida del cuerpo y una vibración interna de los átomos sobre su posición de equilibrio. Como resultado de las vibraciones de los átomos, los átomos están en movimiento en relación con el sistema de coordenadas de rotación de la molécula. Por lo tanto, los efectos de Coriolis están presentes y hacen que los átomos se muevan en una dirección perpendicular a las oscilaciones originales. Esto conduce a una mezcla en los espectros moleculares entre los niveles de rotación y vibración , a partir de los cuales se pueden determinar las constantes de acoplamiento de Coriolis. ^[70]

Precesión giroscópica [ editar ]

Cuando se aplica un par de torsión externo a un giroscopio giratorio a lo largo de un eje que está en ángulo recto con el eje de giro, la velocidad de la llanta que está asociada con el giro se dirige radialmente en relación con el eje de torque externo. Esto hace que una fuerza de Coriolis actúe sobre el borde de tal manera que incline el giroscopio en ángulos rectos en la dirección en que el torque externo lo hubiera inclinado. Esta tendencia tiene el efecto de mantener los cuerpos giratorios alineados de forma estable en el espacio.

Vuelo de insectos [ editar ]

Las moscas ( Diptera ) y algunas polillas ( Lepidoptera ) explotan el efecto Coriolis en vuelo con apéndices y órganos especializados que transmiten información sobre la velocidad angular de sus cuerpos.

Las fuerzas de Coriolis resultantes del movimiento lineal de estos apéndices se detectan dentro del marco giratorio de referencia de los cuerpos de los insectos. En el caso de las moscas, sus apéndices especializados son órganos con forma de mancuernas ubicados justo detrás de sus alas llamadas " cabestros ". ^[71]

Los halterios de la mosca oscilan en un plano a la misma frecuencia de batido que las alas principales, de modo que cualquier rotación del cuerpo produce una desviación lateral de los halteres respecto de su plano de movimiento. ^[72]

En las polillas, se sabe que sus antenas son responsables de la detección de las fuerzas de Coriolis de la misma manera que con los halteres en las moscas. ^[73] Tanto en las moscas como en las polillas, una colección de mecanosensores en la base del apéndice son sensibles a las desviaciones en la frecuencia de batido, correlacionadas con la rotación en los planos de cabeceo y balanceo , y al doble de la frecuencia de batido, correlacionadas con la rotación en el plano avión de guiñada ^[74] [73]