MECÁNICA CLÁSICA

La dinámica browniana (BD) se puede usar para describir el movimiento de las moléculas, por ejemplo, en simulaciones moleculares o en la realidad. Es una versión simplificada de la dinámica de Langevin y corresponde al límite donde no tiene lugar una aceleración media. Esta aproximación también se puede describir como dinámica de Langevin " sobredimensionada ", o como dinámica de Langevin sin inercia .

En la dinámica de Langevin , la ecuación de movimiento es

$${\ displaystyle M {\ ddot {X}} = - \ nabla U (X) - \ gamma {\ dot {X}} + {\ sqrt {2 \ gamma k_ {B} T}} R (t)}

dónde

• $${\ displaystyle \ gamma}es un coeficiente de fricción ,
• $${\ displaystyle U (X)} es el potencial de interacción de partículas,
• $${\ displaystyle \ nabla} es el operador de gradiente tal que $${\ displaystyle - \ nabla U (X)} Es la fuerza calculada a partir de los potenciales de interacción de partículas.
• El punto es un derivado del tiempo tal que $${\ displaystyle {\ dot {X}}} es la velocidad, y $${\ displaystyle {\ ddot {X}}} es la aceleración
• T es la temperatura
• k _B es la constante de Boltzmann
• $${\ displaystyle R (t)}es un proceso Gaussiano estacionario delta correlacionado con media cero, que satisface

$${\ displaystyle \ left \ langle R (t) \ right \ rangle = 0}

$${\ displaystyle \ left \ langle R (t) R (t ') \ right \ rangle = \ delta (t-t').}

En la dinámica browniana, la $${\ displaystyle M {\ ddot {X}} (t)} el término se descuida, y la suma de estos términos es cero.

$${\ displaystyle 0 = - \ nabla U (X) - \ gamma {\ dot {X}} + {\ sqrt {2 \ gamma k_ {B} T}} R (t)}

Usando la relación de Einstein ,$${\ displaystyle D = k_ {B} T / \ gamma}, a menudo es conveniente escribir la ecuación como,

$${\ displaystyle {\ dot {X}} (t) = - {\ frac {D} {k_ {B} T}} \ nabla U (X) + {\ sqrt {2D}} R (t).}

El argumento del cubo giratorio de Isaac Newton (también conocido como el cubo de Newton ) se diseñó para demostrar que el verdadero movimiento de rotación no se puede definir como la rotación relativa del cuerpo con respecto a los cuerpos circundantes. Es uno de los cinco argumentos de las "propiedades, causas y efectos" de "movimiento verdadero y reposo" que apoyan su argumento de que, en general, el movimiento verdadero y el reposo no pueden definirse como instancias especiales de movimiento o reposo en relación con otros cuerpos. , pero en su lugar solo se puede definir por referencia al espacio absoluto . Alternativamente, estos experimentos proporcionan una definición operativa de lo que significa "Rotación absoluta ", y no pretende abordar la cuestión de" rotación relativa a qué " ^[1] La relatividad general prescinde del espacio absoluto y de la física cuya causa es externa al sistema, con el concepto de geodésicas del espacio-tiempo .

Fondo [ editar ]

Estos argumentos, y una discusión de las distinciones entre tiempo absoluto y relativo, espacio, lugar y movimiento, aparecen en un General Scholium al comienzo de la obra de Newton, Los principios matemáticos de la filosofía natural (1687), que establecieron los cimientos de lo clásico. Mecánica e introdujo su ley de gravitación universal , que produjo la primera explicación dinámica cuantitativamente adecuada del movimiento planetario . ^[3]

A pesar de su aceptación del principio de inercia rectilínea y el reconocimiento de la relatividad cinemática del movimiento aparente (que subyace a si el sistema ptolemaico o copernicano es correcto), los filósofos naturales del siglo XVII continuaron considerando el movimiento verdadero y el descanso como descriptores físicamente separados. de un cuerpo individual. La visión dominante a la que se opuso Newton fue ideada por René Descartes , y fue apoyada (en parte) por Gottfried Leibniz. Sostuvo que el espacio vacío es una imposibilidad metafísica porque el espacio no es otra cosa que la extensión de la materia, o, en otras palabras, que cuando se habla del espacio entre las cosas, se está haciendo referencia a la relación que existe entre esas cosas y no a alguna entidad que se interponga entre ellos. ^[4] [5] concordante con el entendimiento anterior, cualquier afirmación sobre el movimiento de un cuerpo se reduce a una descripción con el tiempo en el que el cuerpo en consideración es en t ₁ que se encuentra en las proximidades de un grupo de órganos de "referencia" y en algún t ₂ se encuentra en la proximidad de algún otro cuerpo o cuerpos "hito". ^[6] [7]

Detección de la rotación: las banderas rojas saltan hacia afuera en los brazos flexibles cuando cualquiera de los objetos realmente gira. A: el objeto central gira. B: El anillo exterior gira, pero en dirección opuesta. C: Ambos giran, pero en direcciones opuestas. D: Ambos están bloqueados entre sí y giran en la misma dirección.

Descartes reconoció que habría una diferencia real, sin embargo, entre una situación en la que un cuerpo con partes móviles y originalmente en reposo con respecto a un anillo circundante se aceleró a una cierta velocidad angular con respecto al anillo, y otra situación en A los anillos circundantes se les dio una aceleración contraria con respecto al objeto central. Con respecto exclusivo al objeto central y al anillo circundante, los movimientos serían indistinguibles entre sí suponiendo que tanto el objeto central como el anillo circundante fueran objetos absolutamente rígidos. Sin embargo, si ni el objeto central ni el anillo circundante eran absolutamente rígidos, entonces las partes de uno o ambos tenderían a volar desde el eje de rotación.

Por razones contingentes relacionadas con la Inquisición , Descartes habló del movimiento como absoluto y relativo. ^{[8] [ no en la cita dada ]} Sin embargo, su posición real era que el movimiento es absoluto. ^[9]

A finales del siglo XIX, la afirmación de que todo movimiento es relativo fue reintroducida, en particular por Ernst Mach (1883). ^[10] [11]

Cuando, en consecuencia, decimos que un cuerpo conserva sin cambios su dirección y velocidad en el espacio , nuestra afirmación no es más ni menos que una referencia abreviada a todo el universo .

-  Ernst Mach; según lo citado por Ciufolini y Wheeler : gravitación e inercia , p. 387

El argumento [ editar ]

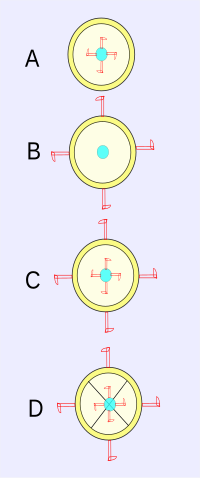
Newton analiza un cubo ( latín : situla ) lleno de agua colgada de un cordón. ^[12] Si el cable se tuerce sobre sí mismo y luego se suelta el cubo, comienza a girar rápidamente, no solo con respecto al experimentador, sino también en relación con el agua que contiene. (Esta situación correspondería al diagrama B anterior.)

Aunque el movimiento relativo en esta etapa es el mayor, la superficie del agua permanece plana, lo que indica que las partes del agua no tienen tendencia a retroceder desde el eje del movimiento relativo, a pesar de la proximidad al cubo. Finalmente, a medida que el cable continúa desenrollando, la superficie del agua toma una forma cóncava a medida que adquiere el movimiento del cucharón girando en relación con el experimentador. Esta forma cóncava muestra que el agua está girando, a pesar del hecho de que el agua está en reposo en relación con el cubo. En otras palabras, no es el movimiento relativo de la cubeta y el agua lo que causa la concavidad del agua, contrariamente a la idea de que los movimientos solo pueden ser relativos y que no hay movimiento absoluto. (Esta situación correspondería al diagrama D). Posiblemente la concavidad del agua muestra una rotación relativa aotra cosa : decir espacio absoluto? Newton dice: "Uno puede descubrir y medir el movimiento circular verdadero y absoluto del agua". ^[13]

En la traducción de 1846 Andrew Motte de las palabras de Newton: ^[14]

Si un barco, colgado por un cable largo, se gira con tanta frecuencia que el cable está fuertemente retorcido, se llena con agua y se mantiene en reposo junto con el agua; después, por la acción repentina de otra fuerza, se gira en sentido contrario, y mientras el cordón se desenrosca, el barco continúa durante algún tiempo este movimiento; la superficie del agua al principio será llana, como antes de que el recipiente comenzara a moverse; pero la vasija comunicando gradualmente su movimiento al agua, hará que comience a girar con sensatez, y retrocederá poco a poco, y ascenderá a los lados de la vasija, formando una figura cóncava ... Este ascenso del agua muestra su empeño por alejarse del eje de su movimiento; y el movimiento circular verdadero y absoluto del agua, que aquí es directamente contrario al familiar, se descubre a sí mismo, y puede medirse por este esfuerzo. ... Y, por lo tanto, este esfuerzo no depende de ninguna traducción del agua con respecto a los cuerpos ambientales, ni se puede definir el verdadero movimiento circular mediante dicha traducción. ...; pero los movimientos relativos ... están totalmente desprovistos de cualquier efecto real. ... De hecho, es una cuestión de gran dificultad descubrir y, efectivamente, distinguir, los verdaderos movimientos de los cuerpos particulares de lo aparente; Debido a que las partes de ese espacio inamovible en el que se realizan estos movimientos, de ninguna manera están bajo la observación de nuestros sentidos. De hecho, es una cuestión de gran dificultad descubrir y, efectivamente, distinguir, los verdaderos movimientos de los cuerpos particulares de lo aparente; Debido a que las partes de ese espacio inamovible en el que se realizan estos movimientos, de ninguna manera están bajo la observación de nuestros sentidos. De hecho, es una cuestión de gran dificultad descubrir y, efectivamente, distinguir, los verdaderos movimientos de los cuerpos particulares de lo aparente; Debido a que las partes de ese espacio inamovible en el que se realizan estos movimientos, de ninguna manera están bajo la observación de nuestros sentidos.

-  Isaac Newton; Principia , libro 1: Scholium

El argumento de que el movimiento es absoluto, no relativo, es incompleto, ya que limita a los participantes relevantes al experimento solo a la cubeta y al agua, una limitación que no se ha establecido. De hecho, la concavidad del agua claramente involucra la atracción gravitacional, y por implicación la Tierra también es un participante. Aquí hay una crítica debido a que Mach argumenta que solo se establece el movimiento relativo: ^[15]

El experimento de Newton con el recipiente de agua giratorio simplemente nos informa que la rotación relativa del agua con respecto a los lados del recipiente no produce fuerzas centrífugas perceptibles, sino que tales fuerzas son producidas por sus rotaciones relativas con respecto a la masa de la tierra. y otros cuerpos celestes.

-  Ernst Mach, citado por L. Bouquiaux en Leibniz , p. 104

El grado en que la hipótesis de Mach se integra en la relatividad general se analiza en el artículo Princip de Mach; en general se sostiene que la relatividad general no es enteramente machiana.

Todos los observadores están de acuerdo en que la superficie del agua en rotación es curva. Sin embargo, la explicación de esta curvatura involucra la fuerza centrífuga para todos los observadores, con la excepción de un observador verdaderamente estacionario, que encuentra que la curvatura es consistente con la velocidad de rotación del agua a medida que la observan, sin necesidad de una fuerza centrífuga adicional. Por lo tanto, se puede identificar un marco estacionario, y no es necesario preguntar "¿Estacionario con respecto a qué?":

La pregunta original, "¿en relación con qué marco de referencia tienen las leyes del movimiento?" Se revela que se plantea incorrectamente. Porque las leyes del movimiento determinanesencialmente una clase de marcos de referencia y (en principio) un procedimiento para construirlos. ^[dieciséis]

Newton también propuso un experimento mental complementario con el mismo objetivo de determinar la ocurrencia de la rotación absoluta: el ejemplo de observar dos esferas idénticas en rotación alrededor de su centro de gravedad y unidas por una cuerda. La ocurrencia de tensión en la cuerda es indicativa de rotación absoluta; Ver esferas giratorias .

Análisis detallado [ editar ]

La interfaz de dos líquidos inmiscibles que giran alrededor de un eje vertical es un paraboloide circular de apertura hacia arriba.

El interés histórico del experimento del cubo giratorio es su utilidad para sugerir que se puede detectar la rotación absoluta observando la forma de la superficie del agua. Sin embargo, uno podría cuestionarse cómo la rotación produce este cambio. A continuación se muestran dos enfoques para comprender la concavidad de la superficie del agua en rotación en un cubo.

Diagrama de fuerza para un elemento de superficie de agua en marco de co-rotación. Parte superior : sección radial y punto seleccionado en la superficie del agua; el agua, el marco de co-rotación, y la sección radial comparten una velocidad angular constante de rotación dada por el vector Ω . Abajo : diagrama de fuerzas en el punto seleccionado de la superficie. La pendiente de la superficie se ajusta para hacer que las tres fuerzas se sumen a cero.

Leyes del movimiento de Newton [ editar ]

La forma de la superficie de un líquido en rotación en un cubo se puede determinar utilizando las leyes de Newton para las diversas fuerzas sobre un elemento de la superficie. Por ejemplo, ver Knudsen y Hjorth. ^[17] El análisis comienza con el diagrama de cuerpo libre en el marco de rotación conjunta donde el agua aparece estacionaria. La altura del agua h = h ( r ) es una función de la distancia radial r del eje de rotación Ω , y el objetivo es determinar esta función. Se muestra que un elemento del volumen de agua en la superficie está sujeto a tres fuerzas: la fuerza vertical debida a la gravedad F _g , la fuerza centrífuga horizontal, radialmente hacia afuera F _Cfgl, y la fuerza normal a la superficie del agua F _n debido al resto del agua que rodea el elemento seleccionado de la superficie. Se sabe que la fuerza debida al agua circundante es normal a la superficie del agua porque un líquido en equilibrio no puede soportar tensiones de corte . ^[18]Para citar a Anthony y Brackett: ^[19]

La superficie de un fluido de densidad uniforme ..., si está en reposo, está en todas partes perpendicular a las líneas de fuerza; porque si esto no fuera así, la fuerza en un punto en la superficie podría resolverse en dos componentes, uno perpendicular y otro tangente a la superficie. Pero a partir de la naturaleza de un fluido, la fuerza tangencial establecería un movimiento del fluido, lo cual es contrario a la afirmación de que el fluido está en reposo.

-  William Arnold Anthony y Cyrus Fogg Brackett: Libro de texto elemental de Física , pág. 127

Además, como el elemento agua no se mueve, la suma de las tres fuerzas debe ser cero. Para sumar a cero, la fuerza del agua debe apuntar de manera opuesta a la suma de las fuerzas centrífugas y de gravedad, lo que significa que la superficie del agua debe ajustarse de modo que sus puntos normales en esta dirección. (Un problema muy similar es el diseño de un giro escalonado , donde la pendiente del giro se establece de modo que un automóvil no se deslice fuera de la carretera. La analogía en el caso de la cuchara giratoria es que el elemento de la superficie del agua se "deslizará" hacia arriba o hacia abajo de la superficie, a menos que la normal a la superficie se alinee con el vector resultante formado por la adición del vector F _g + F _Cfgl .)

A medida que r aumenta, la fuerza centrífuga aumenta según la relación (las ecuaciones se escriben por unidad de masa):

$${\ displaystyle F _ {\ mathrm {Cfgl}} = m {\ mathit {\ Omega}} ^ {2} r \,}

donde Ω es la velocidad constante de rotación del agua. La fuerza gravitacional no cambia en

$${\ displaystyle F _ {\ mathrm {g}} = mg \,}

donde g es la aceleración debida a la gravedad . Estas dos fuerzas se suman para hacer una resultante en un ángulo φ desde la vertical dada por

$${\ displaystyle \ tan \ varphi = {\ frac {F _ {\ mathrm {Cfgl}}} {F _ {\ mathrm {g}}}} = {\ frac {{\ mathit {\ Omega}} ^ {2} r } {g}} \,}

que claramente se hace más grande a medida que r aumenta. Para garantizar que este resultado sea normal a la superficie del agua y, por lo tanto, pueda anularse efectivamente por la fuerza del agua debajo, la normal a la superficie debe tener el mismo ángulo, es decir,

$${\ displaystyle \ tan \ varphi = {\ frac {\ mathrm {d} h} {\ mathrm {d} r}} \,}

llevando a la ecuación diferencial ordinaria para la forma de la superficie:

$${\ displaystyle {\ frac {\ mathrm {d} h} {\ mathrm {d} r}} = {\ frac {{\ \ mathit {\ Omega}} ^ {2} r} {g}} \,}

o, integrando:

$${\ displaystyle h (r) = h (0) + {\ frac {1} {2g}} \ left ({\ mathit {\ Omega}} r \ right) ^ {2} \,}

donde h (0) es la altura del agua en r = 0. En palabras, la superficie del agua es parabólica en su dependencia del radio.

Energía potencial [ editar ]

La forma de la superficie del agua se puede encontrar de una manera diferente, muy intuitiva, utilizando la interesante idea de la energía potencial asociada con la fuerza centrífuga en el marco de rotación conjunta. En un marco de referencia que gira uniformemente a una velocidad angular Ω, la fuerza centrífuga ficticia es conservadora y tiene una energía potencial de la forma: ^[20] [21]

$${\ displaystyle {U} _ {\ mathrm {Cfgl}} = - {\ frac {1} {2}} m \ Omega ^ {2} r ^ {2} \,}

donde r es el radio del eje de rotación. Este resultado se puede verificar tomando el gradiente del potencial para obtener la fuerza radialmente hacia afuera:

$${\ displaystyle F _ {\ mathrm {Cfgl}} = - {\ frac {\ partial} {\ partial r}} {U} _ {\ mathrm {Cfgl}}} $${\ displaystyle = m \ Omega ^ {2} r \.}

El significado de la energía potencial es que el movimiento de un cuerpo de prueba de un radio más grande a un radio más pequeño implica hacer un trabajo contra la fuerza centrífuga.

La energía potencial es útil, por ejemplo, para comprender la concavidad de la superficie del agua en un cubo giratorio. Observe que en el equilibrio la superficie adopta una forma tal que un elemento de volumen en cualquier ubicación de su superficie tiene la misma energía potencial que en cualquier otra. Siendo así, ningún elemento de agua en la superficie tiene ningún incentivo para mover la posición, porque todas las posiciones son equivalentes en energía. Es decir, se alcanza el equilibrio. Por otro lado, si las regiones de superficie tuvieran menor energía disponible, el agua que ocupa las ubicaciones de superficie de mayor potencial de energía se movería para ocupar estas posiciones de menor energía, ya que no existe una barrera para el movimiento lateral en un líquido ideal.

Podríamos imaginarnos alterar deliberadamente esta situación de equilibrio alterando de alguna manera momentáneamente la forma de la superficie del agua para hacerla diferente de una superficie de igual energía. Este cambio en la forma no sería estable, y el agua no se mantendría en nuestra forma artificialmente inventada, sino que se involucraría en una exploración transitoria de muchas formas hasta que se introdujeran fuerzas de fricción no ideales al chapotear, ya sea contra los costados del cubo o por el La naturaleza no ideal del líquido mató las oscilaciones y el agua se asentó en una forma de equilibrio.

Para ver el principio de una superficie de igual energía en el trabajo, imagine que aumenta gradualmente la velocidad de rotación del cucharón desde cero. La superficie del agua es plana al principio, y claramente una superficie de igual energía potencial porque todos los puntos de la superficie están a la misma altura en el campo gravitatorio que actúa sobre el agua. Sin embargo, a una pequeña velocidad de rotación angular, un elemento del agua de la superficie puede alcanzar una energía potencial más baja moviéndose hacia afuera bajo la influencia de la fuerza centrífuga. Debido a que el agua es incompresible y debe permanecer dentro de los límites de la cubeta, este movimiento hacia afuera aumenta la profundidad del agua en el radio más grande, aumentando la altura de la superficie en un radio más grande, y bajándola a un radio más pequeño. La superficie del agua se vuelve ligeramente cóncava, con la consecuencia de que la energía potencial del agua en el radio mayor se incrementa por el trabajo realizado contra la gravedad para alcanzar la mayor altura. A medida que aumenta la altura del agua, el movimiento hacia la periferia ya no es ventajoso, porque la reducción de la energía potencial al trabajar con la fuerza centrífuga se compara con el aumento de la energía que trabaja contra la gravedad. Así, a una velocidad de rotación angular dada, una superficie cóncava representa la situación estable, y cuanto más rápida es la rotación, más cóncava es esta superficie. Si se detiene la rotación, la energía almacenada en el modelado de la superficie cóncava debe disiparse, por ejemplo, por fricción, antes de que se restablezca una superficie plana de equilibrio. A medida que aumenta la altura del agua, el movimiento hacia la periferia ya no es ventajoso, porque la reducción de la energía potencial al trabajar con la fuerza centrífuga se compara con el aumento de la energía que trabaja contra la gravedad. Así, a una velocidad de rotación angular dada, una superficie cóncava representa la situación estable, y cuanto más rápida es la rotación, más cóncava es esta superficie. Si se detiene la rotación, la energía almacenada en el modelado de la superficie cóncava debe disiparse, por ejemplo, por fricción, antes de que se restablezca una superficie plana de equilibrio. A medida que aumenta la altura del agua, el movimiento hacia la periferia ya no es ventajoso, porque la reducción de la energía potencial al trabajar con la fuerza centrífuga se compara con el aumento de la energía que trabaja contra la gravedad. Así, a una velocidad de rotación angular dada, una superficie cóncava representa la situación estable, y cuanto más rápida es la rotación, más cóncava es esta superficie. Si se detiene la rotación, la energía almacenada en el modelado de la superficie cóncava debe disiparse, por ejemplo, por fricción, antes de que se restablezca una superficie plana de equilibrio. una superficie cóncava representa la situación estable, y cuanto más rápida es la rotación, más cóncava es esta superficie. Si se detiene la rotación, la energía almacenada en el modelado de la superficie cóncava debe disiparse, por ejemplo, por fricción, antes de que se restablezca una superficie plana de equilibrio. una superficie cóncava representa la situación estable, y cuanto más rápida es la rotación, más cóncava es esta superficie. Si se detiene la rotación, la energía almacenada en el modelado de la superficie cóncava debe disiparse, por ejemplo, por fricción, antes de que se restablezca una superficie plana de equilibrio.

Para implementar una superficie de energía potencial constante cuantitativamente, deje que la altura del agua sea $${\ displaystyle h (r) \,}: entonces la energía potencial por unidad de masa aportada por la gravedad es $${\ displaystyle gh (r) \} y la energía potencial total por unidad de masa en la superficie es

$${\ displaystyle {U} = {U} _ {0} + gh (r) - {\ frac {1} {2}} \ Omega ^ {2} r ^ {2} \,}

con $${\ displaystyle {U} _ {0}}El nivel de energía de fondo independiente de r . En una situación estática (sin movimiento del fluido en el marco giratorio), esta energía es constante independientemente de la posición r . Requeriendo que la energía sea constante, obtenemos la forma parabólica :

$${\ displaystyle h (r) = {\ frac {\ Omega ^ {2}} {2g}} r ^ {2} + h (0) \,}

donde h (0) es la altura en r = 0 (el eje). Vea las figuras 1 y 2.

El principio de funcionamiento de la centrífuga también se puede entender simplemente en términos de esta expresión para la energía potencial, lo que demuestra que es favorable energéticamente cuando el volumen más alejado del eje de rotación está ocupado por la sustancia más pesada.

Hay varias analogías formales que se pueden hacer entre la electricidad, que es invisible al ojo, y comportamientos físicos más familiares, como el flujo de agua o el movimiento de dispositivos mecánicos .

En el caso de la capacitancia, una analogía con un capacitor en términos rectilíneos mecánicos es un resorte en el que la conformidad del resorte es análoga a la capacitancia . Así, en ingeniería eléctrica, un capacitor puede definirse como un componente eléctrico ideal que satisface esta ecuación V = (1 / C) )Idt donde:

V = voltaje medido en los terminales del capacitor

C = la capacitancia del capacitor

I = corriente que fluye entre los terminales del capacitor

t = tiempo

La ecuación citada anteriormente tiene la misma forma que la que describe un resorte ideal sin masa: F = (1 / k) ʃvdt donde:

F es la fuerza aplicada entre los dos extremos del resorte.

k es la conformidad del resorte definido como desplazamiento / fuerza

v es la velocidad (o velocidad) de un extremo del resorte, el otro extremo está fijo.

Tenga en cuenta que en el caso eléctrico, la corriente (I) se define como la tasa de cambio de carga (Q) con respecto al tiempo:

I = dQ / dt

Mientras que en el caso mecánico, la velocidad (v) se define como la tasa de cambio del desplazamiento (x) con respecto al tiempo:

v = dx / dt

Así, en esta analogía:

• La carga se representa por desplazamiento lineal ,
• la corriente está representada por la velocidad lineal ,
• Tensión por fuerza .
• tiempo por tiempo

Además, se aplican estas relaciones análogas:

• de energía . La energía almacenada en un resorte es 0.5x ^ 2 / k, mientras que la energía almacenada en un capacitor es 0.5Q ^ 2 / C.
• La energía eléctrica . Aquí hay una analogía entre el concepto mecánico de potencia como el producto escalar de la velocidad y el desplazamiento, y el concepto eléctrico de que en un circuito de CA con excitación sinusoidal, la potencia es el producto VIcos (ф) donde ф es el ángulo de fase entre V y Yo, medido en términos RMS .
• La resistencia eléctrica (R) es análoga al coeficiente de arrastre viscoso mecánico (la fuerza proporcional a la velocidad es análoga a la ley de Ohm : la tensión es proporcional a la corriente).
• La masa (m) es análoga a la inductancia (L), ya que F = m (dv / dt) mientras que V = LdI / dt. Por lo tanto, un inductor ideal con inductancia L es análogo a un cuerpo rígido con masa m.

Esta analogía del capacitor forma parte de la analogía de impedancia más completa de los sistemas mecánicos a los eléctricos.