MECÁNICA CLÁSICA

La mecánica celeste es la rama de la astronomía que se ocupa de los movimientos de los objetos en el espacio exterior . Históricamente, la mecánica celeste aplica los principios de la física( mecánica clásica ) a los objetos astronómicos, como las estrellasy los planetas , para producir datos de efemérides .

Como un campo de estudio astronómico, la mecánica celeste incluye los subcampos de la mecánica orbital , que se ocupa del lanzamiento y las órbitas de los satélites artificiales , y la teoría lunar , una especialidad que trata las complicaciones de la órbita de la Luna . La mecánica celeste moderna tiende a dividirse entre cinco amplios campos de estudio:

• Trayectorias de satélites artificiales ( astrodinámica ).
• movimientos de planetas mayores, planetas menores y satélites naturales en el Sistema Solar y otros sistemas estelares y sistemas de estrellas múltiples ampliamente espaciados (dinámica planetaria)
• el movimiento de las estrellas componentes y sus sistemas planetarios en sistemas de múltiples estrellas y grupos globulares muy espaciados (astrodinámica y dinámica estelar )
• Flujo de estrellas dentro y entre los cuerpos de grandes galaxias, galaxias enanas y cúmulos globulares ( dinámica estelar y dinámica galáctica)
• movimientos de galaxias y polvo y gas intergalácticos dentro de cúmulos de galaxias ( astrofísica computacional )

Todos los campos anteriores se superponen, pero a veces se los trata de forma separada, especialmente el estudio del movimiento de las estrellas dentro de las galaxias y las interacciones entre galaxias enteras , las cuales tienden a depender en gran medida de la mecánica del fluido (las estrellas enteras son partículas del "fluido") .

Historia [ editar ]

Para las teorías tempranas de las causas del movimiento planetario, vea Dinámicas de las esferas celestes .

La mecánica celeste analítica moderna comenzó con los Principia de Isaac Newton de 1687. El nombre de "mecánica celeste" es más reciente que eso. Newton escribió que el campo debería llamarse "mecánica racional". El término "dinámica" llegó poco después con Gottfried Leibniz , y más de un siglo después de Newton, Pierre-Simon Laplace introdujo el término "mecánica celeste". Antes de Kepler, había poca conexión entre la predicción exacta y cuantitativa de las posiciones planetarias, utilizando técnicas geométricas o aritméticas , y las discusiones contemporáneas sobre las causas físicas del movimiento de los planetas.

Johannes Kepler [ editar ]

Para obtener información detallada sobre cómo se pueden usar sus leyes de movimiento planetario, consulte las leyes de Kepler sobre el movimiento planetario y el problema de Kepler .

Johannes Kepler (1571-1630) fue el primero en integrar de cerca la astronomía geométrica predictiva, que había sido dominante desde Ptolomeo en el siglo II hasta Copérnico , con conceptos físicos para producir una Nueva Astronomía, Basada en Causas o Física Celestial en 1609. Su trabajo condujo a las leyes modernas de las órbitas planetarias , que desarrolló utilizando sus principios físicos y las observaciones planetarias hechas por Tycho Brahe . El modelo de Kepler mejoró en gran medida la precisión de las predicciones del movimiento planetario, años antes de que Isaac Newton desarrollara su ley de la gravitación en 1686.

Isaac Newton [ editar ]

Se le atribuye a Isaac Newton (25 de diciembre de 1642 a 31 de marzo de 1727) la introducción de la idea de que el movimiento de objetos en los cielos, como los planetas , el Sol y la Luna , y el movimiento de objetos en el suelo, como balas de cañón y caída de manzanas, podría ser descrito por el mismo conjunto de leyes físicas . En este sentido unificó las dinámicas celestes y terrestres . El uso de la ley de gravitación universal de Newton , que demuestra las Leyes de Kepler para el caso de una órbita circular, es simple. Las órbitas elípticas implican cálculos más complejos, que Newton incluyó en sus Principia .

Joseph-Louis Lagrange [ editar ]

Después de Newton, Lagrange (25 de enero de 1736 a 10 de abril de 1813) intentó resolver el problema de los tres cuerpos , analizó la estabilidad de las órbitas planetarias y descubrió la existencia de los puntos de Lagrangian . Lagrange también reformuló los principios de la mecánica clásica , enfatizando la energía más que la fuerza y ​​desarrollando un método para usar una única ecuación de coordenadas polares para describir cualquier órbita, incluso aquellas que son parabólicas e hiperbólicas. Esto es útil para calcular el comportamiento de los planetas y cometas y demás. Más recientemente, también se ha vuelto útil para calcular las trayectorias de las naves espaciales .

Simon Newcomb [ editar ]

Simon Newcomb (12 de marzo de 1835 a 11 de julio de 1909) fue un astrónomo canadiense-estadounidense que revisó la tabla de posiciones lunares de Peter Andreas Hansen . En 1877, asistido por George William Hill , recalculó todas las constantes astronómicas principales. Después de 1884, concibió con AMW Downing un plan para resolver mucha confusión internacional sobre el tema. Cuando asistió a una conferencia de estandarización en París , Francia, en mayo de 1886, el consenso internacional fue que todas las efemérides deberían basarse en los cálculos de Newcomb. Otra conferencia hasta 1950 confirmó las constantes de Newcomb como el estándar internacional.

Albert Einstein [ editar ]

Albert Einstein (14 de marzo de 1879 a 18 de abril de 1955) explicó la precesión anómala del perihelio de Mercurio en su artículo de 1916 La fundación de la teoría general de la relatividad . Esto llevó a los astrónomos a reconocer que la mecánica newtoniana no proporcionaba la mayor precisión. Se han observado púlsares binarios, el primero en 1974, cuyas órbitas no solo requieren el uso de la Relatividad General para su explicación, sino que su evolución demuestra la existencia de radiación gravitacional , un descubrimiento que condujo al Premio Nobel de Física de 1993.

Ejemplos de problemas [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser desafiado y eliminado . ( Abril de 2011 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

El movimiento celestial, sin fuerzas adicionales como el empuje de un cohete , se rige por la aceleración gravitacional de las masas debido a otras masas. Una simplificación es el problema de n- body , donde el problema supone un número n de masas esféricas simétricas. En ese caso, la integración de las aceleraciones se puede aproximar bien mediante sumas relativamente simples.

Ejemplos:

• Problema de 4 cuerpos: vuelo espacial a Marte (para partes del vuelo, la influencia de uno o dos cuerpos es muy pequeña, de modo que ahí tenemos un problema de 2 o 3 cuerpos; vea también la aproximación cónica parcheada )
• Problema de 3 cuerpos:
  • Cuasi-satélite
  • Vuelo espacial a, y estancia en un punto lagrangiano.

En el caso de que n = 2 ( problema de dos cuerpos ), la situación es mucho más simple que para n más grande . Se aplican varias fórmulas explícitas, donde en el caso más general, normalmente solo son posibles soluciones numéricas. Es una simplificación útil que a menudo es aproximadamente válida.

Ejemplos:

• Una estrella binaria , por ejemplo, Alpha Centauri (aproximadamente la misma masa)
• Un asteroide binario , por ejemplo, 90 Antiope (aproximadamente la misma masa)

Otra simplificación se basa en las "suposiciones estándar en astrodinámica", que incluyen que un cuerpo, el cuerpo en órbita , es mucho más pequeño que el otro, el cuerpo central . Esto también es a menudo aproximadamente válido.

Ejemplos:

• Sistema solar que orbita el centro de la Vía Láctea.
• Un planeta orbitando el Sol.
• Una luna orbitando un planeta.
• Una nave espacial que orbita la Tierra, una luna o un planeta (en los últimos casos, la aproximación solo se aplica después de llegar a esa órbita)

Teoría de la perturbación [ editar ]

Artículo principal: Teoría de la perturbación.

La teoría de la perturbación comprende métodos matemáticos que se utilizan para encontrar una solución aproximada a un problema que no se puede resolver exactamente. (Está estrechamente relacionado con los métodos utilizados en el análisis numérico , que son antiguos ). El uso más antiguo de la teoría moderna de la perturbación fue tratar los problemas matemáticos de la mecánica celeste, que de otro modo serían imposibles de resolver: la solución de Newton para la órbita de la Luna , que se mueve notablemente diferente de una simple elipse de Kepler debido a la gravitación competitiva de la Tierra y el Sol .

Los métodos de perturbación comienzan con una forma simplificada del problema original, que se elige cuidadosamente para resolverlo exactamente. En la mecánica celeste, esto suele ser una elipse de Kepler , que es correcta cuando solo hay dos cuerpos gravitantes (es decir, la Tierra y la Luna ), o una órbita circular, que solo es correcta en casos especiales de movimiento de dos cuerpos, pero a menudo es lo suficientemente cerca para el uso práctico.

El problema resuelto, pero simplificado, se "perturba" para hacer que sus ecuaciones de tasa de cambio de tiempo para la posición del objeto se acerquen más a los valores del problema real, como la atracción gravitacional de un tercer cuerpo más distante (el Sol ). Los leves cambios que resultan de los términos en las ecuaciones, que pueden haberse simplificado una vez más, se utilizan como correcciones a la solución original. Debido a que las simplificaciones se realizan en cada paso, las correcciones nunca son perfectas, pero incluso un ciclo de correcciones a menudo proporciona una solución aproximada al problema real notablemente mejor.

No hay ningún requisito para detenerse en un solo ciclo de correcciones. Una solución parcialmente corregida puede reutilizarse como el nuevo punto de partida para otro ciclo de perturbaciones y correcciones. En principio, para la mayoría de los problemas, el reciclaje y el refinamiento de soluciones anteriores para obtener una nueva generación de soluciones mejores podría continuar indefinidamente, con cualquier grado finito de precisión deseado.

La dificultad común con el método es que las correcciones generalmente hacen que las nuevas soluciones progresivamente sean mucho más complicadas, por lo que cada ciclo es mucho más difícil de administrar que el ciclo anterior de correcciones. Se dice que Newton ha dicho, con respecto al problema de la órbita de la Luna "Me duele la cabeza". ^[1]

Este procedimiento general, que comienza con un problema simplificado y agrega gradualmente correcciones que hacen que el punto de partida del problema corregido se acerque más a la situación real, es una herramienta matemática ampliamente utilizada en ciencias avanzadas e ingeniería. Es la extensión natural del método de "adivinar, verificar y corregir" utilizado antiguamente con números .

Ver tambien [ editar ]

• Portal de astronomia

• La astrometría es una parte de la astronomía que trata de medir las posiciones de las estrellas y otros cuerpos celestes, sus distancias y movimientos.
• La astrodinámica es el estudio y la creación de órbitas, especialmente las de satélites artificiales.
• La navegación celestial es una técnica de fijación de posición que fue el primer sistema diseñado para ayudar a los navegantes a ubicarse en un océano sin rasgos distintivos.
• La dinámica de las esferas celestes concierne a las explicaciones pre-newtonianas de las causas de los movimientos de las estrellas y los planetas.
• Efemérides es una compilación de posiciones de objetos astronómicos naturales, así como satélites artificiales en el cielo en un momento o momentos determinados.
• Gravitación
• El análisis numérico es una rama de las matemáticas, iniciada por mecánicos celestes, para calcular respuestas numéricas aproximadas (como la posición de un planeta en el cielo) que son demasiado difíciles de resolver con una fórmula general y exacta.
• Crear un modelo numérico del sistema solar era el objetivo original de la mecánica celeste, y solo se ha logrado de manera imperfecta. Sigue motivando la investigación.
• Una órbita es el camino que hace un objeto, alrededor de otro, mientras está bajo la influencia de una fuente de fuerza centrípeta, como la gravedad.
• Los elementos orbitales son los parámetros necesarios para especificar de forma única una órbita de dos cuerpos newtoniana.
• Órbita oscilante es la órbita Kepleriana temporal sobre un cuerpo central en el que un objeto continuaría, si no existieran otras perturbaciones.
• Movimiento retrógrado
• Satélite es un objeto que orbita a otro objeto (conocido como su principal). El término se usa a menudo para describir un satélite artificial (a diferencia de los satélites naturales o lunas). El nombre común luna (sin mayúscula) se usa para significar cualquier satélite natural de los otros planetas.
• Fuerza de marea
• Las efemérides de desarrollo del Laboratorio de Propulsión a Chorro (JPL DE) es un modelo ampliamente utilizado del sistema solar, que combina la mecánica celeste con el análisis numérico y los datos astronómicos y de naves espaciales.
• Dos soluciones, llamadas VSOP82 y VSOP87 son versiones de una teoría matemática para las órbitas y posiciones de los planetas principales, que buscan proporcionar posiciones precisas durante un período prolongado de tiempo.
• La teoría lunar intenta dar cuenta de los movimientos de la Luna.

centro de masa de una distribución de masa en el espacio es el único punto donde la posición relativa ponderada de la masa distribuida es cero, o el punto donde se aplica una fuerza, se mueve en la dirección de la fuerza sin girar. . La distribución de masa se equilibra alrededor del centro de masa y el promedio de las coordenadas de posición ponderadas de la masa distribuida define sus coordenadas. Cálculos en mecánica.A menudo se simplifican cuando se formulan con respecto al centro de masa. Es un punto hipotético donde se puede suponer que toda la masa de un objeto está concentrada para visualizar su movimiento. En otras palabras, el centro de masa es el equivalente de partícula de un objeto dado para la aplicación de las leyes del movimiento de Newton.

En el caso de un solo cuerpo rígido , el centro de masa se fija en relación con el cuerpo, y si el cuerpo tiene una densidad uniforme, se ubicará en el centroide . El centro de masa puede estar ubicado fuera del cuerpo físico, como es a veces el caso de objetos huecos o de forma abierta, como una herradura . En el caso de una distribución de cuerpos separados, como los planetas del Sistema Solar , el centro de masa puede no corresponder a la posición de ningún miembro individual del sistema.

El centro de masa es un punto de referencia útil para los cálculos en mecánica que involucran masas distribuidas en el espacio, como el momento lineal y angular de los cuerpos planetarios y la dinámica de cuerpos rígidos . En la mecánica orbital , las ecuaciones de movimiento de los planetas se formulan como masas puntuales ubicadas en los centros de masa. El marco del centro de masa es un marco de inercia en el que el centro de masa de un sistema está en reposo con respecto al origen del sistema de coordenadas.

Historia [ editar ]

El concepto de "centro de masa" en forma de centro de gravedad fue presentado por primera vez por el gran físico, matemático e ingeniero griego antiguo Arquímedes de Siracusa . Trabajó con supuestos simplificados acerca de la gravedad que equivalen a un campo uniforme, llegando así a las propiedades matemáticas de lo que ahora llamamos el centro de masa. Arquímedes demostró que el par que se ejerce sobre una palanca.por pesos que descansan en varios puntos a lo largo de la palanca es lo mismo que lo sería si todos los pesos se movieran a un solo punto: su centro de masa. En trabajos sobre cuerpos flotantes, demostró que la orientación de un objeto flotante es la que hace que su centro de masa sea lo más bajo posible. Desarrolló técnicas matemáticas para encontrar los centros de masa de objetos de densidad uniforme de varias formas bien definidas. ^[1]

Los matemáticos posteriores que desarrollaron la teoría del centro de masas incluyen a Pappus de Alejandría , Guido Ubaldi , Francesco Maurolico , ^[2] Federico Commandino , ^[3] Simon Stevin , ^[4] Luca Valerio , ^[5] Jean-Charles de la Faille , Paul Guldin , ^[6] John Wallis , Louis Carré , Pierre Varignon y Alexis Clairaut . ^[7]

La segunda ley de Newton está reformulada con respecto al centro de masa en la primera ley de Euler . ^[8]

Diagrama de un juguete educativo que se balancea en un punto: el centro de masa (C) se coloca debajo de su soporte (P)

Definición [ editar ]

El centro de masa es el único punto en el centro de una distribución de masa en el espacio que tiene la propiedad de que los vectores de posición ponderados relativos a este punto se suman a cero. En analogía con las estadísticas, el centro de masa es la ubicación media de una distribución de masa en el espacio.

Un sistema de partículas [ editar ]

En el caso de un sistema de partículas P _i , i = 1,…,  n  , cada una con masa m _i que se encuentra en el espacio con las coordenadas r _i , i = 1,…,  n  , las coordenadas R del centro de masa satisfacer la condición

$${\ displaystyle \ sum _ {i = 1} ^ {n} m_ {i} (\ mathbf {r} _ {i} - \ mathbf {R}) = 0.}

Resolviendo esta ecuación para R se obtiene la fórmula.

$${\ displaystyle \ mathbf {R} = {\ frac {1} {M}} \ sum _ {i = 1} ^ {n} m_ {i} \ mathbf {r} _ {i},}

donde M es la suma de las masas de todas las partículas.

Un volumen continuo [ editar ]

Si la distribución de masa es continua con la densidad ρ ( r ) dentro de un sólido Q , entonces la integral de las coordenadas de posición ponderadas de los puntos en este volumen en relación con el centro de masa R sobre el volumen V es cero, es decir

$${\ displaystyle \ iiint \ limits _ {Q} \ rho (\ mathbf {r}) (\ mathbf {r} - \ mathbf {R}) dV = 0.}

Resolver esta ecuación para las coordenadas R para obtener

$${\ displaystyle \ mathbf {R} = {\ frac {1} {M}} \ iiint \ limits _ {Q} \ rho (\ mathbf {r}) \ mathbf {r} dV,}

donde M es la masa total en el volumen.

Si una distribución de masa continua tiene una densidad uniforme , lo que significa que ρ es constante, entonces el centro de masa es el mismo que el centroide del volumen. ^[9]

Coordenadas baricéntricas [ editar ]

Más información: Sistema de coordenadas baricéntrico.

Las coordenadas R del centro de masa de un sistema de dos partículas, P ₁ y P ₂ , con masas m ₁ y m ₂ están dadas por

$${\ displaystyle \ mathbf {R} = {\ frac {1} {m_ {1} + m_ {2}}} (m_ {1} \ mathbf {r} _ {1} + m_ {2} \ mathbf {r } _ {2}).}

Deje que el porcentaje de la masa total dividida entre estas dos partículas varíe entre 100% P ₁ y 0% P ₂ hasta 50% P ₁ y 50% P ₂ hasta 0% P ₁ y 100% P ₂ , luego el centro de masa R Se mueve a lo largo de la línea de P ₁ a P ₂ . Los porcentajes de masa en cada punto se pueden ver como coordenadas proyectivas del punto Ren esta línea, y se denominan coordenadas baricéntricas. Otra forma de interpretar el proceso aquí es el equilibrio mecánico de momentos sobre un punto arbitrario. El numerador da el momento total que luego se equilibra con una fuerza total equivalente en el centro de masa. Esto se puede generalizar a tres puntos y cuatro puntos para definir coordenadas proyectivas en el plano y en el espacio, respectivamente.

Sistemas con condiciones de contorno periódicas [ editar ]

Para partículas en un sistema con condiciones límite periódicas, dos partículas pueden ser vecinas aunque estén en lados opuestos del sistema. Esto ocurre a menudo en simulaciones de dinámica molecular , por ejemplo, en las que los grupos se forman en ubicaciones aleatorias y, a veces, los átomos vecinos cruzan el límite periódico. Cuando un grupo se extiende a ambos lados del límite periódico, un cálculo ingenuo del centro de masa será incorrecto. Un método generalizado para calcular el centro de masa para sistemas periódicos es tratar a cada coordenada, x y y y / o z , como si fuera en un círculo en lugar de una línea. ^[10] El cálculo toma la x de cada partícula. coordinar y mapearlo a un ángulo,

$${\ displaystyle \ theta _ {i} = {\ frac {x_ {i}} {x_ {max}}} 2 \ pi}

donde x _max es el tamaño del sistema en la dirección x y$${\ displaystyle x_ {i} \ en [0, x_ {max})}. Desde este ángulo, dos nuevos puntos.$${\ displaystyle (\ xi _ {i}, \ zeta _ {i})} Se puede generar, que puede ser ponderada por la masa de la partícula. $${\ displaystyle x_ {i}} para el centro de masa o dado un valor de 1 para el centro geométrico:

$${\ displaystyle \ xi _ {i} = \ cos (\ theta _ {i})}

$${\ displaystyle \ zeta _ {i} = \ sin (\ theta _ {i})}

En el $${\ displaystyle (\ xi, \ zeta)} plano, estas coordenadas se encuentran en un círculo de radio 1. De la colección de $${\ displaystyle \ xi _ {i}} y $${\ displaystyle \ zeta _ {i}} Valores de todas las partículas, los promedios. $${\ displaystyle {\ overline {\ xi}}} y $${\ displaystyle {\ overline {\ zeta}}} se calculan

$${\ displaystyle {\ overline {\ xi}} = {\ frac {1} {M}} \ sum _ {i = 1} ^ {n} m_ {i} \ xi _ {i},}

$${\ displaystyle {\ overline {\ zeta}} = {\ frac {1} {M}} \ sum _ {i = 1} ^ {n} m_ {i} \ zeta _ {i},}

donde M es la suma de las masas de todas las partículas.

Estos valores se asignan de nuevo en un nuevo ángulo, $${\ displaystyle {\ overline {\ theta}}}, a partir de la cual se puede obtener la coordenada xdel centro de masa:

$${\ displaystyle {\ overline {\ theta}} = \ mathrm {atan2} (- {\ overline {\ zeta}}, - {\ overline {\ xi}}) + \ pi}

$${\ displaystyle x_ {com} = x_ {max} {\ frac {\ overline {\ theta}} {2 \ pi}}}

El proceso se puede repetir en todas las dimensiones del sistema para determinar el centro de masa completo. La utilidad del algoritmo es que permite a las matemáticas determinar dónde está el "mejor" centro de masa, en lugar de adivinar o usar el análisis de conglomerados para "desplegar" un conglomerado que se extiende a lo largo de los límites periódicos. Si ambos valores medios son cero,$${\ displaystyle ({\ overline {\ xi}}, {\ overline {\ zeta}}) = (0,0)}, entonces $${\ displaystyle {\ overline {\ theta}}}es indefinido. Este es un resultado correcto, porque solo ocurre cuando todas las partículas están espaciadas exactamente de manera uniforme. En esa condición, sus coordenadas x son matemáticamente idénticas en un sistema periódico .

Centro de gravedad [ editar ]

Artículo principal: Centros de gravedad en campos no uniformes.

El centro de gravedad de un cuerpo es el punto alrededor del cual el torque resultante debido a las fuerzas de gravedad se desvanece. Donde un campo de gravedad puede considerarse uniforme, el centro de masa y el centro de gravedad serán los mismos. Sin embargo, para satélites en órbita alrededor de un planeta, en ausencia de otros pares de torsión aplicados a un satélite, la ligera variación (gradiente) en el campo gravitacional entre más cercano (más fuerte) y más lejos (más débil) que el planeta puede llevar a un par que tenderá a alinear el satélite de modo que su eje largo sea vertical. En tal caso, es importante hacer la distinción entre el centro de gravedad y el centro de masa. Cualquier desplazamiento horizontal entre los dos resultará en un par aplicado.

Es útil señalar que el centro de masa es una propiedad fija para un cuerpo rígido dado (por ejemplo, sin movimiento o articulación), mientras que el centro de gravedad puede, además, depender de su orientación en una gravedad no uniforme. campo. En este último caso, el centro de gravedad siempre estará ubicado algo más cerca del cuerpo atractivo principal en comparación con el centro de masas, y por lo tanto cambiará su posición en el cuerpo de interés a medida que cambie su orientación.

En el estudio de la dinámica de los aviones, vehículos y buques, las fuerzas y los momentos deben resolverse en relación con el centro de masas. Eso es cierto independientemente de si la gravedad en sí misma es una consideración. El referirse al centro de masas como el centro de gravedad es una especie de coloquialismo, pero es de uso común y cuando los efectos del gradiente de gravedad son despreciables, el centro de gravedad y el centro de masas son los mismos y se usan indistintamente.

En física, los beneficios de usar el centro de masa para modelar una distribución de masa se pueden ver considerando la resultante de las fuerzas de gravedad en un cuerpo continuo. Considere un cuerpo Q de volumen V con densidad ρ ( r ) en cada punto r en el volumen. En un campo de gravedad paralelo, la fuerza f en cada punto r viene dada por,

$${\ displaystyle \ mathbf {f} (\ mathbf {r}) = - dm \, ​​g {\ vec {k}} = - \ rho (\ mathbf {r}) dV \, g {\ vec {k}} ,}

donde dm es la masa en el punto r , g es la aceleración de la gravedad y k es un vector unitario que define la dirección vertical. Elija un punto de referencia R en el volumen y calcule la fuerza y el par resultantes en este punto,

$${\ displaystyle \ mathbf {F} = \ iiint \ limits _ {Q} \ mathbf {f} (\ mathbf {r}) = \ iiint \ limits _ {Q} \ rho (\ mathbf {r}) dV (- g {\ vec {k}}) = - Mg {\ vec {k}},}

y

$${\ displaystyle \ mathbf {T} = \ iiint \ limits _ {Q} (\ mathbf {r} - \ mathbf {R}) \ times \ mathbf {f} (\ mathbf {r}) = \ iiint \ limits _ {Q} (\ mathbf {r} - \ mathbf {R}) \ times (-g \ rho (\ mathbf {r}) dV {\ vec {k}}) = \ left (\ iiint \ limits _ {Q } \ rho (\ mathbf {r}) (\ mathbf {r} - \ mathbf {R}) dV \ right) \ times (-g {\ vec {k}}).}

Si el punto de referencia R se elige de modo que sea el centro de masa, entonces

$${\ displaystyle \ iiint \ limits _ {Q} \ rho (\ mathbf {r}) (\ mathbf {r} - \ mathbf {R}) dV = 0,}

lo que significa el par resultante T = 0. Debido a que el torque resultante es cero, el cuerpo se moverá como si fuera una partícula con su masa concentrada en el centro de la masa.

Al seleccionar el centro de gravedad como el punto de referencia para un cuerpo rígido, las fuerzas de la gravedad no harán que el cuerpo gire, lo que significa que el peso del cuerpo puede considerarse concentrado en el centro de la masa.

Momento lineal y angular [ editar ]

El momento lineal y angular de una colección de partículas se puede simplificar midiendo la posición y la velocidad de las partículas con respecto al centro de masa. Deje que el sistema de partículas P _i , i = 1, ..., n de masas m _i esté ubicado en las coordenadas r _i con velocidades v _i . Seleccione un punto de referencia R y calcule los vectores de posición relativa y velocidad,

$${\ displaystyle \ mathbf {r} _ {i} = (\ mathbf {r} _ {i} - \ mathbf {R}) + \ mathbf {R}, \ quad \ mathbf {v} _ {i} = { \ frac {d} {dt}} (\ mathbf {r} _ {i} - \ mathbf {R}) + \ mathbf {v}.}

Los vectores de momento lineal y angular totales relativos al punto de referencia R son

$${\ displaystyle \ mathbf {p} = {\ frac {d} {dt}} \ left (\ sum _ {i = 1} ^ {n} m_ {i} (\ mathbf {r} _ {i} - \ mathbf {R}) \ derecha) + \ izquierda (\ sum _ {i = 1} ^ {n} m_ {i} \ derecha) \ mathbf {v},}

y

$${\ displaystyle \ mathbf {L} = \ sum _ {i = 1} ^ {n} m_ {i} (\ mathbf {r} _ {i} - \ mathbf {R}) \ times {\ frac {d} {dt}} (\ mathbf {r} _ {i} - \ mathbf {R}) + \ left (\ sum _ {i = 1} ^ {n} m_ {i} (\ mathbf {r} _ {i } - \ mathbf {R}) \ right) \ times \ mathbf {v}.}

Si se elige R como el centro de masa, estas ecuaciones se simplifican para

$${\ displaystyle \ mathbf {p} = m \ mathbf {v}, \ quad \ mathbf {L} = \ sum _ {i = 1} ^ {n} m_ {i} (\ mathbf {r} _ {i} - \ mathbf {R}) \ times {\ frac {d} {dt}} (\ mathbf {r} _ {i} - \ mathbf {R}),}

donde m es la masa total de todas las partículas, p es el momento lineal y L es el momento angular

La Ley de Conservación del Momento predice que para cualquier sistema no sometido a fuerzas externas, el impulso del sistema permanecerá constante, lo que significa que el centro de masa se moverá con velocidad constante. Esto se aplica a todos los sistemas con fuerzas internas clásicas, incluidos campos magnéticos, campos eléctricos, reacciones químicas, etc. Más formalmente, esto es cierto para cualquier fuerza interna que se cancele de acuerdo con la Tercera Ley de Newton . ^[11]

Localizando el centro de masa [ editar ]

Artículo principal: Localización del centro de masa.

Método de línea vertical

La determinación experimental del centro de masa de un cuerpo utiliza las fuerzas de gravedad sobre el cuerpo y se basa en el hecho de que en el campo de gravedad paralelo cerca de la superficie de la tierra el centro de masa es el mismo que el centro de gravedad.

El centro de masa de un cuerpo con un eje de simetría y densidad constante debe estar sobre este eje. Por lo tanto, el centro de masa de un cilindro circular de densidad constante tiene su centro de masa en el eje del cilindro. De la misma manera, el centro de masa de un cuerpo esféricamente simétrico de densidad constante está en el centro de la esfera. En general, para cualquier simetría de un cuerpo, su centro de masa será un punto fijo de esa simetría. ^[12]

En dos dimensiones [ editar ]

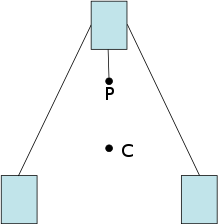
Un método experimental para ubicar el centro de masa es suspender el objeto desde dos ubicaciones y colocar líneas verticales desde los puntos de suspensión. La intersección de las dos líneas es el centro de masa. ^[13]

La forma de un objeto ya podría estar determinada matemáticamente, pero puede ser demasiado compleja para usar una fórmula conocida. En este caso, se puede subdividir la forma compleja en formas más simples y elementales, cuyos centros de masa son fáciles de encontrar. Si la masa total y el centro de masa se pueden determinar para cada área, entonces el centro de masa del conjunto es el promedio ponderado de los centros. ^[14] Este método puede funcionar incluso para objetos con agujeros, que se pueden contabilizar como masas negativas. ^[15]

Se puede usar un desarrollo directo del planímetro conocido como un integraph, o integerometer, para establecer la posición del centroide o centro de masa de una forma bidimensional irregular. Este método se puede aplicar a una forma con un límite irregular, liso o complejo donde otros métodos son demasiado difíciles. Fue utilizado regularmente por los constructores de barcos para comparar con el desplazamiento requerido y el centro de flotabilidad de un barco, y garantizar que no se volcara. ^[16] [17]

En tres dimensiones [ editar ]

Un método experimental para ubicar las coordenadas tridimensionales del centro de masa comienza apoyando el objeto en tres puntos y midiendo las fuerzas, F ₁ , F ₂ y F ₃ que resisten el peso del objeto.$${\ displaystyle \ mathbf {W} = -W \ mathbf {\ hat {k}}} ($${\ displaystyle \ mathbf {\ hat {k}}}es el vector unitario en la dirección vertical). Sean r ₁ , r ₂ y r ₃ las coordenadas de posición de los puntos de apoyo, luego las coordenadas R del centro de masa satisfacen la condición de que el par resultante sea cero,

$${\ displaystyle \ mathbf {T} = (\ mathbf {r} _ {1} - \ mathbf {R}) \ times \ mathbf {F} _ {1} + (\ mathbf {r} _ {2} - \ mathbf {R}) \ times \ mathbf {F} _ {2} + (\ mathbf {r} _ {3} - \ mathbf {R}) \ times \ mathbf {F} _ {3} = 0,}

o

$${\ displaystyle \ mathbf {R} \ times (-W \ mathbf {\ hat {k}}) = \ mathbf {r} _ {1} \ times \ mathbf {F} _ {1} + \ mathbf {r} _ {2} \ times \ mathbf {F} _ {2} + \ mathbf {r} _ {3} \ times \ mathbf {F} _ {3}.}

Esta ecuación produce las coordenadas del centro de masa R * en el plano horizontal como,

$${\ displaystyle \ mathbf {R} ^ {*} = - {\ frac {1} {W}} \ mathbf {\ hat {k}} \ times (\ mathbf {r} _ {1} \ times \ mathbf { F} _ {1} + \ mathbf {r} _ {2} \ times \ mathbf {F} _ {2} + \ mathbf {r} _ {3} \ times \ mathbf {F} _ {3}). }

El centro de masa se encuentra en la línea vertical L, dada por

$${\ displaystyle \ mathbf {L} (t) = \ mathbf {R} ^ {*} + t \ mathbf {\ hat {k}}.}

Las coordenadas tridimensionales del centro de masa se determinan realizando este experimento dos veces con el objeto posicionado de modo que estas fuerzas se midan para dos planos horizontales diferentes a través del objeto. El centro de masa será la intersección de las dos líneas L ₁ y L ₂ obtenidas de los dos experimentos.

Aplicaciones [ editar ]

Diseños de ingeniería [ editar ]

Aplicaciones automotrices [ editar ]

Los ingenieros intentan diseñar un automóvil deportivo de modo que su centro de masa se reduzca para hacer que el auto se maneje mejor, es decir, mantener la tracción mientras se ejecutan giros relativamente agudos.

El perfil bajo característico del Humvee militar de EE. UU. Fue diseñado en parte para permitir que se incline más lejos que los vehículos más altos, sin vuelco , porque su centro de masa bajo permanecería sobre el espacio delimitado por las cuatro ruedas incluso en ángulos alejados de la horizontal.

Aeronáutica [ editar ]

Artículo principal: Centro de gravedad de una aeronave.

El centro de masa es un punto importante en una aeronave , que afecta significativamente la estabilidad de la aeronave. Para garantizar que la aeronave sea lo suficientemente estable como para estar segura para volar, el centro de masa debe estar dentro de los límites especificados. Si el centro de masa está delante del límite delantero, la aeronave será menos maniobrable, posiblemente hasta el punto de no poder girar para el despegue o la bengala para el aterrizaje. ^[18] Si el centro de masa está detrás del límite de popa, el avión será más maniobrable, pero también menos estable, y posiblemente tan inestable que sea imposible volar. El momento en que el brazo del elevador también se reducirá, lo que hace que sea más difícil recuperarse de una condición bloqueada . ^[19]

Para los helicópteros en vuelo estacionario , el centro de masa está siempre directamente debajo de la cabezadel rotor . En vuelo hacia adelante, el centro de masa avanzará para equilibrar el par de tono negativo producido al aplicar el control cíclico para impulsar el helicóptero hacia adelante; en consecuencia, un helicóptero de crucero vuela "nariz abajo" en vuelo nivelado. ^[20]

Astronomía [ editar ]

Artículo principal: Baricentro

Dos cuerpos orbitando su baricentro (cruz roja)

El centro de masa juega un papel importante en la astronomía y la astrofísica, donde se le conoce comúnmente como el baricentro . El baricentro es el punto entre dos objetos donde se equilibran; es el centro de masa donde dos o más cuerpos celestes se orbitan entre sí. Cuando una luna orbita un planeta , o un planeta orbita una estrella , ambos cuerpos están orbitando alrededor de un punto que se encuentra alejado del centro del cuerpo primario (más grande). ^[21] Por ejemplo, la Luna no orbita el centro exacto de la Tierra, pero un punto en una línea entre el centro de la Tierra y la Luna, aproximadamente 1,710 km (1,062 millas) debajo de la superficie de la Tierra, donde se equilibran sus respectivas masas. Este es el punto alrededor del cual la Tierra y la Luna orbitan mientras viajan alrededor del Sol . Si las masas son más similares, por ejemplo, Plutón y Caronte , el baricentro caerá fuera de ambos cuerpos.

Movimiento corporal [ editar ]

Centro de masa / gravedad estimado de un saltador alto que realiza un Flop de Fosbury. Tenga en cuenta que está debajo de la barra en esta posición.

Cuando los saltadores altos realizan un " Flop de Fosbury ", doblan sus respectivos cuerpos de tal manera que limpian la barra mientras que sus respectivos centros de masa no lo hacen necesariamente. ^[22] Debido a que es la altura del centro de gravedad (en lugar de la parte más alta del cuerpo) lo que limita la inversión mínima de energía para "limpiar" la barra, "pasar por encima" de la barra puede reducir la energía gastada en la propulsión el cuerpo hacia arriba.

Artículo principal: Kinesiología.

En kinesiología y biomecánica, el centro de masa es un parámetro importante que ayuda a las personas a comprender su locomoción humana. Típicamente, el centro de masa de un humano se detecta con uno de dos métodos: el método de la tabla de reacción es un análisis estático que involucra a la persona acostada en ese instrumento, y el uso de su ecuación de equilibrio estático para encontrar su centro de masa; el método de segmentación se basa en una solución matemática basada en el principio físico de que la suma de los pares de torsiones de las secciones individuales del cuerpo, en relación con un eje específico , debe ser igual al par de torsión de todo el sistema que constituye el cuerpo, medidoEn relación con el mismo eje.