MECÁNICA CLÁSICA

Izquierda: dos cuerpos con una masa similar que orbitan un baricentro común externo a ambos cuerpos, con órbitas elípticas , típicas de las estrellas binarias. A la derecha: dos cuerpos con una "leve" diferencia en masa orbitando un baricentro común. Los tamaños y este tipo de órbita son similares al sistema de Plutón-Caronte (en el que el baricentro es externo a ambos cuerpos) y al sistema Tierra - Luna , donde el baricentro es interno al cuerpo más grande.

En la mecánica clásica , el problema de los dos cuerposes determinar el movimiento de las partículas de dos puntos que interactúan solo entre sí. Los ejemplos comunes incluyen un satélite que orbita un planeta , un planeta que orbita una estrella , dos estrellas que seorbitan entre sí (una estrella binaria ) y un electrón clásico que orbita un núcleo atómico (aunque para resolver el sistema de electrón / núcleo de 2 cuerpos correctamente, un cuanto Se debe utilizar aproximación mecánica).

El problema de dos cuerpos se puede reformular como dos problemas de un solo cuerpo , uno trivial y uno que involucra resolver el movimiento de una partícula en un potencial externo . Dado que muchos problemas de un solo cuerpo pueden resolverse exactamente, el problema de dos cuerpos correspondiente también puede resolverse. Por el contrario, el problema de los tres cuerpos (y, más generalmente, el problema de los n cuerpos para n  ≥ 3) no se puede resolver en términos de primeras integrales, excepto en casos especiales.

Reducción a dos problemas independientes de un solo cuerpo [ editar ]

Jacobi coordina para el problema de dos cuerpos; Coordenadas de Jacobi son$${\ displaystyle {\ boldsymbol {R}} = {\ frac {m_ {1}} {M}} {\ boldsymbol {x}} _ {1} + {\ frac {m_ {2}} {M}} { \ boldsymbol {x}} _ {2}}y $${\ displaystyle {\ boldsymbol {r}} = {\ boldsymbol {x}} _ {1} - {\ boldsymbol {x}} _ {2}} con $${\ displaystyle M = m_ {1} + m_ {2} \}. ^[1]

Sean x ₁ y x ₂ las posiciones vectoriales de los dos cuerpos, y m ₁ y m ₂ son sus masas. El objetivo es determinar las trayectorias x ₁ ( t ) y x ₂ ( t ) para todos los tiempos t , dadas las posiciones iniciales x ₁ ( t  = 0) y x ₂ ( t  = 0) y las velocidades iniciales v ₁ ( t  = 0) y v ₂ ( t  = 0).

Cuando se aplica a las dos masas, la segunda ley de Newton establece que

$${\ displaystyle \ mathbf {F} _ {12} (\ mathbf {x} _ {1}, \ mathbf {x} _ {2}) = m_ {1} {\ ddot {\ mathbf {x}}} _ {1} \ quad \ quad \ quad (\ mathrm {Ecuación} \ 1)}

$${\ displaystyle \ mathbf {F} _ {21} (\ mathbf {x} _ {1}, \ mathbf {x} _ {2}) = m_ {2} {\ ddot {\ mathbf {x}}} _ {2} \ quad \ quad \ quad (\ mathrm {Ecuación} \ 2)}

donde F ₁₂ es la fuerza en la masa 1 debido a sus interacciones con la masa 2, y F ₂₁ es la fuerza en la masa 2 debido a sus interacciones con la masa 1. Los dos puntos en la parte superior de los vectores de posición x denotan su segunda derivada con respecto a tiempo, o sus vectores de aceleración.

Sumar y restar estas dos ecuaciones las desacopla en dos problemas de un solo cuerpo, que se pueden resolver de forma independiente. Agregar las ecuaciones (1) y (2) da como resultado una ecuación que describe el movimiento del centro de masa ( baricentro ). Por el contrario, restar la ecuación (2) de la ecuación (1) da como resultado una ecuación que describe cómo el vector r  =  x ₁  -  x ₂ entre las masas cambia con el tiempo. Las soluciones de estos problemas independientes de un solo cuerpo se pueden combinar para obtener las soluciones para las trayectorias x ₁ ( t ) y x ₂ ( t).

Centro de movimiento de masas (1er problema de un solo cuerpo) [ editar ]

Dejar $${\ displaystyle \ mathbf {R}}Ser la posición del centro de masa ( baricentro ) del sistema. Suma de las ecuaciones de fuerza (1) y (2) rendimientos.

$${\ displaystyle m_ {1} {\ ddot {\ mathbf {x}}} _ {1} + m_ {2} {\ ddot {\ mathbf {x}}} _ {2} = (m_ {1} + m_ {2}) {\ ddot {\ mathbf {R}}} = \ mathbf {F} _ {12} + \ mathbf {F} _ {21} = 0}

donde hemos usado la tercera ley de Newton F ₁₂  = - F ₂₁ y donde

$${\ displaystyle {\ ddot {\ mathbf {R}}} \ equiv {\ frac {m_ {1} {\ ddot {\ mathbf {x}}} _ {1} + m_ {2} {\ ddot {\ mathbf {x}}} _ {2}} {m_ {1} + m_ {2}}}.}

La ecuación resultante:

$${\ displaystyle {\ ddot {\ mathbf {R}}} = 0}

muestra que la velocidad V  =  d R / dt del centro de masa es constante, de lo que se deduce que el momento total m ₁ v ₁  +  m ₂ v ₂ también es constante ( conservación del momento ). Por lo tanto, la posición R ( t ) del centro de masa se puede determinar en todo momento a partir de las posiciones y velocidades iniciales.

Desplazamiento del movimiento vectorial (segundo problema de un solo cuerpo) [ editar ]

Dividiendo ambas ecuaciones de fuerza por las masas respectivas, restando la segunda ecuación de la primera y reorganizando da la ecuación

$${\ displaystyle {\ ddot {\ mathbf {r}}} = {\ ddot {\ mathbf {x}}} _ {1} - {\ ddot {\ mathbf {x}}} _ {2} = \ left ( {\ frac {\ mathbf {F} _ {12}} {m_ {1}}} - {\ frac {\ mathbf {F} _ {21}} {m_ {2}}} \ right) = \ left ( {\ frac {1} {m_ {1}}} + {\ frac {1} {m_ {2}}} \ derecha) \ mathbf {F} _ {12}}

donde hemos usado nuevamente la tercera ley de Newton F ₁₂  = - F ₂₁ y donde r es el vector de desplazamientode la masa 2 a la masa 1, como se definió anteriormente.

La fuerza entre los dos objetos, que se origina en los dos objetos, debe ser solo una función de su separación r y no de sus posiciones absolutas x ₁ y x ₂ ; de lo contrario, no habría simetría traslacional , y las leyes de la física tendrían que cambiar de un lugar a otro. Por lo tanto, la ecuación restada se puede escribir:

$${\ displaystyle \ mu {\ ddot {\ mathbf {r}}} = \ mathbf {F} _ {12} (\ mathbf {x} _ {1}, \ mathbf {x} _ {2}) = \ mathbf {F} (\ mathbf {r})}

dónde $${\ displaystyle \ mu}es la masa reducida

$${\ displaystyle \ mu = {\ frac {1} {{\ frac {1} {m_ {1}}} + {\ frac {1} {m_ {2}}}}} = {\ frac {m_ {1 } m_ {2}} {m_ {1} + m_ {2}}}.}

Resolver la ecuación para r ( t ) es la clave del problema de dos cuerpos; Los métodos generales de solución se describen a continuación.

Una vez que se han determinado R ( t ) yr ( t ), se pueden obtener las trayectorias originales

$${\ displaystyle \ mathbf {x} _ {1} (t) = \ mathbf {R} (t) + {\ frac {m_ {2}} {m_ {1} + m_ {2}}} \ mathbf {r } (t)}

$${\ displaystyle \ mathbf {x} _ {2} (t) = \ mathbf {R} (t) - {\ frac {m_ {1}} {m_ {1} + m_ {2}}} \ mathbf {r } (t)}

como puede verificarse sustituyendo las definiciones de R y r en los lados derechos de estas dos ecuaciones.

Movimiento de los dos cuerpos es planar [ editar ]

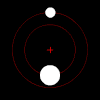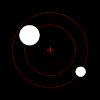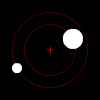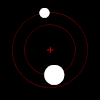
El movimiento de dos cuerpos uno con respecto al otro siempre se encuentra en un plano (en el centro del marco de masa ).

Prueba: definir el momento lineal p y el momento angular L del sistema, con respecto al centro de masa, mediante las ecuaciones

$${\ displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p} = \ mathbf {r} \ times \ mu {\ frac {d \ mathbf {r}} {dt}},}

donde μ es la masa reducida y r es la posición relativa r ₂ - r ₁ (con estas escritas tomando el centro de masa como el origen, y por lo tanto ambas paralelas a r ) la tasa de cambio del momento angular L es igual al par neto norte

$${\ displaystyle \ mathbf {N} = {\ frac {d \ mathbf {L}} {dt}} = {\ dot {\ mathbf {r}}} \ times \ mu {\ dot {\ mathbf {r}} } + \ mathbf {r} \ times \ mu {\ ddot {\ mathbf {r}}} \,}

y usando la propiedad del producto cruzado vectorial que v × w = 0 para cualquier vector v y w apuntando en la misma dirección,

$${\ displaystyle \ mathbf {N} \ = \ {\ frac {d \ mathbf {L}} {dt}} = \ mathbf {r} \ times \ mathbf {F} \,}

con F = μ d ² r / dt ² .

Introduciendo la suposición (verdadera de la mayoría de las fuerzas físicas, ya que obedecen la fuerte tercera ley del movimiento de Newton ) de que la fuerza entre dos partículas actúa a lo largo de la línea entre sus posiciones, se deduce que r × F  =   0 y el momento angular vector L es constante (conservado). Por lo tanto, el vector de desplazamiento r y su velocidad v son siempre en el plano perpendicular al vector constante L .

Energía del sistema de dos cuerpos [ editar ]

Si la fuerza F ( r ) es conservadora, entonces el sistema tiene una energía potencial U ( r ), por lo que la energíatotal se puede escribir como

$${\ displaystyle E _ {\ text {tot}} = {1 \ sobre 2} m_ {1} {\ dot {\ mathbf {x}}} _ {1} ^ {2} + {1 \ sobre 2} m_ { 2} {\ dot {\ mathbf {x}}} _ {2} ^ {2} + U (\ mathbf {r}) = {1 \ sobre 2} (m_ {1} + m_ {2}) {\ punto {\ mathbf {R}}} ^ {2} + {1 \ sobre 2} \ mu {\ dot {\ mathbf {r}}} ^ {2} + U (\ mathbf {r})}

En el centro del marco de masa, la energía cinética es la más baja y la energía total se convierte en

$${\ displaystyle E = {1 \ sobre 2} \ mu {\ dot {\ mathbf {r}}} ^ {2} + U (\ mathbf {r})}

Las coordenadas x ₁ y x ₂ se pueden expresar como

$${\ displaystyle \ mathbf {x} _ {1} = {\ frac {\ mu} {m_ {1}}} \ mathbf {r}}

$${\ displaystyle \ mathbf {x} _ {2} = - {\ frac {\ mu} {m_ {2}}} \ mathbf {r}}

y de manera similar, la energía E está relacionada con las energías E ₁ y E ₂ que contienen por separado la energía cinética de cada cuerpo:

{\ displaystyle {\ begin {alineado} E_ {1} & = {\ frac {\ mu} {m_ {1}}} E = {1 \ sobre 2} m_ {1} {\ dot {\ mathbf {x} }} _ {1} ^ {2} + {\ frac {\ mu} {m_ {1}}} U (\ mathbf {r}) \\ [4pt] E_ {2} & = {\ frac {\ mu } {m_ {2}}} E = {1 \ sobre 2} m_ {2} {\ dot {\ mathbf {x}}} _ {2} ^ {2} + {\ frac {\ mu} {m_ { 2}}} U (\ mathbf {r}) \\ [4pt] E _ {\ text {tot}} & = E_ {1} + E_ {2} \ end {alineado}}}

Fuerzas centrales [ editar ]

Artículo principal: Problema clásico de la fuerza central.

Para muchos problemas físicos, la fuerza F ( r ) es una fuerza central , es decir, es de la forma

$${\ displaystyle \ mathbf {F} (\ mathbf {r}) = F (r) {\ hat {\ mathbf {r}}}}

donde r = | r | y r̂ = r / r es el vector de la unidad correspondiente . Ahora tenemos:

$${\ displaystyle \ mu {\ ddot {\ mathbf {r}}} = {F} (r) {\ hat {\ mathbf {r}}} \,}

donde F ( r ) es negativo en el caso de una fuerza atractiva.

Una bola rebotadora capturada con un flash estroboscópico a 25 imágenes por segundo: ignorando la resistencia del aire , la raíz cuadrada de la relación entre la altura de un rebote y la del rebote anterior proporciona el coeficiente de restitución para el impacto bola / superficie.

El coeficiente de restitución ( COR ) es la relación entre la velocidad relativa final y la velocidad inicial entre dos objetos después de que colisionen. Normalmente oscila entre 0 y 1, donde 1 sería una colisión perfectamente elástica. Una colisión perfectamente inelástica tiene un coeficiente de 0, pero un valor de 0 no tiene que ser perfectamente inelástico. Se mide en la prueba de dureza de rebote de Leeb , expresada como 1000 veces el COR, pero solo es un COR válido para la prueba, no como un COR universal para el material que se está probando.

El valor es casi siempre menor a uno debido a que la energía cinética de traslación inicial se pierde debido a la energía cinética de rotación, la deformación plástica y el calor. Puede ser más de 1 si hay una ganancia de energía durante la colisión de una reacción química, una reducción de la energía de rotación u otra disminución de la energía interna que contribuye a la velocidad posterior a la colisión.

$${\ displaystyle {\ text {Coeficiente de restitución}} (e) = {\ frac {\ text {Velocidad relativa después de la colisión}} {\ text {Velocidad relativa antes de la colisión}}}}

El coeficiente está relacionado con la energía por $${\ displaystyle e = {\ sqrt {\ frac {KE _ {\ text {(después de la colisión)}}} {KE _ {\ text {(antes de la colisión)}}}}}

Las matemáticas fueron desarrolladas por Sir Isaac Newton en 1687. ^[1] También se conoce como ley experimental de Newton.

Más detalles [ editar ]

Línea de impacto : es la línea a lo largo de la cual e se define o, en ausencia de una fuerza de reacción tangencial entre las superficies en colisión, la fuerza del impacto se comparte a lo largo de esta línea entre los cuerpos. Durante el contacto físico entre cuerpos durante el impacto, su línea a lo largo de lo normal hasta un par de superficies en contacto con cuerpos en colisión. Por lo tanto, e se define como un parámetro unidimensional sin dimensiones.

Rango de valores para e - tratado como una constante [ editar ]

e es usualmente un número real positivo entre 0 y 1:

e = 0 : Esta es unacolisiónperfectamente inelástica . Esto significa que la energía cinética a lo largo de la normalidad común es 0. La energía cinética se convierte en calor o se trabaja para deformar los objetos.

0 < e <1 font=""> : Esta es una colisión inelástica del mundo real , en la que se disipa algo de energía cinética.

e = 1 : se trata de unacolisiónperfectamente elástica , en la que no se disipa energía cinética, y los objetos rebotan entre sí con la misma velocidad relativa con la que se acercaron.

e <0 font=""> : Un COR menor que cero representaría una colisión en la cual la velocidad de separación de los objetos tiene la misma dirección (signo) que la velocidad de cierre, lo que implica que los objetos pasaron uno a otro sin que se hayan aplicado completamente. Esto también puede considerarse como una transferencia incompleta de impulso. Un ejemplo de esto podría ser un objeto pequeño y denso que pasa a través de uno grande y menos denso, por ejemplo, una bala que pasa a través de un objetivo o una motocicleta que pasa por una casa rodante o una ola que atraviesa una presa.

e > 1 : Esto representaría una colisión en la que se libera energía, por ejemplo,las bolas de billar de nitrocelulosapueden explotar literalmente en el punto de impacto. Además, algunos artículos recientes han descrito colisiones superelásticas en las que se argumenta que el COR puede tomar un valor mayor que uno en un caso especial de colisiones oblicuas. ^{[2] [3] [4]} Estos fenómenos se deben al cambio de la trayectoria de rebote causado por la fricción. En tal colisión, la energía cinética aumenta de una manera en que la energía se libera en algún tipo de explosión. Es posible que$${\ displaystyle e = \ infty} Para una perfecta explosión de un sistema rígido.

Fase de deformación máxima : en cualquier colisión para 0 < e ≤ 1, existe una condición en la que, durante un breve momento a lo largo de la línea de impacto, los cuerpos en colisión tienen la misma velocidad cuando su condición de energía cinética se pierde en la fracción máxima como calor, sonido y luz con deformación. energía potencial. Para esta corta duración, esta colisión e = 0 y puede denominarse fase inelástica.

Objetos emparejados [ editar ]

El COR es una propiedad de un par de objetos en una colisión, no de un solo objeto. Si un objeto dado choca con dos objetos diferentes, cada colisión tendría su propio COR. Cuando se describe que un objeto tiene un coeficiente de restitución, como si fuera una propiedad intrínseca sin hacer referencia a un segundo objeto, se supone que está entre esferas idénticas o contra una pared perfectamente rígida.

Una pared perfectamente rígida no es posible, pero puede ser aproximada por un bloque de acero si se investiga el COR de esferas con un módulo de elasticidad mucho menor. De lo contrario, el COR aumentará y luego disminuirá según la velocidad de colisión de una manera más complicada. ^[5]

Relación con la conservación de la energía y el impulso [ editar ]

En una colisión unidimensional, los dos principios clave son: conservación de la energía (conservación de la energía cinética si la colisión es perfectamente elástica) y conservación del impulso (lineal). Una tercera ecuación se puede derivar ^[6] de estos dos, que es la ecuación de restitución como se indicó anteriormente. Al resolver problemas, se pueden usar dos de las tres ecuaciones. La ventaja de usar la ecuación de restitución es que a veces proporciona una manera más conveniente de abordar el problema.

Dejar $${\ displaystyle m_ {1}}, $${\ displaystyle m_ {2}}Ser la masa del objeto 1 y el objeto 2 respectivamente. Dejar$${\ displaystyle u_ {1}}, $${\ displaystyle u_ {2}}ser la velocidad inicial del objeto 1 y el objeto 2 respectivamente. Dejar$${\ displaystyle v_ {1}}, $${\ displaystyle v_ {2}} ser la velocidad final del objeto 1 y el objeto 2 respectivamente.

$${\ displaystyle {\ begin {cases} {\ frac {1} {2}} m_ {1} u_ {1} ^ {2} + {\ frac {1} {2}} m_ {2} u_ {2} ^ {2} = {\ frac {1} {2}} m_ {1} v_ {1} ^ {2} + {\ frac {1} {2}} m_ {2} v_ {2} ^ {2} \\ m_ {1} u_ {1} + m_ {2} u_ {2} = m_ {1} v_ {1} + m_ {2} v_ {2} \ end {cases}}}

De la primera ecuación,

$${\ displaystyle m_ {1} (u_ {1} ^ {2} -v_ {1} ^ {2}) = m_ {2} (v_ {2} ^ {2} -u_ {2} ^ {2}) }

$${\ displaystyle m_ {1} (u_ {1} + v_ {1}) (u_ {1} -v_ {1}) = m_ {2} (v_ {2} + u_ {2}) (v_ {2} -u_ {2})}

De la segunda ecuación,

$${\ displaystyle m_ {1} (u_ {1} -v_ {1}) = m_ {2} (v_ {2} -u_ {2})}

Después de la división,

$${\ displaystyle u_ {1} + v_ {1} = v_ {2} + u_ {2}}

$${\ displaystyle u_ {1} -u_ {2} = - (v_ {1} -v_ {2})}

$${\ displaystyle - {\ frac {v_ {1} -v_ {2}} {u_ {1} -u_ {2}}} = 1}

La ecuación anterior es la ecuación de restitución, y el coeficiente de restitución es 1, que es una colisión perfectamente elástica.

Equipamiento deportivo [ editar ]

Ver también: Bouncing ball § Reglamento deportivo.

El coeficiente de restitución entró en el vocabulario común, al menos entre los golfistas, cuando los fabricantes de palos de golf comenzaron a fabricar conductores de cara delgada con el llamado "efecto trampolín" que crea unidades de mayor distancia como resultado de la flexión y posterior liberación de Energía almacenada, impartiendo mayor impulso a la pelota. La USGA(El organismo de golf que gobierna en Estados Unidos) comenzó a probar los controladores de COR y ubicó el límite superior en 0.83. En abril de 2006 emitió un informe más detallado con cinco de las mejores pelotas de golf utilizadas por los golfistas profesionales. En este informe se destacan los hechos sobre pelotas de golf más allá del tema de COR. Debido a la naturaleza de los polímeros (plásticos hechos por el hombre) donde las tasas de tensión y tensión no son neutonales, como los fluidos, metales, etc. Debido a esto, la COR es una función de las velocidades de la cabeza del palo y disminuye a medida que aumenta la velocidad de la cabeza del palo. La USGA establece claramente que no se puede ganar mucho más allá de las 90 millas por hora de la velocidad del clubhead. En el informe, el rango de COR varía de 0.845 para 90 mph a tan solo 0.797 a 130 mph. El "efecto trampolín" mencionado anteriormente muestra esto claramente, ya que reduce la tasa de estrés de la colisión, o en otra palabra " raquetas de tenis ), "[f] o las condiciones de referencia, el coeficiente de restitución utilizado es de 0.85 para todas las raquetas, eliminando las variables de tensión de las cuerdas y la rigidez del cuadro que podrían sumarse o restar del coeficiente de restitución". ^[7]

La Federación Internacional de Tenis de Mesa especifica que la pelota rebotará entre 24 y 26 cm cuando se la deje caer desde una altura de 30,5 cm a un bloque de acero estándar con un COR de 0,89 a 0,92. ^[8] Para un piso de linóleo duro con concreto debajo, una pelota de baloncesto de cuero tiene un COR alrededor de 0.81–0.85. ^[9]

Ecuaciones [ editar ]

En el caso de una colisión unidimensional que involucra dos objetos, el objeto A y el objeto B, el coeficiente de restitución viene dado por:

$${\ displaystyle C_ {R} = {\ frac {v _ {\ text {b}} - v _ {\ text {a}}} {u _ {\ text {a}} - u _ {\ text {b}}}} }, dónde:

$${\ displaystyle v _ {\ text {a}}} es la velocidad final del objeto A después del impacto

$${\ displaystyle v _ {\ text {b}}} es la velocidad final del objeto B después del impacto

$${\ displaystyle u _ {\ text {a}}} es la velocidad inicial del objeto A antes del impacto

$${\ displaystyle u _ {\ text {b}}} es la velocidad inicial del objeto B antes del impacto

Aunque $${\ displaystyle C_ {R}}no depende explícitamente de las masas de los objetos, es importante tener en cuenta que las velocidades finales dependen de la masa. Para colisiones bidimensionales y tridimensionales de cuerpos rígidos, las velocidades utilizadas son los componentes perpendiculares a la línea / plano tangente en el punto de contacto, es decir, a lo largo de la línea de impacto.

Para un objeto que rebota en un objetivo estacionario, $${\ displaystyle C_ {R}} se define como la relación entre la velocidad del objeto después del impacto y la de antes del impacto:

$${\ displaystyle C_ {R} = {\ frac {v} {u}}}, dónde

$${\ displaystyle v} Es la velocidad del objeto después del impacto.

$${\ displaystyle u} Es la velocidad del objeto antes del impacto.

En un caso donde las fuerzas de fricción pueden ser desatendidas y el objeto se deja caer desde una superficie horizontal, esto equivale a:

$${\ displaystyle C_ {R} = {\ sqrt {\ frac {h} {H}}}}, dónde

$${\ displaystyle h} es la altura de rebote

$${\ displaystyle H} es la altura de caída

El coeficiente de restitución se puede considerar como una medida de la medida en que se conserva la energía mecánica cuando un objeto rebota en una superficie. En el caso de que un objeto rebote en un objetivo estacionario, el cambio en la energía potencial gravitatoria, PE , durante el curso del impacto es esencialmente cero; así,$${\ displaystyle C_ {R}}es una comparación entre la energía cinética, KE , del objeto inmediatamente antes del impacto y la que aparece inmediatamente después del impacto:

$${\ displaystyle C_ {R} = {\ sqrt {\ frac {KE _ {\ text {(después del impacto)}}} {KE _ {\ text {(antes del impacto)}}}}} = {\ sqrt {\ frac { {\ frac {1} {2}} mv ^ {2}} {{\ frac {1} {2}} mu ^ {2}}}} = {\ sqrt {\ frac {v ^ {2}} { u ^ {2}}}} = {\ frac {v} {u}}}

En los casos en que se pueden ignorar las fuerzas de fricción (casi todos los laboratorios de estudiantes sobre este tema ^[10] ) y el objeto se deja caer desde una superficie horizontal, lo anterior es equivalente a una comparación entre el PE del objeto en la altura de caída Con eso a la altura de rebote. En este caso, el cambio en KE es cero (el objeto está esencialmente en reposo durante el curso del impacto y también está en reposo en el vértice del rebote); así:

$${\ displaystyle C_ {R} = {\ sqrt {\ frac {PE _ {\ text {(a altura de rebote)}}} {PE _ {\ text {(a altura de caída)}}}}} = {\ sqrt {\ frac {mgh} {mgH}}} = {\ sqrt {\ frac {h} {H}}}}

Velocidades después del impacto [ editar ]

Las ecuaciones para las colisiones entre partículas elásticas se pueden modificar para usar el COR, por lo que también se pueden aplicar a las colisiones inelásticas y a todas las posibilidades intermedias.

$${\ displaystyle v_ {a} = {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} + m _ {\ text {b}} C_ {R} (u _ {\ text {b}} - u _ {\ text {a}})} {m _ {\ text {a}} + m _ {\ text {b}}}}}

y

$${\ displaystyle v _ {\ text {b}} = {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} + m _ {\ text {a}} C_ {R} (u _ {\ text {a}} - u _ {\ text {b}})} {m _ {\ text {a}} + m _ {\ text {b}} }}}

dónde

$${\ displaystyle v _ {\ text {a}}} Es la velocidad final del primer objeto después del impacto.

$${\ displaystyle v _ {\ text {b}}} Es la velocidad final del segundo objeto después del impacto.

$${\ displaystyle u _ {\ text {a}}} Es la velocidad inicial del primer objeto antes del impacto.

$${\ displaystyle u _ {\ text {b}}} es la velocidad inicial del segundo objeto antes del impacto

$${\ displaystyle m _ {\ text {a}}} es la masa del primer objeto

$${\ displaystyle m _ {\ text {b}}} es la masa del segundo objeto

Derivación [ editar ]

Las ecuaciones anteriores se pueden derivar de la solución analítica al sistema de ecuaciones formado por la definición de la COR y la ley de la conservación del momento (que se aplica a todas las colisiones). Usando la notación de arriba donde$${\ displaystyle u} representa la velocidad antes de la colisión y $${\ displaystyle v} despues, cede:

{\ displaystyle {\ begin {alineado} & m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} = m _ {\ text {a} } v _ {\ text {a}} + m _ {\ text {b}} v _ {\ text {b}} \\ & C_ {R} = {\ frac {v _ {\ text {b}} - v _ {\ text {a}}} {u _ {\ text {a}} - u _ {\ text {b}}}} \\\ end {alineado}}}

Resolviendo la ecuación de conservación del momento para $${\ displaystyle v _ {\ text {a}}} y la definición del coeficiente de restitución para $${\ displaystyle v _ {\ text {b}}} rendimientos

{\ displaystyle {\ begin {alineado} & {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} - m_ { \ text {b}} v _ {\ text {b}}} {m _ {\ text {a}}}} = v _ {\ text {a}} \\ & v _ {\ text {b}} = C_ {R} (u _ {\ text {a}} - u _ {\ text {b}}) + v _ {\ text {a}} \\\ final {alineado}}}

A continuación, la sustitución en la primera ecuación de $${\ displaystyle v _ {\ text {b}}} y luego resolviendo para $${\ displaystyle v _ {\ text {a}}} da:

{\ displaystyle {\ begin {alineado} & {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} - m_ { \ text {b}} C_ {R} (u _ {\ text {a}} - u _ {\ text {b}}) - m _ {\ text {b}} v _ {\ text {a}}} {m_ { \ text {a}}}} = v _ {\ text {a}} \\ & \\ & {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b }} u _ {\ text {b}} + m _ {\ text {b}} C_ {R} (u _ {\ text {b}} - u _ {\ text {a}})} {m _ {\ text {a }}}} = v _ {\ text {a}} \ left [1 + {\ frac {m _ {\ text {b}}} {m _ {\ text {a}}}} \ right] \\ & \\ & {\ frac {m _ {\ text {a}} u _ {\ text {a}} + m _ {\ text {b}} u _ {\ text {b}} + m _ {\ text {b}} C_ {R } (u _ {\ text {b}} - u _ {\ text {a}})} {m _ {\ text {a}} + m _ {\ text {b}}}} = v _ {\ text {a}} \\\ fin {alineado}}}

Una derivación similar arroja la fórmula para $${\ displaystyle v _ {\ text {b}}}.

Variación de COR debido a la forma del objeto y colisiones descentradas [ editar ]

Cuando los objetos en colisión no tienen una dirección de movimiento que esté en línea con sus centros de gravedad y punto de impacto, o si las superficies de contacto en ese punto no son perpendiculares a esa línea, habrá energía disponible para el poste. -La diferencia de velocidad de colisión se perderá por la rotación y la fricción. Las pérdidas de energía a la vibración y el sonido resultante suelen ser despreciables.

Chocan diferentes materiales y medición práctica [ editar ]

Cuando un objeto blando golpea un objeto más duro, la mayor parte de la energía disponible para la velocidad posterior a la colisión se almacenará en el objeto blando. El COR dependerá de cuán eficiente sea el objeto blando para almacenar la energía en compresión sin perderla por el calor y la deformación plástica. Una bola de goma rebotará mejor en concreto que una bola de vidrio, pero el COR del vidrio sobre vidrio es mucho más alto que el de goma sobre caucho porque parte de la energía del caucho se pierde en calor cuando se comprime. Cuando una bola de goma choca con una bola de cristal, el COR dependerá completamente de la goma. Por esta razón, la mejor manera de determinar el COR de un material cuando no hay material idéntico para la colisión es usar un material mucho más duro.

Dado que no hay un material perfectamente rígido, los materiales duros como los metales y las cerámicas tienen su COR determinado teóricamente considerando la colisión entre esferas idénticas. En la práctica, se puede emplear una cuna de Newton de dos bolas , pero tal configuración no es propicia para analizar muestras rápidamente.

La prueba de dureza de rebote de Leeb es la única prueba comúnmente disponible relacionada con la determinación del COR. Utiliza una punta de carburo de tungsteno, una de las sustancias más duras disponibles, colocada sobre muestras de prueba desde una altura específica. Pero la forma de la punta, la velocidad de impacto y el carburo de tungsteno son variables que afectan el resultado que se expresa en términos de 1000 * COR. No da un COR objetivo para el material que es independiente de la prueba.

Predicción a partir de propiedades del material [ editar ]

El COR no es una propiedad del material porque cambia con la forma del material y las características específicas de la colisión, pero puede predecirse a partir de las propiedades del material y la velocidad de impacto cuando se simplifican las características específicas de la colisión. Para evitar las complicaciones de las pérdidas por rotación y fricción, podemos considerar el caso ideal de un par idéntico de objetos esféricos, que colisionan de modo que sus centros de masa y velocidad relativa estén todos en línea.

Se supone que muchos materiales como los metales y la cerámica (pero no los cauchos y los plásticos) son perfectamente elásticos cuando no se alcanza su resistencia en el impacto. La energía de impacto se almacena teóricamente solo en el efecto de resorte de la compresión elástica y los resultados en e= 1. Pero esto se aplica solo a velocidades inferiores a aproximadamente 0,1 m / sa 1 m / s. El rango elástico se puede superar a velocidades más altas porque toda la energía cinética se concentra en el punto de impacto. Específicamente, el límite elástico generalmente se excede en parte del área de contacto, perdiendo energía a la deformación plástica al no permanecer en la región elástica. Para tener en cuenta esto, lo siguiente estima el COR estimando el porcentaje de la energía de impacto inicial que no se perdió por la deformación plástica. Aproximadamente, divide la facilidad con la que un volumen de material puede almacenar energía en compresión ($${\ displaystyle 1 / {\ text {módulo elástico}}}) por lo bien que puede mantenerse en el rango elástico ($${\ displaystyle 1 / {\ text {fuerza de rendimiento}}}):

$${\ displaystyle \% {\ text {energía de impacto disponible para restitución}} \ propto {\ frac {\ text {fuerza de rendimiento}} {\ text {módulo elástico}}}}

Para una densidad y velocidad de material dada, esto resulta en:

$${\ displaystyle {\ text {coeficiente de restitución}} \ propto {\ sqrt {\ frac {\ text {fuerza de rendimiento}} {\ text {módulo elástico}}}}}

Una resistencia de alto rendimiento permite que más del "volumen de contacto" del material permanezca en la región elástica a energías más altas. Un módulo de elasticidad más bajo permite que se desarrolle un área de contacto más grande durante el impacto, por lo que la energía se distribuye a un volumen más grande debajo de la superficie en el punto de contacto. Esto ayuda a evitar que se exceda la resistencia del rendimiento.

Un desarrollo teórico más preciso ^[11] muestra que la velocidad y la densidad del material también son importantes a la hora de predecir el COR a velocidades moderadas más rápidas que la colisión elástica (mayor que 0,1 m / s para metales) y más lentas que una deformación plástica permanente grande (menos de 100 m / s). Una velocidad más baja aumenta el coeficiente al necesitar menos energía para ser absorbida. Una densidad más baja también significa que se necesita menos energía inicial para ser absorbida. Se usa la densidad en lugar de la masa porque el volumen de la esfera se cancela con el volumen del volumen afectado en el área de contacto. De esta manera, el radio de la esfera no afecta el coeficiente. Un par de esferas en colisión de diferentes tamaños pero del mismo material tienen el mismo coeficiente que el de abajo, pero multiplicado por$${\ displaystyle \ left ({\ frac {R_ {1}} {R_ {2}}} \ right) ^ {\ frac {3} {8}}}

Combinando estas cuatro variables, se puede hacer una estimación teórica del coeficiente de restitución cuando una pelota cae sobre una superficie del mismo material. ^[12]

• e = coeficiente de restitución
• S _y = elasticidad dinámica ("límite elástico" dinámico)
• E ′ = módulo elástico efectivo
• ρ = densidad
• v = velocidad en el impacto
• μ = relación de Poisson

$${\ displaystyle e = 3.1 \ left ({\ frac {S _ {\ text {y}}} {1}} \ right) ^ {\ frac {5} {8}} \ left ({\ frac {1} { E '}} \ right) ^ {\ frac {1} {2}} \ left ({\ frac {1} {v}} \ right) ^ {\ frac {1} {4}} \ left ({\ frac {1} {\ rho}} \ right) ^ {\ frac {1} {8}}}

$${\ displaystyle E '= {\ frac {E} {1- \ mu ^ {2}}}}

Esta ecuación sobreestima el COR real. Para los metales, se aplica cuando v está aproximadamente entre 0.1 m / sy 100 m / sy en general cuando:

{\ displaystyle 0.001 <{\ frac {\ rho v ^ {2}} {S _ {\ text {y}}}} <0 .1="" font="">

A velocidades más lentas, el COR es más alto de lo que predice la ecuación anterior, alcanzando teóricamente e = 1 cuando la fracción anterior es menor que $${\ displaystyle 10 ^ {- 6}}Sra. Da el siguiente coeficiente teórico de restitución para esferas sólidas caídas 1 metro ( v = 4.5 m / s). Los valores superiores a 1 indican que la ecuación tiene errores. Se utilizó la fuerza de rendimiento en lugar de la fuerza de rendimiento dinámico.

Metales y Cerámica:	COR predicho, e
silicio	1.79
Alúmina	0.45 a 1.63
Nitrido de silicona	0.38 a 1.63
carburo de silicio	0.47 a 1.31
metal amorfo mas alto	1.27
carburo de tungsteno	0.73 a 1.13
acero inoxidable	0.63 a 0.93
aleaciones de magnesio	0.5 a 0.89
aleación de titanio grado 5	0.84
aleación de aluminio 7075-T6	0.75
vidrio (soda-lima)	0.69
vidrio (borosilicato)	0.66
aleaciones de níquel	0.15 a 0.70
aleaciones de zinc	0.21 a 0.62
hierro fundido	0.3 a 0.6
Aleaciones de cobre	0.15 a 0.55
titanio grado 2	0.46
tungsteno	0.37
Aleaciones de aluminio 3003 6061, 7075-0.	0.35
zinc	0.21
níquel	0.15
cobre	0.15
aluminio	0.1
dirigir	0.08

El COR para plásticos y cauchos es mayor que sus valores reales porque no se comportan de manera ideal elástica como metales, vidrios y cerámicas debido al calentamiento durante la compresión. Así que lo siguiente es solo una guía para la clasificación de polímeros.

Polímeros (sobrestimados en comparación con metales y cerámicas):

• Polibutadieno (cáscara de pelotas de golf) 11.8
• caucho butilo 6.24
• EVA 4.85
• elastómeros de silicona 2.80
• policarbonato 1.46
• nylon 1.28
• polietileno 1.24
• Teflon 1.21
• polipropileno 1.14
• ABS 1.12
• acrilico 1.06
• PET 0.95
• poliestireno 0.87
• PVC 0.86

Para los metales, el rango de velocidades a los que puede aplicarse esta teoría es de aproximadamente 0,1 a 5 m / s, lo que representa una caída de 0,5 mm a 1,25 metros (página 366 ^[13] ).