QUÍMICA FÍSICA

El potencial de Donnan aparece como resultado del equilibrio de Donnan , llamado así por Frederick G. Donnan, que se refiere a la distribución de las especies de iones entre dos soluciones iónicas separadas por una membrana o un límite semipermeable . La capa límite mantiene una distribución desigual de la concentración de soluto iónico al actuar como una barrera selectiva para la difusión iónica . Algunas especies de iones pueden pasar a través de la barrera, mientras que otras pueden no pasar. Las soluciones pueden ser geles o coloides , así como líquidos iónicos, y como tal, el límite de fase entre geles o un gel y un líquido también puede actuar como una barrera selectiva.El potencial eléctrico que surge entre dos soluciones se denomina potencial de Donnan.

El equilibrio de Donnan es prominente en el modelo trifásico para cartílago articular propuesto por Mow y Ratcliffe, así como en celdas de combustible electroquímicas y diálisis .

El efecto Donnan es una presión osmótica adicional atribuible a los cationes (Na ⁺ y K ⁺ ) unidos a las proteínas plasmáticas disueltas.

capa doble es la superficie donde dos fases diferentes de la materia están en contacto. Las capas dobles biológicas son muy parecidas a sus contrapartes interfaciales , pero con varias distinciones notables.

La superficie de las células biológicas contiene muchos tipos diferentes de grupos químicos , cada uno con una constante de disociación diferente , lo que hace que tengan cargas eléctricas variables a un pH fisiológico . Esto indica que las biosuperficies son químicamente heterogéneas . Esta característica bioespecífica es típica de todas las biosuperficies, incluidas las proteínas , las macromoléculas y las células biológicas .

En ciertos organismos, las células se cubren con la capa de glicocalix , que se puede modelar como una capa de polielectrolito con una carga eléctrica de distribución de volumen. ^{[ aclaración necesaria ]} Esto significa que la noción de carga superficial se encuentra en ciertas superficies planas. Esto no se aplica; en cambio, la superficie de la celda es una capa de polielectrolito de espesor finito con una carga de volumen. En el equilibrio , la relación entre estas capas de polielectrolito y un volumen fluido se denomina equilibrio de Donnan . La carga de volumen de polielectrolito crea un potencial eléctrico equilibrado conocido como el potencial de Donnan .^[1] Parte del potencial de Donnan se encuentra dentro de la capa de polielectrolito, mientras que la otra parte está asociada con la capa doble externa ubicada en el medio de dispersión .

En otra característica, las células no están en equilibrio con el volumen de fluido. Existe un intercambio iónicoconstante entre las células vivas y un fluido. En consecuencia, existe una diferencia en los potenciales eléctricos entre el interior de la celda y un volumen de fluido, conocido como el potencial transmembrana . ^[2] Este potencial de no equilibrio afecta la estructura de la doble capa.

Dispersión de luz dinámica hipotética de dos muestras: partículas más grandes en la parte superior y partículas más pequeñas en la parte inferior

La dispersión dinámica de la luz ( DLS ) es una técnica en física que se puede utilizar para determinar el perfil de distribución de tamaño de partículas pequeñas en suspensión o polímeros en solución . ^[1] En el ámbito de la DLS, las fluctuaciones temporales se analizan generalmente mediante la función de intensidad o autocorrelación de fotones (también conocida como espectroscopia de correlación de fotones o dispersión de luz cuasi elástica). En el análisis del dominio del tiempo, la función de autocorrelación (ACF) generalmente decae a partir del tiempo de retardo cero, y una dinámica más rápida debido a partículas más pequeñas conduce a una descorrelación más rápida de la traza de intensidad dispersada. Se ha demostrado que la intensidad ACF es la transformación de Fourier del espectro de potencia y, por lo tanto, las mediciones de DLS se pueden realizar igualmente en el dominio espectral. ^{[2] [3] El} DLS también se puede usar para probar el comportamiento de fluidos complejos como las soluciones de polímeros concentrados.

Configuración [ editar ]

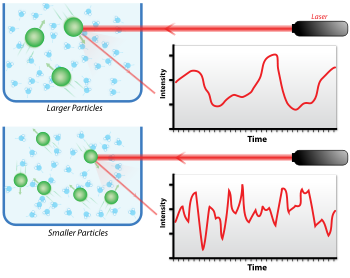
Una fuente de luz monocromática, generalmente un láser, se dispara a través de un polarizador y en una muestra. Luego, la luz dispersada atraviesa un segundo polarizador, donde lo recoge un fotomultiplicador y la imagen resultante se proyecta en una pantalla. Esto se conoce como un patrón de moteado (Figura 1). ^[4]

Figura 1. Patrón de moteado típico.

Todas las moléculas en la solución están siendo golpeadas con la luz y todas las moléculas difractan la luz en todas direcciones. La luz difractada de todas las moléculas puede interferir constructivamente (regiones de luz) o destructivamente (regiones oscuras). Este proceso se repite a intervalos de tiempo cortos y el conjunto resultante de patrones de moteado se analiza mediante un autocorrelador que compara la intensidad de la luz en cada punto a lo largo del tiempo. Los polarizadores se pueden configurar en dos configuraciones geométricas. Una es una geometría vertical / vertical (VV), donde el segundo polarizador permite que la luz pase por la misma dirección que el polarizador primario. En geometría vertical / horizontal (VH), el segundo polarizador permite que la luz no se encuentre en la misma dirección que la luz incidente.

Descripción [ editar ]

Cuando la luz incide en partículas pequeñas, la luz se dispersa en todas las direcciones ( dispersión de Rayleigh) siempre que las partículas sean pequeñas en comparación con la longitud de onda (por debajo de 250 nm ). Incluso si la fuente de luz es un láser , y por lo tanto es monocromática y coherente , la intensidad de la dispersión fluctúa con el tiempo. Esta fluctuación se debe a pequeñas moléculas en soluciones que experimentan un movimiento browniano.Y así, la distancia entre los dispersores en la solución cambia constantemente con el tiempo. Esta luz dispersada sufre una interferencia constructiva o destructiva por parte de las partículas circundantes, y dentro de esta fluctuación de intensidad, la información está contenida sobre la escala de tiempo del movimiento de los dispersadores. La preparación de la muestra, ya sea por filtración o centrifugación, es fundamental para eliminar el polvo y los artefactos de la solución.

La información dinámica de las partículas se deriva de una autocorrelación de la traza de intensidad registrada durante el experimento. La curva de autocorrelación de segundo orden se genera a partir de la traza de intensidad de la siguiente manera:

$${\ displaystyle g ^ {2} (q; \ tau) = {\ frac {\ langle I (t) I (t + \ tau) \ rangle} {\ langle I (t) \ rangle ^ {2}}}}

donde g ² ( q ; τ ) es la función de autocorrelación en un vector de onda particular, q , y el tiempo de retardo, τ , e I es la intensidad. Los corchetes angulares <> denotan el operador de valor esperado , que en algunos textos se denota con una E mayúscula .

A corto plazo, la correlación es alta porque las partículas no tienen la posibilidad de moverse en gran medida desde el estado inicial en el que se encontraban. Las dos señales permanecen esencialmente sin cambios cuando se comparan después de un intervalo de tiempo muy corto. A medida que los retrasos se hacen más largos, la correlación decae exponencialmente, lo que significa que, después de que haya transcurrido un largo período de tiempo, no existe una correlación entre la intensidad dispersada de los estados inicial y final. Esta caída exponencial está relacionada con el movimiento de las partículas, específicamente con el coeficiente de difusión. Para ajustar la descomposición (es decir, la función de autocorrelación), se utilizan métodos numéricos, basados ​​en cálculos de distribuciones supuestas. Si la muestra es monodispersa.entonces el decaimiento es simplemente un solo exponencial. La ecuación de Siegert relaciona la función de autocorrelación de segundo orden con la función de autocorrelación de primer orden g ¹ ( q ; τ ) de la siguiente manera:

$${\ displaystyle g ^ {2} (q; \ tau) = 1 + \ beta \ left [g ^ {1} (q; \ tau) \ right] ^ {2}}

donde el parámetro β es un factor de corrección que depende de la geometría y la alineación del rayo láser en la configuración de dispersión de la luz. Es aproximadamente igual a la inversa del número de motas (ver Patrón de motas ) desde el cual se recoge la luz. Un foco más pequeño del rayo láser produce un patrón de moteado más grueso, un menor número de motas en el detector y, por lo tanto, una autocorrelación de segundo orden más grande.

El uso más importante de la función de autocorrelación es su uso para la determinación del tamaño.

Dispersión múltiple [ editar ]

La dispersión dinámica de la luz proporciona información sobre las propiedades dinámicas de los materiales blandos mediante la medición de eventos de dispersión única, lo que significa que cada fotón detectado ha sido dispersado por la muestra exactamente una vez. Sin embargo, la aplicación a muchos sistemas de relevancia científica e industrial ha sido limitada debido a la dispersión múltiple frecuentemente encontrada, en donde la muestra dispersa los fotones varias veces antes de ser detectada. La interpretación precisa se vuelve extremadamente difícil para los sistemas con contribuciones no insignificantes de la dispersión múltiple. Especialmente para partículas más grandes y aquellas con alto índice de contraste de refracción, esto limita la técnica a concentraciones de partículas muy bajas, y una gran variedad de sistemas, por lo tanto, están excluidos de las investigaciones con dispersión dinámica de la luz. Sin embargo, como lo muestra Schaetzel,^[5] es posible suprimir la dispersión múltiple en experimentos de dispersión dinámica de la luz a través de un enfoque de correlación cruzada. La idea general es aislar la luz dispersada individualmente y suprimir las contribuciones no deseadas de la dispersión múltiple en un experimento de dispersión dinámica de la luz. Se han desarrollado y aplicado diferentes implementaciones de dispersión de luz de correlación cruzada. Actualmente, el esquema más utilizado es el denominado método de dispersión de luz dinámico en 3D. ^[6] [7] El mismo método también se puede utilizar para corregirdatos de dispersión de luz estática para múltiples contribuciones de dispersión. ^[8]Alternativamente, en el límite de la dispersión múltiple fuerte, una variante de la dispersión dinámica de la luz llamada espectroscopía de onda difusa puede ser aplicado.

Análisis de datos [ editar ]

Introducción [ editar ]

Una vez que se han generado los datos de autocorrelación, se pueden emplear diferentes enfoques matemáticos para determinar la "información" a partir de ella. El análisis de la dispersión se facilita cuando las partículas no interactúan a través de colisiones o fuerzas electrostáticas entre los iones. Las colisiones partícula-partícula se pueden suprimir por dilución, y los efectos de carga se reducen mediante el uso de sales para colapsar la doble capa eléctrica .

El enfoque más simple es tratar la función de autocorrelación de primer orden como una sola disminución exponencial. Esto es apropiado para una población monodispersa.

$${\ displaystyle \ g ^ {1} (q; \ tau) = \ exp (- \ Gamma \ tau) \,}

donde Γ es la tasa de descomposición. El coeficiente de difusión de la traducción D _t puede derivarse en un ángulo único o en un rango de ángulos dependiendo del vector de onda q .

$${\ displaystyle \ \ Gamma = q ^ {2} D_ {t} \,}

con

$${\ displaystyle \ q = {\ frac {4 \ pi n_ {0}} {\ lambda}} \ sin \ left ({\ frac {\ theta} {2}} \ right)}

donde λ es la longitud de onda del láser incidente, n ₀ es el índice de refracción de la muestra y θ es el ángulo en el que se encuentra el detector con respecto a la celda de la muestra.

Dependiendo de la anisotropía y la polidispersidad del sistema, una gráfica resultante de (Γ / q ² ) vs. q ² puede o no mostrar una dependencia angular. Las partículas esféricas pequeñas no mostrarán dependencia angular, por lo tanto no habrá anisotropía. Una gráfica de (Γ / q ² ) vs. q ² resultará en una línea horizontal. Las partículas con una forma que no sea una esfera mostrarán una anisotropía y, por lo tanto, una dependencia angular al trazar (Γ / q ² ) vs. q ² . ^[9] La intercepción será en todo caso la D_t . Por lo tanto, existe un ángulo óptimo de detección θ para cada tamaño de partícula. Un análisis de alta calidad siempre debe realizarse en varios ángulos de dispersión (DLS de triángulos). Esto se vuelve aún más importante en una muestra polidispersa con una distribución de tamaño de partícula desconocida. En ciertos ángulos, la intensidad de dispersión de algunas partículas abrumará completamente la débil señal de dispersión de otras partículas, lo que las hace invisibles para el análisis de datos en este ángulo. Los instrumentos DLS que solo funcionan en un ángulo fijo solo pueden ofrecer buenos resultados para algunas partículas. Por lo tanto, la precisión indicada de un instrumento DLS con un solo ángulo de detección solo es cierta para ciertas partículas.

D _t se usa a menudo para calcular el radio hidrodinámico de una esfera a través de la ecuación de Stokes-Einstein . Es importante tener en cuenta que el tamaño determinado por la dispersión dinámica de la luz es el tamaño de una esfera que se mueve de la misma manera que el dispersor. Entonces, por ejemplo, si el dispersor es un polímero de bobina al azar, el tamaño determinado no es el mismo que el radio de giro determinado por la dispersión de la luz estática . También es útil señalar que el tamaño obtenido incluirá cualquier otra molécula o molécula de disolvente que se mueva con la partícula. Así, por ejemplo, el oro coloidal.con una capa de surfactante aparecerá más grande por dispersión de luz dinámica (que incluye la capa de surfactante) que por microscopía electrónica de transmisión (que no "ve" la capa debido a un contraste pobre).

En la mayoría de los casos, las muestras son polidispersas. Por lo tanto, la función de autocorrelación es una suma de los decaimientos exponenciales correspondientes a cada una de las especies en la población.

$${\ displaystyle g ^ {1} (q; \ tau) = \ sum _ {i = 1} ^ {n} G_ {i} (\ Gamma _ {i}) \ exp (- \ Gamma _ {i} \ tau) = \ int G (\ Gamma) \ exp (- \ Gamma \ tau) \, d \ Gamma.}

Es tentador obtener datos para g ¹ ( q ; τ ) e intentar invertir lo anterior para extraer G (Γ) . Dado que G (Γ) es proporcional a la dispersión relativa de cada especie, contiene información sobre la distribución de tamaños. Sin embargo, esto se conoce como un problema mal planteado . Los métodos descritos a continuación (y otros) se han desarrollado para extraer la mayor cantidad de información útil posible de una función de autocorrelación.

Metodo cumulant [ editar ]

Uno de los métodos más comunes es el método de acumulación , ^[10] [11] del cual, además de la suma de los exponenciales anteriores, se puede obtener más información sobre la varianza del sistema de la siguiente manera:

$${\ displaystyle \ g ^ {1} (q; \ tau) = \ exp \ left (- {\ bar {\ Gamma}} \ left (\ tau - {\ frac {\ mu _ {2}} {2! }} \ tau ^ {2} + {\ frac {\ mu _ {3}} {3!}} \ tau ^ {3} + \ cdots \ right) \ right)}

donde Γ es la tasa de disminución promedio y μ ₂ / Γ ² es el índice de polidispersidad de segundo orden (o una indicación de la varianza). También se puede derivar un índice de polidispersidad de tercer orden, pero esto es necesario solo si las partículas del sistema son altamente polidispersas. El coeficiente de difusión traduccional promediado en _z D _z puede derivarse en un ángulo único o en un rango de ángulos dependiendo del vector de onda q .

$${\ displaystyle \ {\ bar {\ Gamma}} = q ^ {2} D_ {z} \,}

Se debe tener en cuenta que el método de acumulación es válido para τ pequeño y G ( Γ ) suficientemente estrecho . ^[12] Rara vez se deben usar parámetros más allá de µ ₃ , porque el exceso de datos con muchos parámetros en una expansión de la serie Power hará que todos los parámetros incluyan$${\ displaystyle \ scriptstyle {\ bar {\ Gamma}}}y µ ₂ , menos precisos. ^[13] El método experimental se ve mucho menos afectado por el ruido experimental que los métodos a continuación.

Algoritmo CONTIN [ editar ]

Un método alternativo para analizar la función de autocorrelación se puede lograr a través de una transformada inversa de Laplace conocida como CONTIN desarrollada por Steven Provencher. ^[14] [15] El análisis CONTIN es ideal para sistemas heterodispersos , polidispersos y multimodales que no pueden resolverse con el método de acumulación. La resolución para separar dos poblaciones de partículas diferentes es aproximadamente un factor de cinco o mayor y la diferencia en las intensidades relativas entre dos poblaciones diferentes debe ser inferior a 1:10 ⁻⁵ .

Método de máxima entropía [ editar ]

El método de entropía máxima es un método de análisis que tiene un gran potencial de desarrollo. El método también se utiliza para la cuantificación de datos de velocidad de sedimentación de ultracentrifugación analítica . El método de máxima entropía implica una serie de pasos iterativos para minimizar la desviación de los datos ajustados de los datos experimentales y, posteriormente, reducir la χ ² de los datos ajustados.

Dispersión de partículas no esféricas [ editar ]

Si la partícula en cuestión no es esférica, también se debe considerar el movimiento de rotación, ya que la dispersión de la luz será diferente según la orientación. Según Pecora, el movimiento browniano rotacional afectará la dispersión cuando una partícula cumpla dos condiciones; deben ser tanto anisotrópicos ópticamente como geométricamente. ^[16] Las moléculas en forma de barra cumplen estos requisitos, por lo que se debe considerar un coeficiente de difusión rotacional además de un coeficiente de difusión traslacional. En su forma más sucinta, la ecuación aparece como

$${\ displaystyle {\ frac {A} {B}} = {\ frac {5} {4}} {\ frac {4 \ mathrm {M} _ {p} +2 \ mathrm {N} \ mathrm {M} _ {l} \ mathrm {M} _ {p} + \ mathrm {M} _ {l}} {\ mathrm {M} _ {p} - \ mathrm {N} + \ mathrm {M} _ {l} }}}

Donde A / B es la relación de los dos modos de relajación (traslacional y rotacional), M _p contiene información sobre el eje perpendicular al eje central de la partícula y M _l contiene información sobre el eje paralelo al eje central.

En 2007, Peter R. Lang y su equipo decidieron usar la dispersión dinámica de la luz para determinar la longitud de las partículas y la relación de aspecto de los nanorods de oro cortos. ^[17] Eligieron este método debido a que no destruye la muestra y tiene una configuración relativamente fácil. Ambos estados de relajación se observaron en la geometría VV y los coeficientes de difusión de ambos movimientos se utilizaron para calcular las relaciones de aspecto de las nanopartículas de oro.

Aplicaciones [ editar ]

DLS se utiliza para caracterizar el tamaño de varias partículas, incluyendo proteínas, polímeros, micelas, vesículas ^[18] , carbohidratos, nanopartículas, células biológicas ^[19] y geles ^[20] . Si el sistema no se dispersa en tamaño, se puede determinar el diámetro medio efectivo de las partículas. Esta medida depende del tamaño del núcleo de la partícula, el tamaño de las estructuras de la superficie, la concentración de la partícula y el tipo de iones en el medio.

Dado que DLS mide esencialmente las fluctuaciones en la intensidad de la luz dispersada debido a las partículas de difusión, se puede determinar el coeficiente de difusión de las partículas. El software DLS de instrumentos comerciales normalmente muestra la población de partículas en diferentes diámetros. Si el sistema es monodisperso, solo debería haber una población, mientras que un sistema polidisperso mostraría múltiples poblaciones de partículas. Si hay más de un tamaño de población presente en una muestra, entonces se debe aplicar el análisis CONTIN para los instrumentos de espectroscopia de correlación de fotones, o el método de espectro de potencia debe aplicarse para los instrumentos de cambio Doppler.

Los estudios de estabilidad se pueden hacer convenientemente usando DLS. Las mediciones periódicas de DLS de una muestra pueden mostrar si las partículas se agregan con el tiempo al ver si el radio hidrodinámico de la partícula aumenta. Si las partículas se agregan, habrá una mayor población de partículas con un radio mayor. En algunas máquinas DLS, la estabilidad en función de la temperatura puede analizarse controlando la temperatura in situ .