APUNTES DE GEODESIA

aplicaciones, vea Aplanamiento (desambiguación) .

Un círculo de un radio de uncomprimido a una elipse.

Una esfera de radio uncomprime a un elipsoide achatado de revolución.

El aplanamiento es una medida de la compresión de un círculo o esfera a lo largo de un diámetro para formar una elipse o un elipsoide de revolución ( esferoide ) respectivamente. Otros términos utilizados son elipticidad u oblatenidad . La notación habitual para el aplanamiento es f y su definición en términos de los semiejes de la elipse o elipsoide resultante es

$${\ displaystyle \ mathrm {aplanamiento} = f = {\ frac {ab} {a}}.

El factor de compresión es b / a en cada caso. Para la elipse, este factor es también la relación de aspecto de la elipse.

Existen otras dos variantes de aplanamiento (ver más abajo) y cuando es necesario evitar la confusión, el aplanamiento anterior se denomina primer aplanamiento . Las siguientes definiciones se pueden encontrar en los textos estándar ^{[1] [2] [3]} y en los textos web en línea.

Definiciones de aplanamiento [ editar ]

En lo siguiente, a es la dimensión más grande (por ejemplo, eje semimayor), mientras que b es la más pequeña (eje semiminor). Todos los acoplamientos son cero para un círculo ( a  =  b ).

(primero) aplanamiento	$${\ displaystyle f \, \!}	$${\ displaystyle {\ frac {ab} {a}} \, \!}	Fundamental. Los elipsoides de referencia geodésicos se especifican dando$${\ displaystyle 1 / f \, \!}
segundo aplanamiento	$${\ displaystyle f '\, \!}	$${\ displaystyle {\ frac {ab} {b}} \, \!}	Raramente usado.
tercer aplanamiento	$${\ displaystyle n, \ quad (f '') \, \!}	$${\ displaystyle {\ frac {ab} {a + b}} \, \!}	Se utiliza en cálculos geodésicos como un pequeño parámetro de expansión. [6]

Identidades que implican aplanamiento [ editar ]

Los aplanamientos están relacionados con otros parámetros de la elipse. Por ejemplo:

{\ displaystyle {\ begin {alineado} b & = a (1-f) = a \ left ({\ frac {1-n} {1 + n}} \ right), \\ e ^ {2} & = 2f -f ^ {2} = {\ frac {4n} {(1 + n) ^ {2}}}. \\ end {alineado}}}

dónde $${\ displaystyle e}Es la excentricidad .

Valores numericos para planetas [ editar ]

Para el elipsoide WGS84 para modelar la Tierra , los valores que definen son ^[7]

a (radio ecuatorial): 6 378 137.0 m

1 / f (aplanamiento inverso): 298.257 223 563

de la cual se deriva

b (radio polar): 6 356 752.3142 m,

de modo que la diferencia entre los semiejes mayor y menor es de 21.385 km (13 mi). (Esto es solo un 0,335% del eje principal, por lo que una representación de la Tierra en una pantalla de computadora tendría un tamaño de 300px por 299px. Debido a que esto sería virtualmente indistinguible de una esfera que se muestra de 300px por 300px, las ilustraciones generalmente exageran enormemente el aplanamiento casos en los que la imagen debe representar la oblatenidad de la Tierra.)

Otros valores en el Sistema Solar son Jupiter ,   f  = 1/16; Saturno ,   f  = 1/10, la Luna  f  = 1/900. El aplanamiento del sol se trata de9 × 10 ⁻⁶ .

Origen del aplanamiento [ editar ]

En 1687, Isaac Newton publicó los Principia en los que incluyó una prueba de que un cuerpo de fluido autoligitado en equilibrio toma la forma de un elipsoide de revolución oblato (un esferoide ). ^[8] La cantidad de aplanamiento depende de la densidad y el equilibrio de la fuerza gravitacional y la fuerza centrífuga .

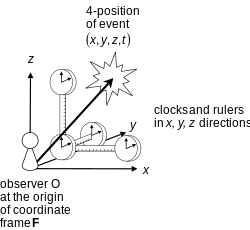
 marco de referencia (o marco de referencia ) consiste en un sistema de coordenadas abstracto y el conjunto de puntos de referencia físicos que fijan (ubican y orientan) de forma única el sistema de coordenadas y estandarizan las mediciones.

En n dimensiones, n + 1 puntos de referencia son suficientes para definir completamente un marco de referencia. Usando coordenadas rectangulares (cartesianas) , se puede definir un marco de referencia con un punto de referencia en el origen y un punto de referencia en una unidad de distancia a lo largo de cada uno de los n ejes de coordenadas.

En la relatividad de Einstein , los marcos de referencia se utilizan para especificar la relación entre un observador en movimiento y el fenómeno o fenómenos bajo observación. En este contexto, la frase a menudo se convierte en " marco de referencia de observación " (o " marco de referencia de observación "), lo que implica que el observador está en reposo en el marco, aunque no necesariamente se encuentra en su origen . Un marco de referencia relativista incluye (o implica) el tiempo de coordenadas , que no corresponde a los diferentes marcos que se mueven entre sí. La situación difiere así de la relatividad galileana., donde todos los tiempos de coordenadas posibles son esencialmente equivalentes.

Diferentes aspectos del "marco de referencia" [ editar ]

La necesidad de distinguir entre los diversos significados del "marco de referencia" ha llevado a una variedad de términos. Por ejemplo, a veces el tipo de sistema de coordenadas se adjunta como un modificador, como en el marco de referencia cartesiano . A veces se enfatiza el estado de movimiento, como en el marco de referencia giratorio . A veces, la forma en que se transforma en marcos considerados como relacionados se enfatiza como en el marco de referencia de Galilea . A veces los marcos se distinguen por la escala de sus observaciones, como en los marcos de referencia microscópicos y macroscópicos . ^[1]

En este artículo, el término marco de referencia de observación se usa cuando el énfasis está en el estado de movimiento y no en la elección de coordenadas o el carácter de las observaciones o el aparato de observación. En este sentido, un marco de referencia de observación permite el estudio del efecto del movimiento en toda una familia de sistemas de coordenadas que podrían adjuntarse a este marco. Por otro lado, un sistema de coordenadas puede emplearse para muchos propósitos en los que el estado de movimiento no es la principal preocupación. Por ejemplo, un sistema de coordenadas puede ser adoptado para aprovechar la simetría de un sistema. En una perspectiva aún más amplia, la formulación de muchos problemas en física emplea coordenadas generalizadas , modos normaleso vectores propios , que solo están indirectamente relacionados con el espacio y el tiempo. Parece útil divorciarse de los diversos aspectos de un marco de referencia para la discusión a continuación. Por lo tanto, tomamos marcos de referencia de observación, sistemas de coordenadas y equipos de observación como conceptos independientes, separados de la siguiente manera:

• Un marco de observación (como un marco inercial o un marco de referencia no inercial ) es un concepto físico relacionado con el estado de movimiento.
• Un sistema de coordenadas es un concepto matemático, que equivale a una elección del lenguaje utilizado para describir las observaciones. ^[2] En consecuencia, un observador en un marco de referencia de observación puede optar por emplear cualquier sistema de coordenadas (cartesiano, polar, curvilíneo, generalizado, ...) para describir las observaciones realizadas a partir de ese marco de referencia. Un cambio en la elección de este sistema de coordenadas no cambia el estado de movimiento de un observador, y por lo tanto no implica un cambio en el marco de referencia de observación del observador . Este punto de vista se puede encontrar en otros lugares también. ^[3] Lo cual no es para negar que algunos sistemas de coordenadas pueden ser una mejor opción para algunas observaciones que otros.

• La elección de qué medir y con qué aparato de observación es un asunto separado del estado de movimiento del observador y la elección del sistema de coordenadas.

Aquí hay una cita aplicable a los marcos de observación en movimiento. $${\ displaystyle {\ mathfrak {R}}}y varios sistemas de coordenadas tridimensionales euclidianos asociados [ R , R ′ , etc. ]: ^[4]

"

Primero introducimos la noción de marco de referencia , en sí misma relacionada con la idea deobservador : el marco de referencia es, en cierto sentido, el "espacio euclidiano llevado por el observador". Démosle una definición más matemática: ... el marco de referencia es ... el conjunto de todos los puntos en el espacio euclidiano con el movimiento rígido del cuerpo del observador. El marco, denotado$${\ displaystyle {\ mathfrak {R}}}, se dice que se mueve con el observador ... Las posiciones espaciales de las partículas están etiquetadas con relación a un marco $${\ displaystyle {\ mathfrak {R}}}mediante el establecimiento de un sistema de coordenadas R con origen O . El conjunto de ejes correspondiente, compartiendo el movimiento del cuerpo rígido del marco.$${\ displaystyle {\ mathfrak {R}}}, se puede considerar para dar una realización física de $${\ displaystyle {\ mathfrak {R}}}. En un marco$${\ displaystyle {\ mathfrak {R}}}Las coordenadas se cambian deR a R ′ llevando a cabo, en cada instante de tiempo, la misma transformación de coordenadas en los componentes de objetos intrínsecos (vectores y tensores) introducidos para representar cantidades físicas en este cuadro .

”

y esto en la utilidad de separar las nociones de $${\ displaystyle {\ mathfrak {R}}}y [ R , R ' , etc. ]: ^[5]

"

Como señaló Brillouin, se debe hacer una distinción entre conjuntos matemáticos de coordenadas y marcos físicos de referencia. La ignorancia de tal distinción es la fuente de mucha confusión ... las funciones dependientes, como la velocidad, por ejemplo, se miden con respecto a un marco de referencia físico, pero uno es libre de elegir cualquier sistema de coordenadas matemáticas en el que se especifiquen las ecuaciones.

”

y esto, también en la distinción entre $${\ displaystyle {\ mathfrak {R}}}y [ R , R ' , etc. ]: ^[6]

"

La idea de un marco de referencia es realmente muy diferente de la de un sistema de coordenadas. Los marcos difieren justo cuando definen diferentes espacios (conjuntos de puntosde descanso ) o tiempos (conjuntos de eventos simultáneos). Así que las ideas de un espacio, un tiempo, de descanso y simultaneidad, van de la misma manera que las del marco. Sin embargo, un mero cambio de origen, o una rotación puramente espacial de coordenadas espaciales resulta en un nuevo sistema de coordenadas. Así que los marcos corresponden en el mejor de los casos a las clases de sistemas de coordenadas.

”

y de JD Norton: ^[7]

"

En los desarrollos tradicionales de la relatividad especial y general, ha sido costumbre no distinguir entre dos ideas muy distintas. La primera es la noción de un sistema de coordenadas, entendida simplemente como la asignación suave e invertible de cuatro números a eventos en vecindarios del espacio-tiempo. El segundo, el marco de referencia, se refiere a un sistema idealizado utilizado para asignar dichos números [...] Para evitar restricciones innecesarias, podemos separar esta disposición de las nociones métricas. […] De especial importancia para nuestros propósitos es que cada marco de referencia tiene un estado de movimiento definido en cada evento de espacio-tiempo. […] En el contexto de la relatividad especial y mientras nos limitemos a los marcos de referencia en el movimiento inercial, entonces, poco de la importancia depende de la diferencia entre un marco de referencia inercial y el sistema de coordenadas inercial que induce. Esta cómoda circunstancia cesa inmediatamente una vez que comenzamos a considerar los marcos de referencia en movimientos no uniformes incluso dentro de la relatividad especial ... Más recientemente, para negociar las ambigüedades evidentes del tratamiento de Einstein, la noción de marco de referencia ha reaparecido como una estructura distinta de un sistema de coordenadas. .

”

Brading y Castellani llevan la discusión más allá de los simples sistemas de coordenadas espacio-temporales. ^{[8] La} extensión para coordinar sistemas utilizando coordenadas generalizadas subyace a las formulaciones hamiltoniana y lagrangiana ^[9] de la teoría cuántica de campos , la mecánica relativista clásica y la gravedad cuántica . ^{[10] [11] [12] [13] [14]}

Sistemas de coordenadas [ editar ]

Artículo principal: Sistemas de coordenadas.

Ver también: coordenadas generalizadas y convenciones de ejes.

Un O observador, situado en el origen de un conjunto local de las coordenadas - un marco de referencia F . El observador en este cuadro usa las coordenadas ( x, y, z, t ) para describir un evento de espacio-tiempo, mostrado como una estrella.

Aunque el término "sistema de coordenadas" se usa a menudo (particularmente por los físicos) en un sentido no técnico, el término "sistema de coordenadas" tiene un significado preciso en matemáticas, y a veces eso es lo que el físico también quiere decir.

Un sistema de coordenadas en matemáticas es una faceta de la geometría o del álgebra , ^[15] [16] en particular, una propiedad de múltiples (por ejemplo, en física, espacios de configuración o espacios de fase ). ^[17] [18] Las coordenadas de un punto r en un espacio n -dimensional son simplemente un conjunto ordenado de nnúmeros: ^[19] [20]

$${\ displaystyle \ mathbf {r} = [x ^ {1}, \ x ^ {2}, \ \ dots, \ x ^ {n}].}

En un espacio general de Banach , estos números podrían ser (por ejemplo) coeficientes en una expansión funcional como una serie de Fourier . En un problema físico, podrían ser coordenadas del espacio-tiempo o amplitudes de modo normal . En un diseño de robot , podrían ser ángulos de rotaciones relativas, desplazamientos lineales o deformaciones de las juntas . ^[21] Aquí supondremos que estas coordenadas se pueden relacionar con un sistema de coordenadas cartesianas mediante un conjunto de funciones:

$${\ displaystyle x ^ {j} = x ^ {j} (x, \ y, \ z, \ \ dots), \ quad j = 1, \ \ dots, \ n,}

donde x , y , z , etc. son las n coordenadas cartesianas del punto. Dadas estas funciones, las superficies de coordenadas están definidas por las relaciones:

$${\ displaystyle x ^ {j} (x, y, z, \ dots) = \ mathrm {constant}, \ quad j = 1, \ \ dots, \ n.}

La intersección de estas superficies define líneas de coordenadas . En cualquier punto seleccionado, las tangentes a las líneas de coordenadas que se cruzan en ese punto definen un conjunto de vectores de base { e ₁ , e ₂ , ..., e _n } en ese punto. Es decir: ^[22]

$${\ displaystyle \ mathbf {e} _ {i} (\ mathbf {r}) = \ lim _ {\ epsilon \ rightarrow 0} {\ frac {\ mathbf {r} \ left (x ^ {1}, \ \ puntos, \ x ^ {i} + \ epsilon, \ \ dots, \ x ^ {n} \ right) - \ mathbf {r} \ left (x ^ {1}, \ \ dots, \ x ^ {i} , \ \ dots, \ x ^ {n} \ right)} {\ epsilon}}, \ quad i = 1, \ \ dots, \ n,}

Que puede normalizarse para que sea de longitud unitaria. Para más detalles ver coordenadas curvilíneas .

Las superficies de coordenadas, las líneas de coordenadas y los vectores de base son componentes de un sistema de coordenadas . ^[23] Si los vectores de base son ortogonales en cada punto, el sistema de coordenadas es un sistema de coordenadas ortogonal .

Un aspecto importante de un sistema de coordenadas es su tensor métrico g _ik , que determina la longitud del arco ds en el sistema de coordenadas en términos de sus coordenadas: ^[24]

$${\ displaystyle (ds) ^ {2} = g_ {ik} \ dx ^ {i} \ dx ^ {k},}

Donde se suman los índices repetidos.

Como se desprende de estas observaciones, un sistema de coordenadas es una construcción matemática , parte de un sistema axiomático . No hay una conexión necesaria entre los sistemas de coordenadas y el movimiento físico (o cualquier otro aspecto de la realidad). Sin embargo, los sistemas de coordenadas pueden incluir el tiempo como una coordenada y pueden usarse para describir el movimiento. Por lo tanto, las transformaciones de Lorentz y las transformaciones de Galileo se pueden ver como transformaciones de coordenadas .

Los temas generales y específicos de los sistemas de coordenadas se pueden seguir siguiendo los enlaces de Ver también a continuación.

Marcos de referencia observacionales [ editar ]

Artículo principal: Marco de referencia inercial.

Tres marcos de referencia en la relatividad especial. El marco negro está en reposo. El cuadro imprimado se mueve al 40% de la velocidad de la luz, y el cuadro imprimado doble al 80%. Observe el cambio similar a una tijera a medida que aumenta la velocidad.

Un marco de referencia de observación , a menudo referido como un marco de referencia físico , un marco de referencia , o simplemente un marco , es un concepto físico relacionado con un observador y el estado de movimiento del observador. Aquí adoptamos la opinión expresada por Kumar y Barve: un marco de referencia de observación se caracteriza solo por su estado de movimiento . ^[25] Sin embargo, hay falta de unanimidad en este punto. En la relatividad especial, la distinción se hace a veces entre un observador y un marco . Según este punto de vista, un marcoes un observador.más una celosía de coordenadas construida para ser un conjunto ortonormal de diestros de vectores espaciales perpendiculares a un vector de tiempo. Ver a Doran. ^[26] Esta vista restringida no se usa aquí, y no se adopta universalmente incluso en discusiones de relatividad. ^[27] [28] En la relatividad general, el uso de sistemas de coordenadas generales es común (ver, por ejemplo, la solución de Schwarzschild para el campo gravitacional fuera de una esfera aislada ^[29] ).

Hay dos tipos de marco de referencia observacional: inercial y no inercial . Un marco de referencia inercial se define como uno en el que todas las leyes de la física toman su forma más simple. En la relatividad especial, estos marcos están relacionados por las transformaciones de Lorentz , que están parametrizadas por la rapidez . En la mecánica newtoniana, una definición más restringida solo requiere que la primera ley de Newton sea cierta; es decir, un marco inercial newtoniano es aquel en el que una partícula libre viaja en línea recta a velocidad constante , o está en reposo. Estos marcos están relacionados por transformaciones galileanas.. Estas transformaciones relativistas y newtonianas se expresan en espacios de dimensión general en términos de representaciones del grupo de Poincaré y del grupo de Galileo .

En contraste con el marco inercial, un marco de referencia no inercial es uno en el que se deben invocar fuerzas ficticias para explicar las observaciones. Un ejemplo es un marco de referencia de observación centrado en un punto de la superficie de la Tierra. Este marco de referencia orbita alrededor del centro de la Tierra, que introduce las fuerzas ficticias conocidas como la fuerza de Coriolis , la fuerza centrífuga y la fuerza gravitacional . (Todas estas fuerzas, incluida la gravedad, desaparecen en un marco de referencia verdaderamente inercial, que es uno de caída libre).

Aparato de medida [ editar ]

Otro aspecto de un marco de referencia es el papel del aparato de medición (por ejemplo, relojes y barras) conectado al marco (consulte la cita de Norton más arriba). Esta pregunta no se aborda en este artículo, y es de particular interés en la mecánica cuántica , donde la relación entre el observador y la medición aún está en discusión (ver el problema de medición ).

En experimentos de física, el marco de referencia en el que los dispositivos de medición de laboratorio están en reposo se suele denominar marco de laboratorio o simplemente "marco de laboratorio". Un ejemplo sería el marco en el que los detectores de un acelerador de partículas están en reposo. El marco de laboratorio en algunos experimentos es un marco inercial, pero no se requiere que lo sea (por ejemplo, el laboratorio en la superficie de la Tierra en muchos experimentos de física no es inercial). En los experimentos de física de partículas, a menudo es útil transformar las energías y los momentos de las partículas desde el marco del laboratorio donde se miden, al centro del marco de momento "marco COM" en el que los cálculos a veces se simplifican.

A este respecto, se puede observar que los relojes y barras utilizados a menudo para describir el equipo de medición de los observadores en el pensamiento, en la práctica se reemplazan por una metrología mucho más complicada e indirecta que está conectada a la naturaleza del vacío , y utiliza relojes atómicos que Funciona de acuerdo con el modelo estándar y debe corregirse para la dilatación del tiempo gravitacional . ^[30] (Ver segundo , metro y kilogramo ).

De hecho, Einstein sintió que los relojes y las barras eran simplemente dispositivos de medición convenientes y deberían ser reemplazados por entidades más fundamentales basadas, por ejemplo, en átomos y moléculas. ^[31]

Tipos [ editar ]

• Marcos de referencia fijados en el cuerpo.
• Marcos de referencia fijos en el espacio.
• Marcos de referencia inerciales
• Marcos de referencia no inerciales

Ejemplos de marcos de referencia inerciales [ editar ]

Esta sección no cita ninguna fuente . Por favor, ayuda a mejorar esta sección mediante la adición de citas de fuentes confiables . El material sin fuente puede ser cuestionado y eliminado . ( Julio de 2013 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Ejemplo simple [ editar ]

Figura 1: Dos carros que se mueven a velocidades diferentes pero constantes observadas desde el marco inercial estacionario S unido a la carretera y el marco inercial movible S ′ unido al primer auto.

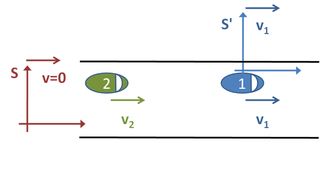
Considere una situación común en la vida cotidiana. Dos autos viajan a lo largo de una carretera, ambos moviéndose a velocidades constantes. Ver Figura 1. En algún momento particular, están separados por 200 metros. El automóvil en frente viaja a 22 metros por segundo y el automóvil detrás viaja a 30 metros por segundo. Si queremos averiguar cuánto tiempo le tomará al segundo auto alcanzar al primero, hay tres "marcos de referencia" obvios que podríamos elegir.

Primero, pudimos observar los dos autos desde el lado de la carretera. Definimos nuestro "marco de referencia" S de la siguiente manera. Nos paramos a un lado de la carretera y arrancamos el cronómetro en el momento exacto en que el segundo automóvil nos pasa, lo que sucede cuando están a una distancia d = 200 m . Como ninguno de los autos se está acelerando, podemos determinar sus posiciones mediante las siguientes fórmulas, donde$${\ displaystyle x_ {1} (t)}es la posición en metros del carro uno después del tiempo t en segundos y$${\ displaystyle x_ {2} (t)}Es la posición del coche dos después del tiempo t .

$${\ displaystyle x_ {1} (t) = d + v_ {1} t = 200 + 22t, \ quad x_ {2} (t) = v_ {2} t = 30t.}

Tenga en cuenta que estas fórmulas predicen en t = 0 s que el primer automóvil está a 200 m por la carretera y el segundo automóvil está justo al lado de nosotros, como se esperaba. Queremos encontrar el momento en el que$${\ displaystyle x_ {1} = x_ {2}}. Por lo tanto, nos propusimos$${\ displaystyle x_ {1} = x_ {2}} y resolver para $${\ displaystyle t}, es decir:

$${\ displaystyle 200 + 22t = 30t,}

$${\ displaystyle 8t = 200,}

$${\ displaystyle t = 25 \ \ mathrm {segundos}.}

Alternativamente, podríamos elegir un marco de referencia S ′ situado en el primer coche. En este caso, el primer automóvil está parado y el segundo automóvil se acerca por detrás a una velocidad de v ₂ - v ₁ = 8 m / s . Con el fin de ponerse al día con el primer coche, tardará un tiempo de d/v ₂ - v ₁ = 200/8 s, es decir, 25 segundos, como antes. Observe cuánto más fácil se vuelve el problema al elegir un marco de referencia adecuado. El tercer marco de referencia posible se adjuntaría al segundo coche. Ese ejemplo se asemeja al caso que acabamos de analizar, excepto que el segundo automóvil está parado y el primer automóvil se mueve hacia atrás a 8 m / s .

Habría sido posible elegir un marco de referencia giratorio y acelerado, moviéndose de una manera complicada, pero esto habría servido para complicar el problema innecesariamente. También es necesario tener en cuenta que uno puede convertir las mediciones realizadas en un sistema de coordenadas a otro. Por ejemplo, suponga que su reloj está funcionando cinco minutos rápido en comparación con la hora estándar local. Si sabe que este es el caso, cuando alguien le pregunta qué hora es, puede deducir cinco minutos de la hora que aparece en su reloj para obtener la hora correcta. Las mediciones que un observador realiza sobre un sistema dependen, por lo tanto, del marco de referencia del observador (se podría decir que el autobús llegó a las tres y cinco, cuando en realidad llegó a las tres).

Ejemplo adicional [ editar ]

Figura 2: Ejemplo de marco de referencia de mente simple

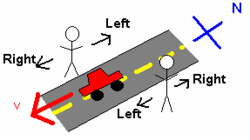
Para un ejemplo simple que involucre solo la orientación de dos observadores, considere a dos personas de pie, una frente a la otra, a cada lado de una calle norte-sur. Vea la Figura 2. Un automóvil pasa por delante de ellos en dirección al sur. Para la persona que mira al este, el carro se movía hacia la derecha. Sin embargo, para la persona que mira hacia el oeste, el automóvil se movía hacia la izquierda. Esta discrepancia se debe a que las dos personas utilizaron dos marcos de referencia diferentes para investigar este sistema.

Para un ejemplo más complejo que involucra observadores en movimiento relativo, considere a Alfred, que está parado al costado de una carretera mirando a un automóvil que lo maneja de izquierda a derecha. En su marco de referencia, Alfred define el lugar donde se encuentra como el origen, el camino como el eje x y la dirección frente a él como el eje y positivo . Para él, el automóvil se mueve a lo largo del eje x con cierta velocidad v en la dirección x positiva . El marco de referencia de Alfred se considera un marco de referencia inercial porque no está acelerando (ignorando efectos como la rotación y la gravedad de la Tierra).

Ahora considere a Betsy, la persona que conduce el auto. Betsy, al elegir su marco de referencia, define su ubicación como el origen, la dirección a su derecha como el eje x positivo y la dirección frente a ella como el eje ypositivo . En este marco de referencia, es Betsy quien está inmóvil y el mundo a su alrededor el que se está moviendo; por ejemplo, cuando pasa por Alfred, lo observa moverse con velocidad v en la dirección y negativa . Si ella está conduciendo al norte, luego hacia el norte es el positivo y -dirección; si se gira hacia el este, al este se convierte en el positivo y -dirección.

Finalmente, como ejemplo de observadores no inerciales, asumamos que Candace está acelerando su auto. Cuando ella pasa a su lado, Alfred mide su aceleración y descubre que es una dirección x negativa . Suponiendo que la aceleración de Candace sea constante, ¿qué aceleración mide Betsy? Si la velocidad v de Betsy es constante, ella se encuentra en un marco de referencia inercial, y encontrará que la aceleración es la misma que Alfred en su marco de referencia, y en la dirección y negativa . Sin embargo, si está acelerando a la velocidad Aen la dirección negativa y (en otras palabras, reduciendo la velocidad), encontrará que la aceleración de Candace es a ′= a - A en la dirección y negativa : un valor más pequeño que el que Alfred ha medido. De manera similar, si está acelerando a la velocidad A en la dirección y positiva (acelerando), observará la aceleración de Candace como a ′ = a + A en la dirección y negativa , un valor mayor que la medida de Alfred.

Los marcos de referencia son especialmente importantes en la relatividad especial , porque cuando un marco de referencia se mueve a una fracción significativa de la velocidad de la luz, el flujo de tiempo en ese marco no se aplica necesariamente a otro marco. La velocidad de la luz se considera la única constante verdadera entre los marcos de referencia en movimiento.

Observaciones [ editar ]

Ver también: la teoría especial de la relatividad y la teoría general de la relatividad

Es importante tener en cuenta algunas suposiciones hechas anteriormente sobre los diversos marcos de referencia inerciales. Newton, por ejemplo, empleó el tiempo universal, como se explica en el siguiente ejemplo. Supongamos que tiene dos relojes, que marcan exactamente la misma frecuencia. Los sincroniza para que ambos se muestren exactamente al mismo tiempo. Los dos relojes ahora están separados y un reloj está en un tren en movimiento rápido, viajando a velocidad constante hacia el otro. Según Newton, estos dos relojes seguirán funcionando al mismo ritmo y ambos mostrarán el mismo tiempo. Newton dice que la tasa de tiempo medida en un marco de referencia debe ser la misma que la tasa de tiempo en otro. Es decir, existe un "universal". el tiempo y todos los demás tiempos en todos los demás marcos de referencia se ejecutarán a la misma velocidad que este tiempo universal, independientemente de su posición y velocidad. Este concepto de tiempo y simultaneidad fue luego generalizado por Einstein en suTeoría especial de la relatividad (1905) donde desarrolló transformaciones entre marcos de referencia inerciales basados ​​en la naturaleza universal de las leyes físicas y su economía de expresión ( transformaciones de Lorentz ).

La definición de marco de referencia inercial también puede extenderse más allá del espacio euclidiano tridimensional. Newton asumió un espacio euclidiano, pero la relatividad general utiliza una geometría más general. Como ejemplo de por qué esto es importante, considere la geometría de un elipsoide. En esta geometría, una partícula "libre" se define como una en reposo o que se desplaza a una velocidad constante en una geodésica.camino. Dos partículas libres pueden comenzar en el mismo punto de la superficie, viajando con la misma velocidad constante en diferentes direcciones. Después de un período de tiempo, las dos partículas colisionan en el lado opuesto del elipsoide. Ambas partículas "libres" viajaron a una velocidad constante, satisfaciendo la definición de que ninguna fuerza estaba actuando. No se produjo ninguna aceleración y la primera ley de Newton se mantuvo así. Esto significa que las partículas estaban en marcos de referencia inerciales. Como ninguna fuerza actuaba, fue la geometría de la situación lo que hizo que las dos partículas se encontraran nuevamente. De manera similar, ahora es común describir ^[32] que existimos en una geometría de cuatro dimensiones conocida como espacio-tiempo. En esta imagen, la curvatura de este espacio 4D es responsable de la forma en que dos cuerpos con masa se unen, incluso si no hay fuerzas actuando. Esta curvatura del espacio-tiempo reemplaza la fuerza conocida como gravedad en la mecánica newtoniana y la relatividad especial.

Marcos no inerciales [ editar ]

Artículos principales: Fuerza ficticia , Marco no inercial y Marco de referencia giratorio.

Aquí se considera la relación entre los marcos de referencia observacionales inerciales y no inerciales. La diferencia básica entre estos marcos es la necesidad en marcos no inerciales de fuerzas ficticias, como se describe a continuación.

Un marco de referencia acelerado a menudo se define como el marco "cebado", y todas las variables que dependen de ese cuadro se anotan con números primos, por ejemplo, x ' , y' , a ' .

El vector desde el origen de un sistema de referencia inercial para el origen de un sistema de referencia acelerado se notated comúnmente como R . Dado un punto de interés que existe en ambos marcos, el vector desde el origen inercial hasta el punto se llama r , y el vector desde el origen acelerado hasta el punto se llama r '. De la geometría de la situación, obtenemos

$${\ displaystyle \ mathbf {r} = \ mathbf {R} + \ mathbf {r} '.}

Tomando la primera y segunda derivadas de esto con respecto al tiempo, obtenemos

$${\ displaystyle \ mathbf {v} = \ mathbf {V} + \ mathbf {v} ',}

$${\ displaystyle \ mathbf {a} = \ mathbf {A} + \ mathbf {a} '.}

donde V y A son la velocidad y la aceleración del sistema acelerado con respecto al sistema inercial y v y a son la velocidad y la aceleración del punto de interés con respecto al marco inercial.

Estas ecuaciones permiten transformaciones entre los dos sistemas de coordenadas; por ejemplo, ahora podemos escribir la segunda ley de Newton como

$${\ displaystyle \ mathbf {F} = m \ mathbf {a} = m \ mathbf {A} + m \ mathbf {a} '.}

Cuando hay un movimiento acelerado debido a una fuerza ejercida, hay manifestación de inercia. Si un automóvil eléctrico diseñado para recargar su sistema de batería cuando la desaceleración cambia a frenado, las baterías se recargan, lo que ilustra la fuerza física de la manifestación de inercia. Sin embargo, la manifestación de inercia no impide la aceleración (o desaceleración), ya que la manifestación de inercia ocurre en respuesta al cambio en la velocidad debido a una fuerza. Visto desde la perspectiva de un marco de referencia giratorio, la manifestación de inercia parece ejercer una fuerza (ya sea en dirección centrífuga , o en una dirección ortogonal al movimiento de un objeto, el efecto Coriolis ).

Un tipo común de marco de referencia acelerado es un marco que gira y se traduce (un ejemplo es un marco de referencia adjunto a un CD que se reproduce mientras se lleva el reproductor). Esta disposición lleva a la ecuación (ver Fuerza ficticia para una derivación):

$${\ displaystyle \ mathbf {a} = \ mathbf {a} '+ {\ dot {\ boldsymbol {\ omega}}} \ times \ mathbf {r}' +2 {\ boldsymbol {\ omega}} \ times \ mathbf {v} '+ {\ boldsymbol {\ omega}} \ times ({\ boldsymbol {\ omega}} \ times \ mathbf {r}') + \ mathbf {A} _ {0},}

o, para resolver la aceleración en el cuadro acelerado,

$${\ displaystyle \ mathbf {a} '= \ mathbf {a} - {\ dot {\ boldsymbol {\ omega}}} \ times \ mathbf {r}' -2 {\ boldsymbol {\ omega}} \ times \ mathbf {v} '- {\ boldsymbol {\ omega}} \ times ({\ boldsymbol {\ omega}} \ times \ mathbf {r}') - \ mathbf {A} _ {0}.}

Multiplicando a través de la masa m da

$${\ displaystyle \ mathbf {F} '= \ mathbf {F} _ {\ mathrm {physical}} + \ mathbf {F}' _ {\ mathrm {Euler}} + \ mathbf {F} '_ {\ mathrm { Coriolis}} + \ mathbf {F} '_ {\ mathrm {centripetal}} -m \ mathbf {A} _ {0},}

dónde

$${\ displaystyle \ mathbf {F} '_ {\ mathrm {Euler}} = - m {\ dot {\ boldsymbol {\ omega}}} \ times \ mathbf {r}'}( Fuerza de Euler ),

$${\ displaystyle \ mathbf {F} '_ {\ mathrm {Coriolis}} = - 2m {\ boldsymbol {\ omega}} \ times \ mathbf {v}'}( Fuerza de Coriolis ),

$${\ displaystyle \ mathbf {F} '_ {\ mathrm {centrifugal}} = - m {\ boldsymbol {\ omega}} \ times ({\ boldsymbol {\ omega}} \ times \ mathbf {r}') = m (\ omega ^ {2} \ mathbf {r} '- ({\ boldsymbol {\ omega}} \ cdot \ mathbf {r}') {\ boldsymbol {\ omega}})}( fuerza centrífuga ).