SERIES MATEMÁTICAS

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

La serie 1 + 1 + 1 + 1 + ⋯

Despues de alisar

Comportamiento asintótico del alisado. El y intercepción de la línea es - 1/2 . ^[1]

En matemáticas , 1 + 1 + 1 + 1 + , también escrito$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} n ^ {0}}, $${\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1 ^ {n}}, o simplemente $${\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1}, es una serie divergente , lo que significa que su secuencia de sumas parciales no converge a un límite en los números reales . La secuencia 1 ⁿ puede pensarse como una serie geométrica con la relación común 1. A diferencia de otras series geométricas con relación racional(excepto −1 ), no converge ni en los números reales ni en los números p -adic para algunas  p . En el contexto de la recta numérica extendida

$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} 1 = + \ infty \ ,,}

Ya que su secuencia de sumas parciales aumenta monótonamente sin límite.

Cuando la suma de n ^{0 se} produce en aplicaciones físicas , a veces puede interpretarse mediante la regularización de la función zeta , como el valor en s = 0 de la función zeta de Riemann

$${\ displaystyle \ zeta (s) = \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {s}}} = {\ frac {1} {1-2 ^ {1 -s}}} \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {n ^ {s}}} \ ,,}

Sin embargo, las dos fórmulas dadas anteriormente no son válidas en cero, por lo que se podría intentar la continuación analítica de la función zeta de Riemann,

$${\ displaystyle \ zeta (s) = 2 ^ {s} \ pi ^ {s-1} \ \ sin \ left ({\ frac {\ pi s} {2}} \ right) \ \ Gamma (1-s ) \ \ zeta (1-s) \ !,}

Usando este se obtiene (dado que Γ (1) = 1 ),

$${\ displaystyle \ zeta (0) = {\ frac {1} {\ pi}} \ lim _ {s \ rightarrow 0} \ \ sin \ left ({\ frac {\ pi s} {2}} \ right) \ \ zeta (1-s) = {\ frac {1} {\ pi}} \ lim _ {s \ rightarrow 0} \ \ left ({\ frac {\ pi s} {2}} - {\ frac { \ pi ^ {3} s ^ {3}} {48}} + ... \ derecha) \ \ izquierda (- {\ frac {1} {s}} + ... \ derecha) = - {\ frac {1} {2}}}

donde la expansión de la serie de potencias para ζ ( s ) sobre s = 1 sigue porque ζ ( s ) tiene un polo simple de residuo allí. En este sentido 1 + 1 + 1 + 1 + ⋯ = ζ (0) = - 1/2 .

Emilio Elizalde presenta una anécdota sobre las actitudes hacia la serie:

En un corto período de menos de un año, dos distinguidos físicos, A. Slavnov y F. Yndurain , dieron seminarios en Barcelona sobre diferentes temas. Era notable que, en ambas presentaciones, en algún momento el altavoz se dirigió al público con estas palabras: 'Como todo el mundo sabe, 1 + 1 + 1 + ⋯ = - 1/2 '. Implicando quizás: Si no lo sabes, no sirve de nada seguir escuchando.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Las primeras cuatro sumas parciales de la serie 1 + 2 + 3 + 4 + ⋯ . La parábola es su asíntota suavizada; su y intercepción es - 1/12  . ^[1]

La serie infinita cuyos términos son los números naturales 1 + 2 + 3 + 4 + es una serie divergente . El n º suma parcial de la serie es el número triangular

$${\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}},}

que aumenta sin límite a medida que n va al infinito . Debido a que la secuencia de sumas parciales no puede converger a un límite finito , la serie no tiene una suma.

Aunque a primera vista la serie parece no tener ningún valor significativo, puede manipularse para obtener una serie de resultados matemáticamente interesantes. Por ejemplo, muchos métodos de suma se usan en matemáticas para asignar valores numéricos incluso a una serie divergente. En particular, los métodos de regularización función zeta y suma Ramanujan asignar la serie un valor de - 1/12  , que se expresa por una fórmula famoso, ^[2]

$${\ displaystyle 1 + 2 + 3 + 4 + \ cdots = - {\ frac {1} {12}},}

donde el lado izquierdo debe interpretarse como el valor obtenido utilizando uno de los métodos de suma mencionados anteriormente y no como la suma de una serie infinita en su significado habitual. Estos métodos tienen aplicaciones en otros campos, como el análisis complejo , la teoría cuántica de campos y la teoría de cuerdas . ^[3]

En una monografía sobre la teoría de Moonshine , Terry Gannon llama a esta ecuación "una de las fórmulas más notables de la ciencia".

Sumas parciales [ editar ]

Los primeros seis números triangulares.

Artículo principal: Número triangular

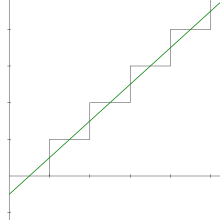
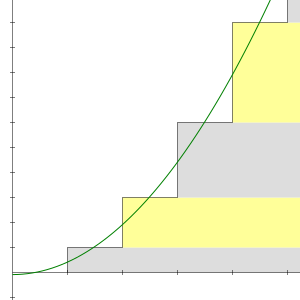
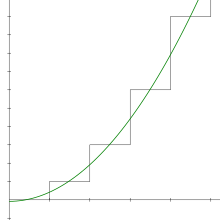
Las sumas parciales de la serie 1 + 2 + 3 + 4 + 5 + 6 + ⋯ son 1, 3, 6, 10, 15 , etc. El n º suma parcial está dada por una fórmula simple:

$${\ displaystyle \ sum _ {k = 1} ^ {n} k = {\ frac {n (n + 1)} {2}}.}

Esta ecuación era conocida por los pitagóricos en el siglo VI a. ^{[5] Los}números de esta forma se llaman números triangulares , porque se pueden organizar como un triángulo equilátero.

La secuencia infinita de los números triangulares se desvía a + ∞, así que, por definición, la serie infinita 1 + 2 + 3 + 4 + también difiere a + ∞. La divergencia es una consecuencia simple de la forma de la serie: los términos no se acercan a cero, por lo que la serie difiere por el término prueba .

Sumabilidad [ editar ]

Entre las series divergentes clásicas, 1 + 2 + 3 + 4 + es relativamente difícil de manipular en un valor finito. Se utilizan muchos métodos de suma para asignar valores numéricos a series divergentes, algunas más poderosas que otras. Por ejemplo, Cesàro suma es un método bien conocido que resume la serie de Grandi , la serie ligeramente divergente 1 - 1 + 1 - 1 + ⋯ , a 1/2 . Abel suma es un método más potente que no sólo resume la serie de Grandi a 1/2 , pero también resume las series más difíciles 1 - 2 + 3 - 4 + ⋯ a 1/4 .

A diferencia de las series anteriores, 1 + 2 + 3 + 4 + no es Cesàro sumable ni Abel sumable. Esos métodos funcionan en series divergentes oscilantes, pero no pueden producir una respuesta finita para una serie que diverge a + ∞. ^[6] La mayoría de las definiciones más elementales de la suma de una serie divergente son estables y lineales, y cualquier método que sea estable y lineal no puede sumar 1 + 2 + 3 + ⋯ a un valor finito; vea abajo. Se requieren métodos más avanzados, como la regularización de la función zeta o la suma de Ramanujan . También es posible argumentar por el valor de - 1/12  usando algunas heurísticas ásperas relacionados con estos métodos.

Heurística [ editar ]

Paso del primer cuaderno de Ramanujan que describe la "constante" de la serie

Srinivasa Ramanujan presentó dos derivaciones de " 1 + 2 + 3 + 4 + ⋯ = - 1/12 " en el capítulo 8 de su primera notebook. ^{[7] [8] [9]} La derivación más simple, menos rigurosa, se realiza en dos pasos, de la siguiente manera.

La primera idea clave es que la serie de números positivos 1 + 2 + 3 + 4 + res se asemeja mucho a la serie alterna 1 - 2 + 3 - 4 + ⋯ . La última serie también es divergente, pero es mucho más fácil trabajar con ella; Existen varios métodos clásicos que le asignan un valor, que se han explorado desde el siglo XVIII. ^[10]

Para transformar la serie 1 + 2 + 3 + 4 + ⋯ en 1 - 2 + 3 - 4 + , se pueden restar 4 del segundo término, 8 del cuarto término, 12 del sexto término, etc. . La cantidad total a restar es 4 + 8 + 12 + 16 + ⋯ , que es 4 veces la serie original. Estas relaciones se pueden expresar utilizando el álgebra. Cualquiera que sea la "suma" de la serie, llámala c = 1 + 2 + 3 + 4 + ⋯. Luego multiplica esta ecuación por 4 y resta la segunda ecuación de la primera:

{\ displaystyle {\ begin {alignat} {7} c & {} = {} & 1 + 2 && {} + 3 + 4 && {} + 5 + 6 + \ cdots \\ 4c & {} = {} & 4 && {} + 8 && { } +12+ \ cdots \\ c-4c & {} = {} & 1-2 && {} + 3-4 && {} + 5-6 + \ cdots \\\ end {alignat}}}

La segunda idea clave es que la serie alterna 1 - 2 + 3 - 4 + es la expansión de la serie de potencia formal de la función 1/(1 + x ) ² pero con x definida como 1. En consecuencia, Ramanujan escribe:

$${\ displaystyle -3c = 1-2 + 3-4 + \ cdots = {\ frac {1} {(1 + 1) ^ {2}}} = {\ frac {1} {4}}}

Dividiendo ambos lados por -3, se obtiene c  =  - 1/12  .

En términos generales, es incorrecto manipular series infinitas como si fueran sumas finitas. Por ejemplo, si los ceros se insertan en posiciones arbitrarias de una serie divergente, es posible llegar a resultados que no son coherentes, y mucho menos coherentes con otros métodos. En particular, el paso 4 c = 0 + 4 + 0 + 8 + no está justificado solo por la ley de identidad aditiva . Para un ejemplo extremo, agregar un solo cero al frente de la serie puede llevar a resultados inconsistentes. ^[1]

Una forma de remediar esta situación, y restringir los lugares donde se pueden insertar ceros, es hacer un seguimiento de cada término de la serie adjuntando una dependencia de alguna función. ^[11] En la serie 1 + 2 + 3 + 4 + , cada término n es solo un número. Si el término n se promueve a una función n ^−s , donde s es una variable compleja, entonces se puede garantizar que solo se agreguen términos similares. La serie resultante se puede manipular de una manera más rigurosa, y la variable s se puede establecer en -1 más tarde. La implementación de esta estrategia se llama regularización de la función zeta .

Regularización de la función Zeta [ editar ]

Parcela de ζ ( s ). Para s > 1 , la serie converge y ζ ( s )> 1 . Continuación analítica alrededor del polo en s = 1 conduce a una región de valores negativos, incluyendo ζ (-1) = - 1/12 

En la normalización de la función zeta , la serie.$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} n} es reemplazado por la serie $${\ displaystyle \ sum _ {n = 1} ^ {\ infty} n ^ {- s}}. La última serie es un ejemplo de una serie de Dirichlet . Cuando la parte real de s es mayor que 1, la serie de Dirichlet converge y su suma es la función zeta de Riemann ζ ( s ). Por otro lado, la serie de Dirichlet diverge cuando la parte real de s es menor o igual a 1, por lo que, en particular, la serie 1 + 2 + 3 + 4 + ⋯ que resulta del ajuste s = –1 no converge . La ventaja de la introducción de la función zeta de Riemann es que puede definirse para otros valores de s mediante la continuación analítica . Entonces se puede definir la suma zeta-regularizada de 1 + 2 + 3 + 4 +ser ζ(−1).

A partir de este punto, hay algunas maneras de probar que ζ (-1) = - 1/12  . Un método, a lo largo de las líneas de razonamiento de Euler, ^[12] utiliza la relación entre la función zeta de Riemann y la función eta Dirichlet η ( s ). La función eta se define mediante una serie de Dirichlet alterna, por lo que este método es paralelo a las heurísticas anteriores. Cuando ambas series de Dirichlet convergen, una tiene las identidades:

{\ displaystyle {\ begin {alignat} {7} \ zeta (s) & {} = {} & 1 ^ {- s} +2 ^ {- s} && {} + 3 ^ {- s} + 4 ^ { -s} && {} + 5 ^ {- s} +6 ^ {- s} + \ cdots & \\ 2 \ times 2 ^ {- s} \ zeta (s) & {} = {} & 2 \ times 2 ^ {- s} && {} + 2 \ veces 4 ^ {- s} && {} + 2 \ veces 6 ^ {- s} + \ cdots & \\ left (1-2 ^ {1-s} \ derecha) \ zeta (s) & {} = {} & 1 ^ {- s} -2 ^ {- s} && {} + 3 ^ {- s} -4 ^ {- s} && {} + 5 ^ { -s} -6 ^ {- s} + \ cdots & = \ eta (s) \\\ end {alignat}}}

La identidad $${\ displaystyle (1-2 ^ {1-s}) \ zeta (s) = \ eta (s)}se mantiene cuando ambas funciones se extienden por la continuación analítica para incluir valores de s para los cuales divergen las series anteriores. Sustituyendo s = −1 , se obtiene −3 ζ (−1) = η (−1). Ahora, computar η (−1) es una tarea más fácil, ya que la función eta es igual a la suma de Abel de su serie definitoria, ^[13] que es un límite unilateral :

$${\ displaystyle -3 \ zeta (-1) = \ eta (-1) = \ lim _ {x \ a 1 ^ {-}} \ left (1-2x + 3x ^ {2} -4x ^ {3} + \ cdots \ right) = \ lim _ {x \ to 1 ^ {-}} {\ frac {1} {(1 + x) ^ {2}}} = {\ frac {1} {4}}}

Dividiendo ambos lados por -3, uno obtiene ζ (-1) = - 1/12  .

Corte regularización [ editar ]

La serie 1 + 2 + 3 + 4 + ⋯

Despues de alisar

Comportamiento asintótico del alisado. El y intercepción de la parábola es - 1/12  . ^[1]

El método de regularización utilizando una función de corte puede "alisar" la serie para llegar a - 1/12  . El suavizado es un puente conceptual entre la regularización de la función zeta, con su dependencia en el análisis complejo y la suma de Ramanujan, con su acceso directo a la fórmula de Euler-Maclaurin . En cambio, el método opera directamente en transformaciones conservadoras de la serie, utilizando métodos del análisis real .

La idea es reemplazar la serie discreta de mal comportamiento. $${\ displaystyle \ sum _ {n = 0} ^ {N} n} con una versión alisada

$${\ displaystyle \ sum _ {n = 0} ^ {\ infty} nf \ left ({\ frac {n} {N}} \ right)},

donde f es una función de corte con propiedades apropiadas. La función de corte debe normalizarse a f (0) = 1 ; Esta es una normalización diferente de la utilizada en las ecuaciones diferenciales. La función de corte debe tener suficientes derivados limitados para suavizar las arrugas en la serie, y debe decaer a 0 más rápido de lo que crece la serie. Por conveniencia, uno puede requerir que f sea liso , acotado y que sea compacto . Uno puede entonces probar que esta suma alisada es asintótica a - 1/12  + CN ² , donde CEs una constante que depende de f . El término constante de la expansión asintótica no depende de f : es necesariamente el mismo valor dado por continuación analítica,  - 1/12  . ^[1]

Ramanujan sumatoria [ editar ]

La suma Ramanujan de 1 + 2 + 3 + 4 + ⋯ es también  - 1/12  . Ramanujan escribió en su segunda carta a GH Hardy , fechada el 27 de febrero de 1913:

"Estimado señor, me complace mucho leer detenidamente su carta del 8 de febrero de 1913. Esperaba una respuesta suya similar a la que un Profesor de Matemáticas de Londres escribió pidiéndome que estudie cuidadosamente la Serie Infinita de Bromwich y que no caiga. . en las trampas de las series divergentes ... le dije que la suma de un número infinito de términos de la serie: 1 + 2 + 3 + 4 + ⋯ = - 1/12 . debajo de mi teoría, si te digo esto usted lo hará en Una vez, señale el manicomio como mi objetivo. Me dilato simplemente para convencerlo de que no podrá seguir mis métodos de prueba si indico las líneas en las que procedo en una sola letra ... " ^{[14 ]} 

La suma de Ramanujan es un método para aislar el término constante en la fórmula de Euler-Maclaurin para las sumas parciales de una serie. Para una función f , la suma clásica de Ramanujan de la serie.$${\ displaystyle \ sum _ {k = 1} ^ {\ infty} f (k)} Se define como

$${\ displaystyle c = - {\ frac {1} {2}} f (0) - \ sum _ {k = 1} ^ {\ infty} {\ frac {B_ {2k}} {(2k)!}} f ^ {(2k-1)} (0),}

donde f ^(2 k -1) es la (2 k  - 1) -ésima derivada de f y B _2 k es la 2 k ésimo número de Bernoulli : B ₂ = 1/6 , B ₄ = - 1/30  , y así en. Al establecer f ( x ) = x , la primera derivada de f es 1, y todo otro término desaparece, por lo que: ^[15]

$${\ displaystyle c = - {\ frac {1} {6}} \ times {\ frac {1} {2!}} = - {\ frac {1} {12}}.

Para evitar inconsistencias, la teoría moderna de la suma de Ramanujan requiere que f sea ​​"regular" en el sentido de que los derivados de orden superior de f decaen lo suficientemente rápido para que los términos restantes de la fórmula de Euler-Maclaurin tiendan a 0. Ramanujan asumió esto tácitamente propiedad. ^[15] El requisito de regularidad impide el uso de la suma de Ramanujan en series espaciadas como 0 + 2 + 0 + 4 + ⋯ , porque ninguna función regular toma esos valores. En su lugar, dicha serie debe interpretarse mediante la regularización de la función zeta. Por esta razón, Hardy recomienda "gran precaución" al aplicar las sumas de Ramanujan de series conocidas para encontrar las sumas de series relacionadas. ^[dieciséis]

Falla de métodos de suma lineales estables [ editar ]

Un método de suma que sea lineal y estable no puede sumar la serie 1 + 2 + 3 + a ningún valor finito. (Estable significa que agregar un término al comienzo de la serie aumenta la suma en la misma cantidad). Esto se puede ver de la siguiente manera. Si

1 + 2 + 3 + ⋯ = x

luego agregando 0 a ambos lados da

0 + 1 + 2 + ⋯ = 0 + x = x por estabilidad.

Por linealidad, se puede restar la segunda ecuación de la primera (restando cada componente de la segunda línea de la primera línea en columnas) para obtener

1 + 1 + 1 + ⋯ = x - x = 0.

Sumando 0 a ambos lados nuevamente da

0 + 1 + 1 + 1 + ⋯ = 0,

y restando las dos últimas series da

1 + 0 + 0 + ⋯ = 0

Estabilidad contradictoria.

Por lo tanto, cada método que da un valor finito a la suma 1 + 2 + 3 + no es estable o no es lineal. ^[17]

Física [ editar ]

En la teoría de cuerdas bosónicas , el intento es calcular los posibles niveles de energía de una cuerda, en particular el nivel de energía más bajo. Hablando de manera informal, cada armónico de la cuerda puede verse como una colección de osciladores de armónicos cuánticos  independientes de D - 2 , uno para cada dirección transversal , donde D es la dimensión del espacio-tiempo. Si la frecuencia de oscilación fundamental es ω,entonces la energía en un oscilador que contribuye al armónico n es nħω/2 . Entonces, al usar las series divergentes, la suma sobre todos los armónicos es - ħω(D- 2)/ 24 . En última instancia, es este hecho, combinado con elteorema de Goddard-Thorn, lo que lleva a que la teoría de cuerdas bosónicas no sea consistente en otras dimensiones que no sean 26. ^[18]

La regularización de 1 + 2 + 3 + 4 + también está involucrada en el cálculo de la fuerza de Casimir para un campo escalar en una dimensión. ^[19] Una función de corte exponencial es suficiente para suavizar la serie, lo que representa el hecho de que las placas conductoras no bloquean arbitrariamente los modos de alta energía. La simetría espacial del problema es responsable de cancelar el término cuadrático de la expansión. Todo lo que queda es el término constante - 1/12  , y el signo negativo de este resultado refleja el hecho de que la fuerza de Casimir es atractivo. ^[20]

Un cálculo similar está involucrado en tres dimensiones, utilizando la función zstein de Epstein en lugar de la función zeta de Riemann. ^[21]

Historia [ editar ]

No está claro si Leonhard Euler resume la serie a - 1/12  . Según Morris Kline , el trabajo inicial de Euler en series divergentes se basó en las expansiones de funciones, de las cuales concluyó 1 + 2 + 3 + 4 + ⋯ = ∞ . ^[22] Según Raymond Ayoub, el hecho de que la serie zeta divergente no sea Abel sumable impidió que Euler usara la función zeta tan libremente como la función eta, y "no pudo haber asignado un significado" a la serie. ^[23] Otros autores han acreditado a Euler con la suma, lo que sugiere que Euler habría extendido la relación entre las funciones zeta y eta a enteros negativos. ^{[24] [25] [26]}En la literatura primaria, la serie 1 + 2 + 3 + 4 + se menciona en la publicación de Euler 1760 De seriebus divergentibus junto con la serie geométrica divergente 1 + 2 + 4 + 8 + ⋯ . Euler insinúa que las series de este tipo tienen sumas finitas y negativas, y explica qué significa esto para las series geométricas, pero no vuelve a discutir 1 + 2 + 3 + 4 + ⋯ . En la misma publicación, Euler escribe que la suma de 1 + 1 + 1 + 1 + es infinita. ^[27]

En los medios populares [ editar ]

La novela de David Leavitt en 2007, The Indian Clerk, incluye una escena en la que Hardy y Littlewood discuten el significado de esta serie. Concluyen que Ramanujan ha redescubierto ζ (−1) y toman la línea de "manicomio" en su segunda carta como una señal de que Ramanujan está jugando con ellos. ^[28]

La obra de Simon McBurney en 2007, A Disappearing Number, se centra en la serie en la escena inicial. El personaje principal, Ruth, entra en una sala de conferencias e introduce la idea de una serie divergente antes de proclamar: "Yo te voy a mostrar algo realmente emocionante", es decir, 1 + 2 + 3 + 4 + ⋯ = - 1/12  . Cuando Ruth se lanza a una derivación de la ecuación funcional de la función zeta, otro actor se dirige a la audiencia, admitiendo que son actores: "Pero las matemáticas son reales. Es aterrador, pero es real". ^[29] [30]

En enero de 2014, Numberphile produjo un video de YouTube en la serie, que reunió más de 1.5 millones de visitas en su primer mes. ^[31] El video de 8 minutos es narrado por Tony Padilla, físico de la Universidad de Nottingham . Padilla comienza con 1 - 1 + 1 - 1 + ⋯ y 1 - 2 + 3 - 4 + ⋯ y relaciona este último con 1 + 2 + 3 + 4 + ⋯ usando una resta término por término similar al argumento de Ramanujan. ^[32] Numberphile también dio a conocer una versión de 21 minutos de la video con Nottingham físico Ed Copeland, que se describe con más detalle cómo 1 - 2 + 3 - 4 + ⋯ = 1/4como una suma Abel y 1 + 2 + 3 + 4 + ⋯ = - 1/12  como ζ (-1). ^[33] Después de recibir quejas sobre la falta de rigor en el primer video, Padilla también escribió una explicación en su página web que relaciona las manipulaciones en el video con las identidades entre las continuaciones analíticas de la serie correspondiente de Dirichlet. ^[34]

En la cobertura de The New York Times del video Numberphile, el matemático Edward Frenkel comentó: "Este cálculo es uno de los secretos mejor guardados de las matemáticas. Nadie en el exterior lo sabe". ^[31]

La cobertura de este tema en el Smithsonian revista describe el video Numberphile engañosa, y señala que la interpretación de la suma como - 1/12 

 se basa en un significado especial para los iguales firman, a partir de las técnicas de la continuación analítica , en el cual equivale medios se asocia con.