SERIES MATEMÁTICAS

Este artículo necesita citas adicionales para su verificación . Por favor, ayudar a mejorar este artículo mediante la adición de citas de fuentes confiables . El material sin fuente puede ser cuestionado y eliminado.  Encuentre fuentes:  "Onda de diente de sierra"  -  noticias  · periódicos  · libros  · erudito  ·JSTOR ( agosto de 2008 ) ( Aprenda cómo y cuándo eliminar este mensaje de plantilla )

Una onda de diente de sierra con límite de banda representada en el dominio del tiempo (superior) y el dominio de la frecuencia (inferior). Lo fundamental es a 220 Hz (A3).

La onda de diente de sierra (u onda de sierra ) es una forma de onda no sinusoidal. Se llama así por su parecido con los dientes de una sierra de dientes planos con un ángulo de inclinación cero .

La convención es que una onda de diente de sierra sube hacia arriba y luego cae bruscamente ^{[ cita requerida ]} . Sin embargo, en una onda de diente de sierra inversa (o inversa), la onda desciende hacia abajo y luego aumenta bruscamente. También se puede considerar el caso extremo de una onda triangular asimétrica . ^[1]

La función lineal por tramos.

$${\ displaystyle x (t) = t- \ underbrace {\ lfloor t \ rfloor} _ {\ operatorname {floor} (t)}}

o

$${\ displaystyle x (t) = t {\ pmod {1}}}

basado en la función de piso del tiempo t es un ejemplo de una onda de diente de sierra con el período 1.

Una forma más general, en el rango de −1 a 1, y con el período a , es

$${\ displaystyle 2 \ left ({\ frac {t} {a}} - \ left \ lfloor {\ frac {1} {2}} + {\ frac {t} {a}} \ right \ rfloor \ right) }

Esta función de diente de sierra tiene la misma fase que la función seno.

Otra función en términos trigonométricos con período p y amplitud a :

$${\ displaystyle y (x) = - {\ frac {2a} {\ pi}} \ arctan \ left (\ cot \ left ({\ frac {x \ pi} {p}} \ right) \ right)}

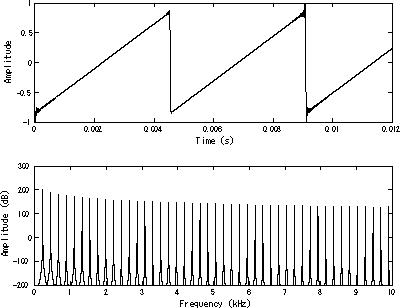
Mientras que una onda cuadrada se construye solo con armónicos impares, el sonido de una onda de diente de sierra es áspero y claro y su espectro contiene armónicos pares e impares de la frecuencia fundamental . Debido a que contiene todos los armónicos de enteros, es una de las mejores formas de onda para la síntesis sustractivade sonidos musicales, especialmente instrumentos de cuerda con arcos, como violines y violonchelos, ya que el comportamiento de la barra de deslizamiento conduce las cuerdas con un diente de sierra. movimiento. ^[2]

	Demostración de diente de sierra aditiva MENÚ 0:00 Onda de diente de sierra de 220Hz creada por armónicos agregados cada segundo sobre la onda sinusoidal.
¿Problemas para reproducir este archivo? Ver la ayuda de los medios .

Un diente de sierra se puede construir utilizando síntesis aditiva . La serie infinita de Fourier.

$${\ displaystyle x _ {\ text {reverso diente de sierra}} (t) = {\ frac {2A} {\ pi}} \ sum _ {k = 1} ^ {\ infty} {(- 1)} ^ {k} {\ frac {\ sin (2 \ pi kft)} {k}}}

converge a una onda de diente de sierra inversa (inversa). Un diente de sierra convencional se puede construir utilizando

$${\ displaystyle x _ {\ mathrm {sawtooth}} (t) = {\ frac {A} {2}} - {\ frac {A} {\ pi}} \ sum _ {k = 1} ^ {\ infty} {(-1)} ^ {k} {\ frac {\ sin (2 \ pi kft)} {k}}}

donde A es la amplitud.

En síntesis digital , estas series solo se suman sobre k, de modo que el armónico más alto, N _max , es menor que la frecuencia de Nyquist (la mitad de la frecuencia de muestreo ). Esta suma generalmente se puede calcular de manera más eficiente con una transformada rápida de Fourier . Si la forma de onda se crea digitalmente directamente en el dominio de tiempo utilizando una forma no limitada por banda , como y = x - floor (x), se muestrean infinitos armónicos y el tono resultante contiene distorsión de aliasing .

Animación de la síntesis aditiva de una onda de diente de sierra con un número creciente de armónicos.

Una demostración de audio de un diente de sierra reproducido a 440 Hz (A4) y 880 Hz (A5) y 1760 Hz (A6) está disponible a continuación. Se presentan los tonos de banda limitada (sin alias) y de alias.

Aplicaciones [ editar ]

• Las ondas de diente de sierra son conocidas por su uso en la música. El diente de sierra y ondas cuadradas son algunas de las formas de onda más comunes utilizados para crear sonidos con sustractivo analógico y analógico virtuales sintetizadores de música.
• Las ondas de diente de sierra se utilizan en las fuentes de alimentación de modo conmutado . En el chip regulador, la señal de realimentación de la salida se compara continuamente con un diente de sierra de alta frecuencia para generar una nueva señal PWM de ciclo de trabajo en la salida del comparador .
• La onda de diente de sierra es la forma de las señales de desviación vertical y horizontal que se utilizan para generar una trama en pantallas de televisión o monitores basadas en CRT . Los osciloscopios también usan una onda de diente de sierra para su deflexión horizontal, aunque típicamente usan la desviación electrostática .
• En la "rampa" de la onda, el campo magnético producido por el yugo de desviación arrastra el haz de electrones a través de la cara del CRT, creando una línea de exploración .
• En el "acantilado" de la onda, el campo magnético colapsa repentinamente, haciendo que el haz de electrones vuelva a su posición de reposo tan rápido como sea posible.
• La tensión aplicada al yugo de desviación se ajusta por varios medios (transformadores, condensadores, devanados de toma central) de manera que la tensión de medio camino en el acantilado del diente de sierra se encuentre en la marca cero, lo que significa que una tensión negativa causará la desviación en una dirección , y una desviación de tensión positiva en la otra; por lo tanto, un yugo de desviación montado en el centro puede utilizar toda el área de la pantalla para representar una traza. La frecuencia es 15.734 kHz en NTSC , 15.625 kHz para PAL y SECAM ).
• El sistema de deflexión vertical funciona de la misma manera que el horizontal, aunque a una frecuencia mucho más baja (59.94 Hz en NTSC , 50 Hz para PAL y SECAM).
• La porción de rampa de la onda debe aparecer como una línea recta. De lo contrario, indica que el voltaje no aumenta linealmente y, por lo tanto, que el campo magnético producido por el yugo de desviación no es lineal. Como resultado, el haz de electrones se acelerará durante las porciones no lineales. Esto daría lugar a una imagen de televisión "aplastada" en la dirección de la no linealidad. Los casos extremos mostrarán marcados aumentos de brillo, ya que el haz de electrones pasa más tiempo en ese lado de la imagen.
• Los primeros receptores de televisión tenían controles que permitían a los usuarios ajustar la linealidad vertical u horizontal de la imagen. Dichos controles no estaban presentes en series posteriores ya que la estabilidad de los componentes electrónicos había mejorado.

 la aproximación σ ajusta una suma de Fourier para reducir en gran medida el fenómeno de Gibbs , que de lo contrario ocurriría en las discontinuidades .

Una suma aproximada σ para una serie del período T se puede escribir de la siguiente manera:

$${\ displaystyle s (\ theta) = {\ frac {1} {2}} a_ {0} + \ sum _ {k = 1} ^ {m-1} \ operatorname {sinc} {\ frac {k} { m}} \ cdot \ left [a_ {k} \ cos \ left ({\ frac {2 \ pi k} {T}} \ theta \ right) + b_ {k} \ sin \ left ({\ frac {2 \ pi k} {T}} \ theta \ right) \ right],}

en términos de la función sinc normalizada

$${\ displaystyle \ operatorname {sinc} x = {\ frac {\ sin \ pi x} {\ pi x}}.}

El termino

$${\ displaystyle \ operatorname {sinc} {\ frac {k} {m}}}

es el factor σ de Lanczos , que es responsable de eliminar la mayor parte del fenómeno de Gibbs. Sin embargo, no lo hace completamente, pero se puede cuadrar o incluso combinar la expresión para atenuar en serie el fenómeno de Gibbs en los casos más extremos.

 onda cuadrada es una forma de onda periódica no sinusoidal en la que la amplitud se alterna a una frecuencia constante entre los valores mínimo y máximo fijos, con la misma duración como mínimo y como máximo. Aunque no es realizable en sistemas físicos, la transición entre mínimo y máximo es instantánea para una onda cuadrada ideal.

La onda cuadrada es un caso especial de una onda de pulso que permite duraciones arbitrarias como mínimo y máximo. La relación del período alto al período total de una onda de pulso se denomina ciclo de trabajo . Una onda cuadrada verdadera tiene un ciclo de trabajo del 50% (períodos altos y bajos iguales).

Las ondas cuadradas se encuentran a menudo en la electrónica y procesamiento de señales . Su contraparte estocástica es una trayectoria de dos estados .

Formas de onda sinusoidales , cuadradas, triangulares y de diente de sierra.

Origen y usos [ editar ]

Las ondas cuadradas se encuentran universalmente en los circuitos de conmutación digital y se generan naturalmente mediante dispositivos lógicos binarios (dos niveles). Se utilizan como referencias de temporización o " señales de reloj ", porque sus transiciones rápidas son adecuadas para disparar circuitos lógicos síncronos en intervalos determinados con precisión. Sin embargo, como muestra el gráfico del dominio de la frecuencia, las ondas cuadradas contienen una amplia gama de armónicos; Estos pueden generar radiación electromagnética o pulsos de corriente que interfieren con otros circuitos cercanos, causando ruido o errores. Para evitar este problema en circuitos muy sensibles, como los convertidores de analógico a digital de precisión , las ondas sinusoidales Se utilizan en lugar de las ondas cuadradas como referencias de tiempo.

En términos musicales, a menudo se los describe como sonoros huecos y, por lo tanto, se utilizan como base para los sonidos de instrumentos de viento creados mediante síntesis sustractiva . Además, el efecto de distorsión utilizado en las guitarras eléctricas recorta las regiones más externas de la forma de onda, lo que hace que se parezca cada vez más a una onda cuadrada a medida que se aplica más distorsión.

Las funciones simples de dos niveles de Rademacher son ondas cuadradas.

Definiciones [ editar ]

La onda cuadrada en matemáticas tiene muchas definiciones, que son equivalentes excepto en las discontinuidades:

Se puede definir como simplemente la función de signo de una sinusoide:

{\ displaystyle {\ begin {alineado} x (t) & = \ operatorname {sgn} \ left (\ sin {\ frac {2 \ pi t} {T}} \ right) = \ operatorname {sgn} (\ sin 2 \ pi ft) \\ v (t) & = \ operatorname {sgn} \ left (\ cos {\ frac {2 \ pi t} {T}} \ right) = \ operatorname {sgn} (\ cos 2 \ pi ft), \ end {alineado}}}

que será 1 cuando la sinusoide sea positiva, −1 cuando la sinusoide sea negativa y 0 en las discontinuidades. Aquí, T es el período de la onda cuadrada, o de manera equivalente, f es su frecuencia, donde f = 1 / T .

También se puede definir una onda cuadrada con respecto a la función de escalón de Heaviside u ( t ) o la función rectangular ( t ):

{\ displaystyle {\ begin {alineado} x (t) & = 2 \ left [\ sum _ {n = - \ infty} ^ {\ infty} \ Pi \ left ({\ frac {2 (t-nT)} {T}} - {\ frac {1} {2}} \ derecha) \ derecha] -1 \\ & = 2 \ suma _ {n = - \ infty} ^ {\ infty} \ izquierda [u \ izquierda ( {\ frac {t} {T}} - n \ derecha) -u \ izquierda ({\ frac {t} {T}} - n - {\ frac {1} {2}} \ derecha) \ derecha] - 1. \ end {alineado}}}

También se puede generar una onda cuadrada usando la función de piso directamente:

$${\ displaystyle x (t) = 2 \ left (2 \ lfloor ft \ rfloor - \ lfloor 2ft \ rfloor \ right) +1}

e indirectamente:

$${\ displaystyle x (t) = \ left (-1 \ right) ^ {\ lfloor ft \ rfloor}.}

análisis de Fourier [ editar ]

Las seis flechas representan los primeros seis términos de la serie de Fourier de una onda cuadrada. Los dos círculos en la parte inferior representan la onda cuadrada exacta (azul) y su aproximación de la serie de Fourier (púrpura).

Armónicos (impares) de una onda cuadrada de 1000 Hz

Gráfico que muestra los primeros 3 términos de la serie de Fourier de una onda cuadrada

Usando la expansión de Fourier con la frecuencia de ciclo fen el tiempo t , una onda cuadrada ideal con una amplitud de 1 se puede representar como una suma infinita de ondas sinusoidales:

{\ displaystyle {\ begin {alineado} x (t) & = {\ frac {4} {\ pi}} \ sum _ {k = 1} ^ {\ infty} {\ frac {\ sin \ left (2 \ pi (2k-1) ft \ right)} {2k-1}} \\ & = {\ frac {4} {\ pi}} \ left (\ sin (\ omega t) + {\ frac {1} { 3}} \ sin (3 \ omega t) + {\ frac {1} {5}} \ sin (5 \ omega t) + \ ldots \ right), & {\ text {where}} \ omega = 2 \ pi f \ end {alineado}}}

	Demostración cuadrada aditiva MENÚ 0:00 Onda cuadrada de 220 Hz creada por armónicos agregados cada segundo sobre la onda sinusoidal
¿Problemas para reproducir este archivo? Ver la ayuda de los medios .

La onda cuadrada ideal contiene solo componentes de frecuencias armónicas de números impares (de la forma 2π (2 k - 1) f ). Las ondas de diente de sierra y las señales del mundo real contienen todos los armónicos enteros.

Una curiosidad de la convergencia de la representación de la onda cuadrada de la serie de Fourier es el fenómeno de Gibbs . Se puede demostrar que los artefactos de timbre en ondas cuadradas no ideales están relacionados con este fenómeno. El fenómeno de Gibbs se puede prevenir mediante el uso de la aproximación σ , que utiliza los factores de sigma de Lanczos para ayudar a que la secuencia converja más suavemente.

Una onda cuadrada matemática ideal cambia instantáneamente entre el estado alto y el estado bajo y sin disparar ni disparar. Esto es imposible de lograr en los sistemas físicos, ya que requeriría un ancho de bandainfinito .

Animación de la síntesis aditiva de una onda cuadrada con un número creciente de armónicos.

Las ondas cuadradas en los sistemas físicos solo tienen un ancho de banda finito y, a menudo, muestran efectos de timbre similares a los del fenómeno de Gibbs o efectos de onda similares a los de la aproximación σ.

Para una aproximación razonable a la forma de onda cuadrada, al menos el fundamental y el tercer armónico deben estar presentes, siendo deseable el quinto armónico. Estos requisitos de ancho de banda son importantes en la electrónica digital, donde se utilizan aproximaciones analógicas de ancho de banda finito a formas de onda de forma de onda cuadrada. (Los transitorios de timbre son una consideración electrónica importante aquí, ya que pueden ir más allá de los límites de clasificación eléctrica de un circuito o hacer que un umbral mal posicionado se cruce varias veces).

	Muestra sonora de onda cuadrada MENÚ 0:00 5 segundos de onda cuadrada a 1 kHz
¿Problemas para reproducir este archivo? Ver la ayuda de los medios .

Características de las ondas cuadradas imperfectos [ editar ]

Como ya se mencionó, una onda cuadrada ideal tiene transiciones instantáneas entre los niveles alto y bajo. En la práctica, esto nunca se logra debido a las limitaciones físicas del sistema que genera la forma de onda. Los tiempos tomados para que la señal aumente del nivel bajo al nivel alto y viceversa se denominan tiempo de subida y tiempo de caída respectivamente.

Si el sistema está sobrecalentado , entonces la forma de onda nunca alcanzará realmente los niveles teóricos alto y bajo, y si el sistema está mal amortiguado, oscilará alrededor de los niveles alto y bajo antes de establecerse. En estos casos, los tiempos de aumento y caída se miden entre niveles intermedios especificados, como 5% y 95%, o 10% y 90%. El ancho de banda de un sistema está relacionado con los tiempos de transición de la forma de onda; Hay fórmulas que permiten que una sea determinada aproximadamente de la otra.