SERIES MATEMÁTICAS

núcleo de sumabilidad es una familia o secuencia de funciones integrables periódicas que satisfacen un determinado conjunto de propiedades, que se enumeran a continuación. Ciertos núcleos, como el núcleo Fejér , son particularmente útiles en el análisis de Fourier . Los núcleos de sumabilidad están relacionados con la aproximación de la identidad ; las definiciones de una aproximación de identidad varían, ^[1]pero a veces la definición de una aproximación de la identidad se considera la misma que para un núcleo de sumabilidad.

Definición [ editar ]

Dejar $${\ displaystyle \ mathbb {T}: = \ mathbb {R} / \ mathbb {Z}}. Un kernel de sumabilidad es una secuencia.$${\ displaystyle (k_ {n})} en $${\ displaystyle L ^ {1} (\ mathbb {T})} que satisface

1. $${\ displaystyle \ int _ {\ mathbb {T}} k_ {n} (t) \, dt = 1}
2. $${\ displaystyle \ int _ {\ mathbb {T}} | k_ {n} (t) | \, dt \ leq M} (uniformemente delimitado)
3. $${\ displaystyle \ int _ {\ delta \ leq | t | \ leq {\ frac {1} {2}}} | k_ {n} (t) | \, dt \ to 0} como $${\ displaystyle n \ to \ infty}, para cada {\ displaystyle \ delta> 0}.

Tenga en cuenta que si $${\ displaystyle k_ {n} \ geq 0} para todos $${\ displaystyle n}es decir $${\ displaystyle (k_ {n})}es un núcleo de suma positiva , entonces el segundo requisito sigue automáticamente al primero.

Si por el contrario tomamos la convención. $${\ displaystyle \ mathbb {T} = \ mathbb {R} / 2 \ pi \ mathbb {Z}}, la primera ecuación se convierte en $${\ displaystyle {\ frac {1} {2 \ pi}} \ int _ {\ mathbb {T}} k_ {n} (t) \, dt = 1}, y el límite superior de integración en la tercera ecuación debe extenderse a $${\ displaystyle \ pi}.

También podemos considerar $${\ displaystyle \ mathbb {R}} más bien que $${\ displaystyle \ mathbb {T}}; luego integramos (1) y (2) sobre$${\ displaystyle \ mathbb {R}}, y (3) sobre {\ displaystyle | t |> \ delta}.

Ejemplos [ editar ]

• El núcleo de Fejér
• El núcleo de Poisson (índice continuo)
• El kernel de Dirichlet no es un kernel de suma, ya que no cumple con el segundo requisito.

Convoluciones [ editar ]

Dejar $${\ displaystyle (k_ {n})} ser un núcleo de sumerabilidad, y $${\ displaystyle *}denota la operación de convolución .

• Si $${\ displaystyle (k_ {n}), f \ in {\ mathcal {C}} (\ mathbb {T})} (funciones continuas en $${\ displaystyle \ mathbb {T}}), entonces $${\ displaystyle k_ {n} * f \ to f} en $${\ displaystyle {\ mathcal {C}} (\ mathbb {T})}, es decir, uniformemente, como $${\ displaystyle n \ to \ infty}.
• Si $${\ displaystyle (k_ {n}), f \ en L ^ {1} (\ mathbb {T})}, entonces $${\ displaystyle k_ {n} * f \ to f} en $${\ displaystyle L ^ {1} (\ mathbb {T})}, como $${\ displaystyle n \ to \ infty}.
• Si $${\ displaystyle (k_ {n})} está disminuyendo radialmente simétrica y $${\ displaystyle f \ en L ^ {1} (\ mathbb {T})}, entonces $${\ displaystyle k_ {n} * f \ to f} puntualmente ae , como$${\ displaystyle n \ to \ infty}. Esto utiliza la función máxima de Hardy-Littlewood . Si$${\ displaystyle (k_ {n})} no está disminuyendo radialmente la simetría, sino la disminución de la simetrización $${\ displaystyle {\ widetilde {k}} _ {n} (x): = \ sup _ {| y | \ geq | x |} k_ {n} (y)} satisface {\ displaystyle \ sup _ {n \ in \ mathbb {N}} \ | {\ widetilde {k_ {n}}} \ | _ {1} <\ infty}, entonces una convergencia todavía se mantiene, utilizando un argumento similar.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una onda triangular con límite de banda representada en el dominio del tiempo (superior) y el dominio de la frecuencia (inferior). Lo fundamental es a 220 Hz (A3).

	Muestra sonora de onda triangular MENÚ 0:00 5 segundos de onda triangular a 220 Hz
¿Problemas para reproducir este archivo? Ver la ayuda de los medios .

	Muestra aditiva de la onda del triángulo MENU 0:00 Después de cada segundo, se agrega una armónica a una onda sinusoidal creando una onda triangular de 220 Hz.
¿Problemas para reproducir este archivo? Ver la ayuda de los medios .

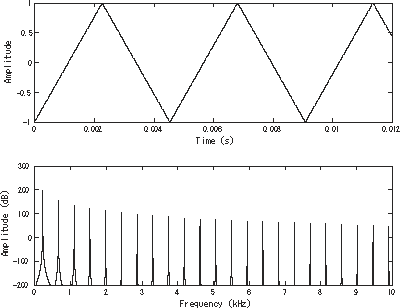
Una onda triangular es una forma de onda no sinusoidal llamada así por su forma triangular . Es una función real continua , periódica , por partes lineales .

Como una onda cuadrada , la onda triangular contiene solo armónicos impares . Sin embargo, los armónicos superiores se desprenden mucho más rápido que en una onda cuadrada (proporcional al cuadrado inverso del número armónico, en oposición a la inversa).

Armónicos [ editar ]

Animación de la síntesis aditiva de una onda triangular con un número creciente de armónicos. Ver análisis de Fourierpara una descripción matemática.

Es posible aproximar una onda triangular con síntesis aditivasumando armónicos impares de la fundamental mientras se multiplican todos los armónicos impares por −1 (o, equivalentemente, cambiando su fase por π) y multiplicando la amplitud de los armónicos por uno sobre el cuadrado de su número de modo, n , (que es equivalente a uno sobre el cuadrado de su frecuencia relativa a la fundamental ).

Lo anterior se puede resumir matemáticamente de la siguiente manera:

{\ displaystyle {\ begin {alineado} x _ {\ mathrm {triangle}} (t) & {} = {\ frac {\ pi} {4}} \ sum _ {i = 0} ^ {N} (- 1 ) ^ {i} n ^ {- 2} \ left (\ sin [nt] \ right) \ end {alineado}}}

donde N es el número de armónicos a incluir en la aproximación, t es la variable independiente (por ejemplo, el tiempo para las ondas de sonido) ei es la etiqueta armónica que está relacionada con su número de modo por$${\ displaystyle n = 2i + 1}.

Esta serie infinita de Fourier converge a la onda triangular ya que N tiende a infinito, como se muestra en la animación.

Definiciones [ editar ]

Formas de onda sinusoidales , cuadradas , triangulares y de diente de sierra.

Otra definición de la onda triangular, con un rango de -1 a 1 y período $${\ displaystyle p,} es:

$${\ displaystyle x (t) = {\ frac {4} {p}} \ left (t - {\ frac {p} {2}} \ left \ lfloor {\ frac {2t} {p}} + {\ frac {1} {2}} \ right \ rfloor \ right) (- 1) ^ {\ left \ lfloor {\ frac {2t} {p}} + {\ frac {1} {2}} \ right \ rfloor }}

donde el simbolo $${\ displaystyle \ lfloor n \ rfloor}es la función de piso de n .

Además, la onda triangular puede ser el valor absoluto de la onda de diente de sierra :

$${\ displaystyle x (t) = 2 \ left | {t \ over p} - \ left \ lfloor {t \ over p} + {1 \ over 2} \ right \ rfloor \ right |}

o, para un rango de -1 a +1:

$${\ displaystyle x (t) = 2 \ left | 2 \ left ({t \ over p} - \ left \ lfloor {t \ over p} + {1 \ over 2} \ right \ rfloor \ right) \ right | -1.}

La onda triangular también se puede expresar como la integral de la onda cuadrada :

$${\ displaystyle x (t) = \ int _ {0} ^ {t} \ operatorname {sgn} (\ sin (u)) \, du.}

Aquí hay una ecuación simple con un período de 4 y un valor inicial $${\ displaystyle y (0) = 1}:

$${\ displaystyle y (x) = | x \, {\ bmod {\,}} 4-2 | -1.}

Como esto solo utiliza la operación de módulo y el valor absoluto , se puede usar para implementar simplemente una onda triangular en la electrónica del hardware con menos potencia de la CPU. La ecuación anterior se puede generalizar por un período de$${\ displaystyle p,} amplitud $${\ displaystyle a,} y valor inicial $${\ displaystyle y (0) = a / 2}:

$${\ displaystyle y (x) = {\ frac {2a} {p}} {\ biggl |} \ left (x {\ bmod {p}} \ right) - {\ frac {p} {2}} {\ biggr |} - {\ frac {2a} {4}}.}

La primera función es una especialización de la segunda para a = 2 yp = 4:

$${\ displaystyle y (x) = {\ frac {2 \ times 2} {4}} {\ biggl |} \ left (x {\ bmod {4}} \ right) - {\ frac {4} {2} } {\ biggr |} - {\ frac {2 \ times 2} {4}} \ Leftrightarrow}

$${\ displaystyle y (x) = | \ left (x {\ bmod {4}} \ right) -2 | -1.}

Se puede hacer una versión impar de la primera función, simplemente cambiando en uno el valor de entrada, lo que cambiará la fase de la función original:

$${\ displaystyle y (x) = | (x-1) \, {\ bmod {\,}} 4-2 | -1.}

Generalizando esto para que la función sea impar para cualquier período y amplitud da:

$${\ displaystyle y (x) = {\ frac {4a} {p}} {\ biggl |} \ left ((x - {\ frac {p} {4}}) {\ bmod {p}} \ right) - {\ frac {p} {2}} {\ biggr |} -a.}

En términos de seno y arcoseno con periodo p y amplitud a :

$${\ displaystyle y (x) = {\ frac {2a} {\ pi}} \ arcsin \ left (\ sin \ left ({\ frac {2 \ pi} {p}} x \ right) \ right).}

Longitud del arco [ editar ]

La longitud del arco por período "s" para una onda triangular, dada la amplitud "a" y la duración del período "p":

$${\ displaystyle s = {\ sqrt {(4a) ^ {2} + p ^ {2}}}.}