prueba de convergencia de Cauchy es un método utilizado para probar serie infinita de convergencia . Se basa en la suma de los términos de la serie. Este criterio de convergencia lleva el nombre de Augustin-Louis Cauchy, quien lo publicó en su libro de texto Cours d'Analyse 1821.
Declaración [ editar ]
Una serie
- es convergente si y solo si para cada Hay un número natural N tal que
Explicación [ editar ]
La prueba funciona porque el espacio R de los números reales y el espacio C de los números complejos (con la métrica dada por el valor absoluto) están ambos completos . Entonces la serie es convergente si y solo si la suma parcial
Una secuencia de números reales o complejos. es una secuencia de Cauchy si y solo si converge (hasta cierto punto a en R o C ). [3] La definición formal establece que para cadahay un número N , tal que para todos n , m > N se mantiene
Asumiremos m > n y, por lo tanto, estableceremos p = m - n .
Mostrar que una secuencia es una secuencia de Cauchy es útil, ya que no necesitamos conocer el límite de la secuencia en cuestión. La prueba de convergencia de Cauchy solo se puede utilizar en espacios métricos completos (como R y C ), que son espacios donde convergen todas las secuencias de Cauchy. Solo necesitamos mostrar que sus elementos se vuelven arbitrariamente cercanos entre sí después de una progresión finita en la secuencia. Existen aplicaciones informáticas de la secuencia de Cauchy, en las que se puede configurar un proceso iterativo para crear tales secuencias.
Prueba [ editar ]
Podemos usar los resultados sobre la convergencia de la secuencia de sumas parciales de las series infinitas y aplicarlas a la convergencia de las mismas series infinitas. La prueba de criterio de Cauchy es una de esas aplicaciones. Para cualquier secuencia real., los resultados anteriores sobre convergencia implican que las series infinitas
m ≥ n ≥ N implica
Probablemente la parte más interesante de [este teorema] es que la condición de Cauchy implica la existencia del límite: esto está relacionado con la integridad de la línea real. El criterio de Cauchy se puede generalizar a una variedad de situaciones, que se pueden resumir a la ligera como "una condición de oscilación que desaparece es equivalente a la convergencia". [5]
Este artículo incorpora material del criterio de Cauchy para la convergencia en PlanetMath , que está licenciado bajo la licencia Creative Commons Attribution / Share-Alike .
pruebas de Dini y Dini-Lipschitz son pruebas altamente precisas que pueden usarse para probar que la serie de Fourier de una función converge en un punto determinado. Estas pruebas llevan el nombre de Ulisse Dini y Rudolf Lipschitz .
Definición [ editar ]
Sea f una función en [0,2 π ], t sea algún punto y δ sea un número positivo. Definimos el módulo de continuidad local en el punto t por
Tenga en cuenta que aquí consideramos que f es una función periódica, por ejemplo, si t = 0 y ε es negativo, definimos f ( ε ) = f (2π + ε ) .
Con estas definiciones podemos indicar los principales resultados:
- Teorema (prueba de Dini): Supongamos que una función f satisface en un punto t que
- Entonces la serie de Fourier de f converge de t a f ( t ) .
Por ejemplo, el teorema se mantiene con ω f = log −2 ( 1δ ) pero no se mantiene con log −1 ( 1δ ) .
- Teorema (la prueba de Dini-Lipschitz): Supongamos que una función f satisface
- Entonces la serie de Fourier de f converge uniformemente a f .
En particular, cualquier función de una clase de Hölder [ aclaración necesaria ] satisface la prueba de Dini-Lipschitz.
Precisión [ editar ]
Ambas pruebas son las mejores de su tipo. Para la prueba Dini-Lipschitz, es posible construir una función f con su módulo de continuidad que satisfaga la prueba con O en lugar de o , es decir
y la serie de Fourier de f diverges. Para la prueba de Dini, la declaración de precisión es ligeramente más larga: dice que para cualquier función Ω tal que
existe una función f tal que
y la serie de Fourier de f diverge en 0.
prueba de comparación , a veces llamada prueba de comparación directa para distinguirla de pruebas relacionadas similares (especialmente la prueba de comparación límite ), proporciona una forma de deducir la convergencia o divergencia de una serie infinita o una integral inadecuada . En ambos casos, la prueba funciona comparando la serie dada o la integral con una cuyas propiedades de convergencia son conocidas.
Para series [ editar ]
En el cálculo , la prueba de comparación para series generalmente consiste en un par de declaraciones sobre series infinitas con términos no negativos (valor real ): [1]
- Si la serie infinita converge y para todos suficientemente grande n (es decir, para todospara algún valor fijo N ), entonces la serie infinita También converge.
- Si la serie infinita diverges y para todos los suficientemente grandes n , entonces la serie infinita también diverge.
Tenga en cuenta que a veces se dice que las series que tienen términos más grandes dominan (o eventualmente dominan ) las series con términos más pequeños. [2]
Alternativamente, la prueba puede establecerse en términos de convergencia absoluta , en cuyo caso también se aplica a series con términos complejos : [3]
- Si la serie infinita es absolutamente convergente y para todos los suficientemente grandes n , entonces la serie infinita También es absolutamente convergente.
- Si la serie infinita no es absolutamente convergente y para todos los suficientemente grandes n , entonces la serie infinita Tampoco es absolutamente convergente.
Tenga en cuenta que en esta última afirmación, la serie. Todavía podría ser condicionalmente convergente; para series de valor real, esto podría suceder si la a n no son todas negativas.
El segundo par de sentencias es equivalente al primero en el caso de series de valores reales porque converge absolutamente si y solo si , una serie con términos no negativos, converge.
Prueba [ editar ]
Las pruebas de todas las afirmaciones dadas anteriormente son similares. Aquí está una prueba de la tercera declaración.
Dejar y ser infinitas series tales que converge absolutamente (por lo tanto converge), y sin pérdida de generalidad suponemos quepara todos los enteros positivos n . Considera las sumas parciales
Ya que converge absolutamente, para algun numero real t . Para todo n ,
Es una secuencia no decreciente y no es intensificante Dado entonces ambos pertenecen al intervalo cuya longitud disminuye a cero como va al infinito. Esto muestra queEs una secuencia de Cauchy , por lo que debe converger a un límite. Por lo tanto, Es absolutamente convergente.
Para integrales [ editar ]
La prueba de comparación para integrales se puede establecer como sigue, asumiendo funciones continuas de valores reales f y g encon b tampocoo un número real en el que f y g tienen cada uno una asíntota vertical: [4]
- Si la integral impropia converge y para , entonces la integral impropia tambien converge con
- Si la integral impropia diverges y para , entonces la integral impropia también diverge.
Prueba de comparación de proporciones [ editar ]
Otra prueba para la convergencia de series de valores reales, similar tanto a la prueba de comparación directa anterior como a la prueba de relación , se llama prueba de comparación de relación : [5]
- Si la serie infinita converge y , y para todos los suficientemente grandes n , entonces la serie infinita También converge.
- Si la serie infinita diverges y , y para todos los suficientemente grandes n , entonces la serie infinita también diverge.



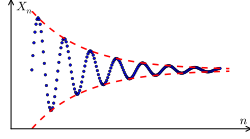


































![{\ displaystyle [S_ {N}, S_ {N} + (T-T_ {N})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d1773a744d47205d0634981245aaf506d3f3ca)















No hay comentarios:
Publicar un comentario