SERIES DE FOURIER , CONTINUACIÓN
| " | 
Multiplicando ambos lados por  , y luego integrando desde , y luego integrando desde  a a  rendimientos rendimientos

| ” |
| - Joseph Fourier, Mémico sobre la propagación del chaleur dans les corps solides . (1807) [12] [nb 3] |
Esto da inmediatamente cualquier coeficiente de un k de la serie trigonométrica para φ ( y ) para cualquier función que tiene tal expansión. Funciona porque si φ tiene tal expansión, entonces (bajo supuestos de convergencia adecuados) la integral

Puede llevarse a cabo término por término. Pero todos los términos que involucran para j ≠ k desaparece cuando se integra de −1 a 1, dejando solo el término kth.
para j ≠ k desaparece cuando se integra de −1 a 1, dejando solo el término kth.
En estas pocas líneas, que están cerca del formalismo moderno utilizado en las series de Fourier, Fourier revolucionó tanto las matemáticas como la física. Aunque Euler , D'Alembert , Daniel Bernoulli y Gauss utilizaron series trigonométricas similares , Fourier creía que tales series trigonométricas podrían representar cualquier función arbitraria. En qué sentido, en realidad, es un tema un tanto sutil y los intentos durante muchos años de aclarar esta idea han llevado a importantes descubrimientos en las teorías de la convergencia , los espacios funcionales y el análisis armónico .
Cuando Fourier presentó un ensayo posterior sobre la competencia en 1811, el comité (que incluía a Lagrange , Laplace , Malus y Legendre , entre otros) concluyó: ... la forma en que el autor llega a estas ecuaciones no está exenta de dificultades y ... Su análisis para integrarlos aún deja algo que desear en la generalidad e incluso en el rigor . [ cita requerida ]
Nacimiento de análisis armónico [ editar ]
Desde la época de Fourier, se han descubierto muchos enfoques diferentes para definir y comprender el concepto de series de Fourier, todos los cuales son coherentes entre sí, pero cada uno de ellos enfatiza diferentes aspectos del tema. Algunos de los enfoques más potentes y elegantes se basan en ideas y herramientas matemáticas que no estaban disponibles cuando Fourier completó su trabajo original. Fourier definió originalmente la serie de Fourier para funciones de valores reales de argumentos reales, y el uso de las funciones de seno y coseno como la base para la descomposición.
Muchas otras transformaciones relacionadas con Fourier se han definido desde entonces, extendiendo la idea inicial a otras aplicaciones. Esta área general de investigación ahora se llama a veces análisis armónico . Sin embargo, una serie de Fourier se puede usar solo para funciones periódicas o para funciones en un intervalo limitado (compacto).
Extensiones [ editar ]
Series de Fourier en un cuadrado [ editar ]
También podemos definir la serie de Fourier para funciones de dos variables.  y
y  en la plaza
en la plaza ![{\ displaystyle [- \ pi, \ pi] \ times [- \ pi, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb) :
:
![{\ displaystyle {\ begin {alineado} f (x, y) & = \ sum _ {j, k \, \ in \, \ mathbb {Z} {\ text {(enteros)}}} c_ {j, k } e ^ {ijx} e ^ {iky}, \\ [5pt] c_ {j, k} & = {1 \ sobre 4 \ pi ^ {2}} \ int _ {- \ pi} ^ {\ pi} \ int _ {- \ pi} ^ {\ pi} f (x, y) e ^ {- ijx} e ^ {- iky} \, dx \, dy. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71f5aaa23f00684f16ecbf31838ff5ac61f807db)
Además de ser útil para resolver ecuaciones diferenciales parciales, como la ecuación de calor, una aplicación notable de las series de Fourier en el cuadrado es la compresión de imágenes . En particular, el estándar de compresión de imagen jpeg utiliza la transformada de coseno discreta bidimensional , que es una transformada de Fourier que utiliza las funciones de base de coseno.
Series de Fourier de función de Bravais-enrejado-periódico [ editar ]
La red tridimensional de Bravais se define como el conjunto de vectores de la forma:

dónde  son enteros y
son enteros y  Son tres vectores linealmente independientes. Suponiendo que tenemos alguna función,
Son tres vectores linealmente independientes. Suponiendo que tenemos alguna función, , de forma que cumpla con la siguiente condición para cualquier vector de celosía Bravais
, de forma que cumpla con la siguiente condición para cualquier vector de celosía Bravais  , podríamos hacer una serie de Fourier. Este tipo de función puede ser, por ejemplo, el potencial efectivo que un electrón "siente" dentro de un cristal periódico. Es útil hacer una serie de Fourier del potencial para aplicar el teorema de Bloch . Primero, podemos escribir cualquier vector arbitrario.
, podríamos hacer una serie de Fourier. Este tipo de función puede ser, por ejemplo, el potencial efectivo que un electrón "siente" dentro de un cristal periódico. Es útil hacer una serie de Fourier del potencial para aplicar el teorema de Bloch . Primero, podemos escribir cualquier vector arbitrario. en el sistema de coordenadas de la red:
en el sistema de coordenadas de la red:

dónde 
Así podemos definir una nueva función,

Esta nueva función,  , ahora es una función de tres variables, cada una de las cuales tiene periodicidad a 1 , a 2 , a 3 respectivamente:
, ahora es una función de tres variables, cada una de las cuales tiene periodicidad a 1 , a 2 , a 3 respectivamente:

Si escribimos una serie para g en el intervalo [0, a 1 ] para x 1 , podemos definir lo siguiente:

Y luego podemos escribir:

Además de definir:
![\ begin {align} h ^ \ mathrm {two} (m_1, m_2, x_3) &: = \ frac {1} {a_2} \ int_0 ^ {a_2} h ^ \ mathrm {one} (m_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ frac {m_2} {a_2} x_2} \, dx_2 \\ [12pt] & = \ frac {1} {a_2} \ int_0 ^ {a_2} dx_2 \ frac {1} {a_1} \ int_0 ^ {a_1} dx_1 g (x_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ left (\ frac {m_1} {a_1} x_1 + \ frac {m_2} {a_2} x_2 \ derecha)} \ end {alinear}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)
Podemos escribir  una vez más como
una vez más como

Finalmente aplicando lo mismo para la tercera coordenada, definimos:
![\ begin {align} h ^ \ mathrm {three} (m_1, m_2, m_3) &: = frac {1} {a_3} \ int_0 ^ {a_3} h ^ \ mathrm {two} (m_1, m_2, x_3) \ cdot e ^ {- i 2 \ pi \ frac {m_3} {a_3} x_3} \, dx_3 \\ [12pt] & = \ frac {1} {a_3} \ int_0 ^ {a_3} dx_3 \ frac {1} {a_2} \ int_0 ^ {a_2} dx_2 \ frac {1} {a_1} \ int_0 ^ {a_1} dx_1 g (x_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ left (\ frac {m_1 } {a_1} x_1 + \ frac {m_2} {a_2} x_2 + \ frac {m_3} {a_3} x_3 \ right)} \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)
Nosotros escribimos  como:
como:

Reorganizar:

Ahora, cada vector de red recíproca puede escribirse como , dónde
, dónde  son enteros y
son enteros y  son los vectores de red recíproca, podemos usar el hecho de que
son los vectores de red recíproca, podemos usar el hecho de que  para calcular que para cualquier vector de red recíproca arbitraria
para calcular que para cualquier vector de red recíproca arbitraria  y vector arbitrario en el espacio.
y vector arbitrario en el espacio.  , su producto escalar es:
, su producto escalar es:

Y así queda claro que en nuestra expansión, la suma es en realidad sobre vectores de red recíproca:

dónde

Asumiendo

Podemos resolver este sistema de tres ecuaciones lineales para  ,
,  y
y  en términos de
en términos de  ,
,  y
y  para calcular el elemento de volumen en el sistema de coordenadas cartesiano original. Una vez que tengamos
para calcular el elemento de volumen en el sistema de coordenadas cartesiano original. Una vez que tengamos ,
,  y
y  en términos de
en términos de  ,
,  y
y  , podemos calcular el determinante jacobiano :
, podemos calcular el determinante jacobiano :
![{\ displaystyle {\ begin {vmatrix} {\ dfrac {\ parcial x_ {1}} {\ parcial x}} & {\ dfrac {\ parcial x_ {1}} {\ parcial y}} & {\ dfrac {\ parcial x_ {1}} {\ parcial z}} \\ [12pt] {\ dfrac {\ parcial x_ {2}} {\ parcial x}} & {\ dfrac {\ parcial x_ {2}} {\ parcial y }} & {\ dfrac {\ parcial x_ {2}} {\ parcial z}} \\ [12pt] {\ dfrac {\ parcial x_ {3}} {\ parcial x}} & {\ dfrac {\ parcial x_ {3}} {\ parcial y}} & {\ dfrac {\ parcial x_ {3}} {\ parcial z}} \ fin {vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)
que después de algún cálculo y aplicación de algunas identidades de productos cruzados no triviales se puede demostrar que es igual a:

(Puede ser ventajoso para simplificar los cálculos, trabajar en un sistema de coordenadas cartesiano de este tipo, en el que sucede que  es paralelo al eje x,
es paralelo al eje x,  se encuentra en el plano x - y , y
se encuentra en el plano x - y , y tiene componentes de los tres ejes). El denominador es exactamente el volumen de la celda unitaria primitiva que está encerrada por los tres vectores primitivos
tiene componentes de los tres ejes). El denominador es exactamente el volumen de la celda unitaria primitiva que está encerrada por los tres vectores primitivos ,
,  y
y  . En particular, ahora sabemos que
. En particular, ahora sabemos que

Podemos escribir ahora  como una integral con el sistema de coordenadas tradicional sobre el volumen de la celda primitiva, en lugar de con el
como una integral con el sistema de coordenadas tradicional sobre el volumen de la celda primitiva, en lugar de con el  ,
,  y
y  variables:
variables:

Y  Es la célula unitaria primitiva, por lo tanto,
Es la célula unitaria primitiva, por lo tanto,  Es el volumen de la célula unidad primitiva.
Es el volumen de la célula unidad primitiva.
Hilbert interpretación del espacio [ editar ]
En el lenguaje de los espacios de Hilbert , el conjunto de funciones. Es una base ortonormal para el espacio.
Es una base ortonormal para el espacio.![{\ displaystyle L ^ {2} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) de funciones cuadrado-integrables en
de funciones cuadrado-integrables en ![[- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) . Este espacio es en realidad un espacio de Hilbert con un producto interno dado para cualquiera de los dos elementos.
. Este espacio es en realidad un espacio de Hilbert con un producto interno dado para cualquiera de los dos elementos. y
y  por
por

El resultado básico de la serie de Fourier para los espacios de Hilbert se puede escribir como


Los senos y cosenos forman un conjunto ortonormal, como se ilustra arriba. La integral de seno, coseno y su producto es cero (las áreas verde y roja son iguales, y se cancelan) cuando ,
,  o las funciones son diferentes, y pi solo si
o las funciones son diferentes, y pi solo si  y
y  Son iguales, y la función utilizada es la misma.
Son iguales, y la función utilizada es la misma.
Esto corresponde exactamente a la compleja formulación exponencial dada anteriormente. La versión con senos y cosenos también se justifica con la interpretación del espacio de Hilbert. De hecho, los senos y cosenos forman un conjunto ortogonal :



Además, los senos y cosenos son ortogonales a la función constante.  . Una base ortonormal para
. Una base ortonormal para![{\ displaystyle L ^ {2} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) consistente en funciones reales está formado por las funciones
consistente en funciones reales está formado por las funciones  y
y  ,
,  con n = 1, 2, ... La densidad de su envergadura es una consecuencia del teorema de Stone-Weierstrass , pero también se desprende de las propiedades de los núcleos clásicos como el núcleo de Fejér .
con n = 1, 2, ... La densidad de su envergadura es una consecuencia del teorema de Stone-Weierstrass , pero también se desprende de las propiedades de los núcleos clásicos como el núcleo de Fejér .
Propiedades [ editar ]
Tabla de propiedades básicas [ editar ]
Esta tabla muestra algunas operaciones matemáticas en el dominio del tiempo y el efecto correspondiente en los coeficientes de la serie de Fourier. Notación:
 es el complejo conjugado de
es el complejo conjugado de .
. designado
designado  - Funciones periodicas definidas en.
- Funciones periodicas definidas en.  .
.![{\ displaystyle F [n], G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e397cb4324837020cdcdf1d32bb9f00e3bacc3) Designar los coeficientes de la serie de Fourier (forma exponencial) de
Designar los coeficientes de la serie de Fourier (forma exponencial) de  y
y  como se define en la ecuación Eq.5 .
como se define en la ecuación Eq.5 .
| Propiedad | Dominio del tiempo | Dominio de frecuencia (forma exponencial) | Observaciones | Referencia |
|---|
| Linealidad |  | ![{\ displaystyle a \ cdot F [n] + b \ cdot G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc955a6cf808d4921d875ff75eb9a0ef841fecc9) | números complejos  | |
| Inversión de tiempo / inversión de frecuencia |  | ![{\ displaystyle F [-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b4a4823263d9c8be71e81b434efa1e0e7f7b78) | | [13] : p. 610 |
| Conjugación del tiempo |  | ![{\ displaystyle F [-n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0bb8e1ac85b41420733bbc3176752128cb2ad1) | | [13] : p. 610 |
| Inversión de tiempo y conjugación |  | ![{\ displaystyle F [n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a49c30283e8c78c1a9bedb82bc10d910060b88d) | | |
| Parte real en el tiempo |  | ![{\ displaystyle {\ frac {1} {2}} (F [n] + F [-n] ^ {*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561b550cd40e3a9b9094047184114aa358f1a96b) | | |
| Parte imaginaria en el tiempo |  | ![{\ displaystyle {\ frac {1} {2i}} (F [n] -F [-n] ^ {*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2317f4fc3c68ae6247b484faefb4afcfb05dfbb) | | |
| Parte real en frecuencia |  | ![{\ displaystyle \ operatorname {Re} {(F [n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46139e55f1d3fefaedc2c50c143c2070a71cdb80) | | |
| Parte imaginaria en frecuencia. |  | ![{\ displaystyle \ operatorname {Im} {(F [n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b17cae376b2d16a948caa8532ba478bc7b78dbf) | | |
| Cambio de tiempo / modulación en frecuencia |  | ![{\ displaystyle F [n] \ cdot e ^ {- i {\ frac {2 \ pi x_ {0}} {T}} n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867072969dbc9aa6f27cca71a9ffeb6a6853a75) | Número Real  | [13] : p. 610 |
| Cambio de frecuencia / modulación en el tiempo. |  | ![{\ displaystyle F [n-n_ {0}] \!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ff33ce94b62cdac1424cda391a7a63d678bb78) | entero  | [13] : p. 610 |
Propiedades de simetría [ editar ]
Cuando las partes reales e imaginarias de una función compleja se descomponen en sus partes pares e impares, hay cuatro componentes, indicados a continuación por los subíndices RE, RO, IE y IO. Y hay un mapeo uno a uno entre los cuatro componentes de una función de tiempo complejo y los cuatro componentes de su compleja transformación de frecuencia : [14]

A partir de esto, varias relaciones son evidentes, por ejemplo :
- La transformación de una función de valores reales ( f RE + f RO ) es la función simétrica par F RE + i F IO . A la inversa, una transformación incluso simétrica implica un dominio de tiempo con valores reales.
- La transformación de una función de valor imaginario ( i f IE + i f IO ) es la función simétrica impar F RO + i F IE , y lo contrario es cierto.
- La transformación de una función de simetría par ( f RE + i f IO ) es la función de valor real F RE + F RO , y lo contrario es cierto.
- La transformación de una función simétrica impar ( f RO + i f IE ) es la función de valor imaginario i F IE + i F IO , y lo contrario es cierto.
Riemann-Lebesgue lemma [ editar ]
Si  es integrable ,
es integrable , ,
,  y
y  Este resultado se conoce como el lema de Riemann-Lebesgue .
Este resultado se conoce como el lema de Riemann-Lebesgue .
Propiedad derivada [ editar ]
Nosotros decimos eso  pertenece a
pertenece a  Si
Si  es una función periódica 2 π en
es una función periódica 2 π en cual es
cual es  Tiempos diferenciables, y su k ª derivada es continua.
Tiempos diferenciables, y su k ª derivada es continua.
- Si
 , entonces los coeficientes de Fourier
, entonces los coeficientes de Fourier  de la derivada
de la derivada  Se puede expresar en términos de los coeficientes de Fourier.
Se puede expresar en términos de los coeficientes de Fourier.  de la función
de la función  , a través de la fórmula
, a través de la fórmula  .
.
- Si
 , entonces
, entonces  . En particular, ya que
. En particular, ya que tiende a cero, tenemos que
tiende a cero, tenemos que  tiende a cero, lo que significa que los coeficientes de Fourier convergen a cero más rápido que la potencia k th de n .
tiende a cero, lo que significa que los coeficientes de Fourier convergen a cero más rápido que la potencia k th de n .
Si  pertenece a
pertenece a ![{\ displaystyle L ^ {2} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) , entonces
, entonces  .
.
Si  son coeficientes y
son coeficientes y  entonces hay una función única
entonces hay una función única ![f \ en L ^ 2 ([- \ pi, \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5) tal que
tal que  para cada
para cada  .
.
Teoremas de la convolución [ editar ]
- El primer teorema de convolución establece que si
 y
y  están en
están en ![{\ displaystyle L ^ {1} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21b8374f535846a563ce5f7724edf4023c080b4) , los coeficientes de la serie de Fourier de la convolución periódica 2 π de
, los coeficientes de la serie de Fourier de la convolución periódica 2 π de y
y  estan dados por
estan dados por
-
![[\ widehat {f * _ {2 \ pi} g}] (n) = 2 \ pi \ cdot \ hat {f} (n) \ cdot \ hat {g} (n),](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0) [nb 4]
[nb 4]
- dónde:
-
![{\ displaystyle {\ begin {alineado} \ left [f * _ {2 \ pi} g \ right] (x) \ & \ triangleq \ int _ {- \ pi} ^ {\ pi} f (u) \ cdot g [\ operatorname {pv} (xu)] \, du, && {\ big (} {\ text {and}} \ underbrace {\ operatorname {pv} (x) \ \ triangleq \ operatorname {Arg} (e ^ {ix})} _ {\ text {valor principal}} \, {\ big)} \\ & = \ int _ {- \ pi} ^ {\ pi} f (u) \ cdot g (xu) \, du, && {\ text {when}} g (x) {\ text {is}} 2 \ pi {\ text {-periodic.}} \\ & = \ int _ {2 \ pi} f (u) \ cdot g (xu) \, du, && {\ text {cuando ambas funciones son}} 2 \ pi {\ text {-periódico, y la integral está sobre cualquier}} 2 \ pi {\ text {intervalo.}} \ fin {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2105aae4f5eb50bf6d6541e8a28ef6d0a75db5)
- El segundo teorema de convolución establece que los coeficientes de la serie de Fourier del producto de
 y
y  Están dados por la discreta convolución de la
Están dados por la discreta convolución de la y
y  secuencias:
secuencias:
-
![[\ widehat {f \ cdot g}] (n) = [\ hat {f} * \ hat {g}] (n).](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)
- Una secuencia doblemente infinita.
 en
en  es la secuencia de los coeficientes de Fourier de una función en
es la secuencia de los coeficientes de Fourier de una función en ![{\ displaystyle L ^ {1} ([0,2 \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8) Si y solo si es una convolución de dos secuencias en
Si y solo si es una convolución de dos secuencias en  . Ver [15]
. Ver [15]
Grupos compactos [ editar ]
Una de las propiedades interesantes de la transformada de Fourier que hemos mencionado, es que transporta las convoluciones a productos puntuales. Si esa es la propiedad que buscamos preservar, uno puede producir series de Fourier en cualquier grupo compacto . Los ejemplos típicos incluyen aquellos grupos clásicos que son compactos. Esto generaliza la transformada de Fourier a todos los espacios de la forma L 2 ( G ), donde G es un grupo compacto, de tal manera que la transformada de Fourier lleva las convoluciones a productos puntuales. La serie de Fourier existe y converge de manera similar al caso [- π , π ].
Una extensión alternativa a los grupos compactos es el teorema de Peter-Weyl , que demuestra resultados sobre representaciones de grupos compactos análogos a los de grupos finitos.
Variedades de Riemann [ editar ]
Si el dominio no es un grupo, entonces no hay convolución definida intrínsecamente. Sin embargo, si es un múltiple Riemannian compacto , tiene un operador Laplace-Beltrami . El operador de Laplace-Beltrami es el operador diferencial que corresponde al operador de Laplace para la variedad Riemannian
es un múltiple Riemannian compacto , tiene un operador Laplace-Beltrami . El operador de Laplace-Beltrami es el operador diferencial que corresponde al operador de Laplace para la variedad Riemannian . Entonces, por analogía, uno puede considerar ecuaciones de calor en
. Entonces, por analogía, uno puede considerar ecuaciones de calor en . Dado que Fourier llegó a su base al intentar resolver la ecuación de calor, la generalización natural es utilizar las resoluciones electrónicas del operador Laplace-Beltrami como base. Esto generaliza las series de Fourier a espacios del tipo.
. Dado que Fourier llegó a su base al intentar resolver la ecuación de calor, la generalización natural es utilizar las resoluciones electrónicas del operador Laplace-Beltrami como base. Esto generaliza las series de Fourier a espacios del tipo. , dónde
, dónde  Es una variedad riemanniana. La serie de Fourier converge de manera similar a la
Es una variedad riemanniana. La serie de Fourier converge de manera similar a la![[- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) caso. Un ejemplo típico es tomar
caso. Un ejemplo típico es tomar Ser la esfera con la métrica habitual, en cuyo caso la base de Fourier consiste en armónicos esféricos .
Ser la esfera con la métrica habitual, en cuyo caso la base de Fourier consiste en armónicos esféricos .
Grupos abelianos localmente compactos [ editar ]
La generalización a grupos compactos discutida anteriormente no generaliza a grupos no compactos, no marianos . Sin embargo, existe una generalización directa a los grupos abelianos localmente compactos (LCA).
Esto generaliza la transformada de Fourier a  o
o  , dónde
, dónde  es un grupo de LCA. Si
es un grupo de LCA. Si es compacto, también se obtiene una serie de Fourier, que converge de manera similar a la
es compacto, también se obtiene una serie de Fourier, que converge de manera similar a la ![[- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) caso, pero si
caso, pero si  no es compacta, en su lugar se obtiene una integral de Fourier . Esta generalización produce la transformada de Fourier habitual cuando el grupo Abeliano localmente compacto subyacente es
no es compacta, en su lugar se obtiene una integral de Fourier . Esta generalización produce la transformada de Fourier habitual cuando el grupo Abeliano localmente compacto subyacente es .
.
Tabla de series comunes de Fourier [ editar ]
Algunos pares comunes de funciones periódicas y sus coeficientes de la serie de Fourier se muestran en la tabla a continuación. Se aplica la siguiente notación:
 designa una función periódica definida en
designa una función periódica definida en  .
. designar los coeficientes de la serie de Fourier (forma seno-coseno) de la función periódica
designar los coeficientes de la serie de Fourier (forma seno-coseno) de la función periódica  como se define en Eq.4 .
como se define en Eq.4 .
Dominio del tiempo
 | Trama | Dominio de frecuencia (forma de seno-coseno)
 | Observaciones | Referencia |
|---|
 |
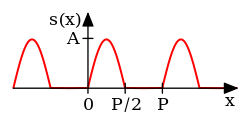
|  | Seno rectificado de onda completa | [16] : p. 193 |
 |
|  | Seno rectificado de media onda | [16] : p. 193 |
 |
|  |  | |
 |
|  | | [16] : p. 192 |
 |
|  | | [16] : p. 192 |
 |
|  | | [16] : p. 193 |
Aproximación y convergencia de series de Fourier [ editar ]
Una cuestión importante tanto para la teoría como para las aplicaciones es la de la convergencia. En particular, a menudo es necesario en aplicaciones para reemplazar la serie infinita. por uno finito,
por uno finito,

Esto se llama una suma parcial . Nos gustaría saber, en qué sentido lo hace. convergen a
convergen a  como
como  .
.
Propiedad de cuadrados mínimos [ editar ]

Tenga en cuenta que  Es un polinomio trigonométrico de grado.
Es un polinomio trigonométrico de grado.  . El teorema de Parseval implica que
. El teorema de Parseval implica que
Teorema. El polinomio trigonométrico. Es el mejor polinomio trigonométrico único del grado.
Es el mejor polinomio trigonométrico único del grado.  aproximando
aproximando  , en el sentido de que, para cualquier polinomio trigonométrico.
, en el sentido de que, para cualquier polinomio trigonométrico.  de grado
de grado  , tenemos
, tenemos

Donde la norma espacial de Hilbert se define como:

Convergencia [ editar ]
Debido a la propiedad de mínimos cuadrados, y debido a la integridad de la base de Fourier, obtenemos un resultado de convergencia elemental.
Teorema. Si pertenece a
pertenece a ![{\ displaystyle L ^ {2} (\ left [- \ pi, \ pi \ right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f) , entonces
, entonces  converge a
converge a  en
en ![{\ displaystyle L ^ {2} (\ left [- \ pi, \ pi \ right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f) , es decir,
, es decir,  converge a 0 como
converge a 0 como  .
.
Ya hemos mencionado que si  es continuamente diferenciable, entonces
es continuamente diferenciable, entonces  Es el n. o coeficiente de Fourier de la derivada.
Es el n. o coeficiente de Fourier de la derivada. . De ello se desprende, esencialmente de la desigualdad de Cauchy-Schwarz , que
. De ello se desprende, esencialmente de la desigualdad de Cauchy-Schwarz , que es absolutamente sumable. La suma de esta serie es una función continua, igual a
es absolutamente sumable. La suma de esta serie es una función continua, igual a , ya que la serie de Fourier converge en la media para
, ya que la serie de Fourier converge en la media para  :
:
Teorema. Si , entonces
, entonces  converge a
converge a  uniformemente (y por lo tanto también puntual ).
uniformemente (y por lo tanto también puntual ).
Este resultado puede ser probado fácilmente si  se supone además que es
se supone además que es  , ya que en ese caso
, ya que en ese caso  tiende a cero como
tiende a cero como  . Más en general, la serie de Fourier es absolutamente sumable, por lo que converge uniformemente a
. Más en general, la serie de Fourier es absolutamente sumable, por lo que converge uniformemente a , siempre que
, siempre que  cumple con una condición de orden de Hölder
cumple con una condición de orden de Hölder . En el caso absolutamente sumable, la desigualdad.
. En el caso absolutamente sumable, la desigualdad. Prueba de convergencia uniforme.
Prueba de convergencia uniforme.
Se conocen muchos otros resultados relacionados con la convergencia de las series de Fourier , que van desde el resultado moderadamente simple que la serie converge en Si
Si  es diferenciable en
es diferenciable en  , al resultado mucho más sofisticado de Lennart Carleson que la serie de Fourier de un
, al resultado mucho más sofisticado de Lennart Carleson que la serie de Fourier de un La función en realidad converge en casi todas partes .
La función en realidad converge en casi todas partes .
Estos teoremas, y las variaciones informales de ellos que no especifican las condiciones de convergencia, a veces se denominan genéricamente "teorema de Fourier" o "teorema de Fourier".









![{\ displaystyle [- \ pi, \ pi] \ times [- \ pi, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\ displaystyle {\ begin {alineado} f (x, y) & = \ sum _ {j, k \, \ in \, \ mathbb {Z} {\ text {(enteros)}}} c_ {j, k } e ^ {ijx} e ^ {iky}, \\ [5pt] c_ {j, k} & = {1 \ sobre 4 \ pi ^ {2}} \ int _ {- \ pi} ^ {\ pi} \ int _ {- \ pi} ^ {\ pi} f (x, y) e ^ {- ijx} e ^ {- iky} \, dx \, dy. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71f5aaa23f00684f16ecbf31838ff5ac61f807db)













![\ begin {align} h ^ \ mathrm {two} (m_1, m_2, x_3) &: = \ frac {1} {a_2} \ int_0 ^ {a_2} h ^ \ mathrm {one} (m_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ frac {m_2} {a_2} x_2} \, dx_2 \\ [12pt] & = \ frac {1} {a_2} \ int_0 ^ {a_2} dx_2 \ frac {1} {a_1} \ int_0 ^ {a_1} dx_1 g (x_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ left (\ frac {m_1} {a_1} x_1 + \ frac {m_2} {a_2} x_2 \ derecha)} \ end {alinear}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)


![\ begin {align} h ^ \ mathrm {three} (m_1, m_2, m_3) &: = frac {1} {a_3} \ int_0 ^ {a_3} h ^ \ mathrm {two} (m_1, m_2, x_3) \ cdot e ^ {- i 2 \ pi \ frac {m_3} {a_3} x_3} \, dx_3 \\ [12pt] & = \ frac {1} {a_3} \ int_0 ^ {a_3} dx_3 \ frac {1} {a_2} \ int_0 ^ {a_2} dx_2 \ frac {1} {a_1} \ int_0 ^ {a_1} dx_1 g (x_1, x_2, x_3) \ cdot e ^ {- i 2 \ pi \ left (\ frac {m_1 } {a_1} x_1 + \ frac {m_2} {a_2} x_2 + \ frac {m_3} {a_3} x_3 \ right)} \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)















![{\ displaystyle {\ begin {vmatrix} {\ dfrac {\ parcial x_ {1}} {\ parcial x}} & {\ dfrac {\ parcial x_ {1}} {\ parcial y}} & {\ dfrac {\ parcial x_ {1}} {\ parcial z}} \\ [12pt] {\ dfrac {\ parcial x_ {2}} {\ parcial x}} & {\ dfrac {\ parcial x_ {2}} {\ parcial y }} & {\ dfrac {\ parcial x_ {2}} {\ parcial z}} \\ [12pt] {\ dfrac {\ parcial x_ {3}} {\ parcial x}} & {\ dfrac {\ parcial x_ {3}} {\ parcial y}} & {\ dfrac {\ parcial x_ {3}} {\ parcial z}} \ fin {vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)










![{\ displaystyle L ^ {2} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)
![[- \ pi, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
















![{\ displaystyle F [n], G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e397cb4324837020cdcdf1d32bb9f00e3bacc3)

![{\ displaystyle a \ cdot F [n] + b \ cdot G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc955a6cf808d4921d875ff75eb9a0ef841fecc9)


![{\ displaystyle F [-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b4a4823263d9c8be71e81b434efa1e0e7f7b78)

![{\ displaystyle F [-n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0bb8e1ac85b41420733bbc3176752128cb2ad1)

![{\ displaystyle F [n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a49c30283e8c78c1a9bedb82bc10d910060b88d)

![{\ displaystyle {\ frac {1} {2}} (F [n] + F [-n] ^ {*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561b550cd40e3a9b9094047184114aa358f1a96b)

![{\ displaystyle {\ frac {1} {2i}} (F [n] -F [-n] ^ {*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2317f4fc3c68ae6247b484faefb4afcfb05dfbb)

![{\ displaystyle \ operatorname {Re} {(F [n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46139e55f1d3fefaedc2c50c143c2070a71cdb80)

![{\ displaystyle \ operatorname {Im} {(F [n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b17cae376b2d16a948caa8532ba478bc7b78dbf)

![{\ displaystyle F [n] \ cdot e ^ {- i {\ frac {2 \ pi x_ {0}} {T}} n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867072969dbc9aa6f27cca71a9ffeb6a6853a75)


![{\ displaystyle F [n-n_ {0}] \!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ff33ce94b62cdac1424cda391a7a63d678bb78)




















![f \ en L ^ 2 ([- \ pi, \ pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)

![{\ displaystyle L ^ {1} ([- \ pi, \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21b8374f535846a563ce5f7724edf4023c080b4)
![[\ widehat {f * _ {2 \ pi} g}] (n) = 2 \ pi \ cdot \ hat {f} (n) \ cdot \ hat {g} (n),](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
![{\ displaystyle {\ begin {alineado} \ left [f * _ {2 \ pi} g \ right] (x) \ & \ triangleq \ int _ {- \ pi} ^ {\ pi} f (u) \ cdot g [\ operatorname {pv} (xu)] \, du, && {\ big (} {\ text {and}} \ underbrace {\ operatorname {pv} (x) \ \ triangleq \ operatorname {Arg} (e ^ {ix})} _ {\ text {valor principal}} \, {\ big)} \\ & = \ int _ {- \ pi} ^ {\ pi} f (u) \ cdot g (xu) \, du, && {\ text {when}} g (x) {\ text {is}} 2 \ pi {\ text {-periodic.}} \\ & = \ int _ {2 \ pi} f (u) \ cdot g (xu) \, du, && {\ text {cuando ambas funciones son}} 2 \ pi {\ text {-periódico, y la integral está sobre cualquier}} 2 \ pi {\ text {intervalo.}} \ fin {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2105aae4f5eb50bf6d6541e8a28ef6d0a75db5)


![[\ widehat {f \ cdot g}] (n) = [\ hat {f} * \ hat {g}] (n).](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)


![{\ displaystyle L ^ {1} ([0,2 \ pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





















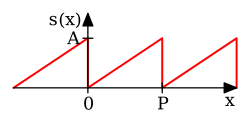


















![{\ displaystyle L ^ {2} (\ left [- \ pi, \ pi \ right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f)









No hay comentarios:
Publicar un comentario