Fourier series ( / f ʊr i eɪ ,

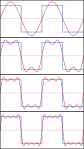
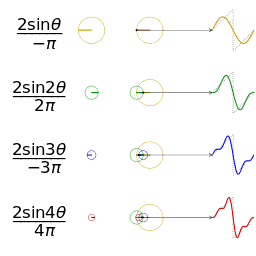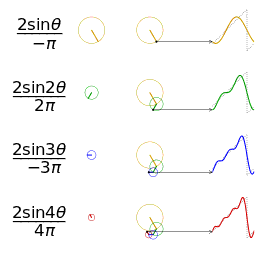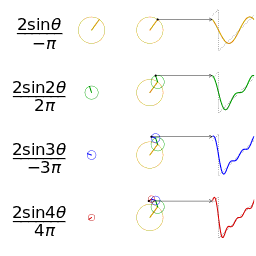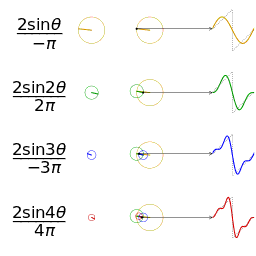
Función (en rojo) es una suma de seis funciones sinusoidales de diferentes amplitudes y frecuencias relacionadas armónicamente. Su resumen se llama una serie de Fourier. La transformada de Fourier,(en azul), que representa la amplitud frente a la frecuencia, revela las 6 frecuencias ( con armónicos impares ) y sus amplitudes ( 1 / número impar ).
Historia[ editar ]
La serie de Fourier se llama así en honor a Jean-Baptiste Joseph Fourier (1768–1830), quien realizó importantes contribuciones al estudio de las series trigonométricas , después de investigaciones preliminares de Leonhard Euler , Jean le Rond d'Alembert y Daniel Bernoulli . [nb 1] Fourier introdujo la serie con el propósito de resolver la ecuación de calor en una placa de metal, publicando sus resultados iniciales en su Métrica sobre la propagación de la piedra en el cuerpo de 1807 ( Tratado sobre la propagación del calor en cuerpos sólidos ) , y publicando su Théorie analytique de la chaleur (Teoría analítica del calor ) en 1822. El Mémoire introdujo el análisis de Fourier, específicamente las series de Fourier. A través de la investigación de Fourier, se estableció el hecho de que una función arbitraria (continua) [2] puede representarse mediante una serie trigonométrica. El primer anuncio de este gran descubrimiento fue hecho por Fourier en 1807, ante la Academia Francesa . [3] Las primeras ideas de descomponer una función periódica en la suma de funciones oscilantes simples se remontan al siglo III a. C., cuando los antiguos astrónomos propusieron un modelo empírico de movimientos planetarios, basado en deferentes y epiciclos .
La ecuación de calor es una ecuación diferencial parcial . Antes del trabajo de Fourier, en el caso general no se conocía ninguna solución a la ecuación del calor, aunque se conocían soluciones particulares si la fuente de calor se comportaba de manera simple, en particular, si la fuente de calor era una onda sinusoidal o coseno . Estas soluciones simples ahora se llaman a veces eigensolutions . La idea de Fourier era modelar una fuente de calor complicada como una superposición (o combinación lineal ) de ondas sinusoidales y coseno simples, y escribir la solución como una superposición de las correspondientes soluciones . Esta superposición o combinación lineal se llama la serie de Fourier.
Desde un punto de vista moderno, los resultados de Fourier son algo informales, debido a la falta de una noción precisa de función e integral a principios del siglo XIX. Más tarde, Peter Gustav Lejeune Dirichlet [4] y Bernhard Riemann [5] [6] [7] expresaron los resultados de Fourier con mayor precisión y formalidad.
Aunque la motivación original era resolver la ecuación de calor, más tarde se hizo evidente que las mismas técnicas podrían aplicarse a una amplia gama de problemas matemáticos y físicos, y especialmente aquellos que involucran ecuaciones diferenciales lineales con coeficientes constantes, para las cuales las soluciones son sinusoides . La serie de Fourier tiene muchas aplicaciones de este tipo en ingeniería eléctrica , análisis de vibraciones , acústica , óptica , procesamiento de señales , procesamiento de imágenes , mecánica cuántica , econometría , [8] teoría de conchas de paredes delgadas , [9] etc.
Definición [ editar ]
Considere una función de valor real, que es integrable en un intervalo de longitud Cuál será el periodo de la serie de Fourier. Ejemplos comunes de intervalos de análisis son :
- y
- y
El proceso de análisis determina los pesos, indexados por entero. que es también el número de ciclos de la Armónico en el intervalo de análisis. Por lo tanto, la duración de un ciclo, en las unidades de es Y la frecuencia armónica correspondiente es y son armónicos, y sus amplitudes (pesos) se encuentran por integración en el intervalo de longitud : [10]
Coeficientes de Fourier
( Ec. 1 )
|
- Si es -periódico, entonces cualquier intervalo de esa longitud es suficiente.
- y Se puede reducir a solo : y
- Muchos textos eligen Para simplificar el argumento de las funciones sinusoidales.
El proceso de síntesis (la serie real de Fourier) es :
Serie de Fourier, forma de seno-coseno.
( Eq.2 )
|
En general, entero es teóricamente infinito. Aun así, la serie podría no converger o igualar exactamente aen todos los valores de (como una discontinuidad de un solo punto) en el intervalo de análisis. Para las funciones de "buen comportamiento" típicas de los procesos físicos, se asume habitualmente la igualdad.
Usando una identidad trigonométrica :
y definiciones: los pares seno y coseno pueden expresarse como una sinusoide única con un desplazamiento de fase, análoga a la conversión entre coordenadas ortogonales (cartesianas) y polares :
Series de Fourier, forma de amplitud-fase.
( Ec . 3 )
|
La forma habitual de generalizar a valor complejo. (la siguiente sección) se obtiene usando la fórmula de Euler para dividir la función coseno en exponenciales complejos. Aquí, la conjugación compleja se denota con un asterisco :
Por lo tanto, con definiciones :
el resultado final es :
Series de Fourier, forma exponencial.
( Eq.4 )
|
Funciones de valor complejo [ editar ]
Si Es una función de valor complejo de una variable real. ambos componentes (parte real e imaginaria) son funciones de valor real que se pueden representar mediante una serie de Fourier. Los dos conjuntos de coeficientes y la suma parcial están dados por :
- y
Definiendo rendimientos :
( Eq.5 )
|
Esto es idéntico a Eq.4 excepto y Ya no son conjugados complejos. La formula paratambién se mantiene sin cambios :
Otras notaciones comunes [ editar ]
La notación es inadecuado para discutir los coeficientes de Fourier de varias funciones diferentes. Por lo tanto, se reemplaza habitualmente por una forma modificada de la función (, en este caso), como por ejemplo o , y la notación funcional a menudo reemplaza los subíndices:
En ingeniería, particularmente cuando la variable representa el tiempo, la secuencia de coeficientes se llama una representación de dominio de frecuencia . Los corchetes se usan a menudo para enfatizar que el dominio de esta función es un conjunto discreto de frecuencias.
Otra representación de dominio de frecuencia utilizada comúnmente utiliza los coeficientes de la serie de Fourier para modular un peine de Dirac :
dónde Representa un dominio de frecuencia continuo. Cuando variable tiene unidades de segundos, Tiene unidades de hertz . Los "dientes" del peine están espaciados en múltiplos (es decir, armónicos ) de, que se llama la frecuencia fundamental . Se puede recuperar de esta representación mediante una transformada de Fourier inversa :
La funcion construida por lo tanto, se suele denominar transformada de Fourier , aunque la integral de Fourier de una función periódica no sea convergente en las frecuencias armónicas. [nb 2]
Convergencia [ editar ]
En aplicaciones de ingeniería , generalmente se presume que la serie de Fourier converge en todas partes excepto en discontinuidades, ya que las funciones encontradas en ingeniería tienen un mejor comportamiento que las que los matemáticos pueden proporcionar como contra-ejemplos a esta presunción. En particular, si Es continua y la derivada de (que puede no existir en todas partes) es cuadrado integrable, entonces la serie de Fourier de converge absoluta y uniformemente a . [11] Si una función es cuadrada-integrable en el intervalo, entonces la serie de Fourier converge a la función en casi todos los puntos . La convergencia de las series de Fourier también depende del número finito de máximos y mínimos en una función que se conoce popularmente como una de las condiciones de Dirichlet para las series de Fourier . Ver la serie de convergencia de Fourier . Es posible definir los coeficientes de Fourier para funciones o distribuciones más generales, en tales casos, la convergencia en la norma o la convergencia débil suele ser de interés.




![{\ displaystyle x \ en [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68354ed86bae40d711eba3ef26c4ec740fcc8fc)

![{\ displaystyle x \ en [- \ pi, \ pi],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f68d2390bdd36e72e19b37682380f02214d52b2)





































![{\ displaystyle {\ begin {alineado} c_ {n} & = {\ frac {1} {P}} \ int _ {P} \ operatorname {Re} \ {s (x) \} \ cdot e ^ {- i {\ tfrac {2 \ pi nx} {P}}} \ dx + i \ cdot {\ frac {1} {P}} \ int _ {P} \ operatorname {Im} \ {s (x) \} \ cdot e ^ {- i {\ tfrac {2 \ pi nx} {P}}} \ dx \\ [4pt] & = {\ frac {1} {P}} \ int _ {P} \ left (\ operatorname {Re} \ {s (x) \} + i \ cdot \ operatorname {Im} \ {s (x) \} \ right) \ cdot e ^ {- i {\ tfrac {2 \ pi nx} {P }}} \ dx \ = \ {\ frac {1} {P}} \ int _ {P} s (x) \ cdot e ^ {- i {\ tfrac {2 \ pi nx} {P}}} \ dx. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ab5a1982824b357f94d5fe7410bfb84fef8e6b)


![{\ displaystyle S [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\ displaystyle {\ begin {alineado} s _ {\ infty} (x) & = \ sum _ {n = - \ infty} ^ {\ infty} {\ hat {s}} (n) \ cdot e ^ {i \, 2 \ pi nx / P} \\ [6pt] & = \ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot e ^ {j \, 2 \ pi nx / P} && \ scriptstyle {\ mathsf {common \ engineering \ notation}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a0ce35db68aa1a4984b746f18928b5d8b6eebfc)
![{\ displaystyle S (f) \ \ triangleq \ \ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot \ delta \ left (f - {\ frac {n} {P}} \ Correcto),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)



![{\ displaystyle {\ begin {alineado} {\ mathcal {F}} ^ {- 1} \ {S (f) \} & = \ int _ {- \ infty} ^ {\ infty} \ left (\ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot \ delta \ left (f - {\ frac {n} {P}} \ right) \ right) e ^ {i2 \ pi fx} \ , df, \\ [6pt] & = \ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot \ int _ {- \ infty} ^ {\ infty} \ delta \ left (f - {\ frac {n} {P}} \ derecha) e ^ {i2 \ pi fx} \, df, \\ [6pt] & = \ sum _ {n = - \ infty} ^ {\ infty} S [ n] \ cdot e ^ {i \, 2 \ pi nx / P} \ \ \ triangleq \ s _ {\ infty} (x). \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)

![{\ displaystyle [x_ {0}, x_ {0} + P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
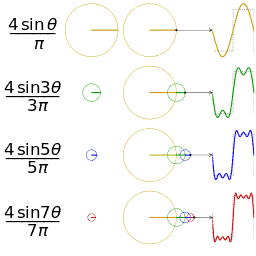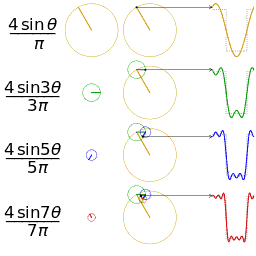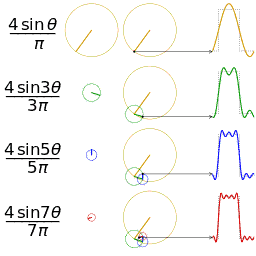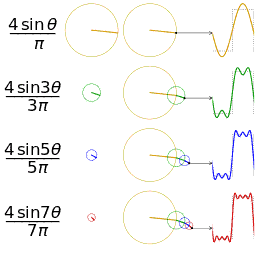

No hay comentarios:
Publicar un comentario