La geometría algebraica es una rama de las matemáticas , que estudia clásicamente ceros de polinomios multivariados . La geometría algebraica moderna se basa en el uso de técnicas algebraicas abstractas, principalmente de álgebra conmutativa , para resolverproblemas geométricos sobre estos conjuntos de ceros.
Los objetos fundamentales de estudio en la geometría algebraica son las variedades algebraicas , que son manifestaciones geométricas de soluciones de sistemas de ecuaciones polinómicas . Ejemplos de las clases más estudiadas de variedades algebraicas son: curvas algebraicas planas , que incluyen líneas , círculos , parábolas , elipses , hiperbolas , curvas cúbicas como curvas elípticas y curvas quárticas como lemniscates y óvalos de Cassini . Un punto del plano pertenece a una curva algebraica si sus coordenadas satisfacen un determinadoecuación polinomial . Las preguntas básicas involucran el estudio de los puntos de especial interés como los puntos singulares , los puntos de inflexión y los puntos en el infinito . Las preguntas más avanzadas involucran la topología de la curva y las relaciones entre las curvas dadas por diferentes ecuaciones.
La geometría algebraica ocupa un lugar central en las matemáticas modernas y tiene múltiples conexiones conceptuales con campos tan diversos como el análisis complejo , la topología y la teoría de los números . Inicialmente, un estudio de sistemas de ecuaciones polinomiales en varias variables, el tema de la geometría algebraica comienza donde la resolución de ecuaciones se detiene , y es aún más importante entender las propiedades intrínsecas de la totalidad de las soluciones de un sistema de ecuaciones, que encontrar un solución específica; esto lleva a algunas de las áreas más profundas de todas las matemáticas, tanto conceptualmente como en términos de técnica.
En el siglo XX, la geometría algebraica se dividió en varias subáreas.
- La corriente principal de la geometría algebraica está dedicada al estudio de los puntos complejos de las variedades algebraicas y, más generalmente, a los puntos con coordenadas en un campo cerrado algebraicamente .
- La geometría algebraica real es el estudio de los puntos reales de una variedad algebraica.
- Geometría Diophantine y, más generalmente, la geometría aritmética es el estudio de los puntos de una variedad algebraica con coordenadas en campos que no son algebraicamente cerrado y se producen en teoría algebraica de números , tales como el campo de los números racionales , campos de número , campos finitos , de función campos , y pcampos -adic .
- Una gran parte de la teoría de la singularidad está dedicada a las singularidades de las variedades algebraicas.
- La geometría algebraica computacional es un área que ha emergido en la intersección de la geometría algebraica y el álgebra computacional , con el auge de las computadoras. Consiste principalmente en el diseño de algoritmos y el desarrollo de software para el estudio de propiedades de variedades algebraicas explícitamente dadas.
Gran parte del desarrollo de la corriente principal de la geometría algebraica en el siglo XX se produjo dentro de un marco algebraico abstracto, con un énfasis creciente en las propiedades "intrínsecas" de las variedades algebraicas que no dependen de ninguna forma particular de integrar la variedad en un espacio de coordenadas ambientales; Esto es paralelo a los desarrollos en topología , geometría diferencial y compleja . Un logro clave de esta geometría algebraica abstracta es la teoría de esquemas de Grothendieck , que permite utilizar la teoría de la gavilla para estudiar variedades algebraicas de una manera muy similar a su uso en el estudio de variedades diferenciales y analíticas.. Esto se obtiene extendiendo la noción de punto: en la geometría algebraica clásica, se puede identificar un punto de una variedad afín, a través del Nullstellensatz de Hilbert , con un ideal máximo del anillo de coordenadas , mientras que los puntos del esquema afín correspondiente son todos ideales ideales de este anillo. Esto significa que un punto de tal esquema puede ser un punto habitual o una subvariedad. Este enfoque también permite una unificación del lenguaje y las herramientas de la geometría algebraica clásica, principalmente relacionadas con puntos complejos, y de la teoría de los números algebraicos. La prueba de Wilesde la larga conjetura llamada último teorema de Fermat es un ejemplo del poder de este enfoque.
Nociones básicas [ editar ]
Ceros de polinomios simultáneos [ editar ]
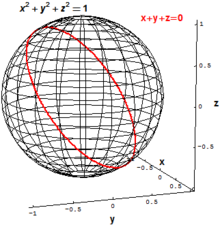
En la geometría algebraica clásica, los principales objetos de interés son los conjuntos de colecciones de polinomios que desaparecen , es decir, el conjunto de todos los puntos que satisfacen simultáneamente una o más ecuaciones polinómicas . Por ejemplo, la esfera bidimensional del radio 1 en el espacio euclidiano tridimensional R 3 podría definirse como el conjunto de todos los puntos ( x , y , z ) con
Un círculo "inclinado" en R 3 se puede definir como el conjunto de todos los puntos ( x , y , z ) que satisfacen las dos ecuaciones polinomiales
Variedades afines [ editar ]
Primero comenzamos con un campo k . En la geometría algebraica clásica, este campo siempre fue los números complejos C , pero muchos de los mismos resultados son verdaderos si asumimos que k está cerrado algebraicamente . Consideramos el espacio afín de la dimensión n sobre k , denotado A n ( k ) (o más simplemente A n , cuando k está claro en el contexto). Cuando se arregla un sistema de coordenadas, se puede identificar A n ( k ) con k n . El propósito de no trabajar conk n es enfatizar que uno "olvida" la estructura del espacio vectorial que k n transporta.
Una función f : A n → A 1 se dice que es polinomial (o regular ) si se puede escribir como un polinomio, es decir, si hay un polinomio p en k [ x 1 , ..., x n ] tal que f ( M ) = p ( t 1 , ..., t n ) para cada punto M con coordenadas ( t 1 , ..., t n ) en A n. La propiedad de una función para ser polinomial (o regular) no depende de la elección de un sistema de coordenadas en A n .
Cuando se elige un sistema de coordenadas, las funciones regulares en el espacio n afín pueden identificarse con el anillo de funciones polinomiales en n variables sobre k . Por lo tanto, el conjunto de las funciones regulares en A n es un anillo, que se denota k [ A n ].
Decimos que un polinomio desaparece en un punto si evaluarlo en ese punto da cero. Sea S un conjunto de polinomios en k [ A n ]. El conjunto de desaparición de S (o locus de desaparición o conjunto de cero ) es el conjunto V ( S ) de todos los puntos en A n donde desaparece todo polinomio en S. Simbólicamente,
Un subconjunto de A n que es V ( S ), para algunos S , se llama un conjunto algebraico . La V significa variedad(un tipo específico de conjunto algebraico que se definirá a continuación).
Dado un subconjunto U de A n , ¿se puede recuperar el conjunto de polinomios que lo generan? Si U es cualquier subconjunto de A n , definir I ( U ) para el conjunto de todos los polinomios cuyo conjunto de fuga contiene U . La I es sinónimo de ideales : si dos polinomios f y g ambos desaparecen en U , entonces f + g anula en U , y si h es cualquier polinomio, entonces hf anula en U, entonces I ( U ) es siempre un ideal del anillo polinomial k [ A n ].
Dos preguntas naturales para hacer son:
- Dado un subconjunto U de A n , ¿cuándo es U = V ( I ( U ))?
- Dado un conjunto S de polinomios, ¿cuándo S = I ( V ( S ))?
La respuesta a la primera pregunta se proporciona al presentar la topología de Zariski , una topología en A ncuyos conjuntos cerrados son los conjuntos algebraicos, y que refleja directamente la estructura algebraica de k [ A n ]. Entonces U = V ( I ( U )) si y solo si U es un conjunto algebraico o, de manera equivalente, un conjunto cerrado de Zariski. La respuesta a la segunda pregunta la da Hilbert's Nullstellensatz . En una de sus formas, dice que I ( V ( S )) es el radical del ideal generado porS . En un lenguaje más abstracto, hay una conexión de Galois , que da lugar a dos operadores de cierre ; se pueden identificar, y naturalmente juegan un papel básico en la teoría; El ejemplo se elabora en la conexión de Galois.
Por diversas razones que no siempre querer trabajar con toda el ideal que corresponde a un conjunto algebraico T . El teorema de base de Hilbert implica que los ideales en k [ A n ] siempre se generan de manera finita.
Un conjunto algebraico se llama irreducible si no se puede escribir como la unión de dos conjuntos algebraicos más pequeños. Cualquier conjunto algebraico es una unión finita de conjuntos algebraicos irreductibles y esta descomposición es única. Por lo tanto, sus elementos se denominan componentes irreductibles del conjunto algebraico. Un conjunto algebraico irreducible también se llama variedad . Resulta que un conjunto algebraico es una variedad si y solo si puede definirse como el conjunto que desaparece de un ideal primordial del anillo polinomial.
Algunos autores no hacen una distinción clara entre conjuntos y variedades algebraicas y usan una variedad irreducible para hacer la distinción cuando sea necesario.
Funciones regulares [ editar ]
Así como las funciones continuas son los mapas naturales en los espacios topológicos y las funciones suavesson los mapas naturales en variedades diferenciables , existe una clase natural de funciones en un conjunto algebraico, llamadas funciones regulares o funciones polinómicas . Una función regular en un conjunto algebraico V contenido en A n es la restricción a V de una función regular en A n . Para un conjunto algebraico definido en el campo de los números complejos, las funciones regulares son uniformes e incluso analíticas .
Puede parecer antinaturalmente restrictivo exigir que una función regular siempre se extienda al espacio ambiental, pero es muy similar a la situación en un espacio topológico normal , donde el teorema de extensión de Tietze garantiza que una función continua en un subconjunto cerrado siempre se extiende al Espacio topológico ambiental.
Al igual que con las funciones regulares en el espacio afín, las funciones regulares en V forman un anillo, que se denota con k [ V ]. Este anillo se denomina anillo de coordenadas de V .
Como las funciones regulares en V provienen de las funciones regulares en A n , existe una relación entre los anillos de coordenadas. Específicamente, si una función regular en V es la restricción de dos funciones f y g en k[ A n ], entonces f - g es una función polinomial que es nula en V y por lo tanto pertenece a I ( V ). Por lo tanto, k[ V ] puede identificarse con k [ A n ] / I ( V ).
Morfismo de variedades afines [ editar ]
Usando funciones regulares de una variedad afín a A 1 , podemos definir mapas regulares de una variedad afín a otra. Primero, definiremos un mapa regular de una variedad al espacio afín: sea V una variedad contenida en A n. Elija m funciones regulares en V , y llámelas f 1 , ..., f m . Definimos un mapa regular f de V a A m dejando f = ( f 1 , ..., f m ). En otras palabras, cada f i determina una coordenada del rango de f .
Si V ′ es una variedad contenida en A m , decimos que f es un mapa regular de V a V ′ si el rango de f está contenido en V ′.
La definición de los mapas regulares se aplica también a los conjuntos algebraicos. Los mapas regulares también se denominan morfismos , ya que convierten la colección de todos los conjuntos algebraicos afines en una categoría , donde los objetos son los conjuntos algebraicos afines y los morfismos son los mapas regulares. Las variedades afines son una subcategoría de la categoría de los conjuntos algebraicos.
Dado un mapa regular g de V a V ′ y una función regular f de k [ V ′], entonces f ∘ g ∈ k [ V ] . El mapa f → f ∘ g es un homomorfismo de anillo de k [ V ′] a k [ V ]. A la inversa, cada homomorfismo de anillo de k [ V '] a k [ V ] define un mapa regular de Va V ′. Esto define una equivalencia de categorías entre la categoría de conjuntos algebraicos y la categoría opuesta de las k -algebras reducidas generadas finamente . Esta equivalencia es uno de los puntos de partida de la teoría de esquemas .
Función racional y equivalencia birracional [ editar ]
A diferencia de las secciones anteriores, esta sección se refiere solo a las variedades y no a los conjuntos algebraicos. Por otro lado, las definiciones se extienden naturalmente a las variedades proyectivas (sección siguiente), ya que una variedad afina y su finalización proyectiva tienen el mismo campo de funciones.
Si V es una variedad afín, su anillo de coordenadas es un dominio de integridad y tiene por lo tanto un campo de fracciones que se denota k ( V ) y llamó al campo de las funciones racionales en V o, en breve, el campo de función de V . Sus elementos son las restricciones a V de las funciones racionales sobre el espacio afín que contiene V . El dominio de una función racional f no es V sino el complemento.de la subvariedad (una hipersuperficie) donde el denominador de f desaparece.
Al igual que con los mapas regulares, uno puede definir un mapa racional de una variedad V a una variedad V '. Al igual que con los mapas regulares, los mapas racionales de V a V 'pueden identificarse con los homomorfismos de campo de k ( V ') a k ( V ).
Dos variedades afines son biracionalmente equivalentes si hay dos funciones racionales entre ellas que son inversas entre sí en las regiones donde se definen ambas. De manera equivalente, son equivalentes biracionalmente si sus campos de función son isomorfos.
Una variedad afín es una variedad racional si es biracionalmente equivalente a un espacio afín. Esto significa que la variedad admite una parametrización racional. Por ejemplo, el círculo de ecuación. Es una curva racional, ya que tiene la parametrización.
que también puede verse como un mapa racional desde la línea hasta el círculo.
El problema de la resolución de las singularidades es saber si cada variedad algebraica es biracionalmente equivalente a una variedad cuya finalización proyectiva no es singular (véase también finalización suave ). Fue resuelto de manera afirmativa en la característica 0 por Heisuke Hironaka en 1964 y aún no se ha resuelto en la característica finita.
Variedad proyectiva [ editar ]
Así como las fórmulas para las raíces de los polinomios de segundo, tercer y cuarto grado sugieren extender los números reales al ajuste más algebraico de los números complejos, muchas propiedades de las variedades algebraicas sugieren extender el espacio afín a un espacio proyectivo más geométricamente completo. Mientras que los números complejos se obtienen al sumar el número i , una raíz del polinomio x 2 + 1 , el espacio proyectivo se obtiene al agregar los puntos apropiados "en el infinito", puntos donde las líneas paralelas pueden coincidir.
Para ver cómo puede ocurrir esto, considere la variedad V ( y - x 2 ) . Si lo dibujamos, obtenemos una parábola . Cuando x va al infinito positivo, la pendiente de la línea desde el origen hasta el punto ( x , x 2 ) también va al infinito positivo. Cuando x va al infinito negativo, la pendiente de la misma línea va al infinito negativo.
Compare esto con la variedad V ( y - x 3 ). Esta es una curva cúbica . Cuando x va al infinito positivo, la pendiente de la línea desde el origen hasta el punto ( x , x 3 ) va al infinito positivo como antes. Pero a diferencia de antes, cuando x va al infinito negativo, la pendiente de la misma línea también va al infinito positivo; exactamente lo contrario de la parábola. Entonces, el comportamiento "en el infinito" de V ( y - x 3 ) es diferente del comportamiento "en el infinito" de V ( y - x 2).
La consideración de la terminación proyectiva de las dos curvas, que es su prolongación "en el infinito" en el plano proyectivo , nos permite cuantificar esta diferencia: el punto en el infinito de la parábola es un punto regular, cuya tangente es la línea en el infinito , mientras que el punto en el infinito de la curva cúbica es una cúspide . Además, ambas curvas son racionales, ya que están parametrizadas por x , y el teorema de Riemann-Rochimplica que la curva cúbica debe tener una singularidad, que debe estar en el infinito, ya que todos sus puntos en el espacio afín son regulares.
Así, muchas de las propiedades de las variedades algebraicas, incluida la equivalencia birracional y todas las propiedades topológicas, dependen del comportamiento "en el infinito" y, por lo tanto, es natural estudiar las variedades en el espacio proyectivo. Además, la introducción de técnicas proyectivas hizo que muchos teoremas en la geometría algebraica sean más simples y agudos: por ejemplo, el teorema de Bézout sobre el número de puntos de intersección entre dos variedades se puede expresar en su forma más aguda solo en el espacio proyectivo. Por estas razones, el espacio proyectivo juega un papel fundamental en la geometría algebraica.
Hoy en día, el espacio proyectivo P n de la dimensión n se define generalmente como el conjunto de líneas que pasan por un punto, considerado como el origen, en el espacio afín de la dimensión n + 1 , o de manera equivalente al conjunto de las líneas vectoriales en una Espacio vectorial de dimensión n + 1 . Cuando se ha elegido un sistema de coordenadas en el espacio de dimensión n + 1 , todos los puntos de una línea tienen el mismo conjunto de coordenadas, hasta la multiplicación por un elemento de k . Esto define las coordenadas homogéneas de un punto de P n como una secuencia de n + 1elementos del campo base k , definidos hasta la multiplicación por un elemento distinto de cero de k (el mismo para toda la secuencia).
Un polinomio en n + 1 variables desaparece en todos los puntos de una línea que pasa por el origen si y solo si es homogéneo . En este caso, se dice que el polinomio se desvanece en el punto correspondiente de P n . Esto nos permite definir un conjunto algebraico proyectivo en P n como el conjunto V ( f 1 , ..., f k ) , donde un conjunto finito de polinomios homogéneos { f 1 , ..., f k }desaparece Al igual que para los conjuntos algebraicos afines, existe una bijección entre los conjuntos algebraicos proyectivos y los ideales homogéneos reducidos que los definen. Las variedades proyectivas son los conjuntos algebraicos proyectivos cuyo ideal definitorio es primordial. En otras palabras, una variedad proyectiva es un conjunto algebraico proyectivo, cuyo anillo de coordenadas homogéneas es un dominio integral , definiéndose el anillo de coordenadas proyectivas como el cociente del anillo graduado o los polinomios en n + 1 variables por el ideal homogéneo (reducido) definiendo la variedad. Cada conjunto algebraico proyectivo puede descomponerse de forma única en una unión finita de variedades proyectivas.
Las únicas funciones regulares que pueden definirse adecuadamente en una variedad proyectiva son las funciones constantes. Por lo tanto, esta noción no se utiliza en situaciones proyectivas. Por otro lado, el campo de las funciones racionales o campo de función es una noción útil que, de manera similar al caso afín, se define como el conjunto de los cocientes de dos elementos homogéneos del mismo grado en el anillo de coordenadas homogéneas.









No hay comentarios:
Publicar un comentario