La geometría epipolar es la geometría de la visión estéreo . Cuando dos cámaras ven una escena 3D desde dos posiciones distintas, hay una serie de relaciones geométricas entre los puntos 3D y sus proyecciones sobre las imágenes 2D que conducen a restricciones entre los puntos de la imagen. Estas relaciones se derivan de la suposición de que las cámaras pueden ser aproximadas por el modelo de cámara de poros .
Geometría epipolar [ editar ]
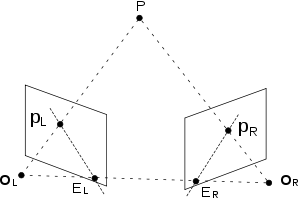
La siguiente figura muestra dos cámaras oscuras que buscan en el punto X . En cámaras reales, el plano de la imagen está realmente detrás del centro focal, y produce una imagen que es simétrica respecto al centro focal de la lente. Aquí, sin embargo, el problema se simplifica colocando un plano de imagen virtual frente al centro focal, es decir, el centro óptico de cada lente de la cámara para producir una imagen que no sea transformada por la simetría. O L y O R representan los centros de simetría de las lentes de las dos cámaras. X representa el punto de interés de ambas cámaras. Puntos x L y x RSon las proyecciones del punto X sobre los planos de la imagen.
Cada cámara captura una imagen 2D del mundo 3D. Esta conversión de 3D a 2D se conoce como una proyección en perspectiva y se describe mediante el modelo de cámara con orificios. Es común modelar esta operación de proyección mediante rayos que emanan de la cámara y pasan por su centro focal. Tenga en cuenta que cada rayo emanante corresponde a un solo punto en la imagen.
Epipolo o punto epipolar [ editar ]
Como los centros ópticos de las lentes de las cámaras son distintos, cada centro se proyecta en un punto distinto en el plano de imagen de la otra cámara. Estos dos puntos de imagen, indicados por e L y e R , se llaman epipolos o puntos epipolares . Ambos epipolos e L y e R en sus respectivos planos de imagen y ambos centros ópticos O L y O R se encuentran en una sola línea 3D.
Línea epipolar [ editar ]
La línea O L - X es vista por la cámara izquierda como un punto porque está directamente en línea con el centro óptico de la lente de esa cámara. Sin embargo, la cámara correcta ve esta línea como una línea en su plano de imagen. Esa línea ( e R - x R ) en la cámara derecha se llama línea epipolar . Simétricamente, la línea O R - Xvista por la cámara derecha como un punto se ve como la línea epipolar e L - x L por la cámara izquierda.
Una línea epipolar es una función de la posición del punto X en el espacio 3D, es decir, a medida que X varía, se genera un conjunto de líneas epipolares en ambas imágenes. Dado que la línea 3D O L - X pasa a través del centro óptico de la lente O L , la línea epipolar correspondiente en la imagen derecha debe pasar a través del epipolo e R (y, en consecuencia, para las líneas epipolares en la imagen izquierda). Todas las líneas epipolares en una imagen contienen el punto epipolar de esa imagen. De hecho, cualquier línea que contiene el punto de epipolar es una línea epipolar ya que se puede derivar de un cierto punto 3D X .
Plano epipolar [ editar ]
Como visualización alternativa, considere los puntos X , O L y O R que forman un plano llamado plano epipolar . El plano epipolar intersecta el plano de imagen de cada cámara donde forma las líneas: las líneas epipolares. Todos los planos epipolares y las líneas epipolares se intersecan con el epipolo, independientemente de dónde se encuentre X.
Restricción epipolar y la triangulación [ editar ]
Si se conoce la posición relativa de las dos cámaras, esto conduce a dos observaciones importantes:
- Suponga que el punto de proyección x L es conocido, y la línea epipolar e R - x R es conocida y el punto X se proyecta en la imagen de la derecha, en un punto x R que debe estar en esta línea epipolar particular. Esto significa que para cada punto observado en una imagen, el mismo punto debe observarse en la otra imagen en una línea epipolar conocida. Esto proporciona una restricción epipolar : la proyección de X en el plano de la cámara derecha x R debe estar contenida en la línea epipolar e R - x R. Tenga en cuenta también que todos los puntos X por ejemplo X 1, X 2 , X 3 en la línea O L - X L verificará esa restricción. Esto significa que es posible probar si dos puntos corresponden al mismo punto 3D. Las restricciones epipolares también pueden ser descritas por la matriz esencial o la matriz fundamental entre las dos cámaras.
- Si se conocen los puntos x L y x R, también se conocen sus líneas de proyección. Si los dos puntos de imagen corresponden al mismo punto 3D X las líneas de proyección deben intersectar con precisión en X . Esto significa que X puede calcularse a partir de las coordenadas de los dos puntos de imagen, un proceso llamado triangulación .
Casos simplificados [ editar ]
La geometría epipolar se simplifica si los dos planos de imagen de la cámara coinciden. En este caso, las líneas epipolares también coinciden ( E L - P L = E R - P R ). Además, las líneas epipolares son paralelas a la línea O L - O Rentre los centros de proyección, y en la práctica puede alinearse con los ejes horizontales de las dos imágenes. Esto significa que para cada punto en una imagen, su punto correspondiente en la otra imagen se puede encontrar mirando solo a lo largo de una línea horizontal. Si las cámaras no pueden colocarse de esta manera, las coordenadas de imagen de las cámaras pueden transformarse para emular tener un plano de imagen común. Este proceso se llama rectificación de imagen .
Geometría epipolar del sensor pushbroom [ editar ]
En contraste con la cámara de marco convencional que utiliza un CCD bidimensional, la cámara de empuje adopta una serie de CCD unidimensionales para producir una tira de imagen larga y continua que se denomina "alfombra de imagen". La geometría epipolar de este sensor es bastante diferente de la de las cámaras de proyección de orificios. Primero, la línea epipolar del sensor pushbroom no es recta, sino una curva de tipo hipérbola. En segundo lugar, el par de 'curva' epipolar no existe. [1] . Sin embargo, en algunas condiciones especiales, la geometría epipolar de las imágenes de satélite podría considerarse como un modelo lineal.
Una geometría finita es cualquier sistema geométrico que tiene solo un número finito de puntos . La geometría euclidiana familiar no es finita, porque una línea euclidiana contiene infinitos puntos. Una geometría basada en los gráficos mostrados en la pantalla de una computadora, donde se considera que los píxeles son los puntos, sería una geometría finita. Si bien hay muchos sistemas que podrían llamarse geometrías finitas, la atención se presta principalmente a los espacios proyectivos y afines finitos debido a su regularidad y simplicidad. Otros tipos significativos de geometría finita son Möbius finito o planos inversos yLos planos de Laguerre , que son ejemplos de un tipo general llamados planos Benz , y sus análogos de dimensiones superiores, como las geometrías inversas finitas superiores .
Las geometrías finitas pueden construirse a través de álgebra lineal , comenzando desde espacios vectoriales sobre un campo finito ; Los planosafines y proyectivos así construidos se llaman geometrías de Galois . Las geometrías finitas también se pueden definir puramente axiomáticamente. Las geometrías finitas más comunes son las geometrías de Galois, ya que cualquier espacio proyectivo finito de dimensión tres o mayor es isomorfo a un espacio proyectivo sobre un campo finito (es decir, la proyectivización de un espacio vectorial sobre un campo finito). Sin embargo, la dimensión dos tiene planos afines y proyectivos que no son isomorfos a las geometrías de Galois, es decir, los planos no desarguesianos.. Resultados similares son válidos para otros tipos de geometrías finitas.
Planos finitos [ editar ]
Las siguientes observaciones se aplican solo a los planos finitos . Hay dos tipos principales de geometría de plano finito: afín y proyectivo . En un plano afín , se aplica el sentido normal de las líneas paralelas . En un plano proyectivo , por el contrario, dos líneas se intersecan en un punto único, por lo que no existen líneas paralelas. Tanto la geometría del plano afín finito como la geometría del plano proyectivo finito pueden describirse mediante axiomas bastante simples .
Planos afines finitos [ editar ]
Una geometría de plano afín es un conjunto no vacío X (cuyos elementos se denominan "puntos"), junto con una colección no vacía L de subconjuntos de X (cuyos elementos se denominan "líneas"), de manera que:
- Por cada dos puntos distintos, hay exactamente una línea que contiene ambos puntos.
- El axioma de Playfair : Dada una línea y un punto no en , existe exactamente una línea que contiene tal que
- Existe un conjunto de cuatro puntos, no tres de los cuales pertenecen a la misma línea.
El último axioma garantiza que la geometría no sea trivial (ya sea vacía o demasiado simple para ser de interés, como una sola línea con un número arbitrario de puntos), mientras que los dos primeros especifican la naturaleza de la geometría.
El plano afín más simple contiene solo cuatro puntos; se llama el plano afín de orden 2. (El orden de un plano afín es el número de puntos en cualquier línea, ver más abajo). Dado que no hay tres colineales, cualquier par de puntos determina una línea única, por lo que este plano contiene seis lineas Corresponde a un tetraedro donde los bordes que no se intersecan se consideran "paralelos", o un cuadrado donde no solo los lados opuestos, sino también las diagonales se consideran "paralelos". Más generalmente, un plano afín finito de orden n tiene n 2puntos y n 2 + n líneas; Cada línea contiene n puntos, y cada punto está en n + 1líneas. El plano afín de orden 3 se conoce como la configuración de Hesse .
Planos proyectivos finitos [ editar ]
Una geometría de plano proyectivo es un conjunto no vacío X (cuyos elementos se denominan "puntos"), junto con una colección no vacía L de subconjuntos de X (cuyos elementos se denominan "líneas"), de manera que:
- Por cada dos puntos distintos, hay exactamente una línea que contiene ambos puntos.
- La intersección de dos líneas distintas contiene exactamente un punto.
- Existe un conjunto de cuatro puntos, no tres de los cuales pertenecen a la misma línea.
Un examen de los dos primeros axiomas muestra que son casi idénticos, excepto que los roles de los puntos y las líneas se han intercambiado. Esto sugiere el principio de dualidad para las geometrías de plano proyectivo, lo que significa que cualquier afirmación verdadera válida en todas estas geometrías permanece verdadera si intercambiamos puntos por líneas y líneas por puntos. La geometría más pequeña que satisface los tres axiomas contiene siete puntos. En este más simple de los planos proyectivos, también hay siete líneas; cada punto está en tres líneas, y cada línea contiene tres puntos.
Este plano proyectivo particular a veces se llama el plano de Fano . Si cualquiera de las líneas se retira del avión, junto con los puntos en esa línea, la geometría resultante es el plano afín de orden 2. El plano de Fano se llama el plano proyectivo de orden 2 porque es único (hasta isomorfismo) . En general, el plano proyectivo de orden n tiene n 2 + n + 1 puntos y el mismo número de líneas; Cada línea contiene n + 1 puntos, y cada punto está en n + 1 líneas.
Una permutación de los siete puntos del plano Fano que lleva puntos colineales (puntos en la misma línea) a los puntos colineales se denomina colinción del plano. El grupo de colineación completa es de orden 168 y es isomorfo al grupo PSL (2,7)≈ PSL (3,2), que en este caso especial también es isomorfo al grupo lineal general GL (3,2) PGL ( 3,2) .
Orden de aviones [ editar ]
Un plano finito de orden n es uno de tal manera que cada línea tenga n puntos (para un plano afín), o tal que cada línea tenga n + 1 puntos (para un plano proyectivo). Una pregunta abierta importante en geometría finita es:
- ¿Es el orden de un plano finito siempre un poder primordial?
Esto se conjetura para ser verdad.
Los planos afines y proyectivos de orden n existen siempre que n es una potencia principal (un número primoelevado a un exponente entero positivo ), mediante el uso de planos afines y proyectivos sobre el campo finito con n = p k elementos. También existen planos no derivados de campos finitos, pero todos los ejemplos conocidos tienen un poder primordial.
- Si n es un entero positivo de la forma 4 k + 1 o 4 k + 2 y n no es igual a la suma de dos cuadrados de enteros , entonces n no aparece como el orden de un plano finito.
El entero más pequeño que no es una potencia principal y no está cubierto por el teorema de Bruck-Ryser es 10; 10 tiene la forma 4 k + 2 , pero es igual a la suma de los cuadrados 1 2 + 3 2 . La no existencia de un plano finito de orden 10 se demostró en una prueba asistida por computadora que terminó en 1989; consulte ( Lam 1991 ) para obtener más información.
El siguiente número más pequeño a considerar es 12, para el cual no se ha demostrado ni un resultado positivo ni negativo.
Historia [ editar ]
Se pueden encontrar ejemplos individuales en el trabajo de Thomas Penyngton Kirkman (1847) y el desarrollo sistemático de la geometría proyectiva finita dada por von Staudt (1856).
El primer tratamiento axiomático de la geometría proyectiva finita fue desarrollado por el matemático italiano Gino Fano . En su trabajo [1] en demostrar la independencia del conjunto de axiomas para proyectiva n -espacio que desarrolló, [2] que consideraba un espacio tridimensional finito con 15 puntos, 35 líneas y 15 planos (ver diagrama), en los cuales Cada línea tenía solo tres puntos. [3]
En 1906, Oswald Veblen y WH Bussey describieron la geometría proyectiva utilizando coordenadas homogéneascon entradas del campo de Galois GF ( q ). Cuando se usan n + 1 coordenadas, la geometría finita n-dimensional se denota PG ( n, q ). [4] Surge en geometría sintética y tiene un grupo de transformación asociado .
Espacios finitos de 3 o más dimensiones [ editar ]
Para algunas diferencias importantes entre la geometría del plano finito y la geometría de los espacios finitos de dimensión superior, consulte el espacio proyectivo axiomático . Para una discusión de los espacios finitos de dimensión superior en general, vea, por ejemplo, las obras de JWP Hirschfeld. El estudio de estos espacios de dimensiones superiores ( n ≥ 3 ) tiene muchas aplicaciones importantes en las teorías matemáticas avanzadas.
Definición axiomática [ editar ]
Un espacio proyectivo S se puede definir axiomáticamente como un conjunto P (el conjunto de puntos), junto con un conjunto L de subconjuntos de P (el conjunto de líneas), que satisfacen estos axiomas: [5]
- Cada dos puntos distintos p y q están exactamente en una línea.
- El axioma de Veblen : [6] Si a , b , c , d son puntos distintos y las líneas a través de ab y cd se encuentran, entonces también lo hacen las líneas a través de ac y bd .
- Cualquier línea tiene al menos 3 puntos en ella.
El último axioma elimina los casos reducibles que pueden escribirse como una unión desunida de espacios proyectivos junto con líneas de 2 puntos que unen dos puntos cualesquiera en espacios proyectivos distintos. De manera más abstracta, se puede definir como una estructura de incidencia ( P , L , I ) que consiste en un conjunto P de puntos, un conjunto L de líneas y una relación de incidencia que indica qué puntos se encuentran en qué líneas.
Obtener un espacio proyectivo finito requiere un axioma más:
- El conjunto de puntos P es un conjunto finito.
En cualquier espacio proyectivo finito, cada línea contiene el mismo número de puntos y el orden del espacio se define como uno menos que este número común.
Un subespacio del espacio proyectivo es un subconjunto X , de manera que cualquier línea que contenga dos puntos de X es un subconjunto de X (es decir, está completamente contenido en X ). El espacio completo y el espacio vacío son siempre subespacios.
Se dice que la dimensión geométrica del espacio es n si ese es el número más grande para el cual existe una cadena de subespacios estrictamente ascendente de esta forma:
Algebraica de construcción [ editar ]
Una construcción algebraica estándar de sistemas satisface estos axiomas. Para un anillo de división Dconstruya un espacio vectorial ( n + 1) tridimensional sobre D (la dimensión del espacio vectorial es el número de elementos en una base). Sean P los subespacios unidimensionales (un solo generador) y L los subespacios bidimensionales (dos generadores independientes) (cerrados por adición vectorial) de este espacio vectorial. La incidencia es la contención. Si D es finito, entonces debe ser un campo finito GF ( q ), ya que según el pequeño teorema de WedderburnTodos los anillos de división finita son campos. En este caso, esta construcción produce un espacio proyectivo finito. Además, si la dimensión geométrica de un espacio proyectivo es al menos tres, entonces hay un anillo de división desde el cual el espacio puede construirse de esta manera. En consecuencia, todos los espacios proyectivos finitos de dimensión geométrica, al menos tres, se definen sobre campos finitos. Un espacio proyectivo finito definido sobre tal campo finito tiene q + 1 puntos en una línea, por lo que los dos conceptos de orden coinciden. Tal espacio proyectivo finito se denota por PG ( n , q ) , donde PG representa la geometría proyectiva, n es la dimensión geométrica de la geometría y q es el tamaño (orden) del campo finito utilizado para construir la geometría.
En general, el número de subespacios k- dimensionales de PG ( n , q ) viene dado por el producto: [7]
Clasificación de los espacios proyectivos finitos por dimensión geométrica [ editar ]
- Dimensión 0 (sin líneas): el espacio es un punto único y está tan degenerado que generalmente se ignora.
- Dimensión 1 (exactamente una línea): Todos los puntos se encuentran en la línea única, llamada línea proyectiva .
- Dimensión 2: Hay al menos 2 líneas, y cualquiera de las dos líneas se encuentran. Un espacio proyectivo para n = 2 es un plano proyectivo . Estos son mucho más difíciles de clasificar, ya que no todos son isomorfos con un PG ( d , q ) . Los planos desarguesianos (aquellos que son isomorfos con un PG (2, q ) ) satisfacen el teorema de Desargues y son planos proyectivos sobre campos finitos, pero hay muchos planos no desarguesianos .
- Dimensión al menos 3: Existen dos líneas que no se intersecan. El teorema de Veblen-Young establece en el caso finito que todo espacio proyectivo de dimensión geométrica n ≥ 3 es isomorfo con un PG ( n , q ) , el espacio proyectivo n- dimensional sobre un campo finito GF ( q ).
El más pequeño de tres espacios proyectivos [ editar ]
El espacio proyectivo tridimensional más pequeño está sobre el campo GF (2) y se denota por PG (3,2). Tiene 15 puntos, 35 líneas y 15 planos. Cada plano contiene 7 puntos y 7 líneas. Cada línea contiene 3 puntos. Como geometrías, estos planos son isomorfos al plano de Fano .
Cada punto está contenido en 7 líneas. Cada par de puntos distintos está contenido exactamente en una línea y cada par de planos distintos se interseca en exactamente una línea.
Colegiala problema de Kirkman [ editar ]
PG (3,2) surge como fondo para una solución del problema de las alumnas de Kirkman , que dice: “Quince alumnas caminan cada día en cinco grupos de tres. Organice la caminata de las niñas durante una semana para que en ese momento, cada par de chicas caminen juntas en un grupo solo una vez. "Hay 35 combinaciones diferentes para que las chicas caminen juntas. También hay 7 días de la semana y 3 niñas en cada grupo. Dos de las siete soluciones no isomórficas a este problema pueden expresarse en términos de estructuras en el espacio Fano 3, PG (3,2), conocidas como empaquetamientos . Una propagaciónde un espacio proyectivo es una partición de sus puntos en líneas desunidas, y un empaquetamiento es una partición de las líneas en esparcimientos desunidos. En PG (3,2), una extensión sería una partición de los 15 puntos en 5 líneas desunidas (con 3 puntos en cada línea), lo que corresponde a la disposición de las alumnas en un día en particular. Un empaque de PG (3,2) consta de siete diferenciales y, por lo tanto, corresponde a una semana completa de arreglos.














No hay comentarios:
Publicar un comentario