Una geometría de taxi es una forma de geometría en la que la función de distancia habitual o la métrica de la geometría euclidiana se reemplaza por una nueva métrica en la que la distancia entre dos puntos es la suma de las diferencias absolutas de sus coordenadas cartesianas . La métrica de taxistambién se conoce como distancia rectilínea , L 1 distancia , L 1 distanciaonorma (ver L p espacio ), serpiente distancia , ciudad distancia bloque , la distancia Manhattan o longitud Manhattan , con variaciones correspondientes en el nombre de la geometría. [1] Los últimos nombres aluden al diseño de cuadrícula de la mayoría de las calles en la isla de Manhattan , lo que hace que el camino más corto que un automóvil pueda tomar entre dos intersecciones en el distrito tenga una longitud igual a la distancia de las intersecciones en la geometría del taxi.
La geometría se ha utilizado en el análisis de regresión desde el siglo XVIII, y hoy en día se le conoce como LASSO . La interpretación geométrica se remonta a la geometría no euclidiana del siglo XIX y se debe a Hermann Minkowski .
Definición formal [ editar ]
La distancia del taxi, , entre dos vectores en un espacio vectorial real n- dimensional con un sistema de coordenadas cartesiano fijo , es la suma de las longitudes de las proyecciones del segmento de línea entre los puntos sobre los ejes de coordenadas . Más formalmente,
Propiedades [ editar ]
La distancia del taxi depende de la rotación del sistema de coordenadas, pero no depende de su reflexión sobre un eje de coordenadas o su traslación . La geometría del taxi satisface todos los axiomas de Hilbert (una formalización de la geometría euclidiana ), excepto el axioma del lado del ángulo lateral , ya que dos triángulos con dos lados igualmente "largos" y un ángulo idéntico entre ellos no suelen ser congruentes a menos que los lados mencionados ser paralelo
Círculos [ editar ]
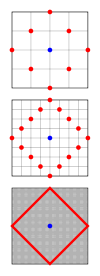
Un círculo es un conjunto de puntos con una distancia fija, llamada radio , desde un punto llamado centro . En la geometría de taxis, la distancia está determinada por una métrica diferente que en la geometría euclidiana, y la forma de los círculos también cambia. Los círculos de los taxis son cuadrados con lados orientados en un ángulo de 45 ° con respecto a los ejes de coordenadas. La imagen de la derecha muestra por qué esto es cierto, mostrando en rojo el conjunto de todos los puntos a una distancia fija de un centro, que se muestra en azul. A medida que disminuye el tamaño de los bloques de la ciudad, los puntos se vuelven más numerosos y se convierten en un cuadrado girado en una geometría de taxis continua. Mientras que cada lado tendría longitudutilizando una métrica euclidiana, donde r es el radio del círculo, su longitud en la geometría del taxi es 2 r . Por lo tanto, la circunferencia de un círculo es 8 r . Así, el valor de un análogo geométrico paraEs 4 en esta geometría. La fórmula para el círculo unitario en taxicab geometry esen coordenadas cartesianas y
Un círculo de radio r para la distancia de Chebyshev ( L ∞ métrica ) en un plano también es un cuadrado con una longitud de lado 2 r paralela a los ejes de coordenadas, por lo que la distancia de Chebyshev planar se puede ver como equivalente por rotación y escala a la distancia de taxi planar. Sin embargo, esta equivalencia entre las métricas L 1 y L ∞ no se generaliza a dimensiones más altas.
Cada vez que cada par en una colección de estos círculos tiene una intersección no vacía, existe un punto de intersección para toda la colección; por lo tanto, la distancia de Manhattan forma un espacio métrico inyectivo .
Aplicaciones [ editar ]
Las medidas de las distancias en el ajedrez [ editar ]
En el ajedrez , la distancia entre los cuadrados en el tablero de ajedrez para torres se mide en la distancia del taxi; los reyes y las reinas usan la distancia de Chebyshev , y los obispos usan la distancia del taxi (entre cuadrados del mismo color) en el tablero de ajedrez girado 45 grados, es decir, con sus diagonales como ejes de coordenadas. Para llegar de una casilla a otra, solo los reyes requieren el número de movimientos igual a su distancia respectiva; torres, reinas y obispos requieren uno o dos movimientos (en un tablero vacío, y suponiendo que el movimiento es posible en todo en el caso del obispo).
Detección comprimida [ editar ]
Al resolver un sistema de ecuaciones lineales no determinado, el término de regularización para el vector de parámetros se expresa en términos de-norma (taxicab geometría) del vector. [2] Este enfoque aparece en el marco de recuperación de señal llamado detección comprimida .
Las diferencias de las distribuciones de frecuencia [ editar ]
La geometría del taxi se puede utilizar para evaluar las diferencias en las distribuciones de frecuencia discretas. Por ejemplo, en el empalme de ARN distribuciones posicionales de hexámeros , que representan la probabilidad de que cada hexámero aparezca en cada nucleótido dadocerca de un sitio de empalme, se puede comparar con la distancia L1. Cada distribución de posición puede representarse como un vector donde cada entrada representa la probabilidad de que el hexámero comience en un determinado nucleótido. Una gran distancia L1 entre los dos vectores indica una diferencia significativa en la naturaleza de las distribuciones, mientras que una distancia pequeña denota distribuciones de forma similar. Esto es equivalente a medir el área entre las dos curvas de distribución porque el área de cada segmento es la diferencia absoluta entre las probabilidades de las dos curvas en ese punto. Cuando se suman para todos los segmentos, proporciona la misma medida que la distancia L1. [3]
Historia [ editar ]
La métrica L 1 se utilizó en el análisis de regresión en 1757 por Roger Joseph Boscovich . [4] La interpretación geométrica data de finales del siglo XIX y el desarrollo de geometrías no euclidianas , en particular por Hermann Minkowski y su desigualdad de Minkowski , de las cuales esta geometría es un caso especial, particularmente usado en la geometría de los números , ( Minkowski 1910 ). La formalización de los espacios L p se acredita a ( Riesz 1910 ).
variedad tórica o incrustación de toro es una variedad algebraica que contiene un toro algebraico como un subconjunto denso abierto , de manera que la acción del toro sobre sí misma se extiende a toda la variedad. Algunos autores también requieren que sea normal . Las variedades tóricas forman una clase importante y rica de ejemplos en geometría algebraica, que a menudo proporcionan un terreno de prueba para los teoremas. La geometría de una variedad tórica está completamente determinada por la combinatoria.de su ventilador asociado, que a menudo hace que los cálculos sean mucho más manejables. Para una cierta clase especial, pero todavía bastante general de variedades tórricas, esta información también se codifica en un politopo, lo que crea una conexión poderosa del sujeto con una geometría convexa. Ejemplos familiares de variedades tóricas son el espacio afín , los espacios proyectivos, los productos de espacios proyectivos y los paquetes sobre el espacio proyectivo .
Variedades toricas de tori [ editar ]
La motivación original para estudiar las variedades tóricas fue estudiar las incrustaciones en el toro. Dado el toro algebraico T , el grupo de caracteres Hom ( T , C x ) forma una red. Dada una colección de puntos A , un subconjunto de esta red, cada punto determina un mapa a C y, por lo tanto, la colección determina un mapa a C | A | . Al tomar el cierre de Zariski de la imagen de dicho mapa, se obtiene una variedad afín. Si la colección de puntos de celosía AGenera el enrejado del personaje, esta variedad es una incrustación de toro. De manera similar, se puede producir una variedad tórica proyectiva parametrizada, tomando el cierre proyectivo del mapa anterior, viéndolo como un mapa en un parche afín de espacio proyectivo.
Dada una variedad tórica proyectiva, observe que podemos probar su geometría por subgrupos de un solo parámetro. Cada uno de los subgrupos de parámetros, determinado por un punto en la red, dual a la red del carácter, es una curva perforada dentro de la variedad tórica proyectiva. Como la variedad es compacta, esta curva perforada tiene un punto límite único. De este modo, al dividir la red del subgrupo de un solo parámetro mediante los puntos límite de las curvas perforadas, obtenemos un ventilador de red, una colección de conos racionales poliédricos. Los conos de dimensión más alta corresponden precisamente a los puntos fijos del toro, los límites de estas curvas perforadas.
La variedad tórica de un fan [ editar ]
Supongamos que N es un grupo abeliano libre de rango finito . Un cono polihédrico racional muy convexo en Nes un cono convexo (del espacio vectorial real de N ) con un vértice en el origen, generado por un número finito de vectores de N , que no contiene una línea a través del origen. Estos serán llamados "conos" para abreviar.
Un ventilador es una colección de conos cerrados bajo intersecciones y caras.
La variedad tórica de un abanico se obtiene tomando las variedades tónicas afines de sus conos y pegándolos entre sí identificando U σ con una subvariedad abierta de U τ siempre que σ sea una cara de τ. Por el contrario, cada abanico de conos racionales fuertemente convexos tiene una variedad tórica asociada.
El abanico asociado con una variedad tórica condensa algunos datos importantes sobre la variedad. Por ejemplo, una variedad es suave si cada cono en su abanico puede ser generado por un subconjunto de una base para el grupo abeliano N libre .
Morfismos de variedades tóricas [ editar ]
Supongamos que Δ 1 y Δ 2 son ventiladores en celosías N 1 y N 2 . Si f es un mapa lineal de N 1 a N 2 de manera que la imagen de cada cono de Δ 1 está contenida en un cono de Δ 2 , entonces f induce un morfismo f * entre las variedades tóricas correspondientes. Este mapa f * es correcto si y solo si el mapa f mapea | Δ 1 | en | Δ 2 |, donde | Δ | es el espacio subyacente de un abanico Δ dado por la unión de sus conos.
Resolución de singularidades [ editar ]
Una variedad tórica es no singular si sus conos de dimensión máxima son generados por una base de la red. Esto implica que cada variedad tórica tiene una resolución de singularidades dada por otra variedad tórica, que se puede construir subdividiendo los conos máximos en conos de variedades tóricas no singulares.
La variedad tórica de un politopo convexo [ editar ]
El abanico de un politopo convexo racional en N consiste en los conos sobre sus caras propias. La variedad tórica del politopo es la variedad tórica de su abanico. Una variación de esta construcción es tomar un politopo racional en el doble de N y tomar la variedad tórica de su conjunto polar en N .
La variedad tórica tiene un mapa del politopo en el dual de N cuyas fibras son toros topológicos. Por ejemplo, el plano proyectivo complejo CP 2 puede representarse por tres coordenadas complejas que satisfacen
donde se ha elegido la suma para dar cuenta de la parte real de reescalado del mapa proyectivo, y las coordenadas deben además identificarse mediante la siguiente acción U (1) :
El enfoque de la geometría tórica es escribir.
Las coordenadas No son negativos, y parametrizan un triángulo porque
es decir,
El triángulo es la base tórica del plano proyectivo complejo. La fibra genérica es un toro dos parametrizado por las fases de; la fase de Puede ser elegido real y positivo por el simetría.
Sin embargo, el toro doble degenera en tres círculos diferentes en el límite del triángulo, es decir, en o o porque la fase de se vuelve intrascendente, respectivamente.
La orientación precisa de los círculos dentro del toro suele representarse por la pendiente de los intervalos de línea (los lados del triángulo, en este caso).
Relación con simetría especular [ editar ]
La idea de variedades tóricas es útil para la simetría de espejo porque una interpretación de ciertos datos de un abanico como datos de un politopo conduce a una construcción geométrica de variedades de espejo.
En matemáticas , la geometría de transformación (o geometría de transformación ) es el nombre de una toma matemática y pedagógicadel estudio de la geometría al centrarse en grupos de transformaciones geométricas y propiedades que son invariantes bajo ellos. Se opone al enfoque clásico de la geometría sintética de la geometría euclidiana , que se centra en demostrar teoremas .
Por ejemplo, dentro de la geometría de transformación, las propiedades de un triángulo isósceles se deducen del hecho de que se asigna a sí mismo mediante una reflexión sobre una determinada línea. Esto contrasta con las pruebas clásicas según los criterios de congruencia de triángulos . [1]
El primer esfuerzo sistemático para utilizar las transformaciones como la base de la geometría fue realizado por Felix Klein en el siglo XIX, bajo el nombre de programa Erlangen . Durante casi un siglo, este enfoque se limitó a los círculos de investigación matemática. En el siglo XX se hicieron esfuerzos para explotarlo para la educación matemática . Andrei Kolmogorov incluyó este enfoque (junto con la teoría de conjuntos ) como parte de una propuesta para la reforma de la enseñanza de la geometría en Rusia . [2] Estos esfuerzos culminaron en la década de 1960 con la reforma general de la enseñanza de las matemáticas conocida como el movimiento New Math .
Pedagogía [ editar ]
Una exploración de la geometría de transformación a menudo comienza con un estudio de la simetría de reflexión que se encuentra en la vida diaria. La primera transformación real es la reflexión en una línea o la reflexión contra un eje . La composición de dos reflexiones da como resultado una rotación cuando las líneas se intersecan, o una traduccióncuando son paralelas. Así, a través de las transformaciones, los estudiantes aprenden sobre la isometría del plano euclidiano.. Por ejemplo, considere la reflexión en una línea vertical y una línea inclinada a 45 ° con respecto a la horizontal. Se puede observar que una composición produce un cuarto de giro en sentido antihorario (90 °) mientras que la composición inversa produce un cuarto de giro en el sentido de las agujas del reloj. Tales resultados muestran que la geometría de transformación incluye procesos no conmutativos .
Una aplicación entretenida de reflexión en una línea se produce en una prueba del triángulo de una séptima área que se encuentra en cualquier triángulo.
Otra transformación introducida a los jóvenes estudiantes es la dilatación . Sin embargo, la reflexión en unatransformación de círculo parece inapropiada para los grados más bajos. Por lo tanto, la geometría inversa , un estudio más amplio que la geometría de transformación de la escuela primaria, suele reservarse para estudiantes universitarios.
Los experimentos con grupos de simetría concretos dan paso a la teoría de grupos abstractos . Otras actividades concretas utilizan cálculos con números complejos , números hipercomplejos o matrices para expresar la geometría de transformación. Estas lecciones de geometría de transformación presentan una vista alternativa que contrasta con la geometría sintética clásica . Cuando los estudiantes se encuentran con la geometría analítica , las ideas de rotaciones de coordenadas y reflexiones se siguen fácilmente. Todos estos conceptos se preparan para el álgebra lineal donde se amplía el concepto de reflexión .
Los educadores han mostrado cierto interés y han descrito proyectos y experiencias con geometría de transformación para niños desde el jardín de infantes hasta la escuela secundaria. En el caso de los niños de muy corta edad, para evitar la introducción de una nueva terminología y establecer vínculos con la experiencia cotidiana de los estudiantes con objetos concretos, a veces se recomendaba usar palabras con las que están familiarizados, como "giros" para reflexiones de líneas ". diapositivas "para las traducciones, y" giros "para las rotaciones, aunque no son un lenguaje matemático preciso. En algunas propuestas, los estudiantes comienzan con objetos concretos antes de realizar las transformaciones abstractas a través de sus definiciones de un mapa de cada punto de la figura. [3] [4] [5] [6]
En un intento por reestructurar los cursos de geometría en Rusia, Kolmogorov sugirió presentarlos bajo el punto de vista de las transformaciones, por lo que los cursos de geometría se estructuraron según la teoría de conjuntos . Esto llevó a la aparición del término "congruente" en las escuelas, para las cifras que antes se llamaban "iguales": como una figura se veía como un conjunto de puntos, solo podía ser igual a sí misma y dos triángulos que podrían superponerse por isometrías se decía que eran congruentes . [2]
Un autor expresó la importancia de la teoría de grupos para la geometría de transformación de la siguiente manera:
- Me he tomado la molestia de desarrollar desde los primeros principios toda la teoría de grupos que necesito, con la intención de que mi libro pueda servir como una primera introducción a los grupos de transformación, y las nociones de teoría de grupos abstracta si nunca las ha visto.































No hay comentarios:
Publicar un comentario