TEMAS DE GEOMETRÍA

La geometría digital trata con conjuntos discretos (generalmente conjuntos de puntos discretos ) que se consideran modelos o imágenes digitalizadas de objetos del espacio euclidiano 2D o 3D .

En pocas palabras, la digitalización es reemplazar un objeto por un conjunto discreto de sus puntos. Las imágenes que vemos en la pantalla del televisor, la visualización de trama de una computadora o en los periódicos son, de hecho, imágenes digitales .

Sus principales áreas de aplicación son gráficos por ordenador y análisis de imágenes .

Los principales aspectos de estudio son:

• Construyendo representaciones digitalizadas de objetos, con énfasis en la precisión y la eficiencia (ya sea por medio de síntesis, ver, por ejemplo, el algoritmo de línea o los discos digitales de Bresenham , o por medio de la digitalización y el procesamiento posterior de las imágenes digitales).
• Estudio de propiedades de conjuntos digitales; Véase, por ejemplo, el teorema de Pick , la convexidad digital , la rectitud digital o la planaridad digital.
• Transformación de representaciones digitalizadas de objetos, por ejemplo (A) en formas simplificadas como (i) esqueletos, mediante la eliminación repetida de puntos simples de manera que la topología digital de una imagen no cambie, o (ii) eje medial, al calcular los máximos locales en una transformación a distancia de la representación de objeto digitalizada dada, o (B) en formas modificadas utilizando morfología matemática .
• Reconstruir objetos "reales" o sus propiedades (área, longitud, curvatura, volumen, área de superficie, etc.) a partir de imágenes digitales.
• Estudio de curvas digitales, superficies digitales y colectores digitales .
• Diseño de algoritmos de seguimiento de objetos digitales.
• Funciones en el espacio digital.

La geometría digital se solapa en gran medida con la geometría discreta y puede considerarse como parte de ella.

Espacio digital [ editar ]

Un espacio digital 2D generalmente significa un espacio de cuadrícula 2D que solo contiene puntos enteros en el espacio euclidiano 2D. Una imagen 2D es una función en un espacio digital 2D (consulte Procesamiento de imágenes ).

En el libro de Rosenfeld y Kak, la conectividad digital se define como la relación entre los elementos en el espacio digital. Por ejemplo, 4-conectividad y 8-conectividad en 2D. También vea la conectividad de píxeles . Un espacio digital y su conectividad (digital) determinan una topología digital .

En el espacio digital, la función digital continua (A. Rosenfeld, 1986) y la función gradualmente variada (L. Chen, 1989) se propusieron de forma independiente.

Una función digital continua significa una función en la que el valor (un número entero) en un punto digital es el mismo o está desactivado a más de 1 de sus vecinos. En otras palabras, si x e y son dos puntos adyacentes en un espacio digital, | f ( x ) -  f ( y ) | ≤ 1.

Una función gradualmente variada es una función de un espacio digital. $${\ displaystyle \ Sigma} a $${\ displaystyle \ {A_ {1}, \ dots, A_ {m} \}} dónde {\ displaystyle A_ {1} <\ cdots  y $${\ displaystyle A_ {i}}son numeros reales Esta función posee la siguiente propiedad: si x e y son dos puntos adyacentes en$${\ displaystyle \ Sigma}asumir $${\ displaystyle f (x) = A_ {i}}, entonces $${\ displaystyle f (y) = A_ {i}}, $${\ displaystyle f (x) = A_ {i + 1}}o $${\ displaystyle A_ {i-1}}. Así que podemos ver que la función gradualmente variada se define como más general que la función digital continua.

A. Rosenfeld (1986) mencionó un teorema de extensión relacionado con las funciones anteriores y lo completó L. Chen (1989). Este teorema establece:$${\ displaystyle D \ subconjunto \ Sigma} y $${\ displaystyle f: D \ rightarrow \ {A_ {1}, \ dots, A_ {m} \}}. La condición necesaria y suficiente para la existencia de la extensión gradualmente variada.$${\ displaystyle F} de $${\ displaystyle f} es: por cada par de puntos $${\ displaystyle x} y $${\ displaystyle y} en $${\ displaystyle D}asumir $${\ displaystyle f (x) = A_ {i}} y $${\ displaystyle f (y) = A_ {j}}, tenemos $${\ displaystyle | ij | \ leq d (x, y)}, dónde $${\ displaystyle d (x, y)} es la distancia (digital) entre $${\ displaystyle x} y $${\ displaystyle y}.

La geometría de la distancia es la caracterización y el estudio de conjuntos de puntos basados únicamente en valores dados de las distancias entre pares de miembros. ^{[1] [2] [3]} Más abstractamente, es el estudio de los espacios semimétricos y las transformaciones isométricas entre ellos. En esta vista, se puede considerar como un tema dentro de la topología general . ^[4]

Históricamente, el primer resultado en geometría de distancia es la fórmula de Heron en el siglo I dC. La teoría moderna comenzó en el siglo XIX con el trabajo de Arthur Cayley , seguido por desarrollos más extensos en el siglo XX por Karl Menger y otros.

Los problemas de geometría de distancia surgen cuando se necesita inferir la forma de una configuración de puntos a partir de las distancias entre ellos, como en biología , ^[4] red de sensores , ^[5] topografía , navegación , cartografía y física .

Introducción y definiciones [ editar ]

Los conceptos de la geometría de la distancia se explicarán primero describiendo dos problemas particulares.

Problema de la navegación hiperbólica.

Primer problema: navegación hiperbólica [ editar ]

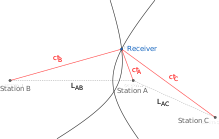
Considere tres estaciones de radio terrestres A, B, C, cuyas ubicaciones son conocidas. Un receptor de radio se encuentra en una ubicación desconocida. Los tiempos que tarda una señal de radio en viajar desde las estaciones al receptor,$${\ displaystyle {\ displaystyle t_ {A}, t_ {B}, t_ {C}}}, son desconocidos, pero las diferencias de tiempo, $${\ displaystyle {\ displaystyle t_ {A} -t_ {B}}} y $${\ displaystyle {\ displaystyle t_ {A} -t_ {C}}}, son conocidos. De ellos, uno sabe las diferencias de distancia.$${\ displaystyle c ({\ displaystyle t_ {A} -t_ {B}})} y $${\ displaystyle c ({\ displaystyle t_ {A} -t_ {C}})}, desde donde se puede encontrar la posición del receptor.

Segundo problema: reducción de dimensión [ editar ]

En el análisis de datos , a menudo a uno se le da una lista de datos representados como vectores$${\ displaystyle \ mathbf {v} = (x_ {1}, \ cdots, x_ {n}) \ in \ mathbb {R} ^ {n}}, y uno necesita descubrir si se encuentran dentro de un subespacio afín de baja dimensión. Una representación de datos de baja dimensión tiene muchas ventajas, como ahorrar espacio de almacenamiento, tiempo de cómputo y brindar una mejor comprensión de los datos.

Definiciones [ editar ]

Ahora formalizamos algunas definiciones que naturalmente surgen al considerar nuestros problemas.

Espacio Semimetric [ editar ]

Dada una lista de puntos en $${\ displaystyle R = \ {P_ {0}, \ cdots, P_ {n} \}}, $${\ displaystyle n \ geq 0}, podemos especificar arbitrariamente las distancias entre pares de puntos por una lista de {\ displaystyle d_ {ij}> 0}, {\ displaystyle 0 \ leq i . Esto define un espacio semimétrico : un espacio métrico sin desigualdad de triángulo .

Explícitamente, definimos un espacio semimétrico como un conjunto no vacío $${\ displaystyle R} Equipado con un semimétrico. $${\ displaystyle d: R \ times R \ a [0, \ infty)} tal que, para todos $${\ displaystyle x, y \ en R},

1. Positividad $${\ displaystyle d (x, y) = 0}   si y solo si  $${\ displaystyle x = y}.
2. Simetría: $${\ displaystyle d (x, y) = d (y, x)}.

Cualquier espacio métrico es a fortiriori un espacio semimétrico. En particular,$${\ displaystyle \ mathbb {R} ^ {k}}, la $${\ displaystyle k}El espacio euclidianotridimensional , es el espacio métrico canónico en geometría de distancia.

La desigualdad del triángulo se omite en la definición, porque no queremos imponer más restricciones en las distancias $${\ displaystyle d_ {ij}} que el mero requisito de que sean positivos.

En la práctica, los espacios semimétricos surgen naturalmente de mediciones inexactas. Por ejemplo, dados tres puntos.$${\ displaystyle A, B, C} en una linea, con $${\ displaystyle d_ {AB} = 1, d_ {BC} = 1, d_ {AC} = 2}, una medida inexacta podría dar $${\ displaystyle d_ {AB} = 0.99, d_ {BC} = 0.98, d_ {AC} = 2.00}, violando la desigualdad del triángulo.

Incrustación isométrica [ editar ]

Dados dos espacios semimétricos, $${\ displaystyle (R, d), (R ', d')}, una inserción isométrica de$${\ displaystyle R} a $${\ displaystyle R '} es un mapa $${\ displaystyle f: R \ to R '} Eso preserva lo semimétrico, es decir, para todos. $${\ displaystyle x, y \ en R}, $${\ displaystyle d (x, y) = d '(f (x), f (y))}.

Por ejemplo, dado el espacio semimétrico finito. $${\ displaystyle (R, d)} definido anteriormente, una incrustación isométrica en se define por puntos $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ en {\ displaystyle \ mathbb {R} ^ {k}}}, tal que $${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}} para todos {\ displaystyle 0 \ leq i .

Independencia afín [ editar ]

Dados los puntos $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ en {\ displaystyle \ mathbb {R} ^ {k}}}, se definen para ser totalmente independientes , si no pueden caber dentro de una sola$${\ displaystyle l}subespacio afín tridimensional de $${\ displaystyle \ mathbb {R} ^ {k}}, para cualquier {\ displaystyle l , si el $${\ displaystyle n}- simplex que abarcan,$${\ displaystyle v_ {n}}tiene positivo $${\ displaystyle n}-volumen, es decir, {\ displaystyle Vol_ {n} (v_ {n})> 0}.

En general, cuando $${\ displaystyle k \ geq n}, son completamente independientes, ya que un n-simplex genérico no es generado. Por ejemplo, 3 puntos en el plano, en general, no son colineales, porque el triángulo que abarcan no degeneran en un segmento de línea. Del mismo modo, 4 puntos en el espacio, en general, no son coplanares, porque el tetraedro que abarcan no degeneran en un triángulo plano.

Cuando {\ displaystyle n> k}, deben ser afinamente dependientes. Esto se puede ver al señalar que cualquier$${\ displaystyle n}-simplex que puede caber dentro $${\ displaystyle \ mathbb {R} ^ {k}} debe ser "plano".

Determinantes de Cayley-Menger [ editar ]

Los determinantes de Cayley-Menger , llamados así por Arthur Cayley y Karl Menger, son determinantes de matrices de distancias entre conjuntos de puntos.

Dejar $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}ser n  + 1 puntos en un espacio semimétrico, su determinante de Cayley-Menger se define por

{\ displaystyle CM (A_ {0}, \ cdots, A_ {n}) = {\ begin {vmatrix} 0 & d_ {01} ^ {2} & d_ {02} ^ {2} & \ cdots & d_ {0n} ^ { 2} & 1 \\ d_ {01} ^ {2} & 0 & d_ {12} ^ {2} & \ cdots & d_ {1n} ^ {2} & 1 \\ d_ {02} ^ {2} & d_ {12} ^ {2 } & 0 & \ cdots & d_ {2n} ^ {2} & 1 \\\ vdots & \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ d_ {0n} ^ {2} & d_ {1n} ^ {2} & d_ {2n} ^ {2} & \ cdots & 0 & 1 \\ 1 & 1 & 1 & \ cdots & 1 & 0 \ end {vmatrix}}}

Si $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ en {\ displaystyle \ mathbb {R} ^ {k}}}, luego forman los vértices de un n-simplex (posiblemente degenerado )$${\ displaystyle {\ displaystyle v_ {n}}} en $${\ displaystyle \ mathbb {R} ^ {k}}.Puede mostrarse que ^[6] el volumen n-dimensional del simplex$${\ displaystyle {\ displaystyle v_ {n}}} satisface

$${\ displaystyle Vol_ {n} (v_ {n}) ^ {2} = {\ frac {(-1) ^ {n + 1}} {(n!) ^ {2} 2 ^ {n}}} CM (A_ {0}, \ cdots, A_ {n})}.

Tenga en cuenta que, para el caso de $${\ displaystyle n = 0}, tenemos $${\ displaystyle Vol_ {0} (v_ {0}) = 1}, lo que significa que el "volumen 0-dimensional" de un 0-simplex es 1, es decir, hay 1 punto en un 0-simplex.

$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}} son afinamente independientes si {\ displaystyle Vol_ {n} (v_ {n})> 0}, es decir, {\ displaystyle (-1) ^ {n + 1} CM (A_ {0}, \ cdots, A_ {n})> 0}. Por lo tanto, los determinantes de Cayley-Menger brindan una manera computacional de probar la independencia afín.

Si {\ displaystyle k , entonces los puntos deben ser afínamente dependientes, por lo tanto $${\ displaystyle CM (A_ {0}, \ cdots, A_ {n}) = 0}. El trabajo de Cayley en 1841 estudió el caso especial de$${\ displaystyle k = 3, n = 4}, es decir, cualquier 5 puntos $${\ displaystyle A_ {0}, \ cdots, A_ {5}} en el espacio tridimensional debe tener $${\ displaystyle CM (A_ {0}, \ cdots, A_ {4}) = 0}.

Historia [ editar ]

El primer resultado en geometría de distancia es la fórmula de Heron , desde el siglo I d. C., que da el área de un triángulo desde las distancias entre sus 3 vértices. La fórmula de Brahmagupta , a partir del siglo VII dC, la generaliza a cuadriláteros cíclicos . Tartaglia , a partir del siglo XVI dC, la generalizó para dar el volumen de tetraedro desde las distancias entre sus 4 vértices.

La teoría moderna de la geometría a distancia comenzó con Authur Cayley y Karl Menger . ^[7] Cayley publicó el determinante de Cayley en 1841 ^[8] , que es un caso especial del determinante general de Cayley-Menger. Menger demostró en 1928 un teorema de caracterización de todos los espacios semimétricos que se pueden incrustar isométricamente en el espacio euclidiano n - dimensional. $${\ displaystyle \ mathbb {R} ^ {n}}. ^[9] [10] En 1931, Menger usó relaciones de distancia para dar un tratamiento axiomático de la geometría euclidiana. ^[11]

Leonard blumenthalEl libro de ^[12] ofrece una descripción general de la geometría de la distancia en el nivel de posgrado, una gran parte de la cual se trata en inglés por primera vez cuando se publicó.

Teorema de caracterización de Menger [ editar ]

Menger demostró el siguiente teorema de caracterización. de de los espacios semimétricos: ^[2]

Un espacio semimétrico. $${\ displaystyle (R, d)} Se puede incrustar isométricamente en el $${\ displaystyle n}espacio euclidiano tridimensional $${\ displaystyle \ mathbb {R} ^ {n}}, pero no en $${\ displaystyle \ mathbb {R} ^ {m}} para cualquier {\ displaystyle 0 \ leq m , si y solo si:

1. $${\ displaystyle R} contiene una $${\ displaystyle (n + 1)}-conjunto de puntos $${\ displaystyle S} Eso es isométrico con una afinidad independiente. $${\ displaystyle (n + 1)}-conjunto de subconjunto de $${\ displaystyle \ mathbb {R} ^ {n}};
2. alguna $${\ displaystyle (n + 3)}-conjunto de puntos $${\ displaystyle S '}, obtenido agregando cualesquiera dos puntos adicionales de $${\ displaystyle R} a $${\ displaystyle S}, es congruente con un $${\ displaystyle (n + 3)}-conjunto de subconjunto de $${\ displaystyle \ mathbb {R} ^ {n}}.

Una prueba de este teorema en una forma ligeramente debilitada (para espacios métricos en lugar de espacios semimétricos) está en ^[13] .

Caracterización a través de los determinantes de Cayley-Menger [ editar ]

Los siguientes resultados se demuestran en el libro de Blumethal ^[12] .

Incrustación $${\ displaystyle n + 1} puntos en $${\ displaystyle \ mathbb {R} ^ {n}}[ editar ]

Dado un espacio semimétrico. $${\ displaystyle (S, d)} , con $${\ displaystyle S = \ {P_ {0}, \ cdots, P_ {n} \}}y $${\ displaystyle d (P_ {i}, P_ {j}) = d_ {ij} \ geq 0}, {\ displaystyle 0 \ leq i , una inserción isométrica de $${\ displaystyle (S, d)} dentro $${\ displaystyle \ mathbb {R} ^ {n}} es definido por $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n} \ en {\ displaystyle \ mathbb {R} ^ {n}}}, tal que $${\ displaystyle d (A_ {i}, A_ {j}) = d_ {ij}} para todos {\ displaystyle 0 \ leq i .

De nuevo, uno pregunta si existe tal incrustación isométrica para $${\ displaystyle (S, d)}.

Una condición necesaria es fácil de ver: para todos. $${\ displaystyle k = 1, \ cdots, n}, dejar $${\ displaystyle v_ {k}}ser el k -simplex formado por $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {k}}, entonces

$${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) = (- 1) ^ {k + 1} CM (A_ {0}, \ cdots, A_ {k}) = 2 ^ {k} (k!) ^ {k} Vol_ {k} (v_ {k}) ^ {2} \ geq 0}

Lo contrario también se sostiene. Es decir, si para todos.$${\ displaystyle k = 1, \ cdots, n},

$${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0},

entonces existe tal incrustación.

Además, tal incrustación es única hasta isometría en $${\ displaystyle \ mathbb {R} ^ {n}}. Es decir, dados dos incrustaciones isométricas definidas por$${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}}y $${\ textstyle A '_ {0}, A' _ {1}, \ ldots, A '_ {n}}, existe una isometría (no necesariamente única) $${\ displaystyle T: \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}, tal que $${\ displaystyle T (A_ {k}) = A '_ {k}} para todos $${\ displaystyle k = 0, \ cdots, n}. Tal$${\ displaystyle T} es único si y solo si $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}) \ neq 0}, es decir, $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n}} son afinamente independientes.

Incrustación $${\ displaystyle n + 2} y $${\ displaystyle n + 3}puntos [ editar ]

Si $${\ displaystyle n + 2} puntos $${\ displaystyle P_ {0}, \ cdots, P_ {n + 1}} se puede incrustar en $${\ displaystyle \ mathbb {R} ^ {n}} como $${\ displaystyle A_ {0}, \ cdots, A_ {n + 1}}, luego de las condiciones anteriores, una condición adicional necesaria es que el $${\ displaystyle (n + 1)}-simplex formado por $${\ textstyle A_ {0}, A_ {1}, \ ldots, A_ {n + 1}}, no debe tener $${\ displaystyle (n + 1)}volumen tridimensional. Es decir,$${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0}.

Lo contrario también se sostiene. Es decir, si para todos.$${\ displaystyle k = 1, \ cdots, n},

$${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0},

y

$${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0},

entonces existe tal incrustación.

Para incrustar $${\ displaystyle n + 3} puntos en $${\ displaystyle \ mathbb {R} ^ {n}}, las condiciones necesarias y suficientes son similares:

1. Para todos $${\ displaystyle k = 1, \ cdots, n}, $${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0};
2. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0};
3. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0};
4. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}.

Incrustar arbitrariamente muchos puntos [ editar ]

los $${\ displaystyle n + 3} El caso resulta suficiente en general.

En general, dado un espacio semimétrico. $${\ displaystyle (R, d)}, se puede incrustar isométricamente en $${\ displaystyle \ mathbb {R} ^ {n}} si y solo si existe $${\ displaystyle P_ {0}, \ cdots, P_ {n} \ en R}, tal que, para todos $${\ displaystyle k = 1, \ cdots, n}, $${\ displaystyle (-1) ^ {k + 1} CM (P_ {0}, \ cdots, P_ {k}) \ geq 0}, y para cualquier $${\ displaystyle P_ {n + 1}, P_ {n + 2} \ en R},

1. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}) = 0};
2. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 2}) = 0};
3. $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}, P_ {n + 1}, P_ {n + 2}) = 0}.

Y tal incrustación es única hasta la isometría en $${\ displaystyle \ mathbb {R} ^ {n}}.

Además, si $${\ displaystyle CM (P_ {0}, \ cdots, P_ {n}) \ neq 0}, entonces no puede ser incrustado isométricamente en ninguna {\ displaystyle \ mathbb {R} ^ {m}, m . Y tal incrustación es única hasta isometría única en$${\ displaystyle \ mathbb {R} ^ {n}}.

Por lo tanto, los determinantes de Cayley-Menger proporcionan una manera concreta de calcular si un espacio semimétrico se puede incrustar en $${\ displaystyle \ mathbb {R} ^ {n}}, para algunos finitos $${\ displaystyle n}, y si es así, ¿cuál es el mínimo? $${\ displaystyle n}.

Aplicaciones [ editar ]

Hay muchas aplicaciones de la geometría de la distancia. ^[3]

En redes de telecomunicaciones como el GPS , se conocen las posiciones de algunos sensores (que se denominan anclas) y también se conocen algunas de las distancias entre los sensores: el problema es identificar las posiciones de todos los sensores. ^[5] Navegación hiperbólica es una tecnología pre-GPS que utiliza la geometría de la distancia para ubicar barcos en función del tiempo que tardan las señales en llegar a las anclas.

Hay muchas aplicaciones en química. ^[4] [12] Técnicas como la RMN pueden medir distancias entre pares de átomos de una molécula dada, y el problema es inferir la forma tridimensional de la molécula desde esas distancias.

Algunos paquetes de software para aplicaciones son:

• DGSOL . Resuelve problemas de geometría de grandes distancias en modelado macromolecular .
• Xplor-NIH . Basado en X-PLOR , para determinar la estructura de las moléculas en base a los datos de los experimentos de RMN. Resuelve problemas de geometría de distancia con métodos heurísticos (como el recocido simulado ) y métodos de búsqueda locales (como la minimización de gradiente de conjugado ).
• TINKER . Modelización y diseño molecular. Puede resolver problemas de geometría a distancia.
• SNLSDPclique . Código MATLAB para ubicar sensores en una red de sensores según las distancias entre los sensores.