TEMAS DE GEOMETRÍA

En geometría , las rotaciones y reflexiones bidimensionales son dos tipos de isometrías planas euclidianas que están relacionadas entre sí.

Una rotación en el plano se puede formar al componer un par de reflexiones. Primero refleje un punto P en su imagen P ′ en el otro lado de la línea L ₁ . Luego refleje P ′ a su imagen P ′ ′ en el otro lado de la línea L ₂ . Si las líneas L ₁ y L ₂ forman un ángulo θ entre sí, los puntos P y P ′ formarán un ángulo 2θ alrededor del punto O , la intersección de L ₁ y L ₂ . Es decir ánguloPOP ′ ′ medirá 2 θ .

Un par de rotaciones sobre el mismo punto O será equivalente a otra rotación alrededor del punto O . Por otro lado, la composición de una reflexión y una rotación, o de una rotación y una reflexión (la composición no es conmutativa ), será equivalente a una reflexión.

Las declaraciones anteriores se pueden expresar más matemáticamente. Deje una rotación alrededor del origen O en un ángulo theta se denota como Rot ( θ ). Deje una reflexión sobre una línea L a través del origen que forma un ángulo θ con el x eje x se denota como Ref ( θ ). Permita que estas rotaciones y reflexiones operen en todos los puntos del plano, y deje que estos puntos se representen mediante vectores de posición . Entonces una rotación puede ser representada como una matriz,

{\ displaystyle \ operatorname {Rot} (\ theta) = {\ begin {bmatrix} \ cos \ theta & - \ sin \ theta \\\ sin \ theta & \ cos \ theta \ end {bmatrix}},}

Y lo mismo para un reflejo.

{\ displaystyle \ operatorname {Ref} (\ theta) = {\ begin {bmatrix} \ cos 2 \ theta & \ sin 2 \ theta \\\ sin 2 \ theta & - \ cos 2 \ theta \ end {bmatrix}} .}

Con estas definiciones de rotación de coordenadas y reflexión, las siguientes cuatro identidades sostienen:

{\ displaystyle {\ begin {alineado} \ operatorname {Rot} (\ theta) \, \ operatorname {Rot} (\ phi) & \ equiv \ operatorname {Rot} (\ theta + \ phi), \\ operatorname { Ref} (\ theta) \, \ operatorname {Ref} (\ phi) & \ equiv \ operatorname {Rot} (2 [\ theta - \ phi]), \\\ operatorname {Rot} (\ theta) \, \ operatorname {Ref} (\ phi) & \ equiv \ operatorname {Ref} \ left (\ phi + {\ frac {1} {2}} \ theta \ right), \\\ operatorname {Ref} (\ phi) \ , \ operatorname {Rot} (\ theta) & \ equiv \ operatorname {Ref} \ left (\ phi - {\ frac {1} {2}} \ theta \ right). \ end {alineado}}}

Estas ecuaciones se pueden probar mediante la multiplicación directa de matrices y la aplicación de identidades trigonométricas .

El conjunto de todas las reflexiones en líneas a través del origen y las rotaciones sobre el origen, junto con la operación de composición de reflexiones y rotaciones, forma un grupo . El grupo tiene una identidad: Rot (0). Cada rotación Rot ( φ ) tiene una Rot inversa (- φ ). Cada reflejo Ref ( θ ) es su propio inverso. La composición tiene cierre y es asociativa, ya que la multiplicación de matrices es asociativa.

Observe que tanto Ref ( θ ) como Rot ( θ ) se han representado con matrices ortogonales . Todas estas matrices tienen un determinante cuyo valor absoluto es la unidad. Las matrices de rotación tienen un determinante de +1, y las matrices de reflexión tienen un determinante de -1.

El conjunto de todas las matrices ortogonales bidimensionales junto con la multiplicación de matrices forman el grupo ortogonal : O (2).

La siguiente tabla da ejemplos de rotación y matriz de reflexión:

Tipo	ángulo θ	matriz
Rotación	0 °	{\ displaystyle {\ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix}}}
Rotación	$${\ displaystyle \ pm}45 °	{\ displaystyle {\ frac {1} {\ sqrt {2}}} {\ begin {pmatrix} 1 & \ mp 1 \\\ pm 1 & 1 \ end {pmatrix}}}
Rotación	90 °	{\ displaystyle {\ begin {pmatrix} 0 & -1 \\ 1 & 0 \ end {pmatrix}}}
Rotación	180 °	{\ displaystyle {\ begin {pmatrix} -1 & 0 \\ 0 & -1 \ end {pmatrix}}}
Reflexión	0 °	{\ displaystyle {\ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix}}}
Reflexión	45 °	{\ displaystyle {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix}}}
Reflexión	90 °	{\ displaystyle {\ begin {pmatrix} -1 & 0 \\ 0 & 1 \ end {pmatrix}}}
Reflexión	-45 °	{\ displaystyle {\ begin {pmatrix} 0 & -1 \\ - 1 & 0 \ end {pmatrix}}}

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Una traducción mueve cada punto de una figura o un espacio en la misma cantidad en una dirección determinada.

Una reflexión en contra de un eje seguida por una reflexión en contra de un segundo eje paralelo al primero da como resultado un movimiento total que es una traslación.

En la geometría euclidiana , una traducción es una transformación geométrica que mueve todos los puntos de una figura o un espacio en la misma distancia en una dirección determinada.

En la geometría euclidiana, una transformación es una correspondencia de uno a uno entre dos conjuntos de puntos o un mapeo de un plano a otro. ^[1] Una traducción se puede describir como un movimiento rígido : los otros movimientos rígidos son rotaciones , reflejos y reflejos de deslizamiento .

Una traducción también puede interpretarse como la adición de un vectorconstante a cada punto, o como un desplazamiento del origen del sistema de coordenadas .

Un operador de traducción es un operador. $${\ displaystyle T _ {\ mathbf {\ delta}}} tal que $${\ displaystyle T _ {\ mathbf {\ delta}} f (\ mathbf {v}) = f (\ mathbf {v} + \ mathbf {\ delta}).}

Si v es un vector fijo, entonces la traducción T _v funcionará como T _v : ( p) = p + v .

Si T es una traducción, a continuación, la imagen de un subconjunto Abajo la función T es el traducen de una por T . El traductor de A por T _{v a}menudo se escribe A + v .

En un espacio euclidiano , cualquier traducción es una isometría . El conjunto de todas las traducciones forma el grupo de traducción T , que es isomorfo al espacio en sí, y un subgrupo normal del grupo euclidiano E ( n ). El grupo cociente de E ( n ) por T es isomorfo al grupo ortogonal O ( n ):

E ( n ) / T ≅ O ( n ).

Representación de la matriz [ editar ]

Una traducción es una transformación afín con no hay puntos fijos . Las multiplicaciones de matrices siempretienen el origen como un punto fijo. Sin embargo, hay una solución común que utiliza coordenadas homogéneaspara representar una traducción de un espacio vectorial con la multiplicación de matrices : escriba el vector tridimensional w = ( w _x , w _y , w _z ) usando 4 coordenadas homogéneas como w = ( w _x , w _y ,w _z , 1). ^[2]

Para traducir un objeto por un vector v , cada vector homogéneo p (escrito en coordenadas homogéneas) se puede multiplicar por esta matriz de traducción :

{\ displaystyle T _ {\ mathbf {v}} = {\ begin {bmatrix} 1 & 0 & 0 & v_ {x} \\ 0 & 1 & 0 & v_ {y} \\ 0 & 0 & 1 & v_ {z} \\ 0 & 0 & 0 & 1 & 1 \ end {bmatrix}}}

Como se muestra a continuación, la multiplicación dará el resultado esperado:

{\ displaystyle T _ {\ mathbf {v}} \ mathbf {p} = {\ begin {bmatrix} 1 & 0 & 0 & v_ {x} \\ 0 & 1 & 0 & v_ {y} \\ 0 & 0 & 1 & v_ {z} \\ 0 & 0 & 0 & 1 \ end {bmatrix}} { begin {bmatrix} p_ {x} \\ p_ {y} \\ p_ {z} \\ 1 \ end {bmatrix}} = {\ begin {bmatrix} p_ {x} + v_ {x} \\ p_ {y } + v_ {y} \\ p_ {z} + v_ {z} \\ 1 \ end {bmatrix}} = \ mathbf {p} + \ mathbf {v}}

La inversa de una matriz de traducción se puede obtener invirtiendo la dirección del vector:

$${\ displaystyle T _ {\ mathbf {v}} ^ {- 1} = T _ {- \ mathbf {v}}. \!}

De manera similar, el producto de las matrices de traducción se da al agregar los vectores:

$${\ displaystyle T _ {\ mathbf {u}} T _ {\ mathbf {v}} = T _ {\ mathbf {u} + \ mathbf {v}}. \!}

Debido a que la adición de vectores es conmutativa , la multiplicación de matrices de traducción también es conmutativa (a diferencia de la multiplicación de matrices arbitrarias).

Traducciones en física [ editar ]

En física , la traslación (movimiento traslacional) es un movimiento que cambia la posición de un objeto, en oposición a la rotación . Por ejemplo, según Whittaker: ^[3]

Si un cuerpo se mueve de una posición a otra, y si las líneas que unen los puntos inicial y final de cada uno de los puntos del cuerpo son un conjunto de líneas rectas paralelas de longitud ℓ , de modo que la orientación del cuerpo en el espacio sea inalterado, el desplazamiento se denomina traslación paralela a la dirección de las líneas, a través de una distancia ℓ .

-  ET Whittaker : Un tratado sobre la dinámica analítica de partículas y cuerpos rígidos , p. 1

Una traducción es la operación que cambia las posiciones de todos los puntos ( x , y , z ) de un objeto de acuerdo con la fórmula

$${\ displaystyle (x, y, z) \ to (x + \ Delta x, y + \ Delta y, z + \ Delta z)}

dónde $${\ displaystyle (\ Delta x, \ \ Delta y, \ \ Delta z)}Es el mismo vector para cada punto del objeto. El vector de traduccion$${\ displaystyle (\ Delta x, \ \ Delta y, \ \ Delta z)}común a todos los puntos del objeto describe un tipo particular de desplazamiento del objeto, generalmente llamado desplazamiento lineal para distinguirlo de los desplazamientos que involucran rotación, llamados desplazamientos angulares .

Cuando se considera el espacio-tiempo , un cambio de coordenada de tiempo se considera una traducción. Por ejemplo, el grupo de Galileo y el grupo de Poincaré incluyen traducciones con respecto al tiempo.

Este artículo puede ser demasiado técnico para que la mayoría de los lectores lo entiendan . Ayude a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Diciembre de 2016 ) (Aprenda cómo y cuándo eliminar este mensaje de plantilla )

El funcionamiento de una reflexión deslizante: un compuesto de una reflexión a través de una línea y una traducción paralela a la línea de reflexión.

Dado que esta huella de huella tiene simetría de reflexión de deslizamiento, la aplicación de la operación de reflexión de deslizamiento asignará cada huella izquierda en una huella derecha y cada huella derecha en una huella izquierda, lo que llevará a una configuración final que no se puede distinguir del original.

En la geometría bidimensional , una reflexión de planeo (o transflección ) es una operación de simetría que consiste en una reflexión sobre una línea y luego la traducción a lolargo de esa línea, combinada en una sola operación. El paso intermedio entre la reflexión y la traducción puede verse diferente de la configuración inicial, por lo que los objetos con simetría de deslizamiento son, en general, no simétricos solo en la reflexión. En teoría de grupos , el plano de planeo se clasifica como un tipo de isometría opuesta del plano euclidiano

Un único deslizamiento se representa como grupo de frisop11g. Una reflexión de planeo se puede ver como una limitación de rotación , donde la rotación se convierte en una traslación. También se le puede dar una notación de Schoenflies como S _2∞ , notación de Coxeter como [∞ ⁺ , 2 ⁺] y notación de orbifold como ∞ ×.

Descripción [ editar ]

La combinación de una reflexión en una línea y una traducción en una dirección perpendicular es una reflexión en una línea paralela. Sin embargo, un reflejo de deslizamiento no puede ser reducido de esa manera. Por lo tanto, el efecto de una reflexión combinada con cualquier traducción es una reflexión deslizante, con un caso especial solo una reflexión. Estos son los dos tipos de isometrías indirectas en 2D .

Por ejemplo, hay una isometría que consiste en la reflexión sobre el eje x , seguida de la traducción de una unidad paralela a ella. En coordenadas, lleva

( x , y ) → ( x + 1, - y ).

Arregla un sistema de líneas paralelas.

El grupo de isometría generado por solo una reflexión deslizante es un grupo cíclico infinito . ^[1]

La combinación de dos reflexiones de deslizamiento iguales da una traducción pura con un vector de traducción que es el doble de la reflexión de deslizamiento, por lo que los poderes pares de la reflexión de deslizamiento forman un grupo de traducción.

En el caso de la simetría de reflexión de planeo , el grupo de simetría de un objeto contiene una reflexión de planeo y, por lo tanto, el grupo generado por él. Si eso es todo lo que contiene, este tipo es frieze group p11g.

Ejemplo de patrón con este grupo de simetría:

Grupo friso n. 6 (reflexiones de deslizamiento, traslaciones y rotaciones) se genera mediante una reflexión de deslizamiento y una rotación alrededor de un punto en la línea de reflexión. Es isomorfo a un producto semidirecto de Z y C ₂ .

Ejemplo de patrón con este grupo de simetría:

Un ejemplo típico de reflejo de deslizamiento en la vida cotidiana sería la huella de huellas dejadas en la arena por una persona que camina en una playa.

Para cualquier grupo de simetría que contenga alguna simetría de reflexión deslizante, el vector de traducción de cualquier reflexión deslizante es la mitad de un elemento del grupo de traducción. Si el vector de traslación de una reflexión deslizante es en sí mismo un elemento del grupo de traducción, entonces la simetría de reflexión deslizante correspondiente se reduce a una combinación de simetría de reflexión y simetría traslacional .

La simetría de reflexión deslizante con respecto a dos líneas paralelas con la misma traslación implica que también hay simetría traslacional en la dirección perpendicular a estas líneas, con una distancia de traslación que es el doble de la distancia entre las líneas de reflexión deslizante. Esto corresponde al grupo de papel tapiz pg; con simetría adicional ocurre también en pmg, pgg y p4g.

Si también hay líneas de reflexión verdaderas en la misma dirección, entonces están espaciadas uniformemente entre las líneas de reflexión deslizantes. Una línea de reflexión deslizante paralela a una línea de reflexión verdadera ya implica esta situación. Esto corresponde al grupo de papel tapiz cm. La simetría de traslación viene dada por los vectores de traslación oblicuos de un punto en una línea de reflexión verdadera a dos puntos en el siguiente, que soporta un rombo con la línea de reflexión verdadera como una de las diagonales. Con simetría adicional, también ocurre en cmm, p3m1, p31m, p4m y p6m.

En 3D el reflejo de planeo se llama plano de planeo . Es un reflejo en un plano combinado con una traslación paralela al plano.

Grupos de papel tapiz [ editar ]

En el plano euclidiano, 3 de los 17 grupos de papel tapiz requieren generadores de reflexión deslizante. p2gg tiene reflejos de deslizamiento ortogonales y rotaciones de 2 veces. cm tiene espejos y deslizamientos paralelos, y pg tiene deslizamientos paralelos. (Reflexiones de deslizamiento se muestran a continuación como líneas discontinuas)

Dominio de grupo de fondo de pantalla, y dominios fundamentales (amarillo)

Nombre cristalografico	pgg	cm	pg
Nombre de Conway	22 ×	* ×	××
Diagrama
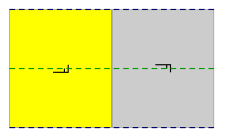
Ejemplo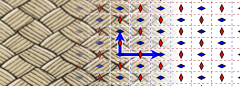

Reflexión de deslizamiento en la naturaleza y juegos [ editar ]

La simetría de deslizamiento se puede observar en la naturaleza entre ciertos fósiles de la biota de Ediacara ; los machaeridian ; y ciertos gusanos palaeoscolecidos . ^[2] También se puede ver en muchos grupos existentes de corrales marinos . ^[3]

La reflexión de planeo es común en el juego de la vida de Conway cuando se produce Gun (autómata celular) .