TEMAS DE GEOMETRÍA

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Tipos de secciones cónicas: 
1. Parábola
2. Círculo y elipse
3. Hipérbola

Tabla de cónicas, Cyclopaedia , 1728.

En matemáticas , una sección cónica (o simplemente cónica ) es una curva obtenida como la intersección de la superficie de un cono con un plano . Los tres tipos de sección cónica son la hipérbola , la parábola y la elipse ; El círculo es un caso especial de la elipse, aunque históricamente a veces se lo llamó un cuarto tipo. Los antiguos matemáticos griegos estudiaron secciones cónicas, que culminaron alrededor del año 200 aC con el trabajo sistemático de Apolonio de Perga sobre sus propiedades.

Las secciones cónicas en el plano euclidiano tienen varias propiedades distintivas, muchas de las cuales se pueden usar como definiciones alternativas. Una de estas propiedades define una cónica no circular ^[1] como el conjunto de aquellos puntos cuyas distancias a algún punto en particular, llamado enfoque , y alguna línea en particular, llamada directriz , están en una proporción fija, llamada la excentricidad . El tipo de cónica está determinado por el valor de la excentricidad. En geometría analítica , una cónica puede definirse como una curva algebraica plana de grado 2; es decir, como el conjunto de puntos cuyas coordenadas satisfacen una ecuación cuadráticaen dos variables Esta ecuación puede escribirse en forma de matriz, y algunas propiedades geométricas pueden estudiarse como condiciones algebraicas.

En el plano euclidiano, los tres tipos de secciones cónicas parecen bastante diferentes, pero comparten muchas propiedades. Al extender el plano euclidiano para incluir una línea en el infinito, obteniendo un plano proyectivo , la diferencia aparente se desvanece: las ramas de una hipérbola se encuentran en dos puntos en el infinito, lo que lo convierte en una sola curva cerrada; y los dos extremos de una parábola se unen para convertirla en una curva cerrada tangente a la línea en el infinito. Una extensión adicional, al expandir las coordenadas reales para admitir coordenadas complejas , proporciona los medios para ver esta unificación algebraicamente.

Geometría euclidiana

Las secciones cónicas se han estudiado durante miles de años y han proporcionado una fuente rica de resultados interesantes y hermosos en geometría euclidiana .

Definición

Los límites negros de las regiones coloreadas son secciones cónicas. No se muestra la otra mitad de la hipérbola, que se encuentra en la otra mitad no mostrada del cono doble.

Una cónica es la curva obtenida como la intersección de un plano , llamada el plano de corte , con la superficie de un cono doble (un cono con dos nappes ). Se debe suponer que el cono es un cono circular recto con el propósito de una descripción fácil, pero esto no es obligatorio; Cualquier doble cono con alguna sección transversal circular será suficiente. Los planos que pasan a través del vértice del cono intersecarán el cono en un punto, una línea o un par de líneas que se intersecan. Estas se llaman cónicas degeneradas y algunos autores no las consideran cónicas en absoluto. A menos que se indique lo contrario, "cónica" en este artículo se referirá a una cónica no degenerada.

Hay tres tipos de cónicas: la elipse , la parábola y la hipérbola . El círculo es un tipo especial de elipse, aunque históricamente Apolonio es considerado como un cuarto tipo. Las elipses surgen cuando la intersección del cono y el plano es una curva cerrada . El círculo se obtiene cuando el plano de corte es paralelo al plano del círculo generador del cono; para un cono derecho, esto significa que el plano de corte es perpendicular al eje. Si el plano de corte es paralelo a exactamente una línea generadora del cono, entonces la cónica es ilimitada y se llama parábola . En el caso restante, la figura es una hipérbola.: el plano cruza las dos mitades del cono, produciendo dos curvas sin límites separadas.

Excentricidad, enfoque y directriz.

Círculo ( e = 0), elipse ( e = 1/2), parábola ( e= 1) e hipérbola ( e = 2) con enfoque fijo F y directriz ( e =).

Alternativamente, uno puede definir una sección cónica puramente en términos de geometría plana: es el lugar de todos los puntos P cuya distancia a un punto fijo F (llamado enfoque ) es un múltiplo constante (llamado la excentricidad e) de la distancia desde P a una línea fija L (llamada directriz ). Para 0 < e <1 font=""> obtenemos una elipse, para e = 1 una parábola, y para e > 1 una hipérbola.

Un círculo es un caso limitante y no está definido por un enfoque y una directriz en el plano euclidiano. La excentricidad de un círculo se define como cero y su enfoque es el centro del círculo, pero su directriz solo puede tomarse como la línea en el infinito en el plano proyectivo. ^[2]

La excentricidad de una elipse se puede ver como una medida de lo lejos que se desvía la elipse de ser circular.

Si el ángulo entre la superficie del cono y su eje es $${\ displaystyle \ beta} y el ángulo entre el plano de corte y el eje es $${\ displaystyle \ alpha,}la excentricidad es ^[3] $${\ displaystyle {\ frac {\ cos \ alpha} {\ cos \ beta}}.}

El uso de las esferas de Dandelin facilita una prueba de que las curvas anteriores definidas por la propiedad directriz de enfoque son las mismas que las obtenidas por los planos que intersectan un cono . ^[4]

Parámetros cónicos

Parámetros cónicos en el caso de una elipse.

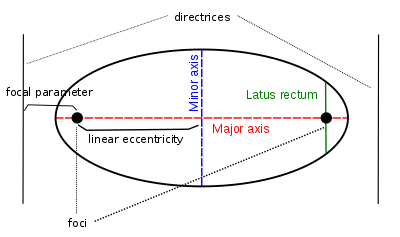
Además de la excentricidad ( e ), los focos y la directriz, varias características geométricas y longitudes están asociadas con una sección cónica.

El eje principal es la línea que une los focos de una elipse o hipérbola, y su punto medio es el centro de la curva . Una parábola no tiene centro.

La excentricidad lineal ( c ) es la distancia entre el centro y un foco.

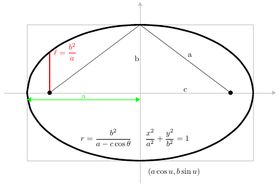
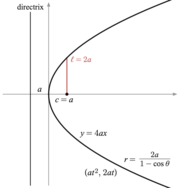
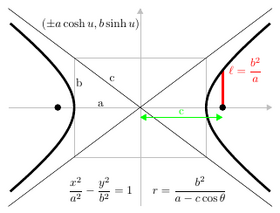
El latus recto es la cuerda paralela a la directriz y pasa a través de un foco; su longitud media es el recto semi-latus ( ℓ ).

El parámetro focal ( p ) es la distancia desde un foco a la directriz correspondiente.

El eje mayor es el acorde entre los dos vértices: el acorde más largo de una elipse, el acorde más corto entre las ramas de una hipérbola. Su longitud media es el eje semi-mayor ( a ). Cuando una elipse o hipérbola están en posición estándar como en las ecuaciones a continuación, con el foco en el eje x y el centro en el origen, los vértices de la cónica tienen coordenadas (- a , 0) y ( a , 0) , con una no negativo

El eje menor es el acorde más corto de una elipse, y su longitud media es el eje semi menor ( b ), el mismo valor b que en la siguiente ecuación estándar. Por analogía, para una hipérbola también llamamos al parámetro b en la ecuación estándar el eje semi-menor.

Las siguientes relaciones son válidas: ^[5]

• $${\ displaystyle \ \ ell = pe}
• $${\ displaystyle \ c = ae}
• $${\ displaystyle \ p + c = {\ frac {a} {e}}}

Para las cónicas en posición estándar, estos parámetros tienen los siguientes valores, tomando {\ displaystyle a, b> 0}.

sección cónica	ecuación	excentricidad ( e )	excentricidad lineal ( c )	semi-latus recto ( ℓ )	parámetro focal ( p )
circulo	$${\ displaystyle x ^ {2} + y ^ {2} = a ^ {2} \,}	$${\ displaystyle 0 \,}	$${\ displaystyle 0 \,}	$${\ displaystyle a \,}	$${\ displaystyle \ infty}
elipse	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1}	$${\ displaystyle {\ sqrt {1 - {\ frac {b ^ {2}} {a ^ {2}}}}}	$${\ displaystyle {\ sqrt {a ^ {2} -b ^ {2}}}}	$${\ displaystyle {\ frac {b ^ {2}} {a}}}	$${\ displaystyle {\ frac {b ^ {2}} {\ sqrt {a ^ {2} -b ^ {2}}}}}
parábola	$${\ displaystyle y ^ {2} = 4ax \,}	$${\ displaystyle 1 \,}	N / A	$${\ displaystyle 2a \,}	$${\ displaystyle 2a \,}
hipérbola	$${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1}	$${\ displaystyle {\ sqrt {1 + {\ frac {b ^ {2}} {a ^ {2}}}}}	$${\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}}}	$${\ displaystyle {\ frac {b ^ {2}} {a}}}	$${\ displaystyle {\ frac {b ^ {2}} {\ sqrt {a ^ {2} + b ^ {2}}}}}

Formas standard en coordenadas cartesianas.

Formas estándar de una elipse.

Formas estándar de una parábola.

Formas estándar de una hipérbola.

Después de introducir las coordenadas cartesianas , la propiedad focus-directrix se puede usar para producir las ecuaciones que satisfacen los puntos de la sección cónica. ^[6] Por medio de un cambio de coordenadas ( rotación y traslación de ejes ) estas ecuaciones se pueden poner en formas estándar . ^[7] Para las elipses e hipérbolas, una forma estándar tiene el eje xcomo eje principal y el origen (0,0) como centro. Los vértices son (± a , 0) y los focos (± c , 0) . Define b mediante las ecuaciones c ² = a ²- b ² para una elipse y c ² = a ² + b ² para una hipérbola. Para un círculo, c = 0 entonces a ² = b ² . Para la parábola, la forma estándar tiene el enfoque en el eje x en el punto ( a , 0) y la directriz en la línea con la ecuación x = - a . En forma estándar la parábola siempre pasará por el origen.

Para una hipérbola rectangular o equilátera , una cuyas asíntotas son perpendiculares, existe una forma estándar alternativa en la que las asíntotas son los ejes de coordenadas y la línea x = y es el eje principal. Los focos entonces tienen coordenadas ( c , c ) y (- c , - c ) . ^[8]

• Círculo: x ² + y ² = a ²
• Elipse: x ²/a ² + y ²/b ² = 1
• Parábola: y ² = 4 hacha con a > 0
• Hipérbola: x ²/a ² - y ²/b ² = 1
• Hipérbola rectangular: ^[9] xy = c ²/2

Los primeros cuatro de estas formas son simétricas alrededor de tanto la x eje x y y eje x (por el círculo, elipse y la hipérbola), o acerca de la x eje x solamente (para la parábola). Sin embargo, la hipérbola rectangular es, en cambio, simétrica con respecto a las líneas y = x y y = - x .

Estas formas estándar se pueden escribir paramétricamente como,

• Círculo : ( un cos θ , un pecado θ ) ,
• Elipse : ( a cos θ , b pecado θ ) ,
• Parábola : ( en ² , 2 en ) ,
• Hipérbola : ( a sec θ , b tan θ ) o (± a cosh u , b sinh u ) ,
• Hipérbola rectangular : $${\ displaystyle (dt, {\ frac {d} {t}})} dónde $${\ displaystyle d = {\ frac {c} {\ sqrt {2}}}.}

Forma cartesiana general

En el sistema de coordenadas cartesiano , la gráfica de una ecuación cuadrática en dos variables es siempre una sección cónica (aunque puede estar degenerada ^[10] ), y todas las secciones cónicas surgen de esta manera. La ecuación más general es de la forma ^[11]

$${\ displaystyle Axe ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0,}

con todos los coeficientes números reales y A, B, C no todos cero.

Notación matricial

Artículo principal: Representación matricial de secciones cónicas.

La ecuación anterior se puede escribir en notación matricial como ^[12]

{\ displaystyle \ left ({\ begin {matrix} x & y \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \ end {matrix}} \ right) + \ left ({\ begin {matrix} D&E \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \ end {matriz}} \ derecha) + F = 0.}

La ecuación general también se puede escribir como

{\ displaystyle \ left ({\ begin {matrix} x & y & 1 \ end {matrix}} \ right) \ left ({\ begin {matrix} A & B / 2 & D / 2 \\ B / 2 & C & E & 2 /\ D / 2 & E / 2 & F \ end {matrix}} \ right) \ left ({\ begin {matrix} x \\ y \\ 1 \ end {matrix}} \ right) = 0.}

Esta forma es una especialización de la forma homogénea utilizada en la configuración más general de la geometría proyectiva (ver más abajo ).

Discriminante

Las secciones cónicas descritas por esta ecuación se pueden clasificar en términos del valor $${\ displaystyle B ^ {2} -4AC}, llamado el discriminante de la ecuación. ^[13] Por lo tanto, el discriminante es - 4Δ donde Δ es el determinante de la matriz{\ displaystyle \ left | {\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right |.}

Si la cónica no es degenerada , entonces: ^[14]

• si B ² - 4 AC <0 font=""> , la ecuación representa una elipse ;
  • si A = C y B = 0 , la ecuación representa un círculo , que es un caso especial de una elipse;
• si B ² - 4 AC = 0 , la ecuación representa una parábola ;
• si B ² - 4 AC > 0 , la ecuación representa una hipérbola ;
  • si A + C = 0 , la ecuación representa una hipérbola rectangular .

En la notación utilizada aquí, A y B son coeficientes del polinomio, en contraste con algunas fuentes que denotan los semiejes mayor y menor como A y B .

Invariantes

El discriminante B ² - 4 AC de la ecuación cuadrática de la sección cónica (o equivalentemente el determinante AC - B ² /4 de la matriz 2 x 2) y la cantidad A + C (la traza de la matriz de 2 x 2) son invariantes bajo Rotaciones arbitrarias y traslaciones de los ejes de coordenadas, ^{[14] [15] [16]} como es el determinante de la matriz 3 × 3 anterior . ^{[17] : pp. 60–62} El término constante F y la suma D ² + E ²Son invariantes solo bajo rotación. ^{[17] : pp. 60–62}

La excentricidad en términos de coeficientes.

Cuando la sección cónica se escribe algebraicamente como

$${\ displaystyle Axe ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0, \,}

La excentricidad se puede escribir en función de los coeficientes de la ecuación cuadrática. ^[18] Si 4 AC = B ^2, la cónica es una parábola y su excentricidad es igual a 1 (siempre que no sea degenerada). De lo contrario, suponiendo que la ecuación representa una hipérbola o una elipse no degenerada, la excentricidad viene dada por

$${\ displaystyle e = {\ sqrt {\ frac {2 {\ sqrt {(AC) ^ {2} + B ^ {2}}}} {\ eta (A + C) + {\ sqrt {(AC) ^ {2} + B ^ {2}}}}}},}

donde η = 1 si el determinante de la matriz 3 × 3 anterior es negativo y η = −1 si ese determinante es positivo.

También se puede mostrar ^{[17] : p. 89} que la excentricidad es una solución positiva de la ecuación.

$${\ displaystyle \ Delta e ^ {4} + [(A + C) ^ {2} -4 \ Delta] e ^ {2} - [(A + C) ^ {2} -4 \ Delta] = 0, }

donde otra vez $${\ displaystyle \ Delta = AC - {\ frac {B ^ {2}} {4}}.} Esto tiene precisamente una solución positiva, la excentricidad, en el caso de una parábola o elipse, mientras que en el caso de una hipérbola tiene dos soluciones positivas, una de las cuales es la excentricidad.

Conversión a forma canónica.

Ver también: Elipse § Forma canónica.

En el caso de una elipse o hipérbola, la ecuación

$${\ displaystyle Axe ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0 \,}

Se puede convertir a forma canónica en variables transformadas. $${\ displaystyle x ', y'}como ^[19]

$${\ displaystyle {\ frac {x '^ {2}} {- S / (\ lambda _ {1} ^ {2} \ lambda _ {2})}} + {\ frac {y' ^ {2}} {-S / (\ lambda _ {1} \ lambda _ {2} ^ {2})}} = 1,}

o equivalente

$${\ displaystyle {\ frac {x '^ {2}} {- S / (\ lambda _ {1} \ Delta)}} + {\ frac {y' ^ {2}} {- S / (\ lambda _ {2} \ Delta)}} = 1,}

dónde $${\ displaystyle \ lambda _ {1}} y $${\ displaystyle \ lambda _ {2}}Son los valores propios de la matriz.{\ displaystyle \ left ({\ begin {matrix} A & B / 2 \\ B / 2 & C \ end {matrix}} \ right)} - Es decir, las soluciones de la ecuación.

$${\ displaystyle \ lambda ^ {2} - (A + C) \ lambda + (AC- (B / 2) ^ {2}) = 0}

- y $${\ displaystyle S}es el determinante de la matriz 3 × 3 anterior , y$${\ displaystyle \ Delta = \ lambda _ {1} \ lambda _ {2}}Es nuevamente el determinante de la matriz 2 × 2. En el caso de una elipse, los cuadrados de los dos semiejes están dados por los denominadores en forma canónica.

Coordenadas polares

Desarrollo de la sección cónica como la excentricidad e incrementos

En coordenadas polares , la ecuación da una sección cónica con un foco en el origen y, si existe, la otra en un valor negativo (para una elipse) o un valor positivo (para una hipérbola) en el eje x.

$${\ displaystyle r = {\ frac {l} {1 + e \ cos \ theta}},}

donde e es la excentricidad y l es el semitransparente recto.

Como anteriormente, para e = 0 , la gráfica es un círculo, para 0 < e <1 font=""> la gráfica es una elipse, para e = 1 una parábola, y para e > 1 una hipérbola.

La forma polar de la ecuación de una cónica se usa a menudo en la dinámica ; por ejemplo, determinando las órbitas de los objetos que giran alrededor del Sol. ^[20]

Propiedades

Así como dos puntos (distintos) determinan una línea, cinco puntos determinan una cónica . Formalmente, dados cinco puntos en el plano en una posición lineal general , es decir, no hay tres colineales , hay un paso cónico único a través de ellos, que no será degenerado; Esto es cierto tanto en el plano euclidiano como en su extensión, el plano proyectivo real. De hecho, dados cinco puntos, hay una cónica que pasa a través de ellos, pero si tres de los puntos son colineales, la cónica será degenerada (reducible, porque contiene una línea), y puede que no sea única; ver más discusión .

Cuatro puntos en el plano en posición lineal general determinan una cónica única que pasa por los primeros tres puntos y tiene el cuarto punto como su centro. Por lo tanto, conocer el centro es equivalente a conocer dos puntos en la cónica con el fin de determinar la curva. ^[21]

Además, una cónica está determinada por cualquier combinación de k puntos en la posición general por la que pasa y 5 - k líneas que son tangentes a ella, para 0≤ k ≤5. ^[22]

Cualquier punto en el plano está en cero, una o dos líneas tangentes de una cónica. Un punto en una sola línea tangente está en la cónica. Se dice que un punto en una línea no tangente es un punto interior (o punto interior ) de la cónica, mientras que un punto en dos líneas tangentes es un punto exterior (o punto exterior ).

Todas las secciones cónicas comparten una propiedad de reflexión que se puede afirmar como: Todos los espejos con la forma de una sección cónica no degenerada reflejan la luz que viene desde o hacia un enfoque hacia o desde el otro enfoque. En el caso de la parábola, el segundo foco debe considerarse infinitamente lejano, de modo que los rayos de luz que se dirigen hacia el segundo foco o que vienen del mismo son paralelos. ^[23] [24]

El teorema de Pascal se refiere a la colinealidad de tres puntos que se construyen a partir de un conjunto de seis puntos en cualquier cónica no degenerada. El teorema también se aplica a las cónicas degeneradas que consisten en dos líneas, pero en ese caso se conoce como el teorema de Pappus .

Las secciones cónicas no degeneradas son siempre " lisas ". Esto es importante para muchas aplicaciones, como la aerodinámica, donde se requiere una superficie lisa para asegurar el flujo laminar y evitar la turbulencia .